信源数未知情况下基于嵌套阵列的DOA估计算法

沈志博，董春曦，黄 龙，赵国庆

（西安电子科技大学电子信息攻防对抗与仿真技术教育部重点实验室，陕西 西安710071）

0 引言

信号的波达方向（DOA）是电子侦察中需要获取的一个重要参数［1-2］，也是信号分选、辐射源识别以及定位跟踪的重要依据［3］。与雷达信号的DOA 估计不同，电子侦察中的DOA 估计没有信号的先验信息，并且日益复杂的电磁环境也对现有的DOA 估计方法提出了新的挑战［4］。传统的测向方法如最大信号法、比幅法等原理简单、易于实现，但是精度低、分辨力较差［5-6］，而干涉仪测向法虽然精度较高，但是现代电子对抗环境中辐射源数量多、分布密度大，同时多信号问题严重影响了其性能［7］。子空间分解算法，如MUISC算 法［8］、ESPRIT 算 法［9］以 及 其 推 广 和 改 进 算 法 由 于其超分辨能力以及良好的估计精度而得到了广泛的应用，但是这类方法是以预知信源的数量等先验信息为前提的，不正确的信源数估计将可能导致算法的失效，而且有效的阵列孔径也限制其能够同时处理的信源个数，因此应用到电子侦察系统中具有一定的局限性。文献［10］提出的嵌套阵列和文献［11］的互质阵列虽然有效地扩展了阵列孔径，但是仍需要较多的信号先验信息；文献［12］提出了一种未知信源个数的DOA 估计方法，阵列孔径损失较大，当信源数较多时，需要阵元数也较多，不易在电子侦察系统中工程实现。

针对上述问题，本文提出了一种基于2级嵌套阵列的DOA 估计方法。首先将协方差矩阵向量化作为新的阵列接收数据，并构造新的协方差矩阵；然后对新的协方差矩阵的每一行构造Toeplitz矩阵，并利用其联合对角结构生成代价函数；最后通过一维搜索求解出各信源的DOA。该方法能够在信源数量未知的情况下进行高精度的DOA 估计，并且有效地扩展了阵列孔径，节省了阵元的数量。

1 阵列模型

2级嵌套阵列结构如图1所示，阵元数为N 。其中第一级阵元数为N1，阵元间距为d1；第二级阵元数为N2，阵元间距为d2，且满足d2＝（N1＋1）d1，则第一级阵列阵元位置为｛n1d1，n1＝0，1，…，N1-1｝；第二级阵列阵元位置为｛n2d2-d1，n2＝1，2，…，N2｝。

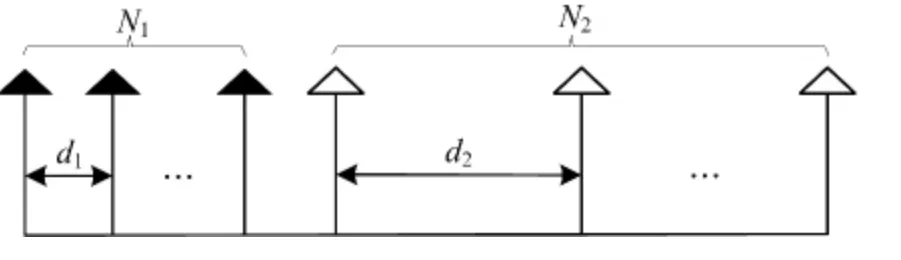
图1 2级嵌套阵列结构

假设空间中有K个不相关的窄带远场信号分别以方向角θk（k＝1，2，…，K）入射到阵列上，且满足θk∈（-90°，90°），d1≤λmin／2，λmin为最小信号波长。因此第k个信源的导向矢量可以表示为：

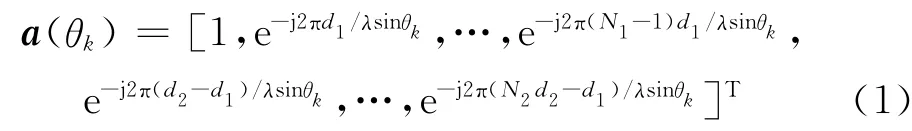
则相应的阵列流形为：

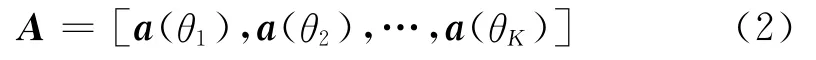
进而得到t时刻的阵列接收数据x（t）为：

式中，s（t）＝［s1（t），s2（t），…，sK（t）］为K×1 维向量；A 为N×K 维矩阵；n（t）为N×1维高斯白噪声。

2 算法原理

2.1 阵列孔径扩展

按照式（3）给出的阵列模型得到T（T ＝M×L）次快拍数据，并将其分为M 段，每段的数据长度为L。假设各信源每段的数据满足近似平稳条件，即：

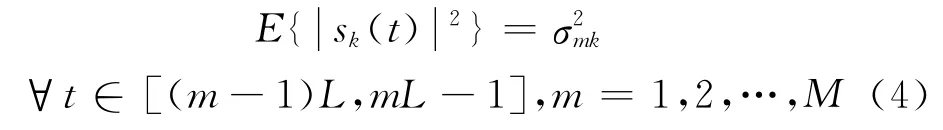
则第m 段数据的协方差矩阵为：

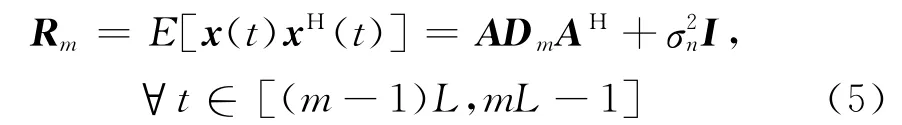
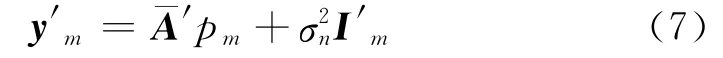
进而得到新的阵列接收数据：

式中，Y ＝［y′1，y′2，…，y′M］为2 Ni×M 维阵列接收数据矩阵，P ＝［p1，p2，…，pM］为K×M 维信号矩阵，E ＝［I′1，I′2，…，I′M］为2 Ni×M 维噪声矩阵。

2.2 信源数未知情况下DOA估计

利用式（9）得到的新的阵列接收数据在信源数未知的情况下进行DOA 估计。首先计算新的阵列接收数据的协方差矩阵：

对协方差矩阵的第n 行进行Toeplitz变换，生成Toeplitz矩阵：

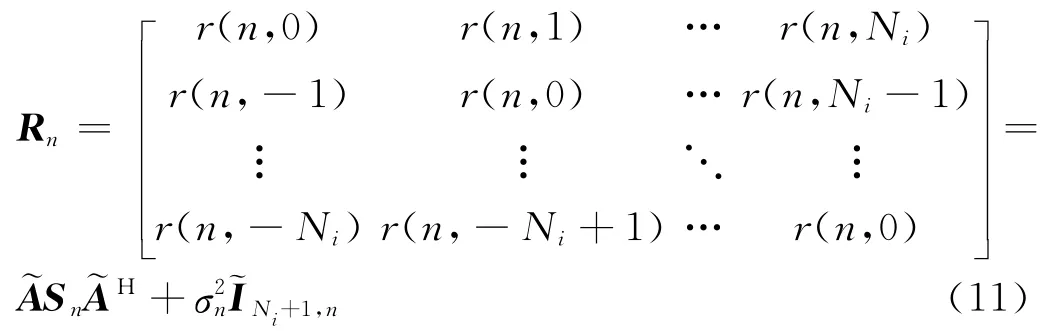
根据文献［15～16］推导，可得最终的空间谱估计表达式为：

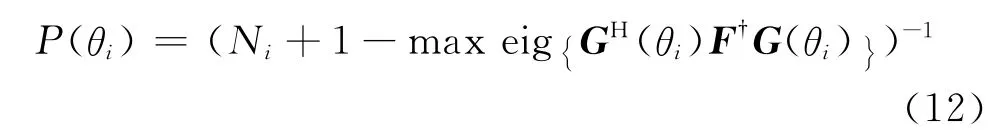
其中：

式中，max eig｛·｝表示矩阵的最大特征值。可以看出，算法是通过一维搜索的方式确定谱峰的位置，Ns为搜索次数；且只需要求取最大特征值即可，故不需要知道确切的信源个数就可以得到所有信号的DOA估计。

3 算法分析

经过上述分析可以得出算法的基本步骤如下：

1）将T 次快拍数据分为M 段，每段长度为L，分别计算协方差矩阵Rm，m ＝1，2，…，M ；

2）向量化协方差矩阵，并去掉冗余的元素，形成新的阵列接收数据y′m，m ＝1，2，…，M ；

3）计算y′m的协方差矩阵；

4）选取R 中的前Ni＋1 行，对每个行向量进行Toeplitz变换，构造Toeplitz矩阵；

5）利用式（13）和式（14）构造矩阵F 和G（θ）；

6）利用式（12）进行谱峰搜索，确定谱峰的位置，进而得到各信源的DOA 估计。

该算法的运算包括阵列扩展前后的协方差矩阵的计算以及矩阵F 和G（θ）的构造，因此其计算量约为该算法不需要预知信源的个数，并且能够在欠定的条件下进行有效的估计，即能够同时估计的信源个数大于实际的阵元数。文献［12］的算法中虽然不需要预知信源数，但是N个阵元最多只能估计（N ＋1）／2个信源，而本文提出的算法利用嵌套阵列有效地扩展了阵列孔径，因此，N个阵元最多能够估计的信源个数为：

阵列孔径扩展后，角度分辨能力和估计精度也得到了相应的提高，与文献［12］中的算法相比，该算法具有更高的估计精度和分辨力。另外，该算法进行谱峰搜索时选取的是最大特征值，因此对于噪声具有一定的鲁棒性，在低信噪比的情况下也能够进行正确的估计。

4 仿真分析

本节通过仿真实验对本文所提出的算法进行分析与验证。选用角度均方根误差（RMSE）来描述算法的估计性能，其定义为：

1）仿真实验1

假设阵元数N ＝5，采用2级嵌套结构，即N1＝2，N2＝3。快拍数T＝8192，数据分为16段（M ＝16），每段长度L ＝512。4个信源分别以到达角-15°、5°、30°和45°入射到阵列上，信噪比为15dB。图2分别给出文献［12］算法（虚线）和本文算法（实线）的DOA 估计结果。

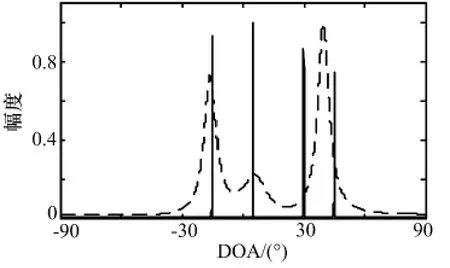
图2 DOA 估计结果（信源数K＝4）

从图2的结果中可以看出，在5个阵元的情况下，文献［12］中的算法只能估计出3个信源，而本文算法能够对4个信源进行正确的估计。由于算法进行了阵列孔径扩展，增加了自由度，因此能够在欠定的情况下（信源数大于实际阵元数）进行DOA 估计。

为了进一步验证算法能够估计的信源数量，选取8个信源，到达角分别为-55°、-35°、-20°、-5°、5°、20°、30°和45°。图3给出了信源数K ＝8时的估计结果。

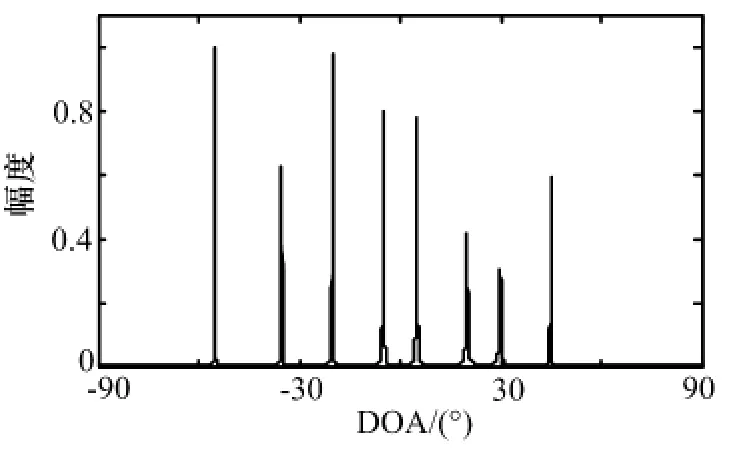
图3 DOA 估计结果（信源数K＝8）

根据公式（15）所示，5个阵元最多可以估计的信源数为（52-1）／4＋（5-1）／2＝8。而从图3的结果可以看出，算法能够对全部8个信源的DOA 进行正确的估计，与理论分析结果一致，从而验证了算法的正确性。

2）仿真实验2

针对算法的估计精度进行实验，选取3个信源，到达角分别为-15°、5°和30°，令信噪比SNR 从-5dB变化到20dB，其它实验条件与仿真实验1相同。每个信噪比下进行500次蒙特卡罗实验，并对文献［12］和本文算法的均方根误差与信噪比的关系曲线分别进行描绘，仿真结果如图4所示。

图4 不同信噪比下的估计均方误差比较

文献［12］算法在SNR低于2.5dB时已无法正确估计3个信源，因此图中未标出。从图4可以看出，在阵元数N 相同的条件下，本文算法具有更高的估计精度。

为了进一步验证算法的DOA 估计精度，图5 给出了不同信噪比下的估计均方误差与克拉美罗界（CRB）［17］进行比较的结果，其中CRB（N）表示阵元数为N 的克拉美罗界。

不同信噪比下的的估计均方误差与CRB比较

从图5 的仿真结果可以看出，算法的DOA 估计均方误差随信噪比变化曲线在CRB（5）和CRB（17）之间。由于算法进行了阵列孔径扩展，N个阵元扩展后形成一个（N2-1）／2＋N 的虚拟均匀线阵，因此算法的估计精度要优于5个阵元的线阵，而低于17个阵元的线阵的估计精度。

3）仿真实验3

针对算法分辨力进行实验，选取2个到达角度相近的信源（15°和16°），阵元数N ＝9，其它实验条件与仿真实验1相同，文献［12］算法（虚线）和本文算法（实线）的DOA 估计结果如图6所示。

图6 DOA 分辨力比较

从图6的仿真结果可以看出，当2个信源角度相近时，文献［12］算法已经无法区分，而本文算法仍然能够正确地估计出2个信源的角度，分辨能力更优。由于算法进行了阵列扩展，有效孔径变大，因此具有更高的DOA 分辨力。

5 结束语

辐射源的DOA 估计在电子侦察中有着重要的研究意义。本文针对信源数未知情况下的DOA 估计问题，提出了一种基于2级嵌套阵列的DOA 估计算法。理论分析和仿真实验表明，该方法扩展了阵列孔径，能够利用较少的阵元个数同时估计多个信源的DOA，并且具有较高的估计精度和分辨力，对信噪比要求也不高。因此，该算法能够满足当前电子侦察测向系统的要求。■

［1］Dai JS，Xu X，Zhao D，et al.Direction-of-arrival estimation via real-valued sparse representation［J］.IEEE Antennas and Wireless Propagation Letters，2013，12：376-379.

［2］蔡晶晶，李鹏，赵国庆，等.RD-MUSIC的二维DOA 估计方法［J］.西安电子科技大学学报，2013，40（3）：81-86.

［3］赵国庆.雷达对抗原理［M］.西安：西安电子科技大学出版社，1999.

［4］Richard WG.电子情报（ELIENT）雷达信号截获与分析［M］.北京：电子工业出版社，2008.

［5］翟庆伟，王玉，宫兵.波束比幅法测向技术研究［J］.无线电通信技术，2007，33（6）：55-56.

［6］陶海红，夏南，王楠.单比特宽带数字接收机的频域多波束测向技术［J］.电波科学学报，2009，24（1）：83-89，110.

［7］李淳，廖桂生，李艳斌.改进的相关干涉仪侧向处理方法［J］.西安电子科技大学学报（自然科学版），2006，33（3）：400-403.

［8］Schmidt RO.Multiple emitter location and signal parameter estimation［J］.IEEE Trans on Antennas Propag，1986，34（3）：276-286.

［9］RoyR，Paulraj A，Kailath T.ESPRIT-A subspace rotation approach to estimation of parameter of cisoids in noise［J］.IEEE Trans.on Acoustics，Speech and Signal Processing，1986，34（5）：1340-1342.

［10］Pal P，Vaidyanathan P.Nested arrays：A novel approach to array processing with enhanced degrees of freedom［J］.IEEE Trans.on Signal Process.，2010，58（8）：4167-4181.

［11］Vaidyanathan P，Pal P.Sparse sensing with co-prime samplers and arrays［J］.IEEE Trans.on Signal Process.，2011，59（2）：573-586.

［12］Qian C，Huang L，Zeng WJ，et al.Direction-of-arrival es-timation for coherent signals without knowledge of source number［J］.IEEE Sensors Journal，2014，14（9）：3267-3273.

［13］Ma WK，Hsieh TH，Chi CY.DOA estimation of quasistationary signals with less sensors than sources and unknown spatial noise covariance：A Khatri-Rao subspace approach［J］.IEEE Trans.on Signal Process.2010，58（4）：2168-2180.

［14］Han KY，Nehorai A.Nested vector-sensor array processing via tensor modeling［J］.IEEE Trans.on Signal Process，2014，62（10）：2542-2553.

［15］HanFM，Zhang XD.An ESPRIT-like algorithm for coherent DOA estimation［J］.IEEE Antennas and Wireless Propagation Letters，2005，4：443-446.

［16］ZengWJ，Li XL，Zhang XD，et al.Direction-of-arrival estimation based on the joint diagonalization structure of multiple fourth-order cumulant matrices［J］.IEEE Signal Processing Letters，2009，16（3）：164-167.

［17］王永良，等.空间谱估计理论与算法［M］.北京：清华大学出版社，2004.