基于二阶锥优化的复系数FIR滤波器设计
2015-12-21王铁丹陈昌云
王铁丹,郭 辉,张 昕,陈昌云,高 祺
(中国航天科工集团8511研究所,江苏 南京210007)
0 引言
FIR滤波器因其良好的频率响应及线性相位特性而被广泛应用到大量工程场合,而随着需求的不断扩大,在波形均衡器、地震杂波滤波及卫星信道分配等应用领域,要求设计出具有任意幅度及相位响应的复系数滤波器。基于实系数交错定理首先被推广到了复数域,从而提高复系数滤波器的一些性能要求[1]。之后,文献[2~3]使用最小二乘法方设计具有低群延时的复系数滤波器。周青松[4]等将二阶锥优化引入低群延时复系数FIR 滤波器设计,取得较好效果。因此,本文利用二阶锥优化(SOCP)方法来设计具有任意幅相响应的复系数FIR 滤波器,通过少许频率响应期望点进行内插,再通过MATLAB 的CVX 工具箱,简单有效地设计出期望的复系数FIR 滤波器,在工程中得到良好的应用。
采用FIR 滤波器对具有一定带宽的信号进行幅相均衡,减少微波器件带来的信号失真,其系统框图如图1所示。

图1 基于FIR 滤波器的幅相均衡器系统框图
当经过正交解调的数字复信号数据进入设计好的FIR 滤波器后,该滤波器的幅频及相频响应在期望频率段内都是和频率相关的函数,达到对信号进行幅相均衡的效果,而该方法和核心问题为在已知预设频谱响应的情况下如何设计出合适的FIR 滤波器系数。
1 FIR滤波器设计算法
1.1 二阶锥优化的基本原理
二阶锥优化是凸优化问题的一个子集。二阶锥优化是在满足一组二阶锥优化和线性等式约束的条件下使某线性函数最小化,它具有成熟性高,计算结果精确等优点[5]。
二阶锥优化一般形式为:

式中,y∈Cα×1为优化向量,b∈Cα×1,Ai∈Cαi()-1×α,bi∈Cαi( )-1×1,ci∈Cα×1,di∈R,F∈Cg×α,g∈Cα×1,表示Euclid范数,此处为l1范数,C 表示复数集,R 表示实数集。
其中每个约束可写成二阶锥形式:


式(1)中的Fy=g 可以表示为零锥的形式[5]:


由上述推导可知,线性规划和凸二次规划都是二阶锥规划的特例。将非负集合表示为R+,则二阶锥问题都可以表述为:
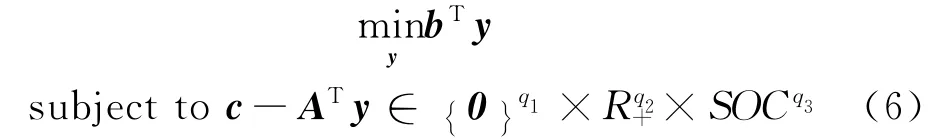
式中的约束表示有q1个等式约束,q2个线性不等式约束及q3个二阶锥优化。
1.2 滤波器系数计算
假设FIR 滤波器的冲击响应为:

其在频率fk上的频率响应为:

工程中一般对频段进行等间隔划分后确定部分特殊频点的幅相响应,为了使滤波器设计更平滑,对特殊频点进行内插,一般测量10~20个特殊频点后,内插至1000~2000个期望响应值。期望滤波器响应可表示 为:Hidea= [Hidea(f1),Hidea(f2),…,Hidea(fK)]。而实际设计滤波器响应为: Hdesign=[Hdesign(f1),Hdesign(f2),…,Hdesign(fK)]。则期望滤波器与设计滤波器响应的误差可以表示为:

p 的不同取值可以代表不同的约束形式,当p 取值为1,表示L1范数,其定义为:

常用的还有当p 取值为2,表示L2范数,当p 为inf时,表示无穷范数,其定义分别为:

当使用无穷范数时,滤波器设计法则即为经典的切比雪夫逼近理论设计法。ε表示了设计的滤波器与期望响应之间在通带内的误差,而在非通带范围,幅相均衡器要求不对带外信号进行放大即可,即:

式中,fm为对需要均衡的带外频率的均匀划分。整个约束可以表示为:

式(14)通过使用MATLAB 中的CVX 工具箱可对二阶锥优化进行求解。CVX 工具箱由斯坦福大学的Michael Grant及Stephen Boyd制作,用于求解线性优化(Linear Programs)、二次优化(Quadratic Programs)、二阶锥优化和半定优化(Semidefinite Programs)。
2 设计实例
大量工程项目中遇到需要通过FIR 滤波器设计幅相均衡器达到通道均衡等目的,该算法负责计算所需的复系数滤波器系数,计算的结果可直接应用于各类FPGA 或者DSP系统中。下面通过设计实例来证明本文所提算法的有效性。
1)工程实例一
该工程中要求设计一幅频均衡器,幅度校正系数为:g=[-8.75-7.78-6.72-6.86-6.80-4.98-2.42-1.42 0.00],对应角频率为0.1π~0.9π,等间隔取样共11个点,校正结果如图2所示。
通过图2的左图可以看到实际设计的幅频校正曲线与理想的幅频校正曲线非常接近,通过计算得到的8阶复系数FIR 滤波器校正后,幅度抖动由原来的8dB 降低到0.7dB校正效果明显。由于该实例未对相频校正提出要求,设计的相频曲线为线性相位。
2)工程实例二
该工程要求设计一幅相频均衡器,幅度及相位校正曲线分别如图3及图4所示。
可以看到经过复系数FIR 均衡器校正后,幅度偏差由原来的最大-5.5dB 降低为0.31dB,相位扰动也由原来的最大偏差40°降低为2.5°,校正效果明显。
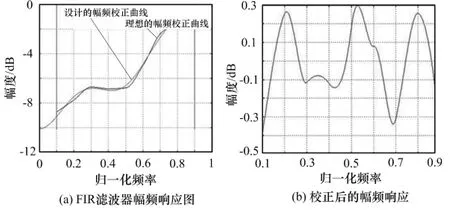
图2 8阶实系数滤波器校正结果,校正后幅度差值为0.7dB

图3 32阶FIR 滤波器幅频校正图,校正后幅度差值为0.3115dB

图4 32阶FIR 滤波器相频校正图,校正后相位最大差值2.5343°
3 结束语
FIR滤波器可以一定带宽信号进行幅度及相位上一致性的校正。低阶数的实系数FIR滤波器即可对幅频误差校正取得较好的效果,需要的硬件资源很少。而需要进行幅频及幅相同时校正的情况,需设计复系数FIR 滤波器,需要的阶数一般也高于单纯进行幅频校正的滤波器。■
[1]Karam LJ,Mcclellan JH.Complex Chebyshev approximation for FIR filter design[J].IEEE Transactions on Circuits and Systems II,1995,42(3):207-246.
[2]赖晓平,袁博,徐东.低群延迟有限冲激响应滤波器约束最小二乘设计[J].浙江大学学报(工学版),2010,44:1271-1275.
[3]张少蔚,徐东,袁博,等.复数FIR 滤波器椭圆误差约束最小二乘设计[J].浙江大学学报(工学版),2010,44:1339-1342.
[4]周青松,张剑云,李小波,等.二阶锥规划方法对于低群延时复系数有限冲激响应数字滤波器优化设计[J].电路与系统学报,2011,16(3):75-80.
[5]Lobo MS,Vandenberghe L,Boyd S.Applications of second order cone programming international linear algebra society symposim on fast algorithms for control[J].Signals and Image Processing,1998,284:193-228.
