基于动能原理的能量式回弹仪检测混凝土抗压强度研究

王大勇，马祥君

（1.廊坊市建设工程质量检测中心，河北 廊坊 065000；2. 廊坊市阳光建设工程质量检测有限公司，河北 廊坊 065000）

基于动能原理的能量式回弹仪检测混凝土抗压强度研究

王大勇1,2，马祥君2

（1.廊坊市建设工程质量检测中心，河北 廊坊 065000；2. 廊坊市阳光建设工程质量检测有限公司，河北 廊坊 065000）

本文介绍了一种用于结构混凝土抗压强度检测的新型能量式回弹仪，阐述了该类回弹仪与普通回弹仪工作原理的差异。根据试验数据，给出了两类回弹仪在水平向检测混凝土浇筑侧面工况下的回弹值间的转换算式，同时建立了采用能量式回弹仪检测混凝土浇筑侧面与底面的混凝土测强曲线，最后对能量式回弹仪检测混凝土浇筑底面的回弹值及与之对应的混凝土侧面回弹值间的关系进行回归拟合，给出混凝土浇筑面修正公式。研究结果可供工程质量检测与控制参考。

能量式回弹仪；混凝土抗压强度；测强曲线；换算公式

0　引言

目前对于工程现场结构混凝土抗压强度推定常采用回弹法[1]，因此普通回弹仪（R 值回弹仪）得到了广泛的推广与应用，但在使用过程中存在诸如：非水平方向回弹时需要对检测值进行角度修正，而角度修正往往会传递测试误差；常规保养间隔时间短、机械系统的维护技术要求高以及保养不到位，容易造成滑块、轨道等部位摩擦力变化而影响检测结果准确性等问题，从而对检测结果造成很大的影响。能量式回弹仪（Q 值回弹仪）是一种新型回弹仪，它是通过光电子技术测定回弹系数，即 Q 值，其物理意义是弹击杆弹击受检混凝土前后瞬间的弹击能量的动能比值，它与弹击杆弹击后的位移变化无关，因此，指针中心导杆的摩擦力，牵引指针运动的反弹力以及装置和样本间的相对速度对 Q 值影响较小；非水平方向的回弹测试 Q 值不考虑弹击锤的重力影响，因而无需进行角度修正。

由于 Q 值回弹仪与 R 值回弹仪检测混凝土抗压强度的工作原理不同，二者之间不存在严格的数学对应关系，因此不适用于现行行业标准 JGJ/T 23—2011《回弹法检测混凝土抗压强度技术规程》，应另行建立测强曲线后，借以推定结构混凝土抗压强度。本研究对比两种回弹仪的工作原理，分析其测试结果的联系，同时采用本地区常用原材料配制试验用混凝土，按标准方法成型标准立方体试件与大型实体结构模型，建立能量式回弹仪检测混凝土抗压强度曲线，最后给出了能量式回弹仪检测混凝土浇筑底面与其相应侧面间的数值换算关系。研究结果可供结构混凝土强度检测与控制参考。

1　回弹仪工作原理

Q 值回弹仪的工作原理见式 (1)，水平向检测混凝土浇筑侧面时的R值回弹仪的工作原理见式 (2)。

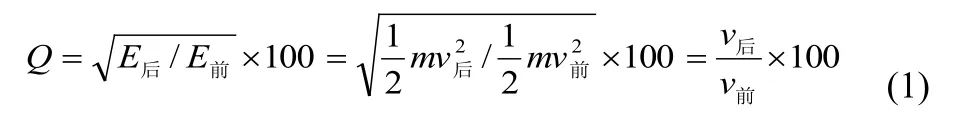
R 值回弹仪检测混凝土浇筑侧面时，非水平向与水平向回弹值间的理论关系可根据功能原理[2]，由以下两式：

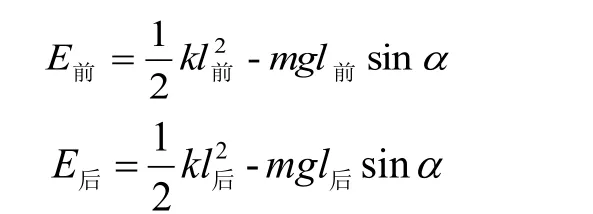
经理论推导，得到式（3）。

式中：

Q—— N 型能量回弹仪弹击混凝土浇筑侧面后的回弹值；

R0——普通回弹仪在水平向弹击混凝土浇筑侧面后的回弹值；

Rα——普通回弹仪在非水平向弹击混凝土浇筑侧面的回弹值；

m——回弹仪弹击锤的质量（115g）；

g——重力加速度（9.8N/kg）；

k——回弹仪弹击拉簧的弹性刚度（785.0N/m）；

v前——N 型能量回弹仪弹击前的瞬时速率；

v后——N 型能量回弹仪弹击后的瞬时回弹速率；

l前——普通回弹仪弹击前弹击拉簧的拉伸长度，75mm；

l后——普通回弹仪弹击后弹击拉簧的回弹长度；

α——普通回弹仪的弹击杆及其后盖所在的轴线与水平线的夹角。

δ——回弹仪本身的固有系数，其值可由 δ=2mg/kl 计算。

由式 (1) 可知，能量回弹仪测试值 Q 仅与其弹击前后的瞬时速率的比值有关，与弹击角度无关；由式 (2) 可知，普通回弹仪水平向测试值 R0仅与其弹击前的弹击拉簧长度及弹击后拉簧的回弹长度的比值有关；由式 (3) 可知，普通回弹仪非水平向测试值 Ra除与其弹击前的弹击拉簧长度及弹击后拉簧的回弹长度的比值有关外，还与回弹仪的弹击角度有关。

2　试验设计

2.1混凝土原材料及配合比

试验采用本地区常用原材料：42.5 级普通硅酸盐水泥；Ⅱ级粉煤灰；细骨料为保定河砂，中砂；粗骨料为卵石破碎的粒径 5～25mm 碎石；ZG-C 型泵送减水剂；拌合用水为当地自来水。

混凝土配合比设计 C20、C30、C40、C50 共四个强度等级，具体混凝土配合比如表 1 所示。

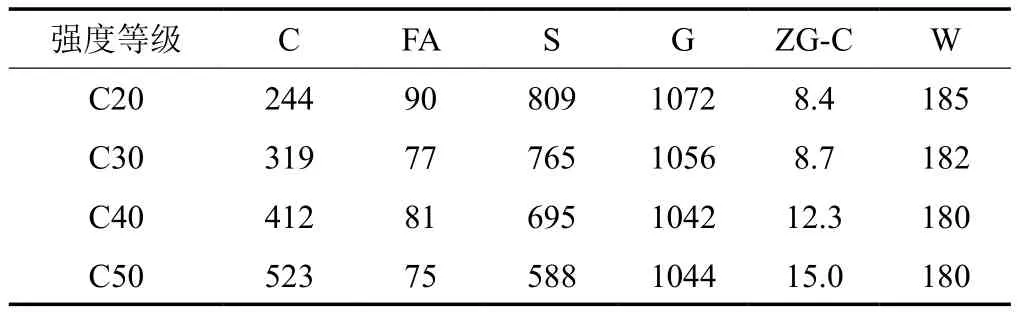
表1　试验混凝土配合比 kg/m3

2.2结构实体模型与标准立方体试件

委托生产质量稳定的大型商品混凝土公司提供试验混凝土并泵送浇筑成型四个大型结构实体模型与150mm×150mm×150mm 标准立方体试件，见图 1。混凝土结构实体模型浇筑成型并拆除模板后，按现行 GB 50204—2011《混凝土结构工程施工质量验收规范》养护 14d 昼夜，后自然养护，裸置备用；标准立方体试件移至室外阴凉处品字型码放备用。

2.3测试方法

在龄期 14d、28d、60d、90d、180d、360d 时，从每强度等级试件中随机抽取不少于 2 组立方体试件及在大型结构实体模型的混凝土墙体侧面与现浇楼板底面进行回弹测试及碳化深度测量，并对应回弹测区钻取直径 100mm 的标准芯样。对得到的同龄期混凝土试件在试验压力机下进行力学破型试验。试验用仪器设备均检定有效。

图1　大型结构实体模型

3　试验结果

3.1R 值与 Q 值的换算关系

文献 [3] 对 Q 值回弹仪与 R 值回弹仪在水平向弹击混凝土侧面工况的回弹值间的相关性进行了理论分析，得到了推导公式 (4)。现结合本文试验所得到的两种回弹仪的回弹值测试结果进行比较，结果见图 2。

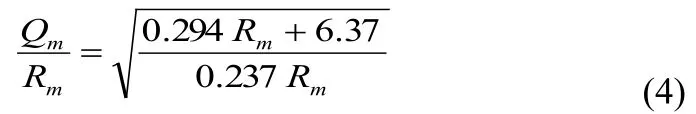
由图 2 可知，在 R 值为 30～55 范围内，有一部分试验数据散点落在推导公式 (4) 的曲线上下，但绝大部分数据位于推导公式回归线以下，表明理论推导计算公式与回弹仪的实际测试值间存在较大的差异。

图2　推导公式与试验数据的比较

由于目前国内，对 R 值回弹仪的应用较为广泛且有成熟适用的测强曲线，因此有必要结合试验数据，给出 R 值与 Q值的转换算式。基于试验数据，采用最小二乘法对有效试验数据进行拟合，得到的两种回弹仪水平向检测混凝土浇筑侧面的测区回弹值的均值间的换算公式，见式 (5)、(6)，二者的散点图见图 3。经统计，两式的相关系数依次为0.89、0.89，平均相对误差为±3.56%、±4.02%，相对标准差为4.58%、5.14%，计算结果与试验值吻合较好。

式中：

Qm,i——采用标称能量为 2.207J 的 N 型能量式回弹仪水平向检测混凝土浇筑侧面的第 i 测区回弹值的均值，精确到0.1；

Rm,i——采用标称能量为 2.207J 的普通回弹仪水平向检测混凝土浇筑侧面的第 i 测区回弹值的均值，精确到 0.1。

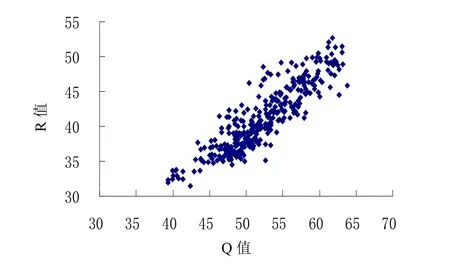
图3　水平向检测混凝土浇筑侧面R 值与 Q 值的散点图

3.2能量式回弹仪检测混凝土浇筑侧面测强曲线

立方体试件与墙体芯样试件试验共取得 408 组有效数据,混凝土试件抗压强度范围 29.1～85.3MPa，回归用数学模型采用复合幂指数数学模型。据最小二乘法原理，由 Excel 软件回归拟合，得到的测强曲线见式 (7) 与图 4。

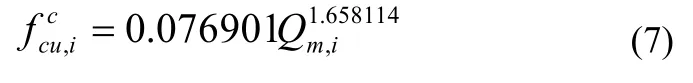
式中：

图4　混凝土抗压强度与其侧面 Q 值的关系

陕西省建筑科学研究院[3]经过试验研究，得到的能量式回弹仪的混凝土测强曲线见式 (8)，湖南大学对 C50～C100 高强混凝土进行龄期 7～60d 的回弹测试得到的幂函数测强曲线见式 (9)。本文式 (7)与全国各地能量式回弹仪测强曲线的比较见图 5。

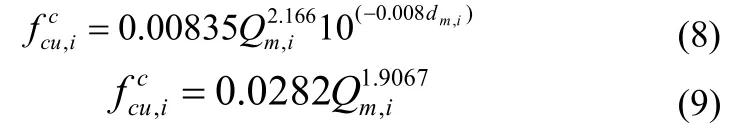
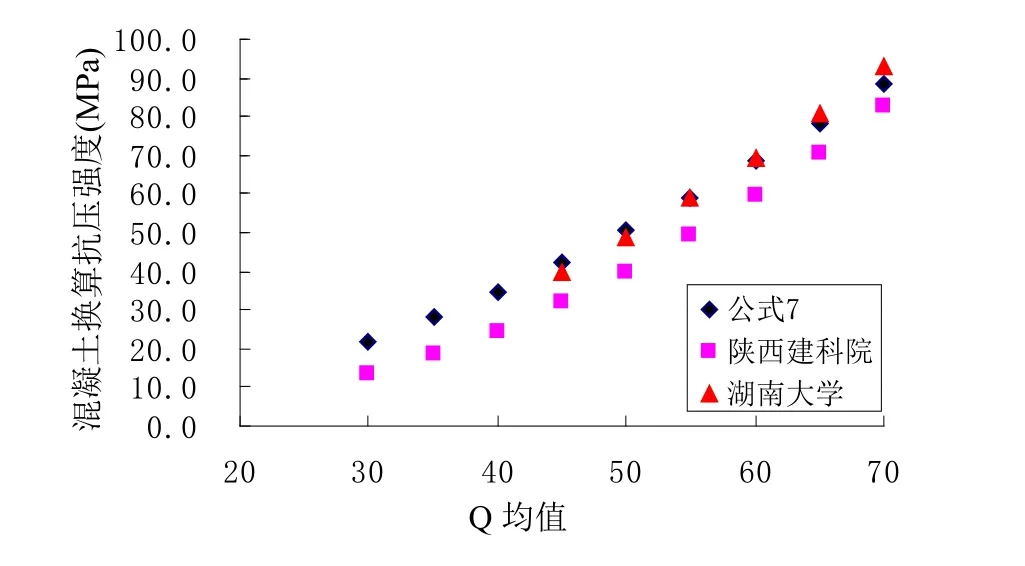
图5　本文测强曲线与各地测强曲线的比较

由图 5 可知，各测强曲线均表现出随 Q 值的增大，混凝土抗压强度增高；在相同 Q 值时，陕西省建筑科学研究院测强曲线换算强度偏低，本文曲线与湖南大学测强曲线换算强度相差不多，均明显高于前者。

3.3能量式回弹仪向上检测混凝土浇筑底面测强曲线

立方体试件与墙体芯样试件试验共取得 297 组有效数据,混凝土试件抗压强度范围 26.4～85.0MPa，回归用数学模型采用复合幂指数数学模型。据最小二乘法原理，由 Excel 软件回归拟合，得到的测强曲线见式 (10) 与图 6。

式 (10) 相关系数 r 为 0.71，平均相对误差 δ 为±13.6%,相对标准差 εr为16.0%，符合 JGJ/T 23—2011《回弹法检测混凝土抗压强度技术规程》所要求的平均相对误差 δ 不大于±14.0%，相对标准差 εr不大于 16.0% 的地区测强曲线的技术指标规定。

图6　混凝土抗压强度与其底面 Q 值的关系

3.4能量式回弹仪水平向检测混凝土浇筑底面及其相应侧面间Q 值的换算关系

图 7 为两种回弹仪采取水平向检测立方体试件底面 Q 值及其相应侧面 Q 值的散点图。采用最小二乘法由 Excel 软件回归拟合，得到能量回弹仪检测混凝土浇筑底面的修正公式见式 (11)。式 (11) 的相关系数 r 为 0.88，平均相对误差 δ 为±1.98% 相对标准差 εr为 2.08%，计算结果与试验值吻合较好。

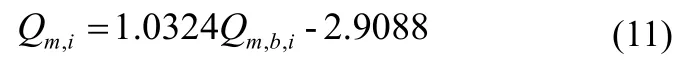
式中：

Qm,i——能量回弹仪水平向检测混凝土浇筑侧面的第 i 测区回弹值的均值，精确到 0.1；

Qm,b,i——能量回弹仪水平向检测混凝土浇筑底面的第 i测区回弹值的均值，精确到 0.1。

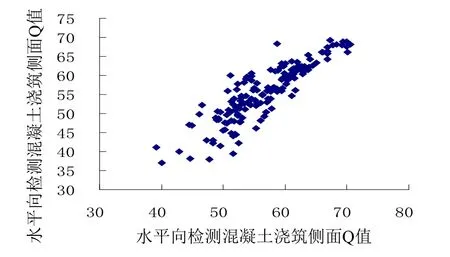
图7　立方体试件底面 Q 值及其相应侧面 Q 值的关系

4　结论

（1）对能量式回弹仪与普通回弹仪进行了比较，阐述其各自的工作原理，表明能量式回弹仪具有不受重力影响，能够进行任意角度测试而无需进行角度修正的特点，同时分析了 Q 值回弹仪较 R 值回弹仪在保养、维护及使用过程中的优越性。

（2）为解决能量式回弹仪与现行 JGJ/T 23—2011《回弹法检测混凝土抗压强度技术规程》的衔接问题，对两类回弹仪的回弹测试值间的关系进行了理论推导公式与实际回弹数值的比较与分析，给出了两类回弹仪间的回弹数值的转换算式。

（3）为提高检测的准确性，以立方体试件与大型实体结构混凝土试验模型为研究对象，采用能量式回弹仪检测混凝土抗压强度，根据最小二乘法原理，直接确定了 Q 值与混凝土抗压强度之间的数学关系式并分别给出了能量式回弹仪检测混凝土浇筑测面以及混凝土浇筑底面的测强曲线。通过误差分析，确定误差范围，进而确定了数学关系式的适用性，其为能量式回弹仪的广泛应用提供了可靠的试验依据。

（4）以立方体试件的混凝土浇筑侧面和底面为研究对象，采用能量式回弹仪分别测试其回弹值而得到试验数据，据最小二乘法原理得到了能量式回弹仪检测混凝土浇筑底面的修正公式，为今后对统一能量式回弹仪的测强曲线奠定了基础。本文研究结果可供能量式回弹仪检测结构混凝土抗压强度的理论分析研究和工程实际应用提供参考。

[1] JGJ/T 23—2011．回弹法检测混凝土抗压强度技术规程[S].

[2] 裘炽昌，朱金根．回弹法测强角度修正值的研究[J]．混凝土，1983(1): 11-13．

[3] 邓昌宁．能量式 Q 值回弹仪的应用研究[J]．北方交通，2013(12): 5-7．

[4] 文恒武．Q 系列回弹仪检测混凝土抗压强度试验研究[A]．第十一届全国建设工程无损检测技术学术会议论文集，2012: 206-210．

［通讯地址］河北省廊坊市龙河高新技术产业区夏荣道 10 号廊坊市阳光建设工程质量检测有限公司（065000）

Inspection of concrete compressive strength of energy rebound tester based on the principle of kinetic energy

Wang Dayong1,2, Ma Xiangjun2
( 1. Langfang Construction Engineering Quality Testing Center, Langfang 065000; 2. Langfang Yangguang Construction Engineering Quality Supervision Co., Ltd., Langfang 065000)

This paper proposes a method for the new energy rebound instrument testing compressive strength of structural concrete, it expounds the differences between the hammer and the principle of instrument work normal rebound. Based on the test data,the article gives the conversion between the two rebound hammer values to detect concrete pouring side under the condition of test at the level of the formula. At the same time, it was developed the strength measuring curves by using the energy rebound tester for the detection of concrete pouring the side surface and the bottom surface of the concrete. At last,the test of concrete test hammer bottom surface energy value of the regression relations and the corresponding concrete side test value of the correction formula is given, the pouring of concrete.The results can be reference for the engineering quality detection and control.

energy rebound instrument; concrete strength; strength curve; conversion formula

王大勇（1974—），男，教授级高级工程师，国家一级注册建造师，中国土木工程学会建设工程无损检测技术专业委员会委员，结构室主任，现从事工程质量检测鉴定与研究工作。