双向偏转平台消隙齿轮拉簧的优化设计
2018-11-06梁应选徐永帅魏碧辉
陈 纯, 陈 周, 梁应选, 徐永帅, 魏碧辉
(陕西理工大学 机械工程学院, 陕西 汉中 723000)
理论上齿轮啮合时无侧隙最好,而实际上由于制造、安装及温度等变化引起的尺寸误差,导致轮齿非工作面间产生齿侧间隙,在进给系统反向时就会产生空程误差。因此,需要在结构上采取措施来减小或消除此反向空程误差,满足传递所需的功率。调整中心距法、双片薄齿轮错齿消隙法和轴向调整法都是目前常用的方法[1-4]。其中双片薄齿轮错齿消隙法广泛应用于数控机床直齿圆柱齿轮的传动。
有学者对在一定范围内伸缩变化的普通拉簧进行了优化设计,例如杨宇强等[5]、曹坤等[6]都研究了基于MATLAB的拉簧优化设计,闫思江等[7]研究了基于Solidworks的圆柱拉簧的优化设计,虽然都是对拉簧进行优化设计,但由于消隙拉簧的伸缩变化仅局限于齿轮的齿侧间隙范围,拉簧行程十分微小,需要提供的力却较大,因此设计不同于一般的普通拉簧,所以在优化设计上也与一般拉簧的优化设计有所不同。
在双向偏转平台中,消隙齿轮中的拉簧既要保证传递平台所需的偏转力,消除反向空程误差,又不能增加齿面间的磨损,以保证传动效率,其外形尺寸也必须约束在消隙齿轮的几何参数范围内。本文利用极大极小值优化方法,以消隙拉簧轻量化为优化目标,以驱动电机的输出扭矩、消隙齿轮的结构参数等为约束条件,对消隙齿轮中的拉簧进行优化设计,并将优化结果换算成消隙拉簧的工作参数。
1 双向偏转平台简介
双向偏转平台如图1所示,平台台面用销轴与呈正十字空间交错的内、外齿轮拱连接,外齿轮拱由置于底座上的驱动电机和其轴上的消隙齿轮驱动,由联结于底座和外齿轮拱上的外圆弧导轨副导向,完成一个绕特定轴(定义为X轴)方向的偏转;内齿轮拱由联结于外齿轮拱上的驱动电机和其轴上的消隙齿轮驱动,由联结于外齿轮拱和内齿轮拱上的内圆弧导轨副导向,完成另一个特定轴(定义为Y轴)方向的偏转,也可同时实现绕沿互相垂直的X、Y轴两个方向上一定角度的偏转运动。
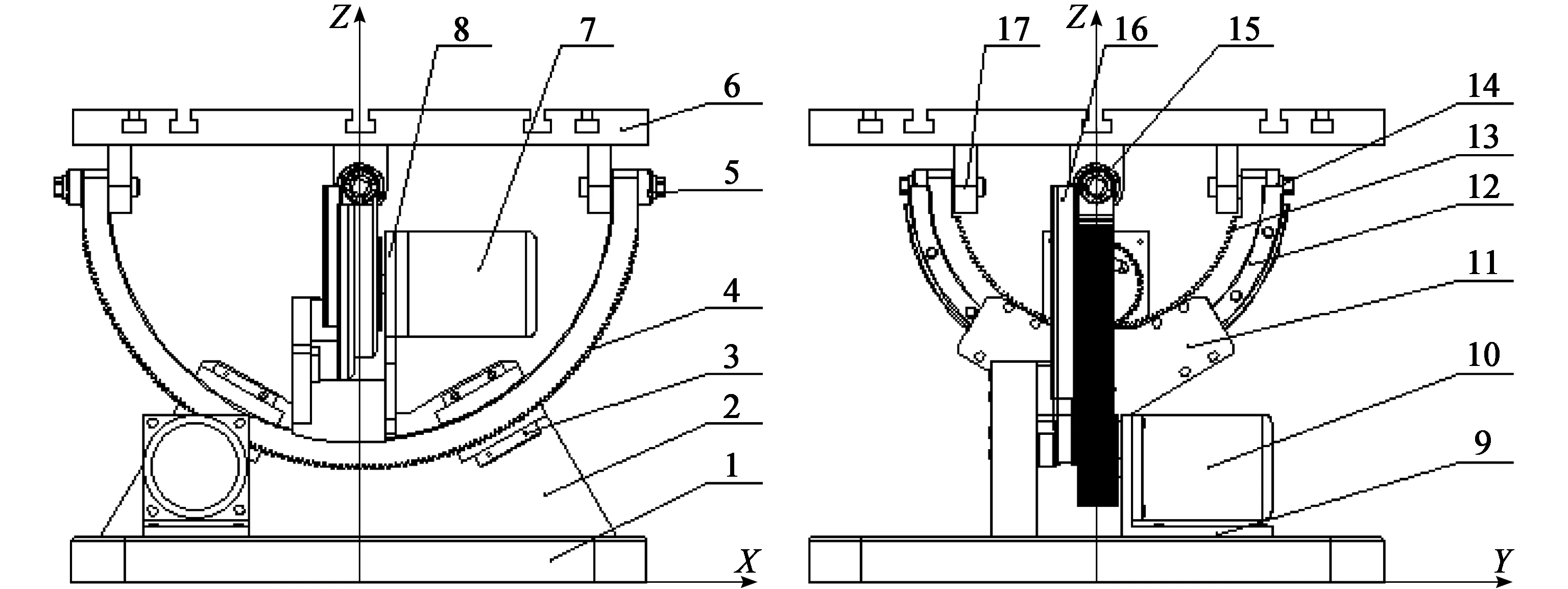
1.底座;2.外圆弧导轨支座;3.外圆弧导轨滑座;4.外齿轮拱;5.外销轴;6.台面;7.内电机;8.内电机支座;9.外电机支座;10.外电机;11.内轨连接件;12.内圆弧导轨;13.内齿轮拱;14.内销轴;15.外轴承座;16.外圆弧导轨;17.内轴承座图1 双向偏转平台二维结构图
此双向偏转平台中所用的驱动电机上安装有传递动力的齿轮,为了使该齿轮达到更高的传递精度,反向时不会产生空程误差,所以选择用消隙齿轮来解决相关问题。消隙齿轮的设计重点是齿轮中消隙拉簧的设计,现根据该双向偏转平台相关结构及参数要求对此消隙齿轮中的拉簧工作参数进行设计。
2 消隙齿轮的结构参数及消隙拉簧张紧力的计算
2.1 消隙齿轮的结构参数
以外齿轮拱啮合的消隙齿轮中的拉簧设计为例。所用驱动电机为交流永磁同步伺服电机,额定功率W=200 W、额定转矩T1=0.6 N·m,电机轴上安装有消隙齿轮。齿轮副参数见表1,消隙齿轮结构参数见图2。
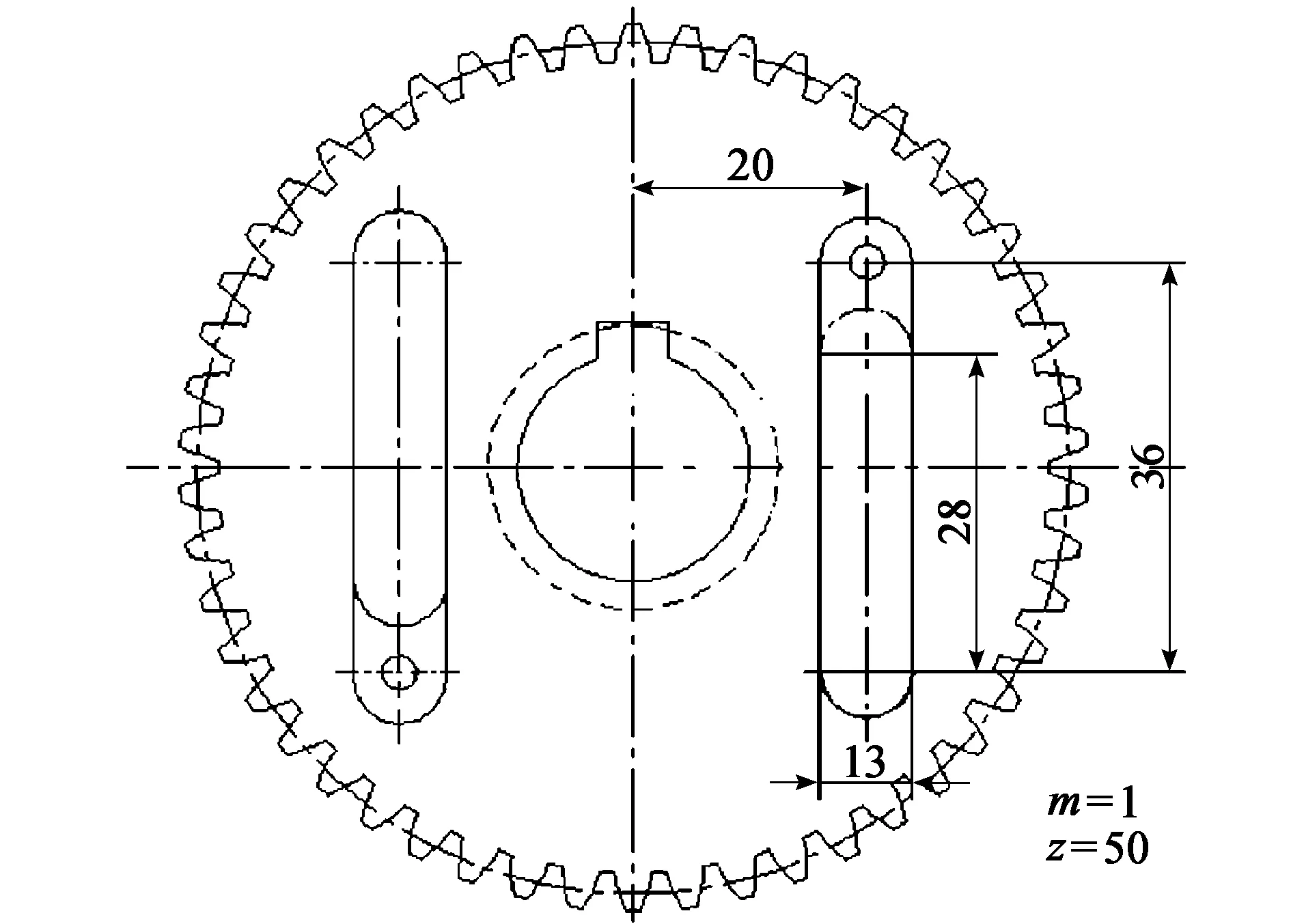
图2 消隙齿轮相关尺图
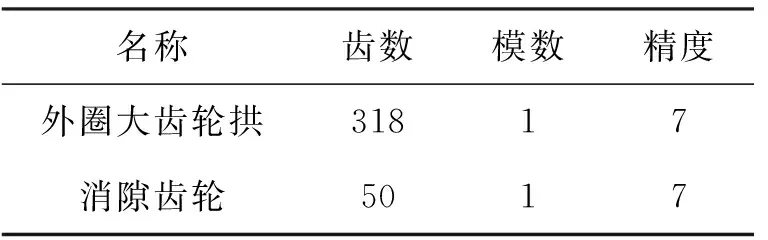
名称齿数模数精度外圈大齿轮拱31817消隙齿轮5017
2.2 消隙拉簧张紧力的计算
拉簧张紧力是拉簧设计的关键问题。拉紧力小了,拉簧不起作用;拉紧力太大可能使齿轮齿面磨损加剧,增加传动损耗,甚至齿轮卡死。消隙齿轮所传递的扭矩需要由消隙拉簧来承担,拉簧张紧力的设计原则是
T簧>T工,
(1)
式中,T簧为拉簧拉紧力所承受的扭矩,T工为消隙齿轮传递的工作扭矩。
拉簧扭矩计算公式[8]为
T簧=NFH,
(2)
式中,N为拉簧的根数,F为单根拉簧的张紧力,H为拉簧轴线距齿轮轴线的距离。
当拉簧张紧力所承受的扭矩T簧和工作扭矩T工平衡时有
T簧=T工Z2/Z1,
(3)
式中,Z1为安装消隙拉簧的主动轮齿数,Z2为从动轮齿数。
联立式(2)和式(3)单根拉簧的设计张紧力为
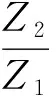
(4)
由表1和图2中显示的参数,可计算出所需拉簧的设计张紧力为
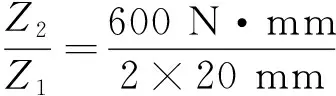
依据2.2所述拉簧设计的原则,取比计算结果稍大点的值即可,因此取F=100 N。
3 消隙拉簧的优化设计
消隙齿轮中拉簧力必须满足齿轮所传递的工作载荷的要求,拉簧外形尺寸及变形范围必须满足消隙齿轮的结构要求。基于这两方面的要求来确定该拉簧的设计参数,进而确定拉簧的具体结构。
3.1 确定设计变量
该双向偏转平台不存在高速运转的情况,在保证拉簧自身刚度、强度和几何条件达到设计要求的条件下,对拉簧进行轻量化优化,防止其自身惯性对设计结果造成非线性影响。确定拉簧钢丝直径d、拉簧中径D、工作圈数n为设计变量,即
X=(x1,x2,x3)=(d,D,n)。
(5)
3.2 确定目标函数
以拉簧质量最轻为优化目标,建立优化目标函数:
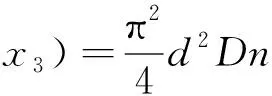
(6)
式中,d为拉簧钢丝直径,D为拉簧中径,n为拉簧工作圈数,ρ为拉簧钢丝的材料密度。舍去不影响优化结果的常数项,式(5)可变形为
(7)
3.3 建立约束条件
3.3.1 拉簧刚度的约束

图3 消隙齿轮中拉簧错齿简图
如图3所示,消隙齿轮由两个薄片齿轮组合而成,拉簧两端分别连接在不同的薄片齿轮上。拉簧须处在两薄片齿轮的拉簧槽之内,两薄片齿轮最大只能错开3个齿,才能保证拉簧与拉簧槽壁不会发生干涉。因此,根据该消隙齿轮的尺寸参数,给定两片薄齿轮间错开3个轮齿。
图3中,AB为拉簧原始状态下的长度及位置,AB1为拉簧拉伸后的长度及位置,A为拉簧在薄片齿轮之一上的钩点,B为拉簧在另一个薄片齿轮上的钩点,B1为错开3个轮齿后B的落点。AB值已知,AB1的长度可用简单几何关系求得,经计算拉簧的拉伸量为h=AB1-AB=8.2 mm。
根据2.2的分析计算,确定拉簧的最大拉力Pn=F=100 N,拉簧最小拉力P1=20 N。由文献[9]得知,拉簧刚度为
(8)
又因为
(9)
式中G为拉簧钢丝材料的剪切弹性模量(选取拉簧材料为三类碳素钢丝C级为定值79 000 MPa)。联立式(8)和式(9)得
(10)
(11)
3.3.2 拉簧的旋绕比约束
由文献[9]可知,弹簧旋绕比C=D/d取值范围介于4~16之间,其值太大会导致拉簧本身过软,此值过小卷绕时拉簧丝会受到强烈弯曲。受消隙齿轮结构限制,拉簧旋绕比取4~12,即4≤C=D/d≤12,得约束条件
g2(x)=-12x1+x2≤0,
(12)
g3(x)=4x1-x2≤0。
(13)
3.3.3 拉簧的强度约束
由文献[9]得拉簧应满足其强度要求,取最大拉力F=Pn=100 N,得约束条件:
≤[τ],
式中[τ]为拉簧材料的许用剪切应力,代入相关数值可得约束条件:
≤0。
(14)
3.3.4 拉簧安装尺寸约束
如图2,拉簧槽宽13 mm,为了不使错3个齿后拉簧与拉簧槽壁接触产生摩擦力,取D+d≤10 mm,得约束条件
g5(x)=x1+x2≤10。
(15)
3.4 求 解
利用MATLAB软件采用极大极小值法优化求解,优化过程及结果如下:
(1)所求目标函数
function f=myfun(x)
f=x(1)^2*x(2)*x(3);
(2)约束函数
function [c,ceq]=nonlcon(x) %非线性约束条件函数
c=423*(x(2)^0.84)/(x(1)^2.84)-905; %非线性不等式约束条件式(14)
ceq=9875*x(1)^4/(x(2)^3*x(3))-9.75; %非线性等式约束条件式(11)
(3)主函数程序
x0=[1;10;8]; %随机输入的初始值
A=[-12 1 0;4 -1 0;1 1 0]; %线性约束条件式(12)、式(13)、式(15)的系数矩阵
b=[0;0;10]; %线性约束条件式(12)、式(13)、式(15)的常数项矩阵
lb=zeros(3,1); %优化的下界
x=fmincon(@myfun,x0,A,b,[],[],lb,[],@nonlcon) %求解约束条件下目标函数最小值的调用函数
(4)优化结果
根据以上优化程序运行后解得:
x1=1.446 3,
x2=8.553 7,
x3=7.080 5。
4 消隙拉簧结构参数计算
要绘制拉簧工作图必须先得出的参数有:拉簧中径D、钢丝直径d、自由状态下的长度H0、最小载荷下的变形量F1、最大载荷下的变形量Fn、极限载荷下的变形量Fj,还有选取的拉簧弯钩类型和拉簧的螺旋角等。将这些参数一一求出后即可绘制出该拉簧的工作图,具体求解过程叙述如下:
根据上述优化结果,查文献[9]中的“圆柱螺旋压缩弹簧计算表11-2-19”,选取的拉簧材料为三类碳素钢丝C级,钢丝直径d=1.6 mm,中径D=9 mm,有效圈数为8圈。
由以上所选的材料、钢丝直径d及拉簧中径D,从文献[9]中的“圆柱螺旋压缩弹簧计算表11-2-19”查得三类碳素钢丝压缩弹簧相关参数如表2所示。

表2 钢丝直径1.6 mm、中径9 mm的三类碳素钢丝压缩弹簧相关参数表
现根据文献[9]中的表11-2-18对表2中的pj和fj进行修正:
pj=1810/1810×127.12=127.12 N,
fj=44×1810/(0.79×105)×1.432=1.444 mm。
以下计算根据“圆柱螺旋拉簧计算示例二”[9]进行计算:
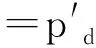
最小载荷下的变形量:F1=(P1-P0)/p′=(20-19.1)/11.1=0.01 mm;
最大载荷下的变形量:Fn=(Pn-P0)/p′=(100-19.1)/11.1=7.28 mm;
极限载荷下的变形量:Fj=fj×n×0.8=1.444×8×0.8=9.24 mm;
选圆钩型拉簧,则自由长度:H0=(n+1)d+2D=9×1.6+2×9=32.4 mm;
最小工作荷载下的长度:H1=H0+F1=32.4+0.01=32.41 mm;
最大工作荷载下的长度:Hn=H0+Fn=32.4+7.28=39.68 mm;
工作极限荷载下的长度:Hj=H0+Fj=32.4+9.24=41.64 mm;

图4 拉簧工作图
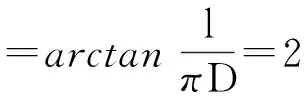
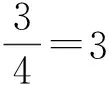
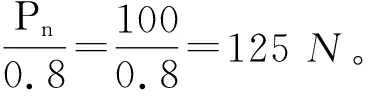
根据以上计算所得的拉簧参数,绘制图4所示的拉簧工作图。
采用文献[9]中一般方法计算出的拉簧各参数为d=1.8 mm,D=10 mm,有效圈数为11圈,拉簧质量为m=6.71 g,优化后所得的拉簧质量为m=3.47 g,优化后达到了轻量化的优化目的,优化方法可行。
5 结 论
本文以拉簧质量最轻为优化目标,以消隙齿轮传递的扭矩、消隙齿轮副的设计参数等为约束条件,对消隙齿轮中的拉簧进行了优化设计。先优化拉簧结构参数,再根据优化结果计算拉簧各工作参数,得到的结果在既保证拉簧强度和刚度等情况下,还减轻了拉簧质量,降低了消隙齿轮在转动过程中因拉簧自重的惯性对传递结果造成非线性的影响。
