1.6 m双质体卧式振动离心机有限元分析

冯朱涛

(1.中煤科工集团唐山研究院有限公司，河北 唐山 063000；2.河北省煤炭洗选工程技术研究中心，河北 唐山 063012)

1.6 m双质体卧式振动离心机有限元分析

冯朱涛1,2

(1.中煤科工集团唐山研究院有限公司，河北 唐山 063000；2.河北省煤炭洗选工程技术研究中心，河北 唐山 063012)

为确定1.6 m双质体卧式振动离心机的最佳工作点，建立该离心机的三维模型，对其进行模态分析，并研究三维模型在简谐激振力作用下的谐响应。研究表明：在四阶固有频率24 Hz时，初级振动体轴向振动位移很小，而二级振动体轴向振动位移较大，此时离心机处于理想工作状态；受迫振动时的初级振动体、二级振动体的振型和不同激振频率、不同刚度比时的振幅曲线，验证了离心机工作点选取的合理性。

卧式振动离心机；有限元分析；模态分析；谐响应分析

“十二五”以来，双质体卧式振动离心机成为我国大型选煤厂末煤脱水的主导设备。因回收率高、粉碎率低、整机易损件少、入料粒度上限高、对厂房高度要求低、维修方便、吨煤能耗低等优点，该型离心机备受选煤厂青睐。1.6 m双质体卧式振动离心机是中煤科工集团唐山研究院有限公司研发的具有独立自主知识产权的大型卧式振动离心机，也是目前国内成功运行的最大卧式振动离心机，处理量达到400 t/h。2014年1.6 m双质体卧式振动离心机在陕西燕家河煤矿选煤厂投入运行，生产实践表明：该机处理量大、运转平稳、噪声低、工艺指标优良，完全可取代进口卧式振动离心机。此外，该离心机单台价格仅为国外进口设备的1/3，配件少且寿命长，具有良好的性价比和低运行成本，推广应用前景广阔[1-3]。

为确定1.6 m双质体卧式振动离心机的最佳工作点，建立该离心机的三维模型，将其导入Algor软件进行有限元分析，并通过离心机三维模型受迫振动时的振型和振动响应曲线验证工作点选取的合理性。

1 建立模型

1.1 建模依据

1.6 m双质体卧式振动离心机主要结构参数如下：参振总质量为8.8 t，主振弹簧刚度为1.0×107N/m，支撑硬弹簧刚度为4.5×107N/m，激振频率为24 Hz。

依据1.6 m双质体卧式振动离心机的实际尺寸建立模型，在建模过程中通过施加约束来限制和定义机械系统中各零部件的连接方式和相对运动方式。将振动电机设置为轴向的简谐激振力，其余部位均设置成刚性连接；将刚度大、质量小的隔振弹簧简化成无质量的弹簧刚度，并将其内部阻尼简化成等效线性阻尼。

1.2 三维模型的建立

在三维软件中建立1.6 m双质体卧式振动离心机三维实体模型(图1)[4-5]，将模型合理简化后导入Algor有限元软件。

图1 1.6 m双质体卧式振动离心机三维实体模型Fig.1 3D model 1.6 m double mass horizontal vibrating centrifuge

将弹簧外板、外方体(加载振动电机重量)、机壳、盖门定义为初级振动体，定义支撑弹簧刚度，并使其下表面固定；将内方体、轴承、主轴、筛篮等定义为二级振动体，定义主振弹簧刚度；定义单元类型和材料属性，对三维模型进行网格划分(图2)。

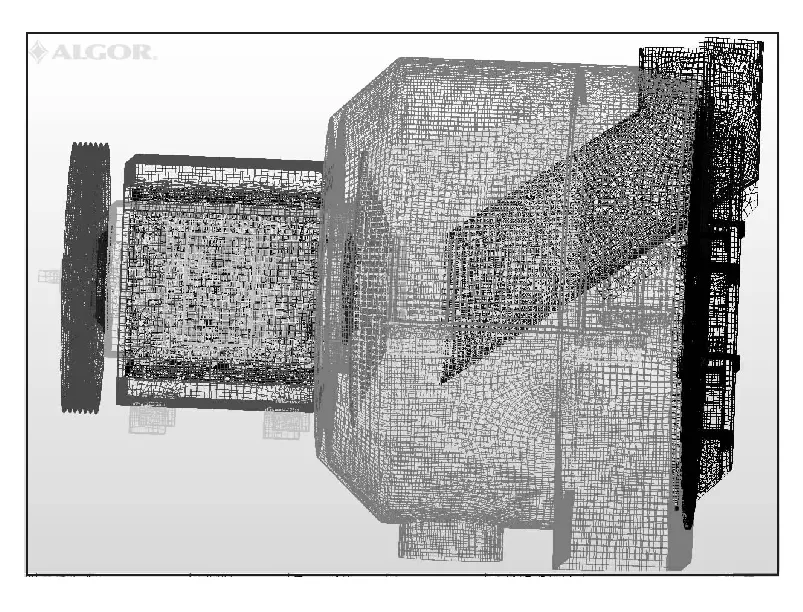
图2 单元网格划分Fig.2 Unit mesh partitioning

软件系统会自动计算出网格模型，为使单元划分更合理，谐响应分析更准确，可根据需要对模型局部进行手动细化或删除。

2 模态分析[6-8]

将图2黄色支撑弹簧底面固定，对其三维模型进行模态分析。提取前十阶固有频率中具有代表意义的五阶固有频率，各阶次与对应固有频率如表1所示。

表1 各阶次与对应固有频率Table 1 Various order and corresponding natural frequency

初级振动体、二级振动体的一阶至五阶固有频率对应的振型如图3至图7所示。

图3 各振动体的一阶振型Fig.3 First order vibration mode of different vibrating body

图4 各振动体的二阶振型Fig.4 Second order vibration mode of different vibrating body

图5 各振动体的三阶振型Fig.5 Third order vibration mode of different vibrating body

图6 各振动体的四阶振型Fig.6 Fourth order vibration mode of different vibrating body

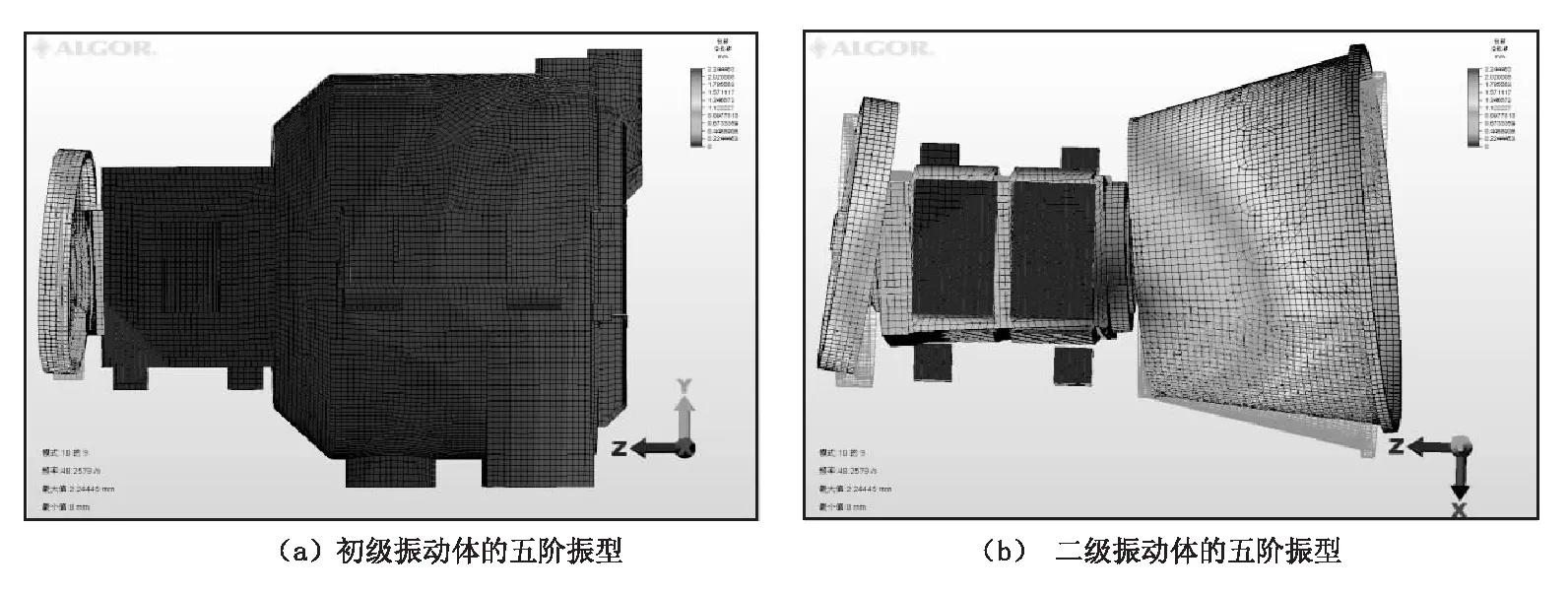
图7 各振动体的五阶振型Fig.7 Fifth order vibration mode of different vibrating body

由图3可知：在一阶固有频率下，依靠八个减振弹簧的支撑，初级振动体和二级振动体作为一个整体，在沿Y轴转动的同时沿X轴平动，且整体位移较小。

由图4可知：在二阶固有频率下，依靠八个减振弹簧的支撑，初级振动体和二级振动体作为一个整体，沿Y轴转动，且整体位移较大。

由图5可知：在三阶固有频率下，依靠八个减振弹簧的支撑，初级振动体和二级振动体作为一个整体，沿Z轴转动，且整体位移较小。

由图6可知：在四阶固有频率下，初级振动体在八个减振弹簧的支撑下无明显振动响应；主振弹簧作用于二级振动体，使其沿X轴转动，且位移较大，但整体位移很小。

由图7可知：在五阶固有频率下，初级振动体在八个减振弹簧的支撑下基本无振动响应；主振弹簧作用于二级振动体，使其沿Y轴转动，位移很大，且整体位移较大。

综上分析可知：在四阶固有频率24 Hz下，二级振动体的轴向振动位移较大，而初级振动体的轴向振动位移很小，这正是离心机工作时所需要的理想状态，说明该离心机工作时的激振频率取四阶左右固有频率最合理。

3 谐响应分析[9-10]

在实际应用中，两台相同的振动电机安装在初级振动体外方体(六面体)上，左右对称而旋转方向相反，形成一个轴向的水平惯性简谐激振力，并施加在初级振动体上。由于支撑弹簧刚度较大，初级振动体的简谐力被主振弹簧(内外方体之间的八块橡胶板)吸收，使二级振动体作轴向水平往复运动，从而实现卧式振动离心机的振动卸料。

在完成模态分析后，对该离心机三维模型进行谐响应分析。模拟离心机的两个振动电机，同时在该位置施加一个主轴方向的简谐力F，

F=F0cos2πft，

式中：F为简谐力,N；F0为振动电机激振力,取F0=80 000N；f为振动电机激振频率，依据1.6 m双质体卧式振动离心机结构特点和模态分析结果，取f=24 Hz；ζ为系统阻尼，取ζ=0.15。

在激振频率f=24 Hz时，初级振动体、二级振动体的谐响应振型图如图8所示，不同激振频率时初级振动体、二级振动体的幅值曲线如图9所示，不同刚度比η(支撑弹簧刚度与主振弹簧刚度的比值)时初级振动体、二级振动体的幅值曲线如图10所示。

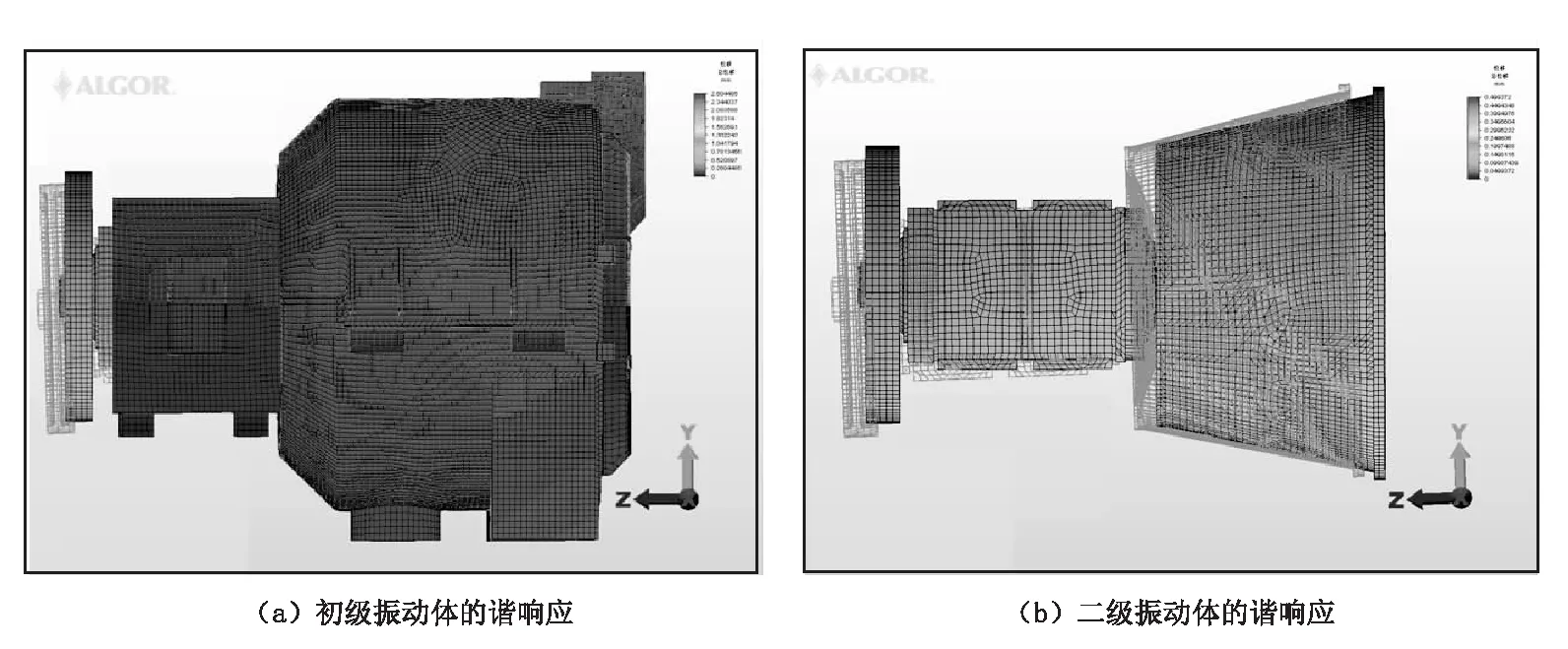
图8 各振动体的谐响应Fig.8 Harmonic response of different vibrating body

由图8可知：在激振频率为24 Hz的简谐力作用下，由壳体、盖门、外方体等组成的初级振动体呈深蓝色，说明其振幅值很小；由大带轮、主轴、内方体、筛蓝等组成的二级振动体呈浅红色，说明其振幅值较大。初级振动体振幅小，既可保证整机的稳定性又能减少能耗，而筛蓝振幅大有利于提高设备的处理能力和工作效率。

由图9可知：当激振力为80 000 N、激振频率为23～27 Hz时，可以保证二级振动体的振幅值在5 mm左右，初级振动体的振幅值远小于1 mm，这是双质体卧式振动离心机最理想的工作状态。

由图10可知：随着刚度比的不断增大，两条幅值曲线均呈下降趋势且趋于平缓，表明两个振动体的振幅在不断减小，且振幅变化幅度变小。由此来看，设计弹簧刚度时，支撑弹簧和主振弹簧的刚度比η不应小于5。

图9 各振动体不同激振频率时的幅值曲线Fig.9 Amplitude value curve of every vibrating body in different exciting frequency

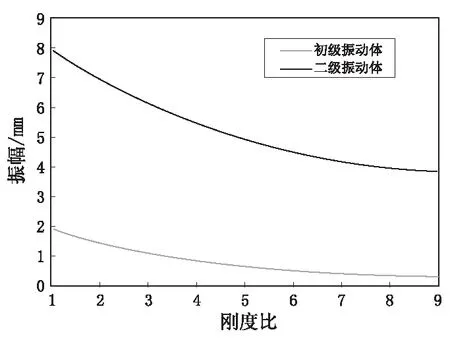
图10 各振动体不同刚度比时的幅值曲线Fig.10 Amplitude value curve of every vibrating body in different ratios of stiffness

4 结论

(1)对于1.6 m双质体卧式振动离心机来说，在四阶固有频率24 Hz下，二级振动体的轴向振动位移较大，而初级振动体的轴向振动位移很小，离心机工作状态很理想，说明该离心机工作时的激振频率取四阶左右固有频率最合理。

(2)谐响应分析表明，在激振频率为24 Hz的简谐力作用下，初级振动体振幅值很小，而二级振动体振幅值较大。初级振动体振幅小有利于保证整机的稳定性，且能减少能耗，筛蓝振幅大有利于提高设备的处理能力和工作效率，进一步验证了该离心机工作点选取的合理性

(3)设计1.6 m双质体卧式振动离心机的弹簧刚度时，支撑弹簧和主振弹簧的刚度比η不应小于5。

[1] 冯朱涛，阚晓平，赵艳平，等.1.6 m双质体卧式振动离心机参数的选取及计算[J].选煤技术，2013(2)：12-15.

[2] 陈海员，赵 立，温艳辉，等.二次激振的卧式振动离心机振动机理的研究[J].选煤技术，2008(6)：4-7.

[3] 冯朱涛，阚晓平，陈海员，等.双质体卧式振动离心机振动特性分析[J].选煤技术，2009(5)：9-12.

[4] 寇晓东,唐 可，田彩军.Algor结构分析高级教程[M].北京：清华大学出版社,2008.

[5] 叶先磊，史亚杰.ANSYS工程分析软件应用实例[M].北京：清华大学出版社,2003.

[6] 林清安.Pro/ENGINEER Wildfire2.0零件设计基础篇[M].北京：清华大学出版社,2005.

[7] 龙 飞.中文版Pro/ENGINEER产品设计完全教程[M].上海：上海科学普及出版社,2008.

[8] 刘尔烈.有限单元法及程序设计(第2版)[M].天津：天津大学出版社,1999.

[9] 赵伟封.工程结构数值分析及Algor实现[M].北京：中国电力出版社,2003.

[10] 刘长利.Algor有限元分析软件实例教程[M].北京：人民交通出版社,2005.

Finite element analysis of 1.6 m double mass horizontal vibrating centrifuge

FENG Zhu-tao1,2

(1.China Coal Technology & Engineering Group Tangshan Research Co., Ltd., Tangshan, Hebei 063000,China; 2.Coal Preparation Engineering & Technology Research Center in Hebei Province , Tangshan, Hebei 063012,China)

In order to find best operating point of 1.6 m double mass horizontal vibrating centrifuge, established three-dimensional model, modal analysis of this model is carried out as well as response is studied in condition of simple harmonic exciting force.The result shows: ideally, very small axial vibration displacement of primary vibrating body is obtained at 24 Hz four-order natural frequency, while getting bigger displacement of secondary vibrating body; in forced vibration, it is proved to reasonably determine operating point of this centrifuge by vibration mode of primary and secondary vibrating body or amplitude curves in different exciting frequency and different ratios of stiffness.

horizontal vibrating centrifuge; finite element analysis; modal analysis; harmonic response analysis

1001-3571(2015)03-0012-05

TD946.2

A

2015-05-12

10.16447/j.cnki.cpt.2015.03.004

冯朱涛(1983—)，男，安徽省颍上县人，助理研究员，从事离心脱水设备的研发与推广工作。

E-mail:47309433@qq.com Tel: 0315-7759302