一个类Lorenz系统的Hopf分岔分析及分岔控制

张中华，付景超，邓冠男

（东北电力大学理学院，吉林 吉林132012）

0 引言

1963年，美国著名气象学家E.N.Lorenz在刻画热对流不稳定性时发现了第一个混沌系统，即Lorenz系统［1］，其动力学方程表示为

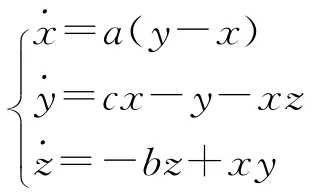
其中，x为对流强度，y为上升流和下降流的温差，z为铅直方向温度分布的非线性强度。c为Rayleigh数，为系统的主要控制参数，a是Prandt数，b是外形比。当参数时，上述系统有混沌吸引子［2－3］。

自Lorenz发现第一个混沌系统之后，人们开始不断寻找新的混沌系统，并发现了许多新的混沌系统，如Chua系统、Chen系统、Qi系统等，对这方面的研究也很多［4－7］。1994年，Sprott利用计算搜索的方法提出了19种简单形式的三阶二次混沌系统［8］，但对其中的系统进行分析的文献不多。文献［9］介绍了三维二次多项式自治混沌系统中不满足Shil′nikov定理条件的一种特殊系统，即著名的Sprott C系统：并在此基础上提出了一个新的混沌系统（称广义Sprott系统）：进一步研究了该系统的Hopf分岔及周期解稳定性。2008年，杨启贵和陈关荣提出了一个新的三维混沌系统［10］文献［11］在此基础上构造了一个新的四维自治超混沌系统，研究了系统的基本动力学行为，并设计自适应追踪控制器，实现对各种不同参考信号的单变量追踪控制。文献［12］研究了新的三维自治连续时间类Lorenz系统平衡点的存在性与稳定性，并给出了系统发生Hopf分岔和余维二退化Hopf分岔的参数条件。但上述研究主要集中在混沌的同步和控制方面，对分岔控制的研究相对较少。

本文针对文献［12］中的模型，主要研究该模型的Hopf分岔行为及分岔控制问题。

1 新的类Lorenz系统模型

考虑模型：

其中，x，y，z为状态变量，a，b，c为系统参数。

1.1 平衡点稳定性分析

引理 由文献［12］中的结论知，当a≠0，b≠0时，若bc＜0，系统（1）只有一个平衡点O（0，0，0）；当bc≥0，系统（1）有3个平衡点且当a＞0，c＜0时，平衡点O渐近稳定；b≠0，ac＞0时，平衡点O不稳定；当bc＞0，a＞0，a＋b＞0，ab（a＋b－2c）＞0时，平衡点E1，E2渐近稳定；当bc＞0，ab时，系统在平衡点E1发生Hopf分岔，且

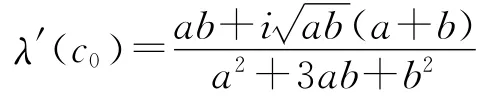
取c为分岔参数，由上面的结论知，当a＝7，b＝2，c＝c0＝4.5时，系统（1）在平衡点E1（3，3，4.5）和E2（－3，－3，4.5）处发生Hopf分岔，分岔位置如图1所示，分岔图如图2～图3所示。另外，从图2和图3可看出，系统（1）在E1和E2处的Hopf分岔方向均发生在临界点右侧。

1.2 Hopf分岔类型及周期解

首先，讨论系统在平衡点E1处的分岔类型。经计算得α′（0）＝Re｛λ′（c0）｝＝0.147 4＞0，ω′（0）＝lm｛λ′（c0）｝＝0.354 5。做变换

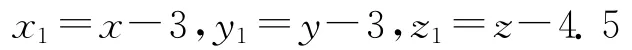
将平衡点E1移到原点。整理得

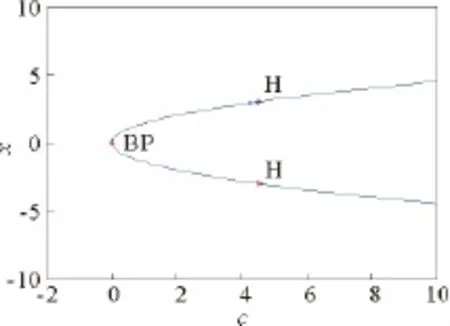
图1 平衡点分岔位置图Fig.1 Bifurcation position diagram near equilibrium

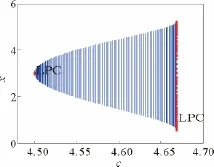
图2 系统（1）在E1处的分岔图Fig.2 Bifurcation diagram of system （1）for E1

图3 系统（1）在E2处的分岔图Fig.3 Bifurcation diagram of system （1）for E2

则系统（2）的线性化矩阵为

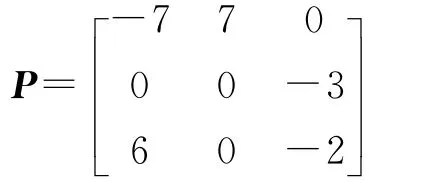
矩阵P有一对纯虚特征根λ1，2＝±3.741 7i和一个负实根λ3＝－9，设α1，α3分别为特征值λ1＝＋3.741 7i和λ3＝－9对应的特征向量。通过计算得

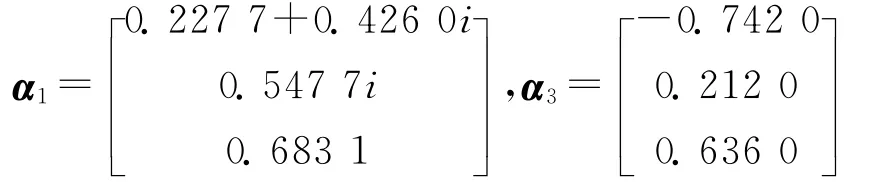
定义矩阵

作变换

系统（2）变为

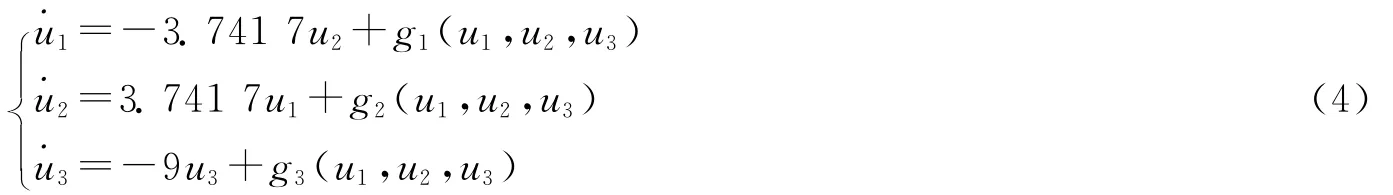
其中

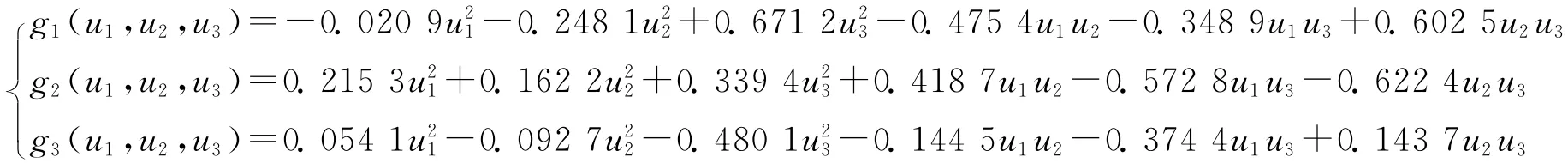
由文献［13］及上式计算得

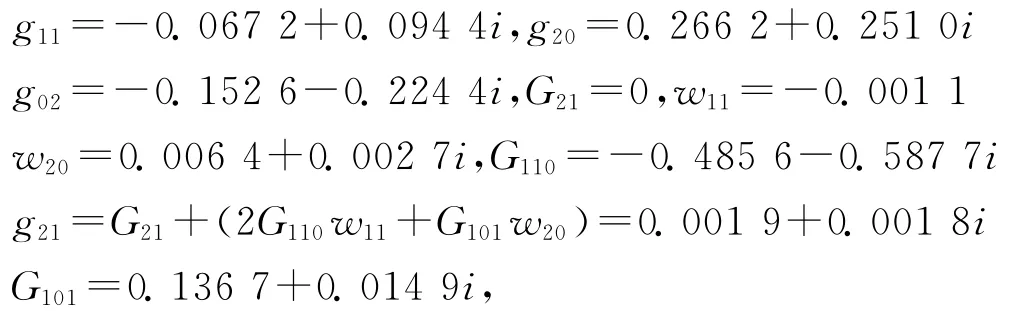
将上述结果代入式（5）

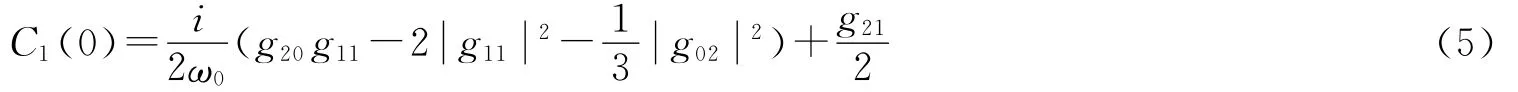
得到

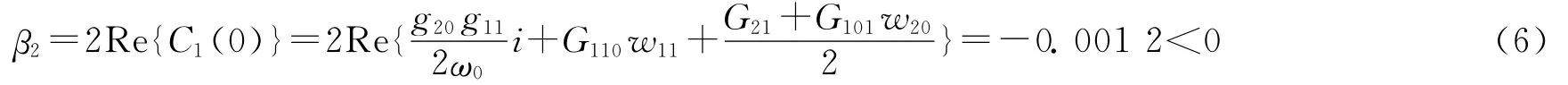
又因为α′（0）＝0.147 4＞0，由Hopf分岔理论知，系统（1）在分岔点E1处的分岔周期解是轨道渐近稳定的，产生与初始条件无关的稳定极限环，发生的Hopf分岔为超临界分岔，分岔方向为c＞c0＝4.5，这点从图2也可以看出。当c＜c0＝4.5且时，平衡点渐近稳定，如图4所示；当c＞c0＝4.5且时，平衡点不稳定并在其附近产生稳定的极限环，如图5所示。其中，仿真初值为（x0，y0，z0）＝（4.5，4.5，4.5）。

根据上面的计算结果，可以计算出重要特征向量

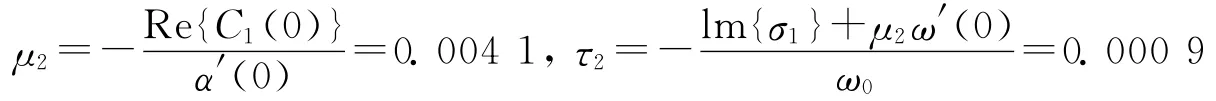
进一步得到系统的分岔周期解为

其中

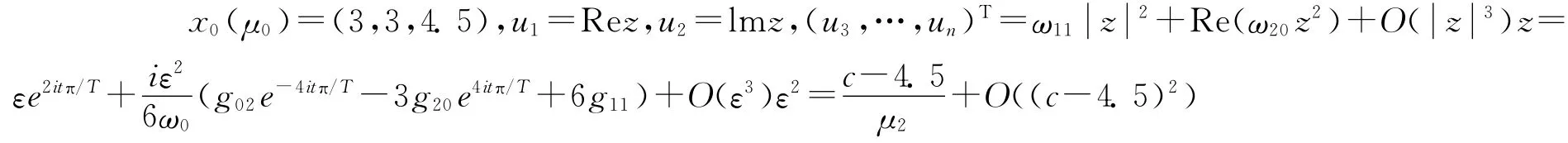
周期和特征性指数分别为

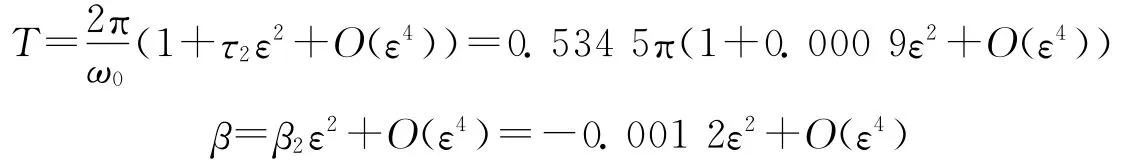
用同样的方法可判断系统（1）在平衡点E2处的分岔类型为超临界Hopf分岔，系统受扰离开平衡点将产生等幅振荡，在平衡点E2附近产生一个稳定的极限环，如图6所示。

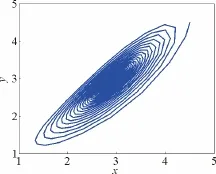
图4 c＝4.2时，系统（1）在E1处的相图Fig.4 Phase chart of system（1）at E1for c＝4.2

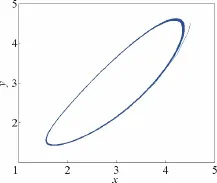
图5 c＝4.6时，系统（1）的相图Fig.5 Phase chart of system（1）at E1for c＝4.6

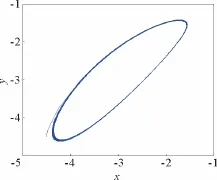
图6 c＝4.6时，系统（1）在E2处的相图Fig.6 Phase chart of system （1）at E2for c＝4.6

2 系统Hopf分岔控制

2.1 线性控制

不改变原系统的Hopf分岔点，采用线性控制器，对系统（1）作如式（8）的控制：

其中，k1，k2，k3为待定控制参数。当a＝7，b＝2，c＝4.5时，（x0，y0，z0）＝＝（3，3，4.5）。此时系统（8）变为

令

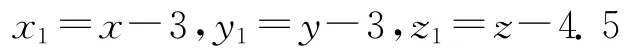
则系统（9）转化为

系统（10）在平衡点（0，0，0）的稳定性情况相当于系统（9）在平衡点（3，3，4.5）的稳定性情况。系统（10）在平衡点（0，0，0）的线性化矩阵为

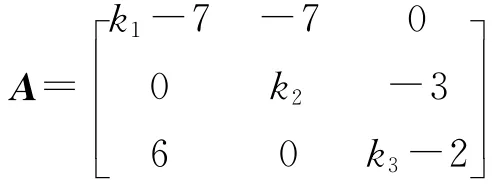
下面分3种情况讨论线性控制对Hopf分岔位置的影响。为对结果进行比较，以下的仿真初值均选为（15，3.5，7.5）。

2.1.1 k2≠0，k1＝0，k3＝0时，受控系统 Hopf分岔分析

此时矩阵A对应特征方程为

根据Routh－Hurwitz原理，方程所有的根具有负实部的充要条件是9－k2＞0，－14k2－126＞0，（9－k2）（14－9k2）＞－14k2－126。因此，当且仅当k2＜－9（k1＝0，k3＝0）时，方程所有根的实部为负数，在这个条件下，系统（10）的平衡点（0，0，0）是渐近稳定的。如取k2＝－10，k1＝0，k3＝0时，矩阵A对应特征根为λ1＝－0.138 1，λ2，3＝－9.431 0±3.528 8i。所有特征根具有负实部，系统（10）在平衡点（0，0，0）渐近稳定，进而得到系统（9）在平衡点（3，3，4.5）渐近稳定，故系统（1）在施加线性控制器后，Hopf分岔行为得到控制（见图7）。这表明可以采用只在系统（8）的第2个方程中施加线性控制器的方法来抑制Hopf分岔的出现。但有时为了表明不同线性控制器参数对Hopf分岔位置影响的不同以及它们之间的相互影响，还可以在系统的其他方程中施加线性控制器，讨论施加单个线性控制器和施加多个线性控制器对抑制Hopf分岔发生的不同影响。

2.1.2 k2＝－10，k1＝0，k3≠0时，受控系统 Hopf分岔分析

此时矩阵A对应特征方程为

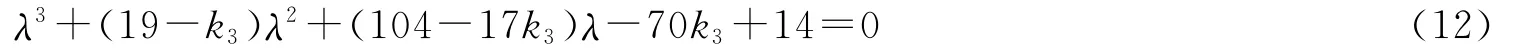
根据Routh－Hurwitz原理，当且仅当k3＜0.2（k2＝－10，k1＝0）时，方程所有根具有负实部，此时，系统（10）的平衡点（0，0，0）渐近稳定。如取k2＝－10，k1＝0，k3＝0.1，矩阵A 对应特征根为λ1＝－0.069 3，λ2，3＝－9.415 3±3.513 7i；如取k2＝－10，k1＝0，k3＝－8，矩阵A 对应特征根为λ1＝－3.762 0，λ2，3＝－11.619 0±4.192 6i。所有特征根具有负实部。所以，系统（10）在平衡点（0，0，0）渐近稳定，进一步说明原系统Hopf分岔行为得到控制（见图8～9）。

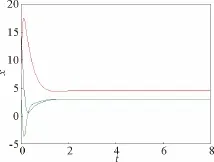
图7 k2＝－10，k1＝0，k3＝0时，系统（8）波形图Fig.7 Waveform chart of system （8）for k2＝－10，k1＝0，k3＝0

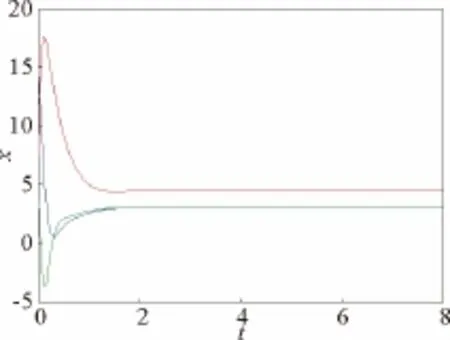
图8 k2＝－10，k1＝0，k3＝0.1时，系统（8）波形图Fig.8 Waveform chart of system （8）for k2＝－10，k1＝0，k3＝0.1

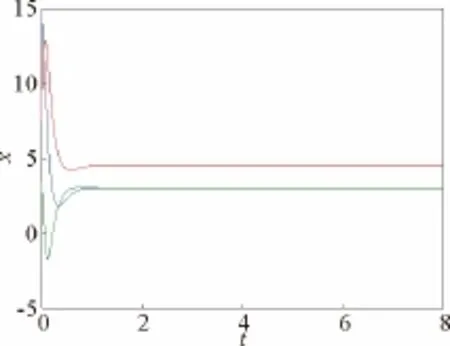
图9 k2＝－10，k1＝0，k3＝－8时，系统（8）波形图Fig.9 Waveform chart of system （8）for k2＝－10，k1＝0，k3＝－8

由图8和图9可知，当k1＝0，k2＝－10时，系统Hopf分岔点趋于稳定的速度随着k3的减小而加快。由图7和图8知，施加双线性反馈控制比单线性反馈控制的效果好，系统分岔点趋于稳定的速度更快。

2.1.3 k2＝－10，k1≠0，k3＝－8时，受控系统 Hopf分岔分析

此时矩阵A对应特征方程为

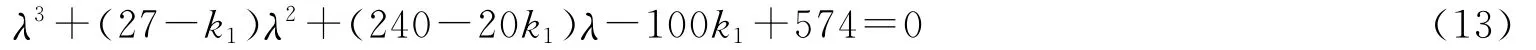
方程所有的根具有负实部的充要条件是k1＜5.74（k2＝－10，k3＝－8），在此条件下，系统（10）的平衡点（0，0，0）渐近稳定。如取k2＝－10，k1＝3，k3＝－8，矩阵A对应特征根为λ1＝－2.020 9，λ2，3＝－10.989 5±3.848 6i；如取k2＝－10，k1＝－9，k3＝－8时，矩阵A对应特征根为λ1＝－6.380 8，λ2，3＝－14.809 6±3.417 9i。所有特征根具有负实部，系统（10）在平衡点（0，0，0）渐近稳定（见图10和图11）。从图10和图11可看出，当k2，k3固定时，系统Hopf分岔点趋于稳定的速度随着k1的减小而加快。

综上可知，当线性控制参数满足一定条件时，可抑制原系统Hopf分岔的发生，进而抑制混沌的出现。

2.2 极限环幅值控制

2.2.1 基于Normal Form方法的立方非线性反馈控制

不改变原系统的Hopf分岔点，对系统（1）施加如下非线性控制器：

因为系统在平衡点的稳定性主要由系统在平衡点的线性化矩阵对应特征方程的特征根性质来判定，又因为文中讨论的平衡点是O（0，0，0），所以，影响系统在平衡点O的稳定性因素是系统的线性项部分，非线性项影响的是系统的非线性特性，比如周期解的稳定性情况及周期解幅值大小等。下面讨论非线性控制器参数对极限环幅值的影响。

令

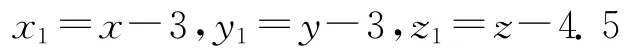
则系统（14）化为

其中，系统（15）的线性和非线性部分分别为

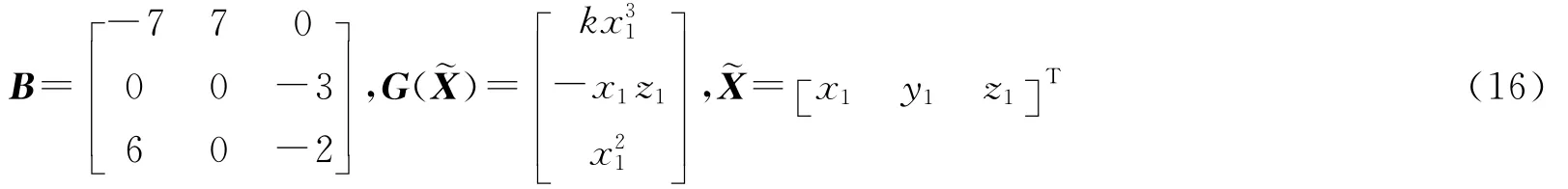
矩阵B有一对纯虚特征根λ1，2＝±3.741 7i，相应的特征向量为φ，。其中

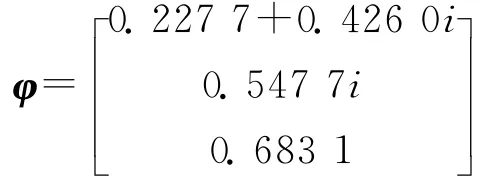
根据文献［14］中提出的计算Normal Form的直接方法，引入变换：

即可求得方程的Hopf分岔Normal Form

其中，C ＝ 〈ψ，F21〉，ψ 满足（BT－3.7417iI）ψ ＝0，〈ψ，φ〉＝1，

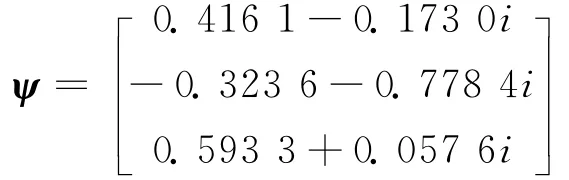
将非线性变换（17）代入非线性项中整理成关于u，u¯的多项式形式

其中，F21为u2对应的系数向量。

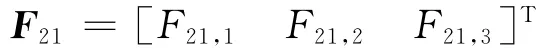
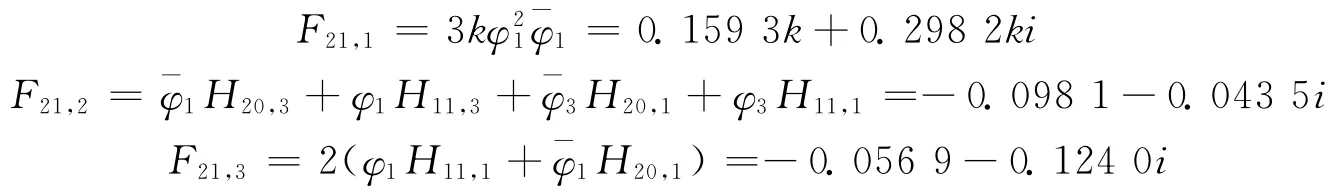
上式中，Hjk，m为向量Hjk中的第m 个元素。其中

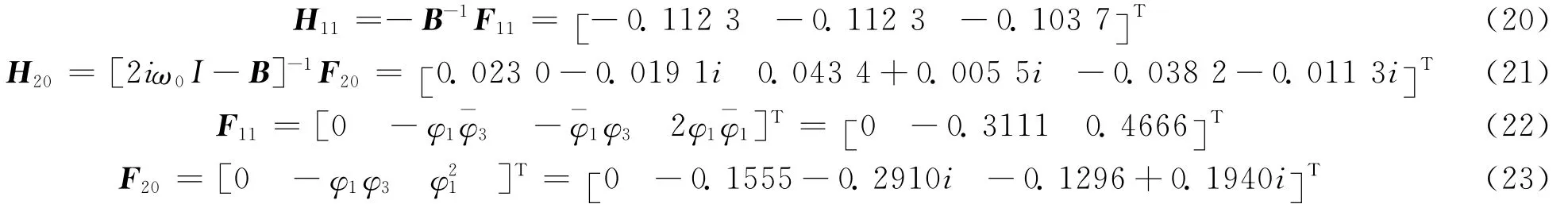
由式（20）～ （23）计算C得

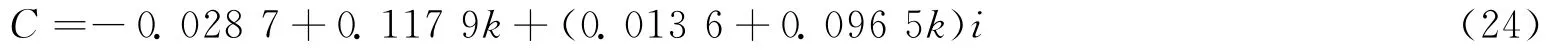
所以，式（14）的Normal Form为

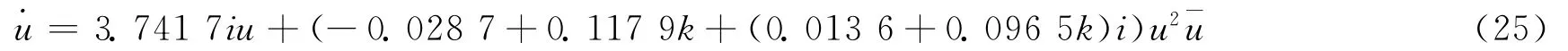
2.2.2 仿真研究

由 Hopf分岔理论知，当k＜0.243 4时，Re（C）＜0，又因为α′（0）＝0.147 4＞0，所以，系统（14）的 Hopf分岔类型为超临界分岔且Hopf分岔方向为c＞c0＝4.5，极限环稳定，极限环的幅控关系为

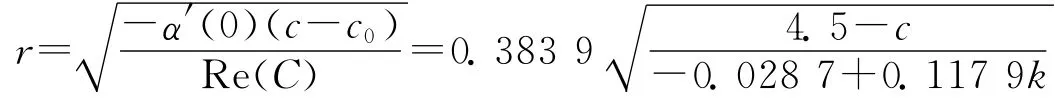
如图12所示，极限环幅值r与控制系数k是增函数关系。另外从图13和图14也可看出，振动幅值（极限环幅值）随着k的减小而减小。并且，k的范围恰好包含了k＝0的情况，与原系统的分岔类型相对应。其中，仿真初值为（x0，y0，z0）＝（4.5，4.5，4.5）。

当Re（C）＞0，即k＞0.243 4时，系统（14）的Hopf分岔类型为亚临界分岔，极限环不稳定（见图15）。

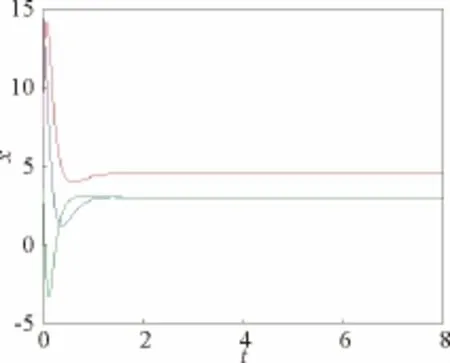
图10 k2＝－10，k1＝3，k3＝－8时，系统（8）波形图Fig.10 Waveform chart of system （8）for k2＝－10，k1＝3，k3＝－8

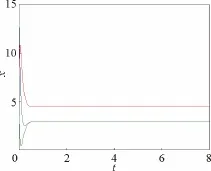
图11 k2＝－10，k1＝－9，k3＝－8时，系统（8）波形图Fig.11 Waveform chart of system （8）for k2＝－10，k1＝－9，k3＝－8

图12 受控系统（14）的限极环幅值曲线（c＝4.6）Fig.12 Gain amplitude curves for the controlled system （14）（with c＝4.6）

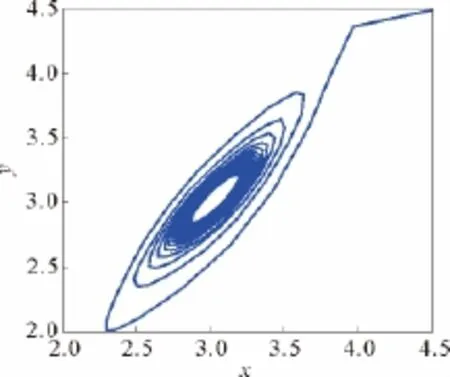
图14 c＝4.6，k＝－5时，系统（14）波形图Fig.14 Phase chart of system （14）with c＝4.6，k＝－5

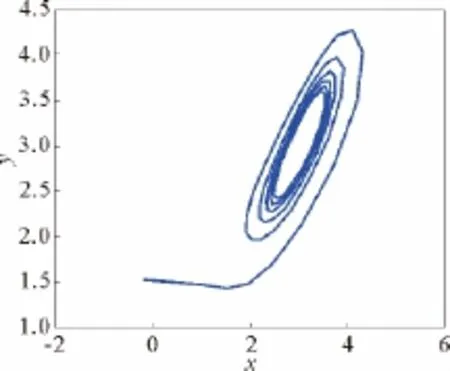
图15 c＝4.6，k＝1.2时，系统（14）相图Fig.15 Phase chart of system （14）for c＝4.6，k＝1.2

由以上分析知，当非线性控制参数满足一定条件时，可以改变原系统的分岔类型和分岔周期解振幅大小，从而实现类Lorenz系统的极限环幅值控制。

3 结论

本文主要研究了一个新的类Lorenz系统的Hopf分岔行为和分岔控制问题。首先，通过规范形方法计算出系统的稳定性指标，进而判定系统的Hopf分岔类型；然后，对系统分别施加线性和非线性控制器，并详细讨论了线性控制器和非线性控制器对Hopf分岔位置、分岔类型和分岔周期解幅值（极限环幅值）的影响，进而实现类Lorenz系统的分岔控制问题。

［1］ Lorenz E N.Deterministic non－periodic flows［J］.J Atmos Sci，1963，20：130－141.

［2］ Tucker W.The Lorenz attractor exists［J］.C R Acad Sci Pairis，1999，328：1197－1202.

［3］Stewart I.The Lorenz attractor exists［J］.Nature，2002，406：948－949.

［4］ Pang S Q，Liu Y J.A new hyperchaotic system from the Lüsystem and its control［J］.Journal of Computational and Applied Mathematics，2011，235（8）：2775－2789.

［5］ Mahmoud E E.Dynamics and synchronization of new hyperchaotic complex Lorenz system［J］.Mathematical and Computer Modelling，2012，55（7／8）：1951－1962.

［6］ Niu Y J，Wang X Y.A new hyperchaotic system and its circuit implementation［J］.Commun Nonlinear Sci Numer Simulat，2010，15（11）：3518－3524.

［7］ Mkaouar H，Boubaker O.Chaos synchronization for master slave piecewise linear systems：application to Chua′s circuit［J］.Commun Nonlinear Sci Numer Simulat，2012，17（3）：1292－1302.

［8］Sprott J C.Some simple chaotic flows［J］.Physical Review E，1994，50（2）：647－650.

［9］ 魏周超，杨启贵.基于Lorenz型系统族的三维系统的复杂动力学研究［D］.广州：华南理工大学，2011.Wei Zhouchao，Yang Qigui.Research on complicated dynamics of three－dimensional systems based on a family of Lorenz－type systems［D］.Guangzhou：South China University of Thecnology，2011.

［10］Yang Q G，Chen G R.A chaotic system with one saddle and two stable node－foci［J］.Int J Bifurc Chaos，2008，18（5）：1393－1414.

［11］李春来，禹思敏.一个新的超混沌系统及其自适应追踪控制［J］.物理学报，2012，61（4）：1－7.Li Chunlai，Yu Simin.A new hyperchaotic system and its adaptive tracking control［J］.Acta Phys Sin，2012，61（4）：1－7.

［12］李群宏，徐德贵.一个类Lorenz系统的动力学分析［J］.重庆理工大学学报，2011，25（2）：112－116.Li Qunhong，Xu Degui.Dynamics analysis of a Lorenz－like system［J］.Journal of Chongqing University of Technology，2011，25（2）：112－116.

［13］Hassard B D.Theory and Application of Hopf Bifurcation［M］.New York：Cambridge University，1981.

［14］吴志强，孙立明.基于washout滤波器的R¨ossler系统 Hopf分岔控制［J］.物理学报，2011，60（5）：1－5.Wu Zhiqiang，Sun Liming.Hopf bifurcation control of the R¨ossler system based on washout filter controller［J］.Acta Physical Sinica，2011，60（5）：1－5.