基于ADAMS的凹凸罗拉检测机构特性分析方法

贾成举

（沈阳宏大纺织机械有限责任公司，沈阳 110141）

k——弹簧刚度；

l——弹簧作用点到转动中心的距离；

m——集中点质量；

a——集中点质量到转动中心的距离；

ms——刚性杆质量。

单自由度无阻尼的质量—弹簧振动系统在外部激振力的作用下将进行强迫振动，其振动过程有如下特点［2］：① 在简谐激振力的作用下，振动系统所产生的强迫振动是简谐振动，振动频率与激振力频率相同；② 强迫振动的稳态振程和相位角仅取决于振动系统本身的物理特性和激振力的大小与频率，与初始条件无关，初始条件只影响系统的瞬态振动；③ 强迫振动的振程大小，动力放大系数β（也就是稳态振程X与静力位移X0之比）只与频率比λ（激振频率ω与固有频率ωn之比）和阻尼比ζ（粘性阻尼系数C与临界阻尼系数CC）有关。

0 引言

在并条机的自调匀整系统中，棉条由导条架经给棉罗拉进入由凹凸罗拉构成的检测机构，随着喂入棉条的线密度差异，检测机构的凹凸罗拉上下摆动，伺服电机则根据位移传感器的检测信号控制牵伸罗拉的转速以实现自调匀整。随着高速并条机的不断发展，要求凹凸罗拉检测机构应该有更高的响应特性。

笔者利用机械系统动力学自动分析仿真软件ADAMS对凹凸罗拉检测机构进行动力学分析，比较检测机构中各零件对响应特性的影响，为优化设计的方向和提高检测机构的性能提供了依据。

1 凹凸罗拉检测机构模型

凹凸罗拉检测机构工作原理如图1所示，摆臂OC绕O点旋转，由于喂入棉条线密度差异而在A点给摆臂施加一作用力，位移传感器在B点检测摆臂的位移，弹簧在摆臂末端C点对摆臂施加作用力以保持凹凸罗拉对棉条的正常压力。

由于检测机构在工作过程中摆动的幅度较小，受到的空气阻力可以忽略不计，故其属于无阻尼振动系统；根据其工作原理，属于单自由度振动系统，其系统组成主要有集中质量、刚性杆和弹簧，其振动系统如图2所示。

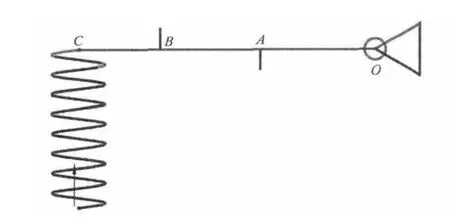
图1 凹凸罗拉检测机构工作原理

图2 凹凸罗拉检测机构振动系统

故机构的固有频率f为［1］：

式中：

k——弹簧刚度；

l——弹簧作用点到转动中心的距离；

m——集中点质量；

a——集中点质量到转动中心的距离；

ms——刚性杆质量。

单自由度无阻尼的质量—弹簧振动系统在外部激振力的作用下将进行强迫振动，其振动过程有如下特点［2］：① 在简谐激振力的作用下，振动系统所产生的强迫振动是简谐振动，振动频率与激振力频率相同；② 强迫振动的稳态振程和相位角仅取决于振动系统本身的物理特性和激振力的大小与频率，与初始条件无关，初始条件只影响系统的瞬态振动；③ 强迫振动的振程大小，动力放大系数β（也就是稳态振程X与静力位移X0之比）只与频率比λ（激振频率ω与固有频率ωn之比）和阻尼比ζ（粘性阻尼系数C与临界阻尼系数CC）有关。

2 凹凸罗拉检测机构动力学分析

在确定了检测机构的工作原理、振动类型、约束条件等后，就可以进行ADAMS的动力学分析了，在ADAMS／VIEW中建立三维实体模型［3］，也可以将已有实体模型通过IEGS标准格式文件导入到ADAMS中，添加载荷、约束、设定弹簧刚度、初拉力等已知参数［4］。

2.1 不同激励频率分析

因喂入凹凸罗拉检测机构的棉条线密度偏差是随机发生的，无规律可循，而且不同品种的棉条平均重量偏差率也有差异，因此在对比分析不同检测机构的性能时，可以取检测机构的固有频率f的一定倍数激励频率［5］，例如0.01f、0.03f、0.06f、0.1f、0.3f、0.8f作为输入条件来加以比较，图3为通过设定不同输入条件后位移传感器所处位移在振动过程中的位移变化规律。

图3 凹凸罗拉检测机构1Hz外部激励设定

2.2 弹簧刚度对振动稳态过程的影响

为了便于检查机构初始值的标定，需对所检查的弹簧施加一个预紧力，一般为在凹凸处产生60N的压紧力；而针对不同的品种，如精梳、普梳、混纺等，需选用不同刚度的弹簧，使检查机构保持良好的响应特性［6］。图4为弹簧刚度k＝28.7N／mm，在0.5 Hz外界激励作用下的弹簧振程曲线，从图4中不难看出当时间达到0.75s时，弹簧的振动已基本达到稳态振动［7］。

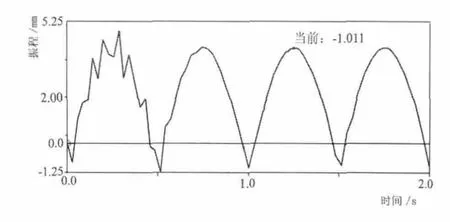
图4 凹凸罗拉检测机构在0.5Hz外部激励作用下的弹簧振程曲线

2.3 开车阶段稳态过程分析

根据单自由度无阻尼的质量—弹簧振动系统的特点，其振动频率与激振力的频率相同，但从启车到检测系统达到振动平衡即与激振力同频率振动还需要一个过程；虽然这个过程十分短暂，但是在达到振动平衡之前，其随机振动的振动状态将影响到检测精度，并随车速的不断提高而使开车初始阶段的条干CV值超标棉条的长度逐渐加大［8］。通过ADAMS的振动状态仿真，可以观察到不同系统的平衡状态过程，如图5所示，以比较优化的结构，降低启车短片段的影响。

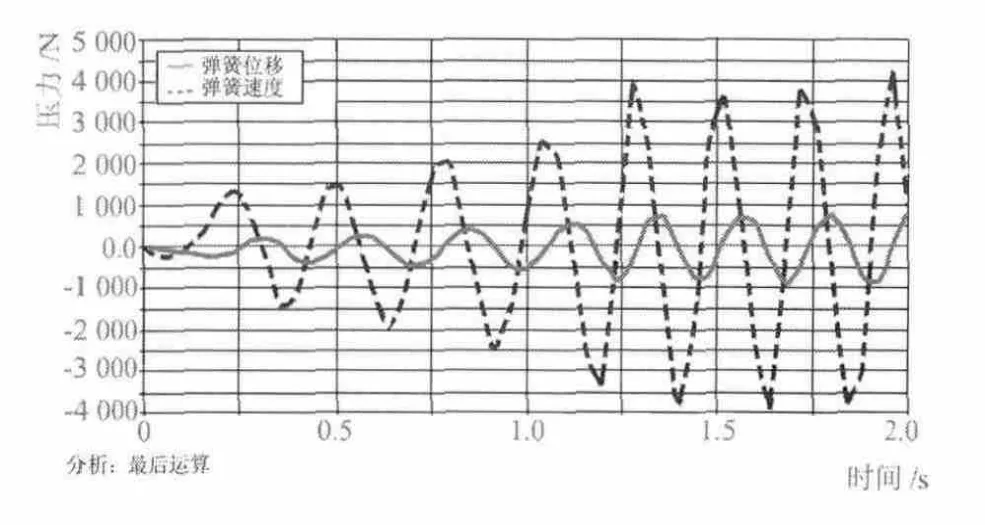
图5 凹凸罗拉检测机构弹簧位移与速度曲线

2.4 检测机构动能分析

单自由度无阻尼的质量—弹簧振动系统的振动特性是以忽略弹簧重力为前提的，因为在绝大多数情况下，弹簧重力对系统的影响很小。凹凸罗拉检测机构的力学模型可以简化为单自由度无阻尼的质量—弹簧振动系统，但又不完全等同。为了提高检测机构的响应特性，检测机构的摆臂多采用轻质材料来降低振动转动惯量，当弹簧自身的惯性力相对于摆臂较大时，相当于给系统施加了一个时刻在变的阻尼。虽然弹簧在振动过程中对凹凸罗拉的惯性力计算较为复杂，但可通过振动过程中两者的动能来进行比较，弹簧和摆臂的速度曲线如图6所示。

图6 凹凸罗拉检测机构弹簧与摆臂速度曲线

由于弹簧在振动过程仅有发生弹性变形的一部分参与运动，故按能量守恒关系［9］，弹簧的动能为：

式中：

m——弹簧质量；

v——弹簧速度；

k——弹簧刚度；

x——弹簧变形量。

从弹簧变形量曲线中可更加方便地计算出弹性势能，进而求出弹簧在运动过程中的动能。

3 结语

3.1 根据凹凸罗拉检测装置的工作原理，分析了检测装置力学模型及振动类型、固有频率的计算方法及振动过程中具有的特点。

3.2 运用ADAMS对检测机构进行动力学分析，提出确定启车过程系统响应特性、比较不同弹簧刚度对系统稳态过程的影响和计算弹簧运动惯性力的方法，确定了适合高速检测的检测机构固有频率和弹簧参数。

［1］成大先.机械设计手册：第3篇［M］.北京：化学工业出版社，2002.

［2］倪振华.振动力学［M］.西安：西安交通大学出版社，1989：120－138.

［3］王国强，张进平，马若丁.虚拟样机技术及其在ADAMS上的实践［M］.西安：西北工业大学出版社，2002.

［4］李军，邢俊文，覃文洁.ADAMS实例教程［M］.北京：北京理工大学出版社，2002.

［5］王建军，高雄兵，李其汉.单自由度参数振动系统非线性响应的若干特征［J］.应用力学学报，2003，20（2）：147－151.

［6］姜占方.单自由度非线性系统自由振动的数值解［J］.青海师范大学学报（自然科学版），2003（2）：25－28.

［7］李海姣，张维锦.振动时间对无阻尼单自由度简谐振动共振时振幅的影响［J］.工程建设与设计，2005（2）：47－50.

［8］张智慧，李秀风.基于MATLAB的单自由度系统阻尼影响分析［J］.机械制造与自动化，2012，41（4）：131－132.

［9］闻邦椿.振动机械的理论与动态设计方法［M］.北京：机械工业出版社，2001：132－133.