利用小波变换对纺织品在线监测图像的处理
2015-12-19谭燕玲周献珠
谭燕玲,周献珠,张 强
(1.新疆轻工职业技术学院,乌鲁木齐,830021;2.新疆大学 电气工程学院,乌鲁木齐,830047)
0 引言
随着新疆纺织业的迅猛发展,用户对纺织品质量要求提高,大量纺织厂广泛应用了在线监测技术,其中包括对纺织品质地、颜色、图案等的监测。然而,对监测信号深层次处理一直是制约在线监测发展的一个瓶颈[1-3]。笔者基于小波在信号处理方面的强大功能,利用小波分析对纺织品图案和染色监测图样进行单元个体编码、图样去噪、分解、增强及锐化等多方面深层次处理,为纺织品的图案和染整的控制做好前期准备。
1 利用小波对图样的构成单元进行编码
1.1 采集图样
完善的纺织品生产过程离不开可靠的在线监测系统,然而监测系统受到光线、粉尘、电磁信号干扰等各方面因素影响,导致监测图像模糊不清。这样的监测信号图像,微机无法直接进行后台分析。编写小波程序1(如图1)的监测花布图样fabric,无论是背景亮度均匀程度或图案的清晰度均不理想。
程序1:clear,close all;
ii=imread(’fabric.tif’)
imshow(ii)

图1 花布监测图样
1.2 图样背景亮度估计
从图样1可以看出检测图像亮度不均匀,中心位置背景亮度高于其他部分的亮度。利用小波程序2对花布图样fabric进行亮度估计分析,生成的背景图如图2所示,三维背景表面图见图3。
程序2:background=imopen(ii,strel(’disk’,15));
imshow(background)
figure,surf(double(background(1:8:end,1:8:end))),zlim([0 256]);
set(gca,’Ydir’,’reverse’);
图2 背景图
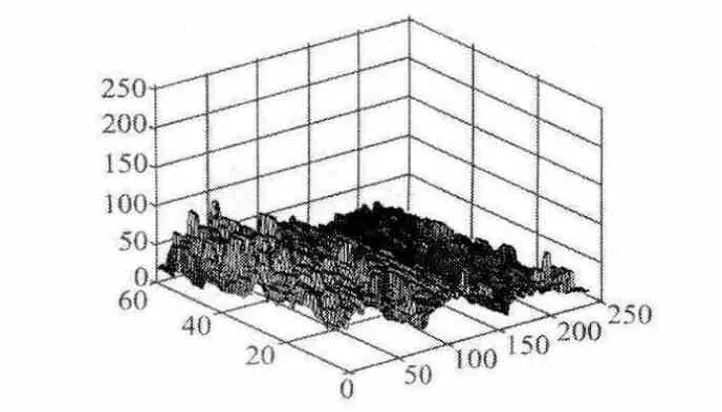
图3 三维背景表面图
1.3 原始图像减去利用小波程序提取的背景图样
编写小波程序3,现从监测图样1中减去背景图2,如图4。处理完毕后,比较图1和图4,图样背景亮度均匀度已有所改善。
程序3:i32=imsubtract(ii,background);
figure,imshow(i32)

图4 除去背景后的图样
1.4 调节图样对比度以改善图样的清晰度
从图4可以看出处理后的图样对比度并不理想。因此,编写程序4,调节图样的对比度,调节后的花布图样如图5所示,相比图4其图样的清晰度明显提高。
程序4:i33=imadjust(i2,stretchlim(i2),[0 1]);
figure,imshow(i33)

图5 调节对比度后的图样
1.5 利用阈值操作将图样转换为离散的二进制图样
要对图样进行深度处理,需要将采集的模拟信号离散化,转化为二进制数据。因此,利用程序5将图样5转化为离散的二进制图样,以便微机对花布图样fabric图案进行分析、处理、定位和诊断。
程序5:level1=graythresh(i33);
bww=im2bw(i33,level1);
figure,imshow(bww)
1.6 确定并统计图样单元的数目
编写程序6,用来分析二进制图样中所有单元,并返回相应单元数目,运行后可以统计出fabric共有2 313个单元。
程序 6:[labeled,numobjects1]=bwlabel(bww,4)
numobjects 1=
2313
1.7 对二进制图样单元的准确定位
编写小波程序7,移动鼠标到达所需要定位的图样单元时,将显示个体在图样中的坐标位置及背景像素。运行程序,结果为单元定位,如图6所示,可以看出图像为第1 652个单元个体,背景颜色为RGB 0.714,0.714,0.714,位置为x:476,y:348。
程序7:grain1=imcrop(labeled)
1652

图6 图中单元个体的定位
通过以上步骤实现了检测图像由整体到个体,实现了图样的转换和定位,为后期图样处理提供了必备条件。
2 基于二维静态小波对监测图样进行深层次频域分解
对纺织品监测图样本质的研究是获得图样深层次信号细节的唯一途径。采集图样信号往往包含各种高低频信息,利用对信号频域的分解可客观地获得图样的各种细节信息,分解的层数越多,越有利于揭示图样的细节信息。笔者采用二维静态小波的高通滤波器和低通滤波器对监测图样进行频域分解,利用小波的db1编写程序8对采样丝绸图样julia1从近似、水平、竖直、对焦4个角度进行频域3层处理,分解出12个图像,如图7所示。从level3中可以看出有大量的噪声信号聚集在高频信号中,影响了图像的清晰度;而对高频信号的去噪是图像清晰化的重要手段。

图7 用小波分析图样julia1
程序8:close all
clear
load julia1
[swa,swh,swv,swd]=swt2(X,3,’db1’);
whos
colormap(map)
kp=0;
for ii=1∶3
subplot(3,4,kp+1),image(wcodemat(swa(:,:,ii),192));
title([’approx,cfs,level’,num2str(ii)])
subplot(3,4,kp+2),image(wcodemat(swh(:,:,ii),192));
title([’Horiz,det.cfs,level’,num2str(ii)])
subplot(3,4,kp+3),image(wcodemat(swv(:,:,ii),192));
title([’vert,det.cfs,level’,num2str(ii)])
subplot(3,4,kp+4),image(wcodemat(swd(:,:,ii),192));
title([’diag,det.cfs,level’,num2str(ii)])
kp=kp+4;
end
3 利用小波分析对监测图样高频信号部分进行去噪处理
噪声信号的来源是随机的,过多的噪声将严重影响监测图样的质量,进而影响对图样的整个过程处理和分析。噪声信号,一方面在图像采集过程中要尽可能弱化,另一方面对采集完毕的图样也要利用软件手段进行去噪处理。去噪已成为影响图像处理效果极其重要的一部分。二维小波处理二维图像信号优势在于对图像的深层次频域分解,可根据噪声所在的频域进行滤波处理以达到去噪的目的。
其步骤为:① 小波分解,即选择分解层次N,然后从第1层到第N层的分解,并对每一层进行高频系数阈值量化处理。② 对信号的重构,即对量化后各层高频系数进行小波重构。
对图像julia编写程序9去噪,去噪过程如图8所示,可以发现去噪效果良好。
程序9:load julia1;
subplot(224);image(X);colormap(map);
title(’原始图像’);
axis square
init=2055615866;
randn(’seed’,init)
x=X+38×randn(size(X));
subplot(221);image(X);colormap(map);
title(’含噪声图像’)
axis square
[c,s]=wavedec2(x,2,’sym4’);
a1=wrcoef2(’a’,c,s,’sym4’);
subplot(222);image(a1);
title(’去噪图’)
axis square
a2=wrcoef2(’a’,c,s,’sym4’,2)
subplot(223);image(a2);
title(’完全去噪处理后的图像’)
axis square;
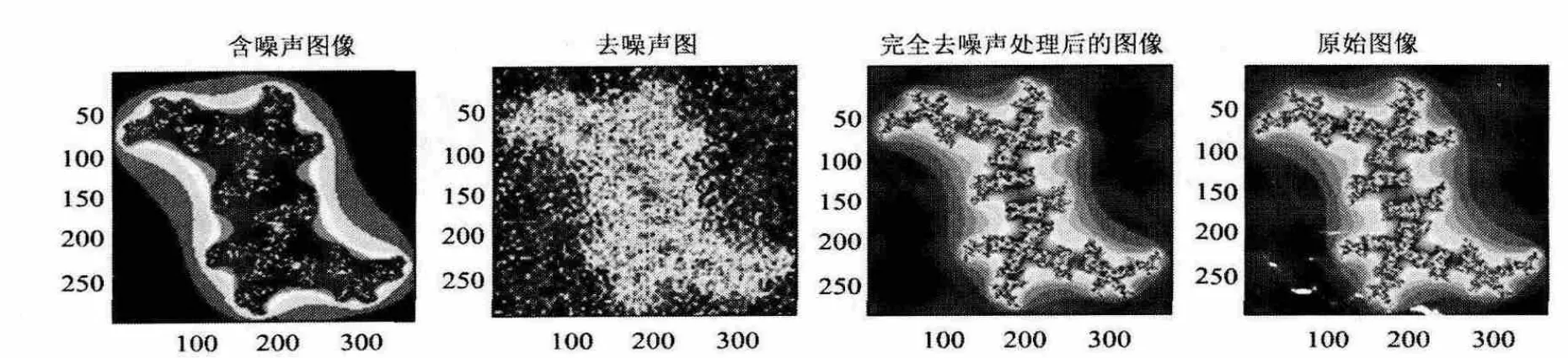
图8 图样julia1去噪处理效果对比
4 对重构信号低频部分进行小波增强处理
重构的图样视觉上比较模糊,图像质量不高,主要是图像的灰度不高,对比度不够。小波增强技术不能改变图像本身所包含的特征信息,但是可以凸显其特征。从某种意义上看,小波增强的目标就是放大图样中特征信息的对比度,增强图样的可理解性,提高视觉质量[4-5]。对于图像julia1,由于经过二维小波db1分解后,图像的轮廓主要集中在低频部分,细节部分体现在高频部分。因此对低频分解系数增强处理,可以提高图像对比度,增强图样特征量,提高图样质量。如图9所示。
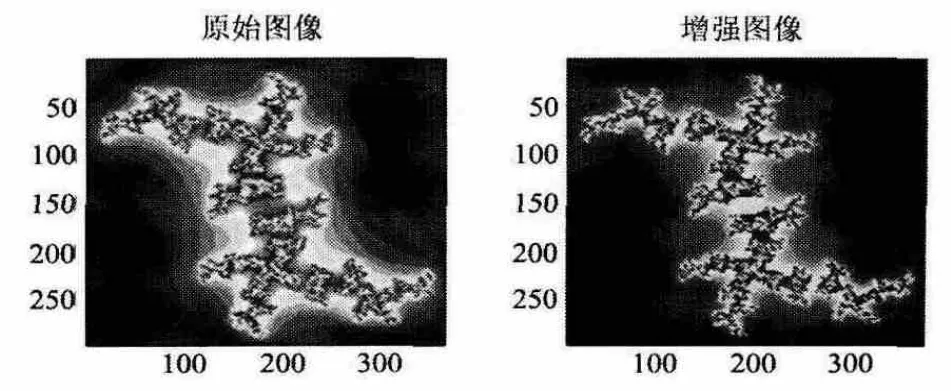
图9 利用小波增强图样julia1
5 对重构信号高频部分进行小波锐化处理
高频部分是获得细节信号的主要部分,而小波锐化就是突出高频信息,并从高频信号中分离出定位系统特征或子系统成分,以便进一步分析和处理。对图样julia1进行锐化处理,比较DCT方法和小波处理的结果。处理过程如图10所示,从结果中可以看出,DCT方法得到的是图像边缘上的低频信息,而用小波方法得到不仅是边缘低频成分的信息,还能反应低频变化的内容及高频成分。
6 利用小波对采样图样进一步多样化处理
对布匹图样flower进行各种方法处理,略去程序和处理过程,效果如图11所示。
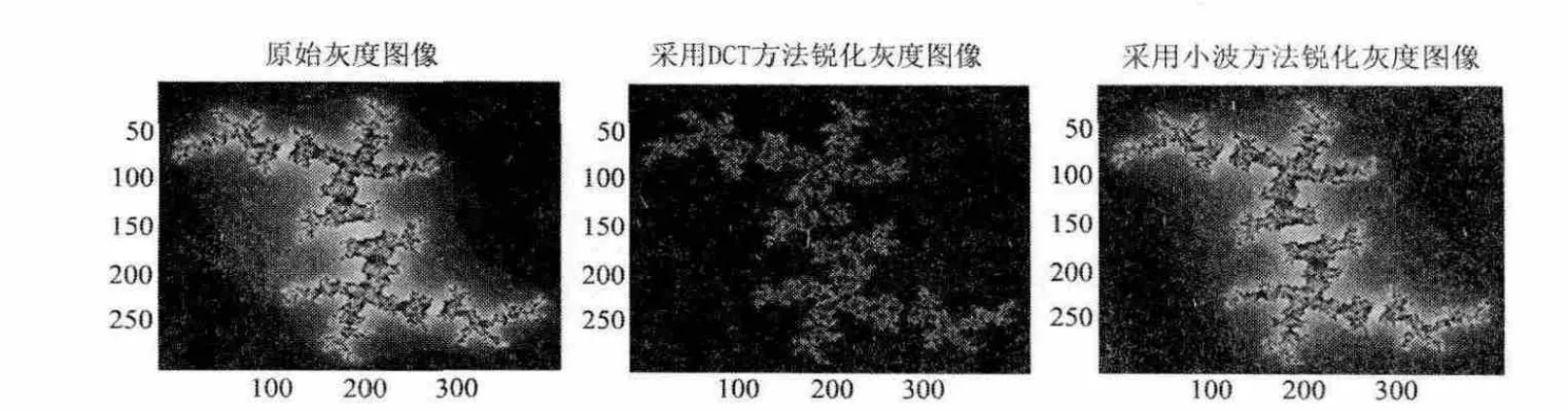
图10 DCT方法和小波锐化图样效果对比
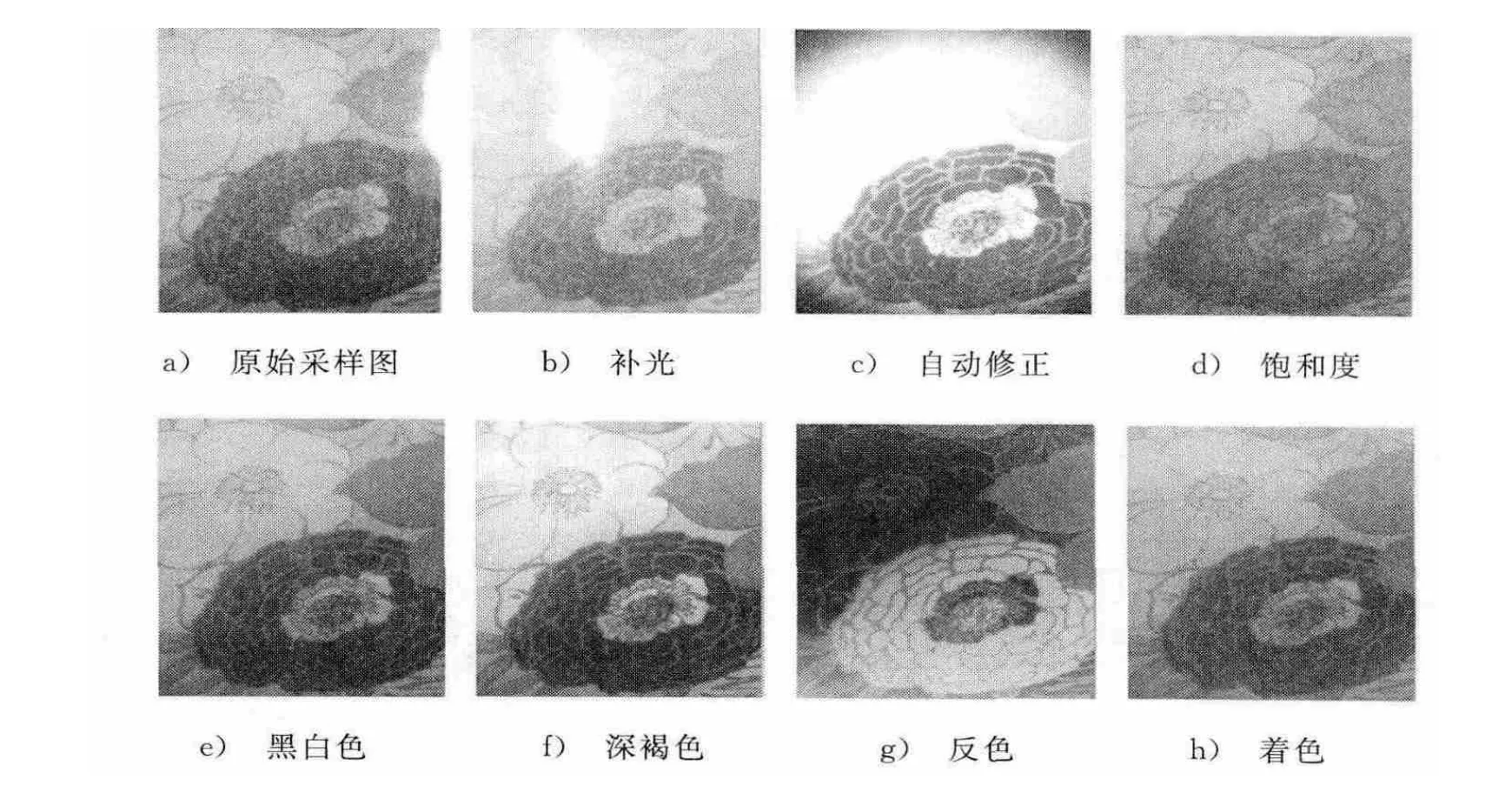
图11 对采样图样flower图形处理
7 结语
随着对纺织产品在线监测度的提高,如何处理监测图样,并对监测信号进行深层次处理成为技术瓶颈。由于监测图像受到噪声、光线强弱等因素影响,已经具备了一定的失真度,而笔者采用小波对监测的图像信息进行了多方面处理,使图样均匀度、清晰度明显提高,为后期纺织产品质量判断和染整控制提供了科学依据。
[1]董延华,王慕坤.小波变换在图像压缩中的应用研究[J].吉林师范大学学报,2005,5(2):38-43.
[2]薛文,宋国乡.提升的M通道小波变换在图像压缩中的应用[J].计算机应用,2005,25(12):31-36.
[3]于贵江,孟绍良,李继征.小波变换在图像压缩中的应用[J].大连海事大学学报,2005,31(6):9-14.
[4]张德丰.MATLAB小波分析[M].北京:机械工业出版社,2010.
[5]成礼智,王红霞.小波的理论与应用[M].北京:科学出版社,2004.
