随机车流作用下桥梁冲击系数分析
2015-12-19殷新锋
殷新锋,邓 露
(1.长沙理工大学 土木与建筑学院,湖南 长沙 410004; 2.湖南大学 土木工程学院,湖南 长沙 410082)
单一移动车辆对桥梁结构产生的振动响应问题研究已经较为成熟.以往的车-桥耦合振动的分析中,大多数学者选择单个的三维车辆模型[1-4],或者仅仅考虑一个确定的车列荷载[3-5].近年来,虽少数研究者开始将研究重点转移到随机车流作用下桥梁振动响应分析,如韩万水,Chen S.R.等,但还未形成统一结论[5-9],且针对冲击系数的研究仍然相对较少.冲击系数作为一个重要参数被广泛运用在桥梁设计中,因此,随机车流作用下桥梁的冲击系数分析显得尤为重要.
由于随机车流本身存在较大的不确定性,使得冲击系数的研究较为困难,主要表现为:首先,由于多车道、多向行驶以及各个车辆的行驶速度不同导致车辆间的相对位置不断变换,使得最大静挠度的确定十分困难;其次,随机车流中车辆数较多且类型复杂,如车辆均采用三维模型模拟,计算最大动挠度时,则计算量将较大.
本文提出了简便且实用的随机车流下桥梁结构冲击系数计算方法:首先根据响应面分析方法,拟合影响面的函数表达式,将确定最大静位移时随机车流布载位置的问题转变为求函数的最大值问题,从而获得随机车流作用下桥梁结构最大静挠度;其次在计算最大动挠度时,根据已编制的车-桥耦合振动分析程序和随机车流中各类车型的三维模型,获得各类车型单独作用下车-桥耦合接触力并等效代替各类车辆三维模型作用在桥梁结构上,这样便可将三维车辆模型作用等效转化为随机接触力作用在桥梁结构,从而获得随机车流作用下桥梁结构的动力效应,基于统计分析,求得随机车流作用下桥梁结构冲击系数.
1 随机车流模拟
1.1 公路桥梁随机车流分类
按照全国高速公路管理部门制定的收费标准,根据车辆装载货物或乘客的能力大小将所有车辆划分为12小类,具体分类见文献[7].
1.2 随机车流数据分析
公路车流拥有较强的随机性,通过对实测数据进行分析整理,下面仅给出随机车流主要参数按时间段进行分类的统计分析结果.限于文章篇幅,仅给出车型、车道及车重分析.
1.2.1 车型分析
本次调查历时24h,共采集到13 874辆的车流数据,将实测车流数据按本文的车型分类并进行分类统计,具体数据见表1.
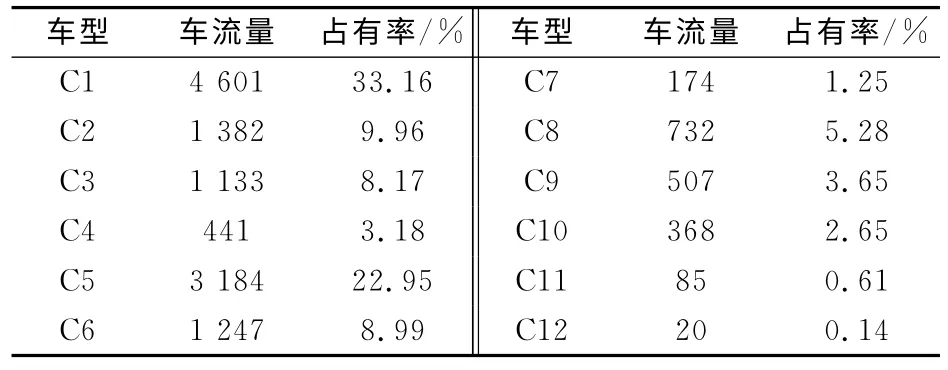
表1 车型占有率Tab.1 Occupancy of vehicles
1.2.2 车道分析
车辆作用在桥梁横向上的不同位置会得到不同的动力荷载效应,所以很有必要考虑车流在车道上的分布.根据实际测量的数据,选取某一时刻下,C1车型到C12 车型在超车道、第一行车道、第二行车道上的分布比例进行分类统计,如图1所示.
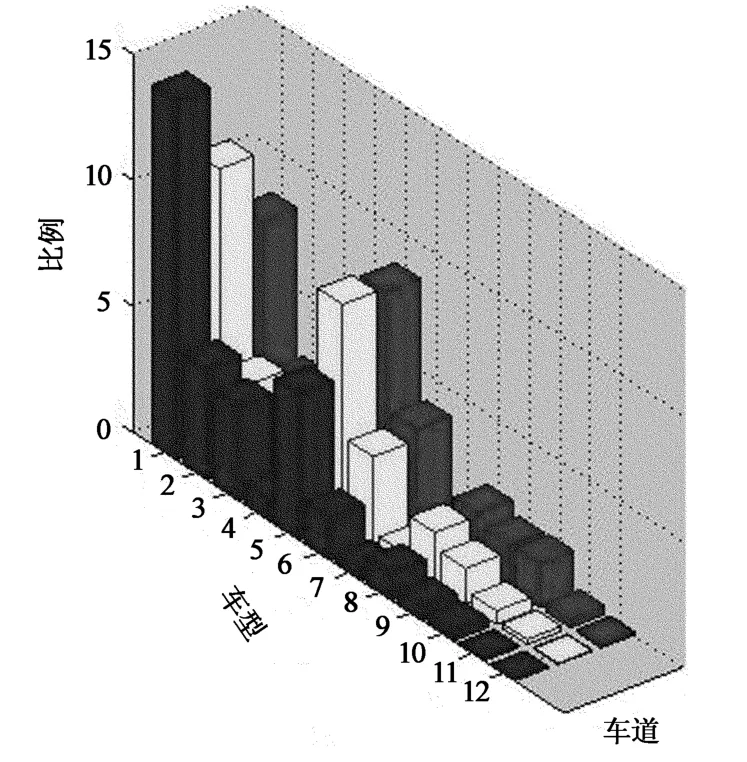
图1 24hC1~C12车型车道比例Fig.1 Ratio of from C1to C12vehicle models in 24hours
1.2.3 车重分析
限于文章篇幅,仅对C1车型,9:00~10:00在不同车道下的车重数据进行分析.通过桥梁动态测试仪,利用车桥耦合程序对车辆的实际车重进行识别,结合分类后的车型进行数据的筛选.通过K-S检验法,将统计所得结果,对常见的几类分布函数进行判别,结果如图2~图3所示.从上述数据可知C1车型的车重在各车道下服从极值I型分布.
1.3 随机车流模拟
通过Matlab软件编写出随机车流程序分析并进行抽样,即可获得如图4所示随机车流模拟图.图4中不同标志代表不同车型,x坐标表示纵向位置,y坐标表示车道,z坐标表示车重,每点上的数值表示车速.
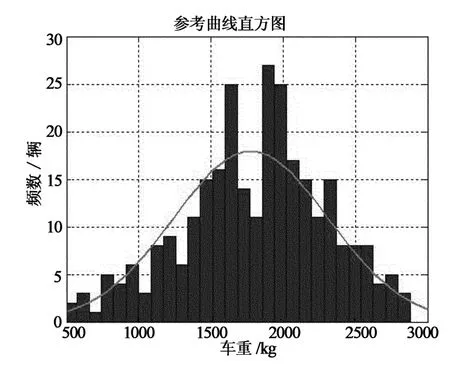
图2 C1车型在超车道时车重分析Fig.2 Weight analysis of C1vehicle in overtaking lane
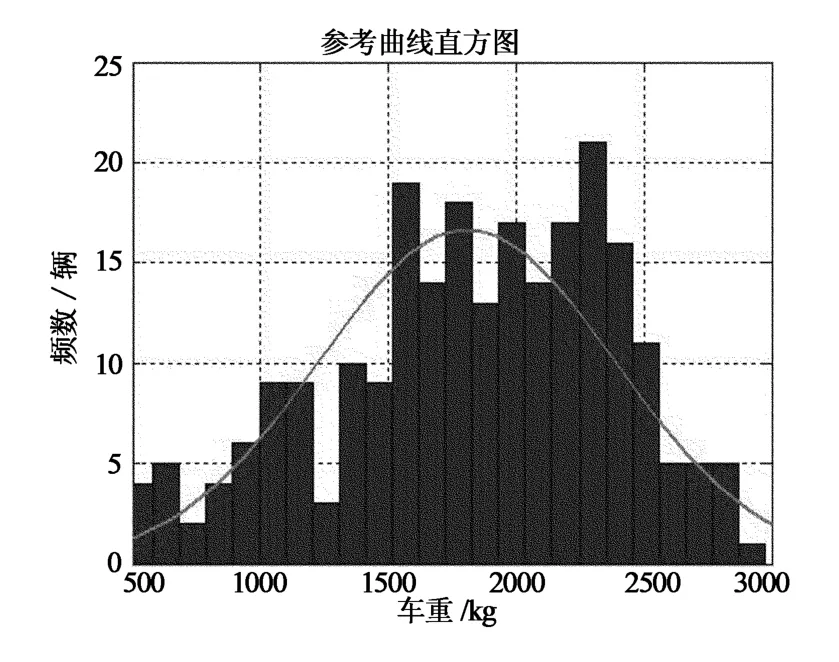
图3 C1车型在行车道一时车重分析Fig.3 Weight analysis of C1vehicle in lane one
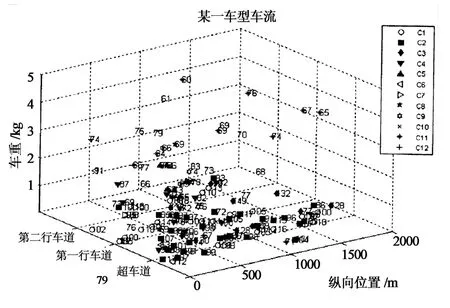
图4 随机车流模拟Fig.4 Simulation of random traffic flow
2 随机车流下最大静挠度分析
求解随机车流下最大静挠度的问题关键在于怎样获得最大静挠度下对应车辆的布载情况.主要思路为:根据响应面分析方法,拟合影响面的函数表达式,将确定随机车流布载位置的问题转化为求对应函数表达式的最大值问题.下面以斜拉桥为例,详细说明过程.
2.1 有限元软件建模及影响面求解
本文选取某斜拉桥为研究对象,该桥为斜拉桥,全长840m(210m+420m+210m).
采用机动法进行影响面的求解,选择跨中截面点作为研究对象,将包含位置节点在内的单元作为强迫应变盒[10],对单元上的4个节点各施加竖直向上的单位强制位移,为了突出竖向变形形状,将显示比例调整到25倍,形成了如图6所示曲面图形.由图6可知,竖向最大位移为1.025m,出现在强制位移处,由于受到桥梁支座约束的影响,最小位移为-0.177m,出现在边跨跨中位置.将相应强迫应变产生的节点反力反向施加在对应的节点上,形成了如图7所示变形曲面.对比两图的形状以及数据可知,变形形状十分接近,最大值相差0.001,仅为变形量的0.975%;最小值相差则完全吻合.

图6 强制位移Fig.6 Forced displacement

图7 等效荷载位移Fig.7 Equivalent load displacement
2.2 影响面的拟合
本文采用多项式拟合法进行拟合,在拟合中,其正规方程组往往是病态的,而且正规方程组系数矩阵的阶数越高,病态越严重;拟合节点分布的区间[x0,xm]偏离原点越远,病态越严重;xi(i=0,1,…,m)的数量级相差越大,病态越严重.针对上述问题,对模型数据做出以下调整:将纵、横桥向坐标进行平移处理;根据影响面的形状特点,将桥梁结构划分成(50m+23m+24 m+23m+50m)共5个区段;选择x,y均为2阶函数进行拟合.利用Matlab软件分段拟合,如图8~图13所示.拟合公式如下:

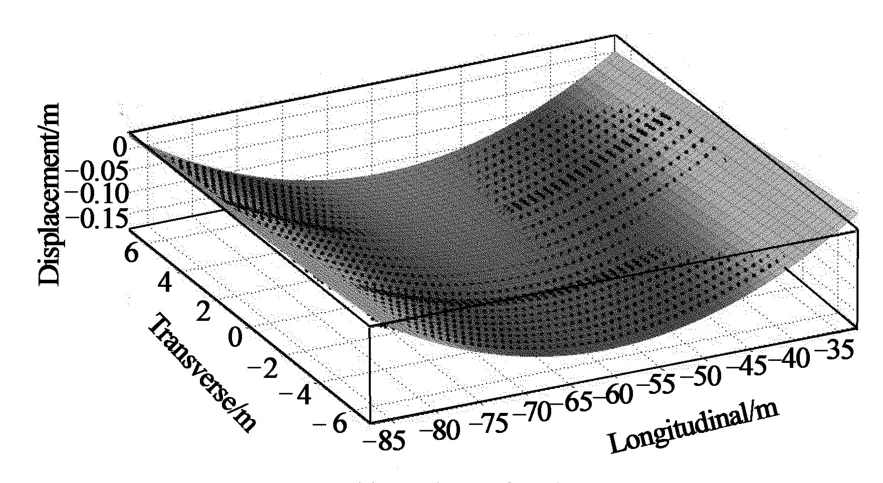
图8 第一部分拟合曲面Fig.8 The first part of the fitting surface
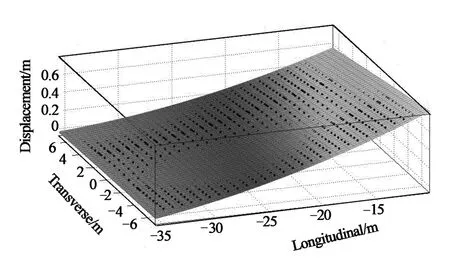
图9 第二部分拟合曲面Fig.9 The second part of the fitting surface

图10 第三部分拟合曲面Fig.10 The third part of the fitting surface
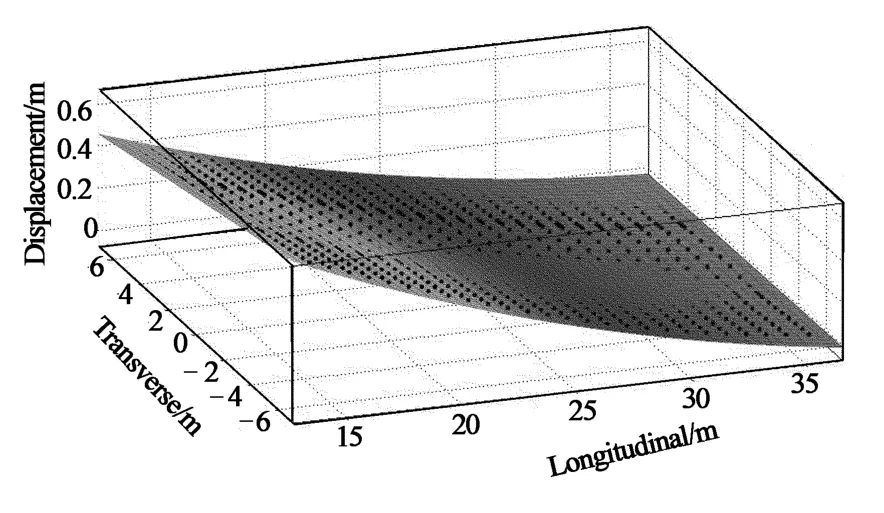
图11 第四部分拟合曲面Fig.11 The fourth part of the fitting surface
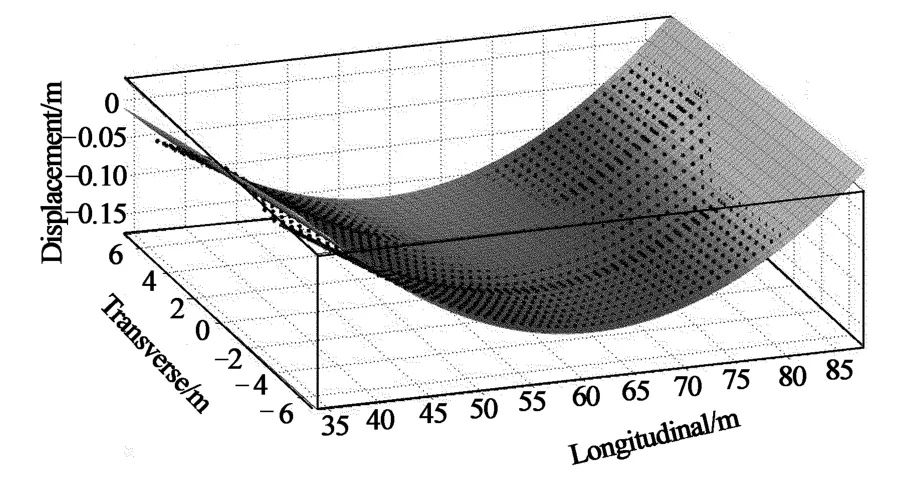
图12 第五部分拟合曲面Fig.12 The fifth part of the fitting surface

图13 分段函数图形Fig.13 Piecewise graph
由图13可知,桥面节点与拟合后曲面吻合较好,由确定系数可知,所有的拟合曲面都大于0.96,部分曲面甚至达到0.99.所以认为拟合效果能够满足计算精度的要求.
2.3 最大静挠度求解
通过上述拟合处理获得影响面表达式,布载位置的确定就转变为函数求解最大值的问题,从而使得复杂的问题简单明了.具体表达式的推导如下:
1)t时刻,第i辆车的第j轮对应的f(x,y)值表达如下:
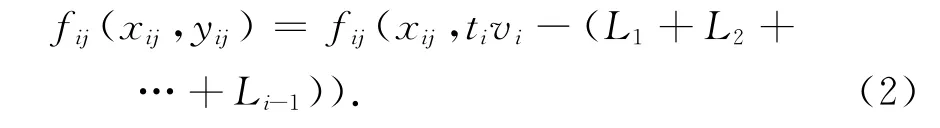
式中:Li为第i+1辆车与第i辆车之间的间距.
2)t时刻,第i辆车对影响面点的位移效应值如下式:
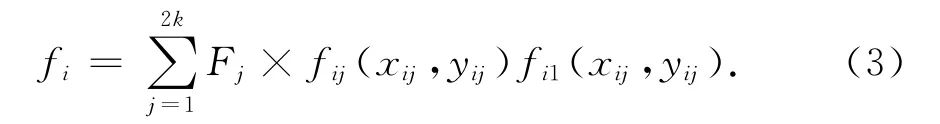
式中:k为i车的车轴数;Fj为第i辆车对应的轮重.Fj通过随机生成的车重数据,按照车重对车轴的分配比率分配到各个轴,然后将轴重平均值赋予对应位置的轮胎重力Fj.
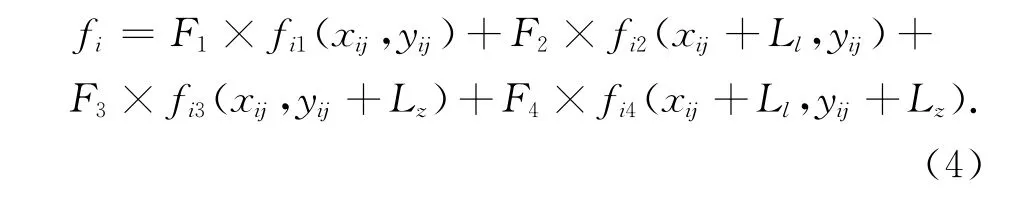
式中:Ll为车轮间距;Lz为车轴间距;F1=F2,F3=F4.t时刻,桥梁某车道上车辆对影响面点的效应之和为:

考虑到实际桥梁结构上存在车辆多向行驶的问题,因此需要对式(5)进行调整,当某一车道上车辆往顺桥向行驶时;当车辆为逆桥向行驶时.这样就可解决桥梁结构上双向行驶的问题,而且不受车道数的影响,可以逐个累加.其中:S为桥梁跨径,vi为第i辆车的速度,t时刻,桥梁上车辆对影响面点的效应之和为:
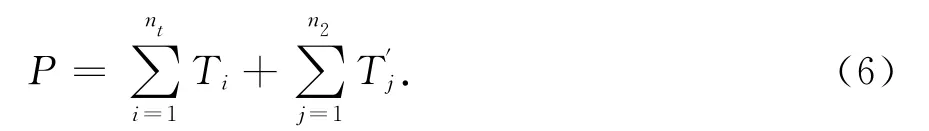
通过Matlab对P值进行循环计算,计算步长Δt=0.1s,然后对所求的P值进行筛选,获得Pmax.
3 随机车流下的车 -桥耦合振动分析程序实现
本文考虑随机车流中车辆数较多,如果所有车辆均模拟成三维车辆模型,程序的计算过程及计算难度会大大增加.为简化,计算过程分两步:首先得到车流样本中各类型车辆各自单独作用下与桥梁耦合振动的接触力;然后在随机车流桥梁振动分析时,将各自振动接触力代替各类型车辆作用在桥上.鉴于篇幅原因,下面仅以重为20t的双轴货车(第三类型)为例,介绍得到单一车辆作用下与桥梁耦合振动的接触力时程的计算过程.
3.1 单一车辆模型及其运动方程
采用7自由度两轴汽车的空间整车模型模拟20 t的大型双轴货车(第三类型),自由度包括车体的竖向位移、点头及翻滚转动,前后车轴的竖向位移及翻滚转动.该车辆模型虽然为最简单的整车模型,却能全面地分析车辆与桥梁的耦合振动特性,能比较真实地模拟实际车辆的动力特性.图14所示为整车模型的正视图和侧视图.
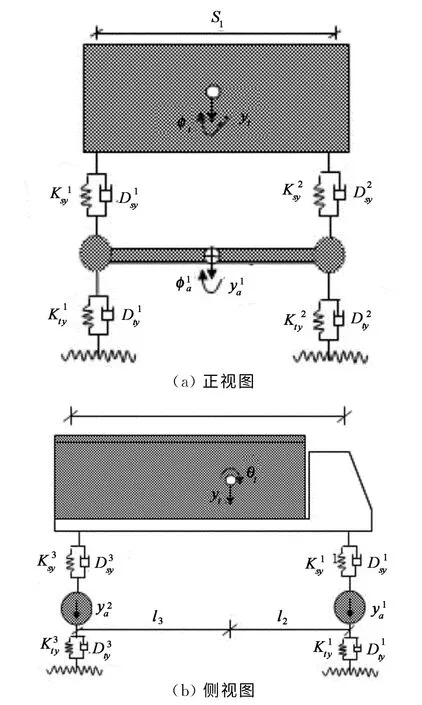
图14 整车模型Fig.14 Vehicle model
根据文献[1]可知,该车辆模型的运动微分方程矩阵形式为:
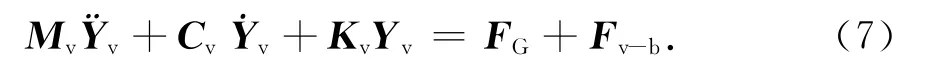
式中:Mv,Cv和Kv分别为车辆的质量矩阵、阻尼矩阵和刚度矩阵;Yv为车辆的位移向量;FG为车辆的重力向量;Fv-b为车轮与路面接触面作用于车轮的反力.
3.2 桥梁运动方程
根据文献[1]可知,桥梁的运动方程可以表示为:
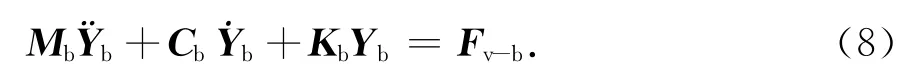
式中:Mb,Cb和Kb分别表示桥梁的质量矩阵、阻尼矩阵和刚度矩阵;Yb表示桥梁全部自由度的位移向量;˙Yb和¨Yb分别表示Yb关于时间的一阶和二阶导数;Fv-b是作用于桥梁的所有外力向量.
一般将路面的不平度作为空间频率函数,视为零均值的平稳随机过程[8-9].通过傅立叶变换,由此谱密度函数应用三角级数模拟得到路面不平度函数[1]:

式中:Gq(n)=Gq(n0)n20/n2,n为空间频率,n0=0.1(1/m)是标准空间频率,Gq(n0)为路面不平度系数;θi为0~2π之间均匀分布的随机数.
3.3 单一车辆作用下桥梁振动响应分析
以第三类Ⅵ型为例,总重为20t的双轴货车距离桥头15m 以速度10m/s行驶通过该桥.通过车桥耦合程序,得到车辆通过桥梁时桥梁的振动响应.
由图15可知,车辆上桥后行驶在边跨位置时,跨中位移仅出现较小的波动.15s之后逐渐增加.在22.88s时刻,即车辆行驶在跨中位置时位移达到最大值-4.09cm,随着车辆离开跨中位置,竖向位移逐渐减小,44s位置车辆离开桥梁,跨中位移仍然在小范围内发生波动.
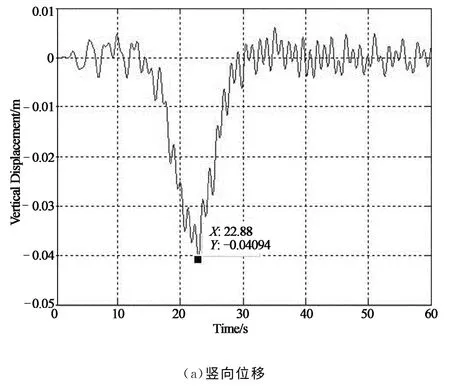

图15 单车作用下车-桥耦合系统振动响应Fig.15 Vibration response of vehicle-bridge coupled system
跨中截面竖向加速度则是随着车辆上桥逐渐增大.行驶到22.92s时刻,竖向加速度达到最大值0.131 7m/s2.随着车辆离开跨中位置,加速度逐渐减小.计算得后轴重为12.1t,在考虑车桥耦合作用下,后轴的接触力如图15(c)所示,最大值出现在30.02s位置,达到12.83t.
3.4 随机车流作用下桥梁振动响应分析
如图15(c)所示,基于车桥耦合程序可得考虑单车-桥耦合振动效应后的单车作用在桥梁时车轴接触力时程数据值.在随机车流桥梁振动分析时,为简化计算过程,可将各类车单独作用在桥上时所得时程接触力数据值代替三维车辆模型直接作用在桥梁结构上[9].为与单车作用下桥梁振动对比研究,车流总车重约为20t,则车流样本作用下的振动响应如图16所示.
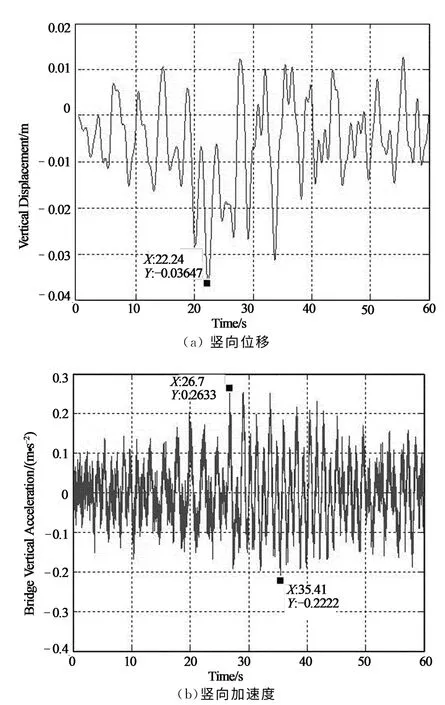
图16 车流样本作用下桥梁振动响应Fig.16 Vibration response of the bridge under the traffic loads
跨中竖向位移在1~10s期间有较明显的增加趋势,由于受到的是车流影响,竖向位移与单一车辆相比规律性不明显.在考虑60s内的竖向位移时,最大位移为3.647cm,发生在22.24s位置;对比单车作用下最大位移值可知,车流作用下最大位移值要小,这可能是由于车流中部分车辆作用在跨中截面的负弯矩区域,使跨中位置产生了反向位移,从而减小了车流作用下跨中最大位移.
4 随机车流作用下桥梁的冲击系数统计分析
本文通过大量的计算获得一系列分散数据,再对数据进行统计分析从而获得对应的分布函数和统计参数.借助Matlab工作平台,采用K-S检验法对数据进行常规的5种分布函数检验.若分布函数与经验函数差值的绝对值的最大值小于临界值,则表示假设成立.由表2可知,经过K-S检验得出其服从极值Ⅰ型分布和正态分布,但是比较观测值和临界值可以发现,数据与极值Ⅰ型分布的吻合程度要高于正态分布(如图17所示),所以认为冲击系数服从极值Ⅰ型分布.
本文根据获得的分布函数求解0.9 分位数[10]的冲击系数值为0.161 5.与按照04规范求解得到的冲击系数值0.149相比,随机车流作用下所得冲击系数要大8.38%,虽然04 规范与本文计算值有差别,但若从工程设计角度出发,04规范还是可运用于斜拉桥的设计中.

表2 冲击系数检验Tab.2 Test of impact factor

图17 冲击系数拟合图Fig.17 Fitted curve of impact factor
5 结 论
现有冲击系数的研究较少考虑到交通车流的随机特征,这与实桥上作用的交通荷载不符.因此,本文提出了简便且实用的随机车流作用下桥梁结构冲击系数计算方法,结果表明:
1)基于响应面分析方法,提出了随机车流作用下桥梁结构最大静挠度的计算方法,算例表明该方法具有足够的计算精度,满足计算精度的要求.
2)根据随机车流中各类车型的三维模型和已编制的车-桥耦合振动分析程序,提出了随机车流作用下桥梁结构冲击系数的计算方法,算例表明所提出的方法能有效地计算随机车流下桥梁的冲击系数.
3)冲击系数统计分析表明,随机车流作用下冲击系数服从极值Ⅰ型分布,统计值比04规范求解所得的0.149大8.38%.
[1]殷新锋.汽车荷载作用下梁式桥与斜拉桥的动态响应分析[D].长沙:湖南大学土木工程学院,2010:20-30.
YIN Xin-feng.Dynamic response analysis of beam bridge and cable-stayed bridge under vehicle loads[D].Changsha:College of Civil Engineering,Hunan University,2010:20-30.(In Chinese)
[2]夏禾.车辆与结构动力相互作用[M].北京:科学出版社,2005:154-164.
XIA He.Vehicle-structure interaction[M].Beijing:Science Press,2005:154-164.(In Chinese)
[3]DENG L,CAI C S.Development of dynamic impact factor for performance evaluation of existing multi-girder concrete bridges[J].Engineering Structures,2010,32(1):21-31.
[4]DENG L,CAI C S,BARBATO M.Reliability-based dynamic load allowance for capacity rating of pre-stressed concrete girder bridge[J].Journal of Bridge Engineering,2011,16(6):872-880.
[5]姚成钊.考虑桥面不平顺影响的公路车流-桥梁耦合振动分析研究[D].长沙:中南大学土木工程学院,2008:40-50.
YAO Cheng-zhao.Consider deck irregularity affecting road traffic-bridge coupled vibration analysis[D].Changsha:Col-lege of Civil Engineering,Central South University,2008:40-50.(In Chinese)
[6]韩万水,陈艾荣.随机车流下的风-汽车-桥梁系统空间耦合振动研究[J].土木工程学报,2008,41(9):97-102.
HAN Wan-shui,CHEN Ai-rong.Three dimensional coupling vibration of wind-vehicle-bridge systems under random traffic flow[J].China Civil Engineering Journal,2008,41(9):97-102.(In Chinese)
[7]彭献,殷新锋,方志.变速车辆与桥梁的耦合振动及其TMD控制[J].湖南大学学报:自然科学版,2006,33(5):61-66.
PENG Xian,YIN Xin-feng,FANG Zhi.Vibration and TMD control of coupled system of girder bridge and vehicle with variable speeds[J].Journal of Hunan University :Natural Sciences,2006,33(5):61-66.(In Chinese)
[8]周勇军,赵煜,贺全海,等.刚构-连续组合桥梁冲击系数多因素灵敏度分析[J].振动与冲击,2012,31(3):97-101.
ZHOU Yong-jun,ZHAO Yu,HE Quan-hai,etal.Muti-parameters sensitivity analysis of impact factors for rigid-continuous combined bridge[J].Journal of Vibration and Shock,2012,31(3):97-101.(In Chinese)
[9]CHEN Su-ren.Dynamic performance of bridges and vehicles under strong wind[D].Baton Rouge:Louisiana State University,2004:60-74.
[10]肖汝诚.空间结构内力影响面的有限元计算方法[J].计算结构力学及其应用,1990(4):56-63.
XIAO Ru-cheng.Spatial structure of internal force influence surface of the finite element method[J].Computational Structural Mechanics and Applications,1990(4):56-63.(In Chinese)
