基于加权复杂网络的公路网等级结构划分*

邓亚娟 王欢 杜若 胡绍荣

(1.长安大学 公路学院 交通工程研究所，陕西 西安710064;2.陕西省 交通运输厅，陕西 西安710075)

公路网等级划分是公路网规划的重要内容，对未来年需要进行等级提升的公路网来说，得到一个与实际需求相匹配的等级结构划分是路网规划的重要步骤.公路网等级结构是指公路网中不同技术等级公路所占比例，从量上反映公路网的等级结构，就是确定各等级公路里程所占比重.公路网的等级结构决定了公路网的运输能力，公路网的等级结构等级越高，对交通需求的满足程度就越高.公路网等级结构按照其技术等级分为一级、二级、三级、四级以及等外公路，按照行政等级分为国道、省道、县道和乡道.现状路网等级划分主要有以网络建设成本最小为目标的单目标规划模型［1］以及以可达性、连通性［2］、公平性［3］和网络脆弱性等最优［4］的多目标规划模型，在大力提倡低碳交通的背景下，Bruno 等［5］提出区域公路网等级优化是使用者友好型，是以公平、网络稳定性和能源消耗少为目标，建立的多目标规划模型.已有的目标规划模型对于发展相对成熟的公路网等级优化效果较好，但不适用于公路网发展较为薄弱的地区，且应用时需要针对特定区域、特定问题添加合理目标和约束条件;目标规划法更多的以通行能力、周转量以及服务水平等为约束，规划结果不能体现公路网等级与路网结构的关系;除此之外，目标规划法只能得到各等级公路里程总量，而不同等级公路在路网中的具体位置需要结合四阶段法进行，调查工作量大且计算过程较为复杂.

以复杂网络理论为基础的公路网结构研究，可从另外一个角度解析公路网所具有的结构特征，复杂网络理论最初应用在社会网络和计算机网络分析领域，20世纪90年代开始逐步应用于交通运输领域，研究主要集中在城市道路及公共交通网络领域.Jiang 等［6］针对特定城市道路网络应用复杂网络理论研究其拓扑结构，Barrat 等［7］对复杂网络的权重特征进行了相关分析.邓亚娟等［8］将复杂网络理论引入公路网研究领域，基于复杂网络分析指标对公路网特征进行了研究.文章将对公路网进行加权对偶拓扑转换，以复杂网络指标分析为中心思想，进行公路网等级划分.具体研究内容为:以流量及路线贯穿性作为权重对拓扑节点进行加权处理，建立公路网加权邻接矩阵，并在此基础上计算应用节点重要度、紧密度、介数3 个复杂网络指标，以其作为拓扑节点的重要性指标，最后采用模糊聚类对所有拓扑节点进行类别划分.这样不仅可以得出各等级公路的里程，还可以得到各级公路在整个路网中的具体位置，对未来年公路网改建扩建具有现实参考意义.方法的使用前提是现状公路网络结构基本完整，后期规划主要针对交通需求对现状路网等级结构进行进一步完善和配置，即适用于路网较为成熟的区域.

1 对偶网络拓扑图的建立

网络结构分析最关键的问题是利用合理规则拓扑处理现实中的交通网络.目前常用的网络拓扑方法主要有:①原有拓扑，即以边为拓扑结构的边，交叉口为节点［9］;②对偶拓扑，以道路编号或者路名为节点，即相同的路名可用一个节点代替，交叉口为节点之间的连线［9］;③加权对偶拓扑，以道路编号或者路名为节点，即相同的路名可用一个节点代替，交叉口为节点之间的连线，但连线之间的关系并不仅仅是邻接或不邻接的简单几何关系，而是从网络本身结构出发，反映连线之间链接的紧密性.以图1(a)所示公路网为例，基于原有拓扑方法所形成的拓扑图如图1(b)所示，基于对偶拓扑方法所形成的拓扑图如图1(c)所示，基于加权对偶拓扑方法所形成的拓扑图如图1(d)所示.由图1(d)可以明显看出，节点1、2 之间的联系最为紧密，其次是节点2、3，节点4、5 之间的联系最为薄弱.

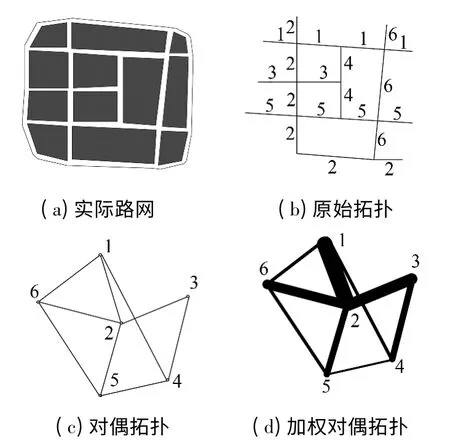
图1 公路网拓扑结构Fig.1 Highway network topology structure

现有公路网络结构分析基本沿用广义网络拓扑分析方法，该方法保留了网络原有形态，网络拓扑以路段为基础，网络评价指标集中于β 指数、α 指数和γ 指数;而在利用对偶方法得出的复杂网络拓扑结构中，网络拓扑以线路(路名)为基础，节点之间的连线能够明确表示线路之间的相互关系、线路在整个网络中的重要程度以及网络的局部和全局效率;加权对偶拓扑还可进一步描述节点之间联系的紧密程度，在同等度数条件下描述节点在现实意义中的重要程度等.普通对偶拓扑虽然可以实现线路与节点之间的相互转化，使得线路在整个网络中的重要程度及线路之间的识别关系变得简单，但只是将整个路网作为一般的网络分析其结构特征，忽略了公路网本身特性及其功能属性，文中提出的加权对偶拓扑是在网络对偶拓扑的基础上考虑了公路网本身特性，即交通流量与路线贯穿度.将这两个因子作为权重加载到路网上，有针对性地挖掘出基于复杂网络的公路网结构特征.有助于分析实际网络的交通运行特征.

在拓扑抽象过程中须遵循以下规则:①在路网评价中，评价对象多为道路，针对道路里程较短贯穿程度强度较弱的道路，在网络拓扑过程中需将道路名称相同的路段用同一节点来表示;②部分道路长度过长，甚至跨越几个行政分区，且在不同分区内路段流量分布不均匀，道路重要程度有所差异，例如普通公路网中的国道，在网络拓扑过程中针对这类道路需将道路在同一区域且流量分布较为一致的路段用同一个节点表示;③由于高速公路和铁路具有较强的区域穿越性，与其他道路的连接性不明显，在区域公路网分析中暂不考虑;④在拓扑过程中删除孤立路段;⑤在拓扑过程中对于等级较低的县乡道路，将多条邻近线路整合为一条线路，后期考虑将其打通等措施以提高其等级;⑥拓扑后的复杂网络节点之间的连线表示实际路网中各线路之间的链接关系;⑦由于研究集中在各线路之间的相互关系以及在路网中的重要程度，因此拓扑过程中仅考虑线路之间相互链接的逻辑关系，不考虑线路以及线路之间连接线的实际长度.

2 加权结构特征指标计算

为了计算得到判断线路重要性的复杂网络指标，首先应建立对应的加权邻接矩阵.邻接矩阵是表示两顶点之间是否连接的矩阵，而加权邻接矩阵是表示顶点之间联系紧密程度的矩阵，可以用来确定网络中任意两点之间是否连接及连接的紧密程度.一般地，权重越大，节点之间联系越密切，对于路网来说，其对偶拓扑网络连线权重越大，对应原始网络的节点就越重要，即形成该节点的道路网流量较大、人口相对较为密集，相邻路线之间的交通转换量随之增大.本节研究重点即为在原始拓扑图及对偶拓扑点权重已知的基础上计算评价路线重要程度的指标值，根据该指标值为后期规划提供参考.

2.1 加权邻接矩阵构建

2.1.1 确定节点权重

基于复杂网络的公路网等级结构划分实际上是将对偶拓扑节点进行分类，计算初始邻接矩阵的目的是为将来计算节点度、紧密度及介数指标做准备，但初始邻接矩阵只是针对网络自身结构进行分析，并未结合公路网本身的交通特性进行分析探讨，缺乏针对性.引入权重概念，不仅可以得出网络结构构成特点，而且能够挖掘路网本身所具有的交通特性.一般地，道路等级越高，流量越大，贯穿性也越强，因此笔者以规划年流量预测值和路线贯穿度作为对偶拓扑网络的节点权重加载于网络.为了避免量纲及效用不均等问题，文中流量、贯穿度值均取标准化后的值，即均为0 ～1 的无量纲数.其中，路网贯穿度是指公路路线所穿越的市、县、乡规划年人口预测值的加权和，根据路线贯穿的各市、县、乡人口总量给出各自权重值，求和即可得到各对偶拓扑节点贯穿度值，然后结合流量值计算各节点的权重值.具体计算公式为

式中:ωi为节点i 的权重值;为第i 个节点流量系数;2为第i 个节点贯穿度系数;ai1为第i 个节点标准化后的流量指标值，为规划年该节点的标准当量小车预测值与路网全部拓扑节点最大标准当量小车预测值的比值;ai2为第i 个节点贯穿度值，为其贯穿的所有市、县、乡的人口权重之和，其中各市、县、乡的人口权重值为该市、县或乡的人口预测值与研究区域内最大行政区人口数量预测值之比，即在路网的角度上分析各路线本身特征;其中可由变异系数法计算得到，

变异系数法即利用各项指标所包含的信息，计算得到指标权重，是一种客观赋权的方法，该方法本身可以消除各项评价指标量纲不同产生的影响.其基本思想是:在评价指标体系中，指标取值差异越大，其对分析对象的区分度越明显，说明该指标区分各评价对象的能力强，因而应给该指标较大的权数;反之，如果被评价对象在某项指标上的数值差异较小，说明该指标在评价中分辨信息能力较弱，因而应给该指标较小的权数.

各项指标的变异系数公式为

式中:νj为第j 项指标的变异系数;也称为标准差系数;σj为网络中所有拓扑节点第j 项指标的标准差;为网络中所有拓扑节点第j 项指标的平均数，j =1，2 分别表示标准化处理后的流量与贯穿度.文章所使用的流量及贯穿度指标均为标准化后的值，为无量纲指标.

各指标的权重系数公式为

2.1.2 建立加权邻接矩阵

根据现状路网建立初始邻接矩阵M1，即路线连接取1，不连接取0，在初始邻接矩阵的基础上构建加权邻接矩阵，需要求得两点之间连杆的权重，相当于求解两点之间吸引强度的大小，吸引强度越大，连杆权重值越大，反之，连杆权重值越小，这里采用重力模型构建加权邻接矩阵，具体计算公式为

式中:ωij为加权邻接矩阵中第i 行与第j 列相交位置的权重值;ωi为节点i 的权重值;ωj为节点j 的权重值;其中，节点i 与节点j 邻接，γ 为两节点之间的距离.

公路等级与流量、贯穿度相关，在式(4)中分母部分完全体现这一思想.且路网经对偶拓扑处理以后，拓扑节点之间的连杆在现实路网以交叉口的形式体现，节点之间不存在距离对吸引强度的影响，即γ 对权重影响不大.为简化计算取γ 值为常数1，式(4)转换为

综上所述，建立加权邻接矩阵步骤包括:①在公路网原始拓扑图的基础上，建立初始邻接矩阵M1;②根据式(1)- (5)计算拓扑节点连杆权重ωij，并用ωij替换掉初始邻接矩阵M1中值为1 的元素得到矩阵M2;③对矩阵M2求倒得到加权邻接矩阵M，为后续最短路相关计算提供基础数据.以图1所示网络为例，加权邻接矩阵的形成过程见图2.

图2 加权邻接矩阵形成过程Fig.2 Formation of weighted adjacency matrix

2.2 特征指标计算

现有的关于网络特征指标的研究主要有以下两种类型:①社会网络，特征指标为节点度、紧密度、介数;②病毒传播网络，特征指标为节点度、特征向量、紧密度、介数.前者用来研究个体在社会网络中的重要性，后者则主要用来分析计算机病毒传播网络、信息传播网络等具有传播行为的网络.对公路网进行等级划分，前提是判断各路线的重要程度，因此文中选择复杂网络指标对路网各路线重要性进行判别分析，可以看出文章研究的目的与社会网络相似，也是研究个体(路线)在网络中的重要性，因此选择节点度、紧密度及介数这3 个指标进行分析计算.

度指标，是研究复杂网络拓扑结构的基本参数，用于描述在静态网络中节点所产生的直接影响力，度指标反映的是一个节点对于网络中其他节点的直接影响力.针对公路网，度指标反应了该路线与周围路网的连接能力.一般地，节点度指标越大，该路线与周围路网联系越紧密，且所连接的路线等级越高，理论认为该路线等级也需要相应的提高才可以满足交通需求.

紧密度指标，用于刻画网络中的节点通过网络到达其他节点的难易程度，反映的是节点通过网络对其他节点施加影响的能力.针对公路网，紧密度指标越大，该路线到达其他各路线的最短路径之和越小，对道路使用者而言，该路线的效用值越大，对路网的贡献越大.道路使用者更倾向于选择该路线以达到出行目的，进一步说明紧密度大的路线在整个路网中重要性也大.

介数指标［10-11］，刻画了网络中的节点对于信息流动的影响力.介数指标中引进了信息流动的概念，在使用最短路径算法的网络中，介数指标刻画了信息流经给定节点的可能性，任一节点的介数指标均会随着经过该节点的信息流的增加而增大，利用介数指标可以确定信息负载繁重的网络节点.针对公路网，节点的介数越大，该路线负荷的流量越大，路网中任意两条路之间的最短路径经过该路线的次数越多，介数指标更能反映该路线在整个路网中的重要程度.

指标计算公式如下.

(1)节点重要度

式中，Ni表示与节点i 邻接的节点集合，ωij表示与节点i 连接的连线权重.

(2)紧密度

式中，d(i，k)为节点i 到k 的最短路径.

(3)介数指标

式中，pjik为节点j 到节点k 之间通过节点i 的最短路径数量，pjk为节点j 到节点k 之间的最短路径数量.

根据式(6)对矩阵M2在Excel 中直接对各行进行求和计算得到节点重要度指标，再根据式(7)与式(8)通过Matlab 编程对矩阵M 进行紧密度指标与介数指标的计算，最终得到一个n × 3 阶矩阵(n表示节点数).

3 网络节点筛选

公路网等级划分是在路网规划总里程的基础上实现的，因此划分出的各等级公路里程之和需要与规划年公路网总里程预测值相匹配.基于复杂网络的公路网等级划分法是一种适用于现状路网总体结构较为完整、后期规划无需新建道路只需要对现状路网中未来年交通需求较大的路线进行等级提升的规划方法，因此需要以路网总里程为控制标准，按照重要性由大到小的顺序选取m 个节点，使得这m 个节点所代表的路线里程之和与公路网未来年预测总里程相等，这m 个节点所代表的路线即为规划年需要根据级别划分提高等级的m 条路线.

文章综合考虑每个节点的节点度、紧密度及介数指标，按照节点综合指标值δi从大到小的顺序依次选取与规划年路网总里程匹配的前m 个节点.节点综合指标δi的计算方法为

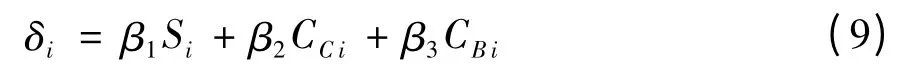
式中，δi为第i 个节点的综合指标权重值，β1、β2、β3分别为节点度、紧密度、介数3 个指标的权重系数，其计算方法仍然采用变异系数法;Si为节点i 的节点度值，CCi为节点i 的紧密度值，CBi为节点i 的介数值，文中加权邻接矩阵中的权重值是标准化后的无量纲指标，因此所计算得到的节点度、紧密度、介数指标均为0 ～1 的无量纲指标.

以规划年路网总里程L 为控制标准，根据各节点综合权重指标值δi的大小顺序进行节点筛选，使得选出的节点所代表的路线里程li之和与规划年路网总里程L 相等，这样做的目的是在满足里程匹配条件下使所选的拓扑节点为重要度最大的路线.

4 等级结构划分

用模糊聚类法将上节所选出的节点进行聚类分析，按照现有公路网等级划分标准将其分为4 类，将每类中包含的节点所代表的路线里程相加即可得到各等级公路里程.具体流程为:矩阵U-模糊相似矩阵R-模糊等价矩阵R*-等价布尔矩阵U*-等级划分.

4.1 模糊等价矩阵的建立

为了根据复杂网络指标进行类别划分，首先需要根据指标矩阵建立模糊相似矩阵［12-14］，即标出衡量被分类的对象之间相似程度的统计量rij(i = 1，2，…，n;j = 1，2，…，n).确定相似系数rij的方法有相似系数法、距离法以及主观评价法，其中相似系数法分为数量积法、夹角余弦法、相关系数法、指数相似系数法、最大最小法、算术平均最小法以及几何平均最小法等.距离法分为海明距离、欧几里德距离、切比雪夫距离等.实际应用中需要根据问题的性质来决定具体使用什么方法.其中，距离系数是用来描述Q 型聚类即区分变量的统计量，相似系数法是用来描述R 型聚类即区分样本的统计量.对公路网进行等级划分属于R 型聚类，相似系数法中的相关系数法适用于原始数据矩阵的不同行来自不同母体的情况，指数相似系数法适用于原始数据矩阵的不同列来自不同母体的情况，具有一定的局限性.一般地，多采用夹角余弦法来计算节点之间的相似程度，得到模糊相似矩阵R，在数据挖掘领域中，用夹角余弦法来衡量集群内部的凝聚力.文中研究的核心结论为通过复杂网络指标值挖掘路网特征，将所有拓扑节点进行聚类分析，相似程度高的被划分至同一集群，与夹角余弦适用性吻合性强，因此采用夹角余弦法计算两拓扑节点的相似程度.算法为

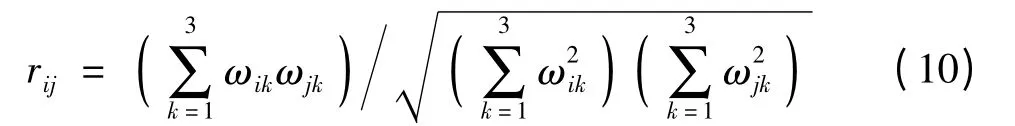
式中，rij为第i 条道路与第j 条道路的模糊相容关系，ωik为第i 条道路第k 个指标的取值，ωjk为第j条道路第k 个指标的取值，k = 1，2，3 分别表示节点度、紧密度、介数.

采用传递闭包(平方法)对矩阵R 进行转化，从模糊相似矩阵R 出发，依次求平方，R→R2→R4→…→R2l→…直至出现Rk·Rk= Rk时(模糊相似矩阵R 连续平方计算K 次就可以得到一个平方与其本身完全一致的矩阵Rk，这个矩阵Rk便是我们所需要的模糊等价矩阵，矩阵Rk具有传递性)，Rk就是所求的传递闭包矩阵即模糊等价矩阵R*.这里K 值最大为

4.2 模糊聚类阈值 的选取

得到模糊等价矩阵，就可以给定阈值，使得 对应的聚类数与规划要求的等级数匹配.具体做法如下:在得到的模糊等价矩阵R*中，rij*为矩阵模糊等价矩阵R*中的元素，依次在矩阵R*中将阈值 从大到小取值可以得到对应的等价布尔矩阵U，uij为矩阵U 中的元素，当 ＞rij*时，uij=0;当 ＜rij*时，uij=1，等价布尔矩阵U 中的元素值非0 即1，uij=1 时，说明节点i 与j 在同一个等价类中，从大到小依次取值，可以得到道路网的一个逐渐由细变粗的动态分类.当得到的类别数n =4 时对应的τ值即为满足路网等级划分的阈值，统计各等级的路线并将其里程求和即得到各级公路里程值.至此完成了对公路网的等级划分.

基于加权复杂网络的路网等级划分，可以将路网等级根据需要划分为任意个类，根据公路网自身特性需要将其划分为4 个等级.但划分为4 个类的结果是否合理还需要对聚类结果进行检验分析，笔者采用Spss 统计分析软件对聚类结果进行验证，当聚类显著性水平符合要求时认为聚类结果是合理的，可以运用到实际中.

5 实例分析

文章以某省干线公路网为例，对其2030年干线公路网进行等级结构划分.首先对该省公路网进行对偶拓扑，共对偶抽象出208 个节点.两条相连道路之间连杆的权重为两道路节点权重之积，由此可以得到一个208 ×208 的加权邻接矩阵M，由矩阵M可以算出各拓扑节点的节点度、紧密度及介数指标，得到一个208 ×3 的指标矩阵A.以2030年干线公路网规划总里程为控制标准进行节点的筛选，所选节点对应的路线即为未来年需要提升为干线公路的对象.具体做法为:根据变异系数法在矩阵A 的基础上由式(9)计算各节点的综合指标，并根据其值大小对节点进行排序筛选.由于2030年该省干线公路网规划总里程为23 000 km，以该里程值及每条道路的重要性尽可能大为控制标准.在208 个节点中筛选出191 个节点，得到一个191 ×3 的矩阵A*，对矩阵A*进行模糊聚类.经分析计算，阈值 =0.9985时可以将节点划分为4 类，即将干线公路网划分成4 个等级.经Spss 验证，结果符合显著性水平要求.表1为聚类结果，县乡道路均以编码表示.

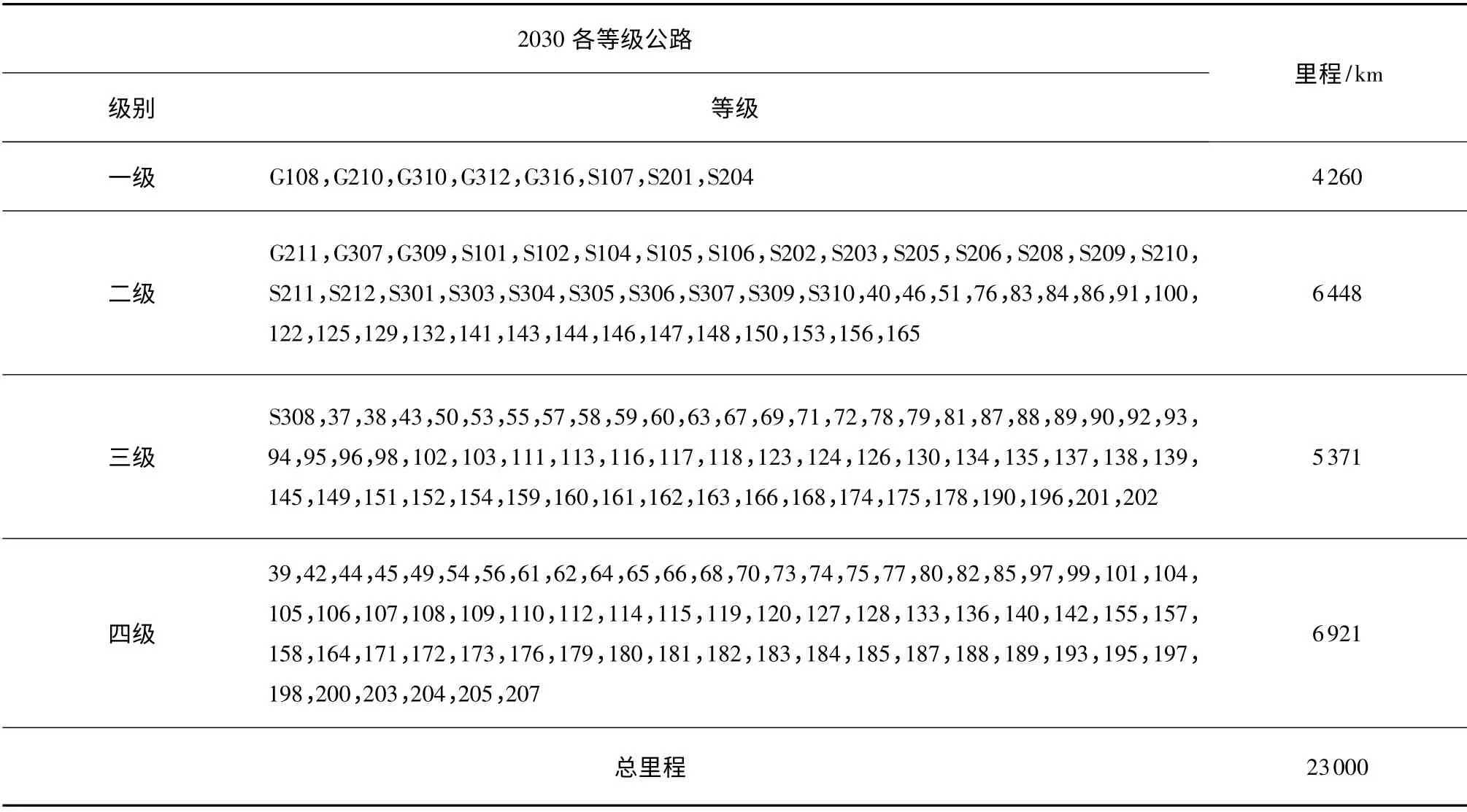
表1 某省公路网等级结构Table1 Highway network grade structure of one province

由表1可以看出，截至2030年，该省内G108、G210、G310、G312、G316、S107、S201、S204 等级结构达到一级水平.聚类结果显著性符合要求.将划分结果与传统规划方法得出的结论进行对比分析，资料［15］显示传统四阶段法得到2030年该省规划二级以上国省干线公路里程达到10000 ～16000 km，文中所采用方法得出一、二级公路里程之和达到10708 km，规划结论所得出的等级配置与传统四阶段法结论吻合，方法具有可操作性及实用性.基于加权复杂网络的方法可以用来进行其公路网等级结构划分，可以有效解决未来年道路等级提升问题，同时可以看出聚类结果符合实际情况，即越重要的道路被划分到等级越高的类中.

图3(a)为该省2030年干线公路网对偶拓扑图，经过节点筛选及等级划分得到各等级干线公路所在具体位置，图3(b)为2030年该省干线公路网等级结构划分结果.

由图3(b)可以看出，2030年各条线路都有其对应的等级，一级与二级公路里程分布较均匀，符合人民日益增长的交通需求，而且由于未来年新建道路有限，基本是在原有县乡道路的基础上进行改建、扩建来提高干线公路网总里程，采用文中提出的复杂网络法进行路网等级划分，基于各线路自身需求不仅可以得到各等级公路规划里程，而且可以得到各级公路的分布情况，对于规划年干线公路网改扩建实施具有良好的现实参考意义，使得规划年工程实践具有更好的针对性.

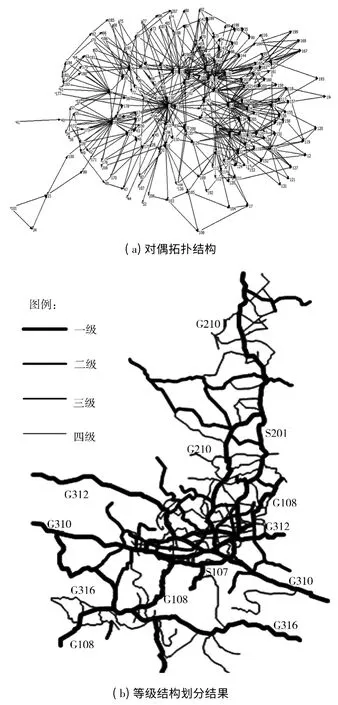
图3 某省干线公路网等级结构Fig.3 Highway network hirarchy of one province

6 结语

(1)以路段交通流量预测值及贯穿度预测值作为对偶拓扑网络的节点权重，引入重力模型的思想建立加权邻接矩阵，使得结果更加合理.经验证，计算出的节点综合指标值大小符合实际情况，即流量大贯穿性强的路线重要性大，相反重要性小的路线流量肯定不会大，其贯穿性也相对较弱.

(2)综合考虑节点重要度、紧密度及介数指标等复杂网络指标评估节点重要性，并将其作为公路网等级结构划分的基础，不仅可以体现路网交通特性在等级优化中的重要性，同时又可以得到不同等级公路的具体空间分布，可以有效解决未来年路网等级提升问题.

(3)基于模糊聚类方法，选择合理的类别划分阈值进行公路网等级结构划分，可以得到最佳的公路网等级结构配比.

［1］Janson B N，Buckets L S，Peterson B E.Network design programming of united-States highway improvements［J］.Journal of Transportation Engineering-ASCE，1991，117(4):457-478.

［2］Scaparra M P，Church R L.A GRASP and path relinking heuristic for rural road network development［J］.Journal of Heuristics，2005，11(1):89-108.

［3］Feng C M，Wu J Y J .Highway investment planning model for equity issues［J］.Journal of urban planning and development-ASCE，2003，129 (3):161-172.

［4］Chootinan P S，Wong C，Chen A.A reliability based network design problem［J］.Journal of Advanced Transportation，2005，39 (3):159-174.

［5］Bruno Santos，Antonio Antunes，Eric Miller.Multiobjective approach to long-term interurban multilevel road network planning ［J］.Journal of Transportation Engineering，2009，135(9):640-649.

［6］Jiang B，Claramunt C.A structural approach to the model generalisation of an urban street network［J］.Geoinformatica，2004，8(2):157-171.

［7］Barrat A，Barthelemy M，Pastor-Satorras R.The architecture of complex weighted networks［J］.Proc Natl Acad Sci USA，2004，101(11):3747-3752.

［8］邓亚娟，杨云峰，马荣国.基于复杂网络理论的公路网结构特征［J］.中国公路学报:自然科学版，2010，23(1):98-104.Deng Ya-juan，Yang Yun-feng，Ma Rong-guo.Highway network structure characteristics based on complex network theory ［J］.China Journal of Highway and Transport:Na-tural Science Edition，2010，23(1):98-104.

［9］于海宁，张宏莉，余翔湛.交通网络拓扑结构及特性研究综述［J］.华中科技大学学报:自然科学版，2012，40(1):274-279.Yu Hai-ning，Zhang Hong-li，Yu Xiang-zhan.Survey on transportation network topology and its properties ［J］.Huazhong Univ of Sci ＆ Tech:Natural Science Edition，2012，40(1):274-279.

［10］李金华，孙东川.复杂网络上的知识传播模型［J］.华南理工大学学报:自然科学版，2006，34(6):99-102.Li Jin-hua，Sun Dong-chuan.Knowledge propagation model in complex networks［J］.Journal of South China University of Technology:Natural Science Edition，2006，34(6):99-102.

［11］吴娇蓉，李铭，魏明.基于修正线路介数中心度的公交骨干线提取方法［J］.同济大学学报:自然科学版，2013，41(7):1009-1014.Wu Jiao-rong，Li Ming，Wei Ming.Bus main line extraction method based on modified line betweenness centrality ［J］.Journal of Tongji University:Natural Science Edition，2013，41(7):1009-1014.

［12］何小亚，刘杰.求模糊关系传递闭包的一种算法［J］.模糊系统与数学，2006，20(3):83-85.He Xiao-ya，Liu Jie.An algorithm for the transitive closure of fuzzy relations ［J］.Fuzzy Systems and Mathematics，2006，20(3):83-85.

［13］王晟.模糊聚类算法的研究与实现［D］.南京:南京理工大学计算机科学与工程学院，2006.

［14］卢秋根.模糊聚类算法的研究与实现［J］.电脑知识与技术，2008，3(9):1987-1990.Lu Qiu-gen.The research and realization of fuzzy clustering algorithm［J］.Computer Knowledge and Technology，2008，3(9):1987-1990.

［15］冯明怀.陕西省公路网规划与实践的探索［D］.西安:长安大学公路学院，2001.