永磁同步电机的分数阶无位置传感器控制*

陈思溢 皮佑国

(1.华南理工大学 自主系统与网络控制教育部重点实验室，广东 广州510640 2.华南理工大学 自动化科学与工程学院，广东 广州510640)

高性能永磁同步电机控制系统对速度和位置控制精度要求日益增高，对传感器的要求也随之提高，从而势必加大系统安装的成本.因此，永磁同步电机无位置传感器控制系统在风机、水泵等适用于位置开环或对稳态精度要求不高的领域内获得了愈发广泛的应用.如何在不对电机转速与转子位置进行直接测量的基础上，提高系统的控制与观测精度，已成为永磁同步电机无位置传感器控制领域内亟待解决的问题.

目前，除了采用高频信号注入和卡尔曼滤波［1-3］等需要增加系统外设或系统计算复杂程度的方法来提高系统控制与观测精度外，滑模观测技术以其对系统参数时变和外部扰动的强鲁棒性，为无位置传感器系统的高性能控制提供了一条有效的途径.其中，滑模观测技术主要可分为以下几类:采用高阶滑模观测器算法［4］;加入自适应算法，实现动态调节滑模观测器［5］;利用智能控制算法调节滑模观测器参数［6-8］.虽然采用上述方法能在一定程度上提高无位置传感器控制系统的控制与观测精度，但它们均未对低速或零速状态下的系统控制与观测效果进行分析，而这正是无位置传感器控制系统的研究难点所在.因此，上述方法均具有一定的局限性.

文中采用他控启动和自控运行的分段控制策略，即在转子定位以后，给电机定子一个旋转磁场使电机启动，启动后滑模观测器不断对电机的电流和转速进行观测，待电机启动到其电流电压满足预测计算时再切换到自控方式运行.同时，为了提高无位置传感器的控制与观测精度，减小系统控制方式由他控向自控切换过程中所产生的抖振，算法中永磁同步电机分数阶数学模型与分数阶滑模观测器的引入，为其提供了一种新的解决思路.

首先给出了永磁同步电机的分数阶数学模型;然后在此基础上提出基于分数阶滑模观测器的转子位置与转速的估计方法以及相应的分数阶Lyapunov稳定性证明方法，同时也讨论了分数阶滑模观测器参数的整定方法;最后给出了仿真分析及原型实验.实验结果证明，文中提出的控制策略具有较高的综合控制性能.

1 永磁同步电机分数阶数学模型

永磁同步电机在两相静止α，β 坐标系下的定子电压方程为［9］

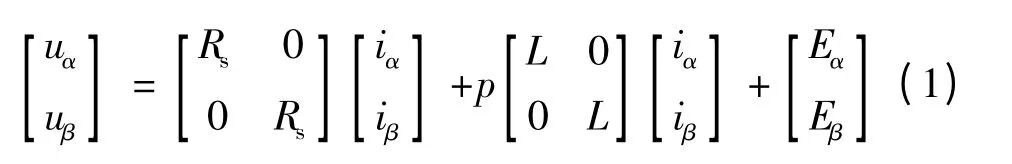
式中，uα、uβ为α，β 坐标系下的定子电压，iα、iβ为定子电流，Rs为定子电阻，L 为定子电感，p 为微分算子，Eα、Eβ为反电动势.

相应地，电磁转矩平衡方程为

式中，J 为转动惯量，Bm为摩擦系数，TL为负载转矩，TM为电磁转矩，ω 为转速.

通过采用id=0 的磁场定向控制策略，其中id为两相旋转坐标系下的直轴电流，电磁转矩平衡方程可简化为

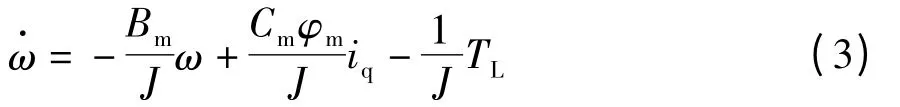
式中，φm为气隙磁通量，Cm为电机在额定磁通下的转矩系数，iq为两相旋转坐标系下的交轴电流.

考虑到实际电容和电感所具有的分数阶特性，结合文献［10］提出的永磁同步电机分数阶建模方法，给出永磁同步电机的分数阶方程表达式如下:

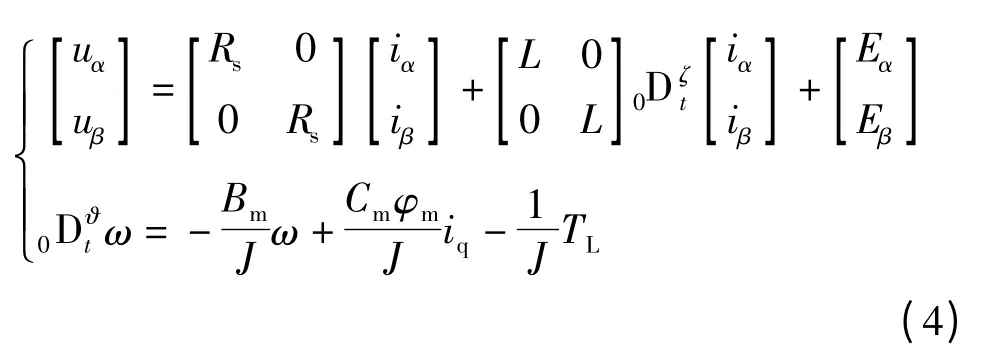
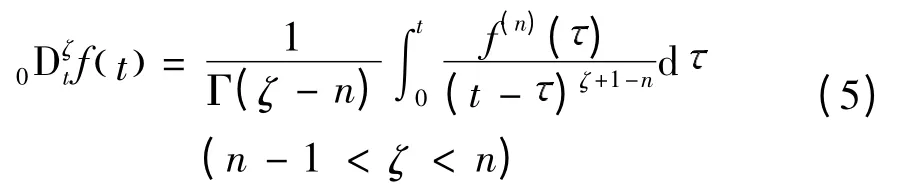
式中，Γ(·) 为Gamma 函数，其表达式为Γ(z) =

2 分数阶滑模观测器(FO-SMO)设计

图1给出了建立在分数阶永磁同步电机数学模型基础上的分数阶滑模观测器系统框图.系统由两部分组成.其中，位于虚线框外面的是真实的永磁同步电机系统模型;而位于虚线框里面的则包含永磁同步电机动态模型及分数阶滑模观测器两个模块.

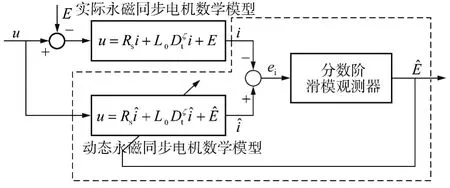
图1 基于分数阶永磁同步电机数学模型的分数阶滑模观测器系统框图Fig.1 Block diagram of fractional order sliding mode observer system based on fractional order mathematical model of PMSM

2.1 观测器设计

依据永磁同步电机在两相静止α，β 坐标系下的分数阶定子电压方程，构造滑模观测器为

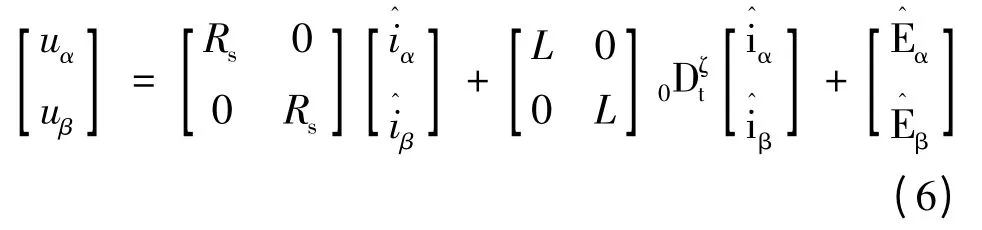
将永磁同步电机在两相静止定义α，β 坐标系下的分数阶定子电压方程(4)与相应的动态方程(6)相减，并定义观测误差，可得到定子电流误差系统方程为

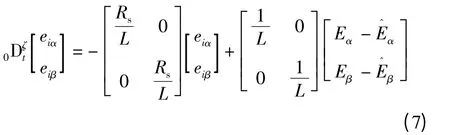
针对滑模观测器系统，设计切换函数:

式中，λ为滑模面增益，r 为分数阶微积分的阶次.

2.2 可达性证明

为证明系统能由任意初始状态在有限时间内到达滑模面，构造Lyapunov 函数V:

考虑到式(7)中的微分项阶次为分数阶，若直接对Lyapunov 函数一阶求导，则加大了对系统稳定性进行论证的复杂度［11-12］.因此，对Lyapunov 函数进行分数阶求导，则有:

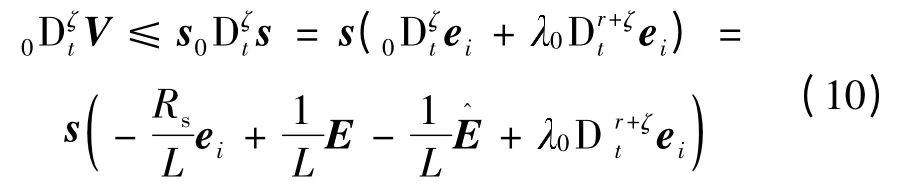
其中，

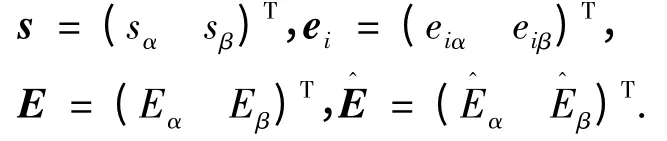
因此，令

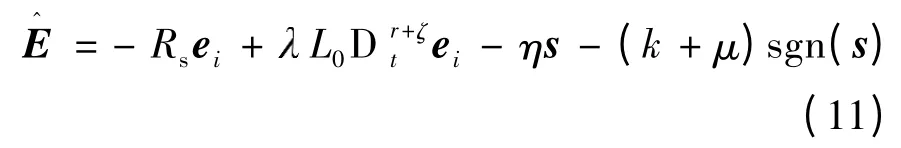
并代入式(10)中，可得:

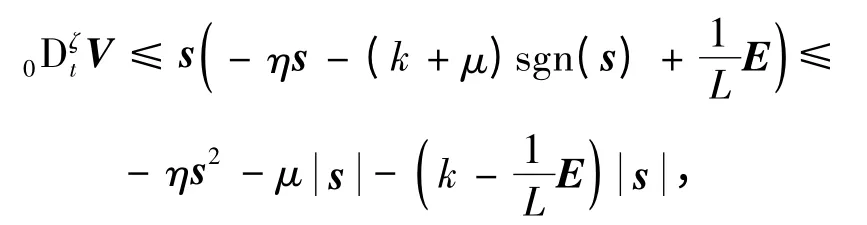
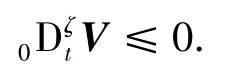
根据Lyapunov 稳定性理论，系统能由任意初始状态在有限时间内收敛到切换流行面.

2.3 滑模观测器参数整定

滑模观测器中的系统运行轨迹分为趋近模态与滑动模态两个过程［13］.分析式(11)可知，当s = 0时，即说明系统当前的运行轨迹到达滑模面，并开始进行滑模运动，此时可改写式(11)为

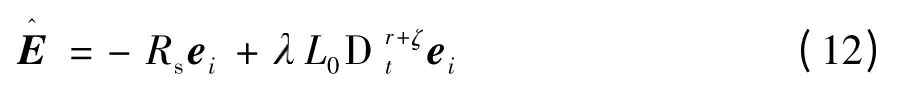
分析图1中虚线框内的系统结构，并结合考虑滑模运动状态下的控制率方程(12)及永磁同步电机动态模型方程(6)，可画出相应的系统等效结构图，如图2所示.

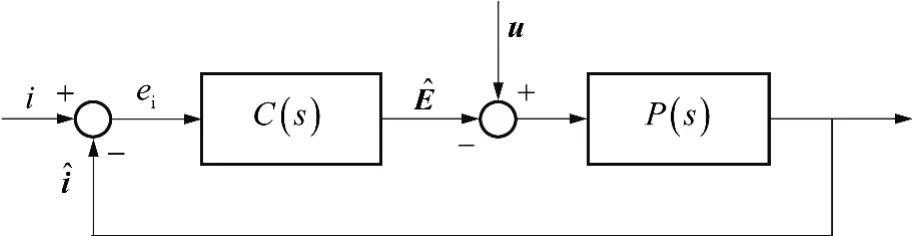
图2 系统等效结构图Fig.2 Equivalent structure diagram of system

从图2中可以看出，将永磁同步电机动态模型

(6)转化为传递函数形式，可得:

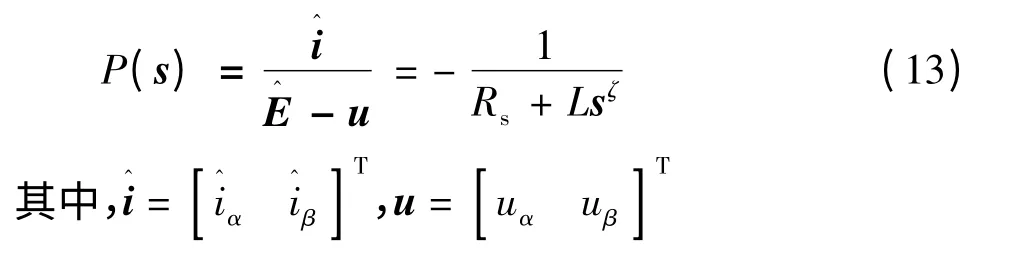
在滑模运动状态下，控制率(12)也可转化为传递函数，即

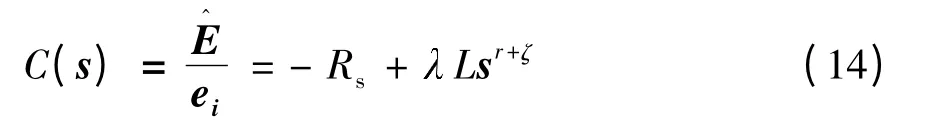
根据式(13)及式(14)，可得出系统开环传递函数G(s)的形式为

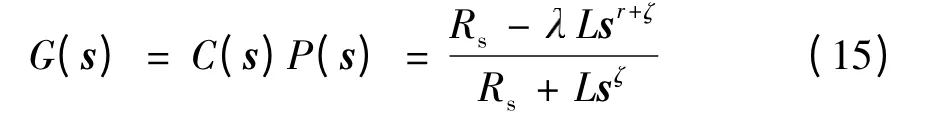
下面是3 条设计准则［14］:

(1)相角裕度准则

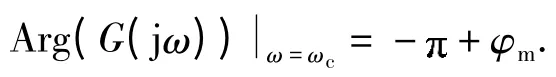
(2)穿越频率准则

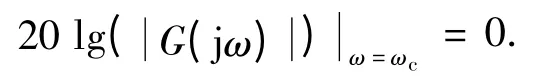
(3)增益变化鲁棒性准则

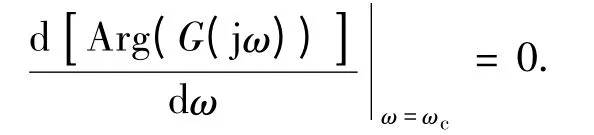
其中，ωc为幅频特性曲线的截止频率，φm为相角裕度.

联立由3 条设计准则构造得出的方程，可得:

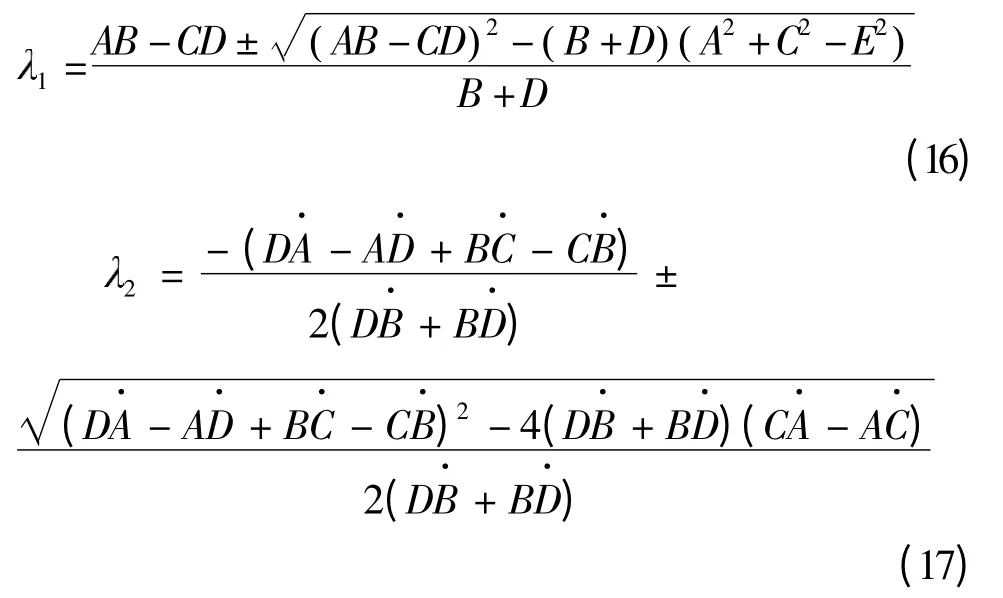
其中:

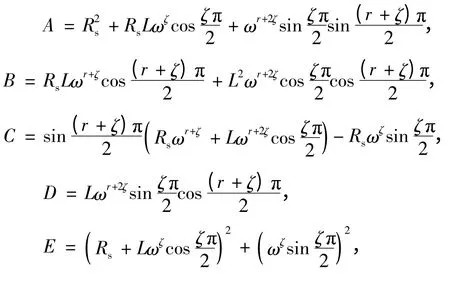
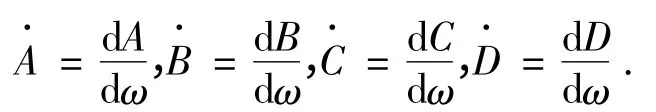
根据式(16)及式(17)，可绘出 1 和 2 关于r 变化的两条曲线，如图3所示.

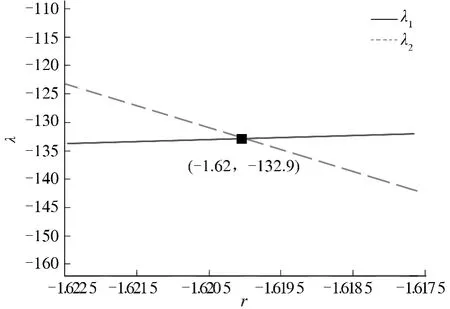
图3 随r 变化的曲线Fig.3 Curves of changing with r

求解图3中两条曲线的交点，可得到分数阶滑模观测器方程(8)中的结构参数分别为 = -132.9及r = -1.62 .所设计出的基于分数阶滑模观测器与分数阶模型的永磁同步电机无位置传感器控制系统的波特图如图4所示.

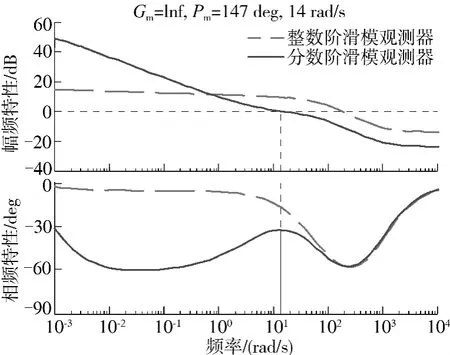
图4 整数阶、分数阶滑模观测器作用下的系统波特图Fig.4 System Bode diagrams with IO-SMO and FO-SMO

从图4中可以看出，系统截止频率和相角裕度均满足设计要求;且在截止频率处，相频特性曲线的斜率为零，满足增益变化鲁棒性准则的要求.

3 启动过程分析

文中提出的永磁同步电机无位置传感器控制系统为矢量控制系统.当电机转速位于零速或附近的低速范围内时，无法避免控制死区及观测死区的问题，此时矢量控制系统内的转速环为开环状态.因此，为保证电机能够平滑启动或停机，须保证系统产生的定子圆形旋转磁场的幅值与相角能稳定地增大或减小.图5给出了启动过程中电压空间矢量的变化规律，图中α 轴与β 轴分别代表电压空间矢量在静止两相αβ 坐标系下的分量;相互嵌套的虚线圆为电压空间矢量在幅值恒定时旋转一周所产生的状态轨迹;U1-U6为按逆时针旋转顺序增大的6 个电压空间矢量，随着矢量幅值的增大，电机转速也将相应地增大，从而实现电机的平滑启动.

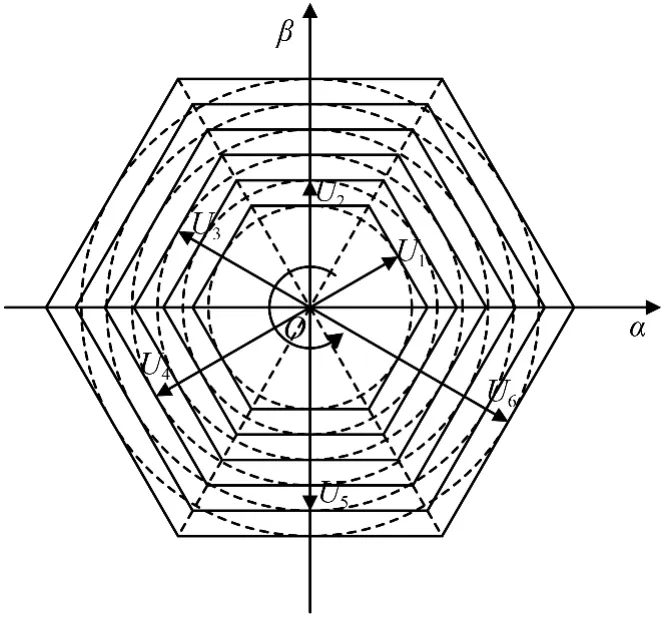
图5 定子电压空间矢量变化规律Fig.5 Changing patterns of stator voltage space vector

4 仿真结果与讨论

以Matlab 软件为仿真平台.其中电机参数:Rs=1.32 Ω，L = 0.0261H，J = 25.1 ×10-3kg·m2，Bm=0.8 ×10-3N·m·s，参考文献［15］，设定分数阶模型的阶次分别为ζ = 0.9219，ϑ = 0.9534.

将分数阶算子sζ近似为有限维的离散传递函数，设置采样周期为0.000125 s，则有:

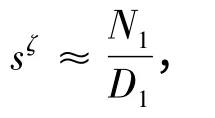
其中:

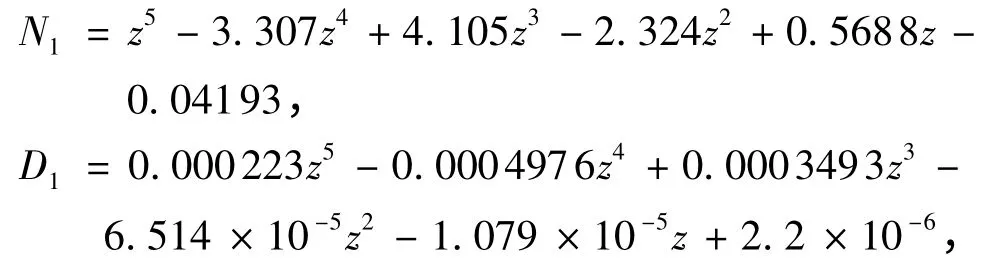
从而，即可得到分数阶滑模观测器Rs- Lsr+ζ的近似表达形式为，其中:

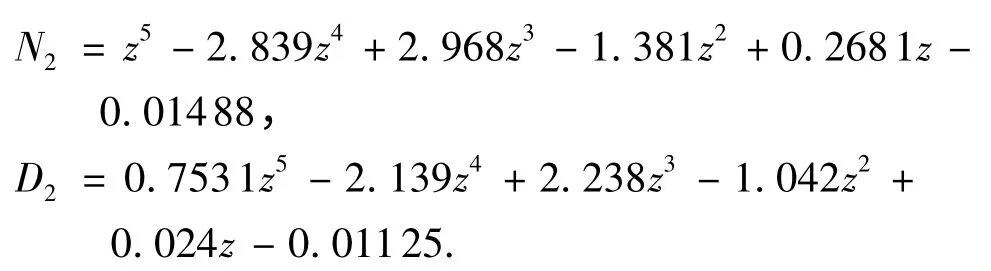
在Matlab/Simulink 环境下，按照实际的永磁同步电机无位置传感器控制系统进行建模与仿真，设置给定输入为斜坡信号与正弦信号的分段叠加以区分不同的控制策略［16］，响应曲线如图6-9 所示.

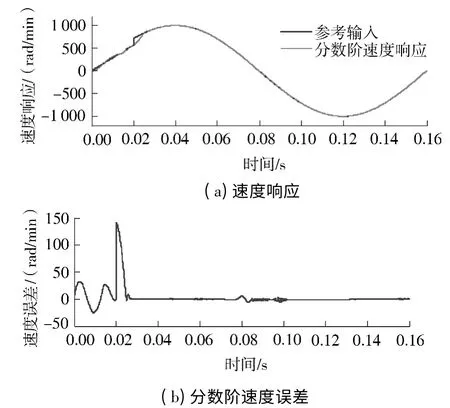
图6 分数阶滑模观测器作用下的正弦响应曲线Fig.6 Sinusoidal response curves under the influence of FOSMO

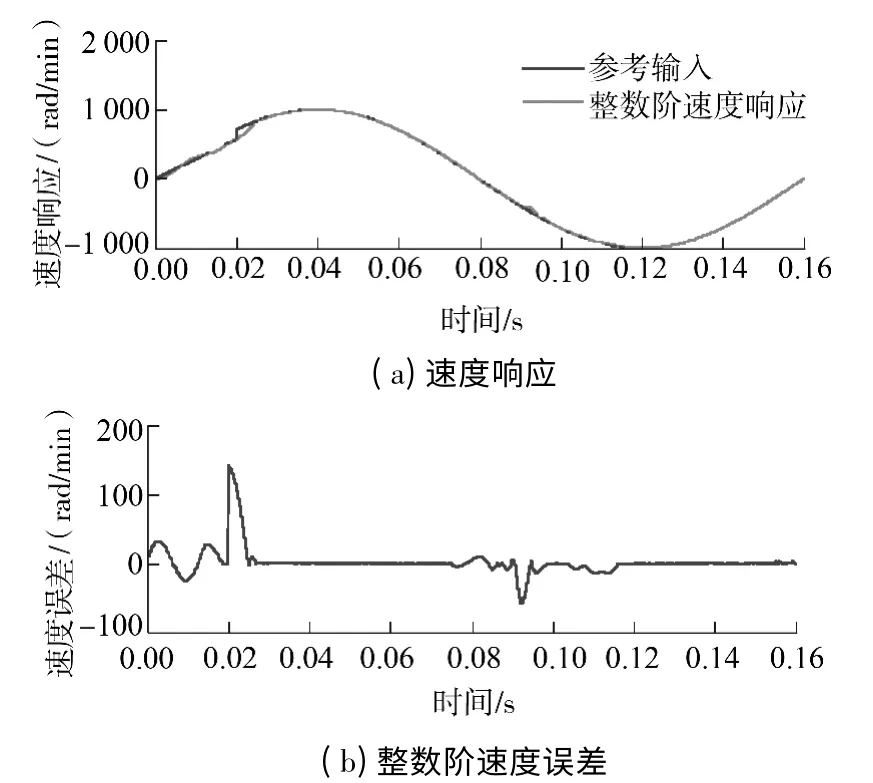
图7 整数阶滑模观测器作用下的正弦响应曲线Fig.7 Sinusoidal response curves under the influence of IO-SMO

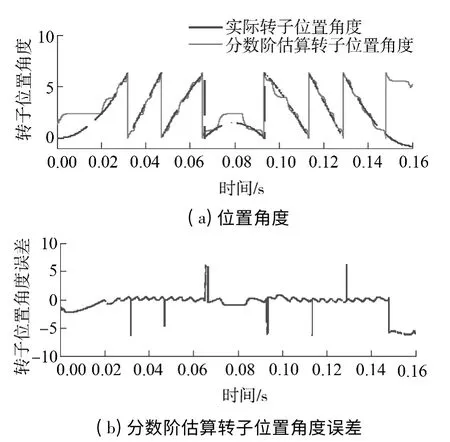
图8 分数阶滑模观测器作用下的转子位置对比曲线Fig.8 Comparison of rotor position curves under the influence of FO-SMO

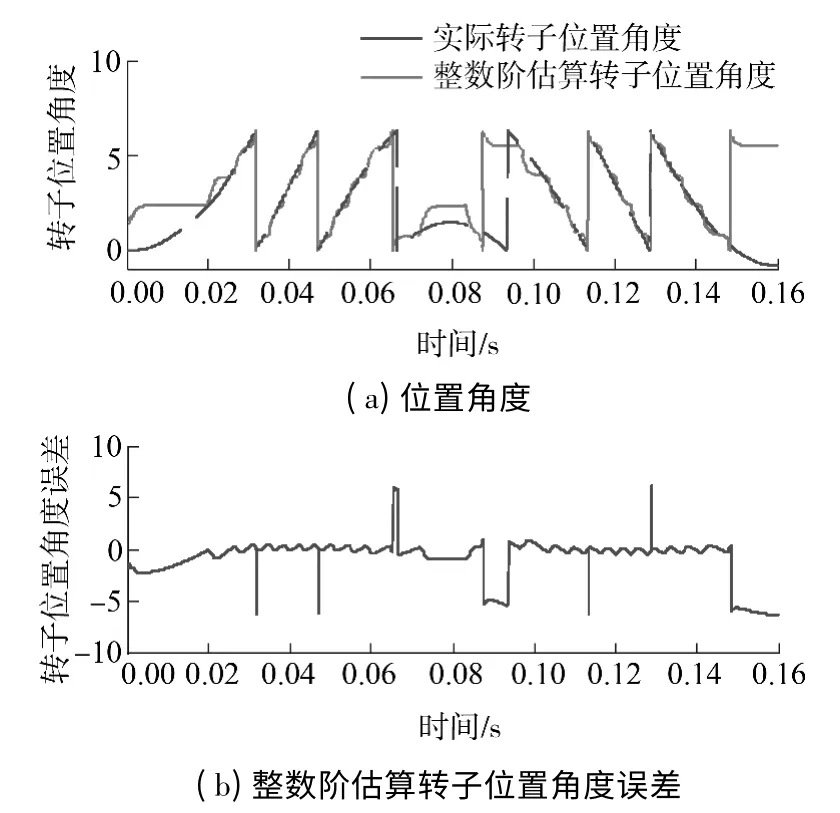
图9 整数阶滑模观测器作用下的转子位置对比曲线Fig.9 Comparison of rotor position curves under the influence of IO-SMO

根据图6-9 给出的正弦响应特性曲线与转子位置对比曲线，采用时间乘以误差绝对值积分ITAE性能指标对其进行衡量.其数学表达式为

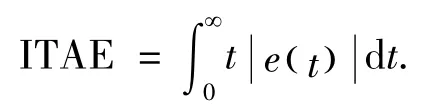
其中，t 为时间，e(t) 为误差.依据ITAE 性能指标，可得到整数阶滑模观测器与分数阶滑模观测器分别作用于永磁同步电机无位置传感器控制系统上的系统控制效果，如表1所示.

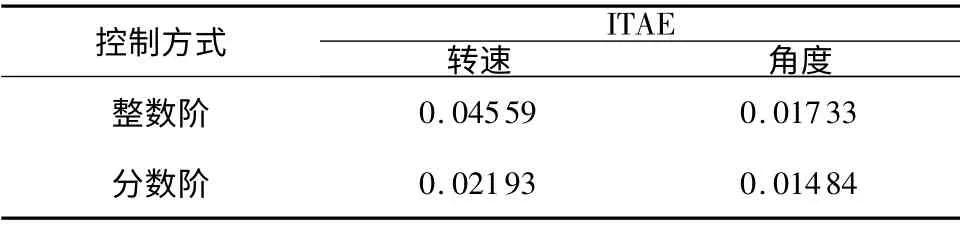
表1 两种控制方式下的ITAE 值对比Table1 Comparison of ITAE under two kinds of control strategy

从表1可以看出，分数阶滑模观测器作用下的永磁同步电机无位置传感器控制系统比整数阶滑模观测器能够获得更好的综合控制性能.

5 实验

将文中提出的控制策略在永磁同步电机伺服系统进行实验验证，实验平台如图10所示.主控板的核心是DSP 处理器，其具体型号为TMS320F2812.PC 机主要通过采集伺服电机反馈的数据进行分析比较，编码器则用于将实际转子位置角度与预测转子预测角度进行对比.实验结果如图11-14 所示.

图11、12 给出了分数阶与整数阶滑模观测器分别作用下永磁同步电机无位置传感器控制系统的正弦响应曲线及相应的误差曲线，其中，纵坐标以标幺值的方式进行显示.对比两张图可以看出，相比整数阶滑模观测器，分数阶滑模观测器作用下的系统正弦响应在电机他控启动及控制方式切换后具有较小的误差波动，能更好地实现两种控制方式间的平滑切换.

图10 实验平台Fig.10 Experiment platform

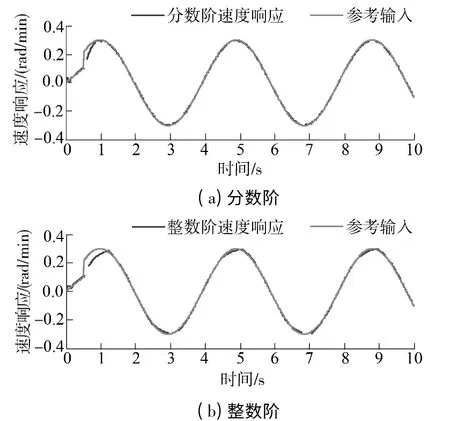
图11 分数阶与整数阶滑模观测器作用下的系统正弦响应曲线Fig.11 System sinusoidal responses curves under the influence of FO-SMO and IO-SMO

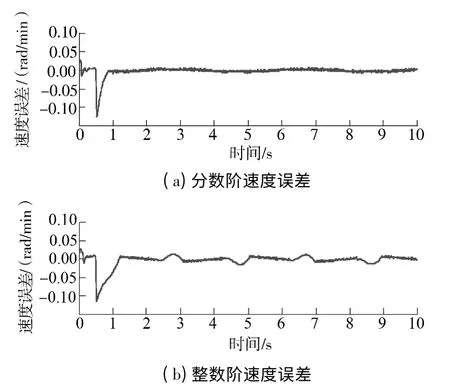
图12 分数阶与整数阶滑模观测器作用下的系统正弦响应误差曲线Fig.12 Error curves of system sinusoidal responses under the influence of FO-SMO and IO-SMO

图13、14 给出了分数阶与整数阶滑模观测器分别作用下永磁同步电机无位置传感器控制系统的估算转子位置及实测转子位置对比及误差曲线，其中，纵坐标以标幺值的方式进行显示.对比两张图可以看出，分数阶滑模观测器作用下的估算转子位置与实测转子对比曲线相比整数阶滑模观测器误差较小.

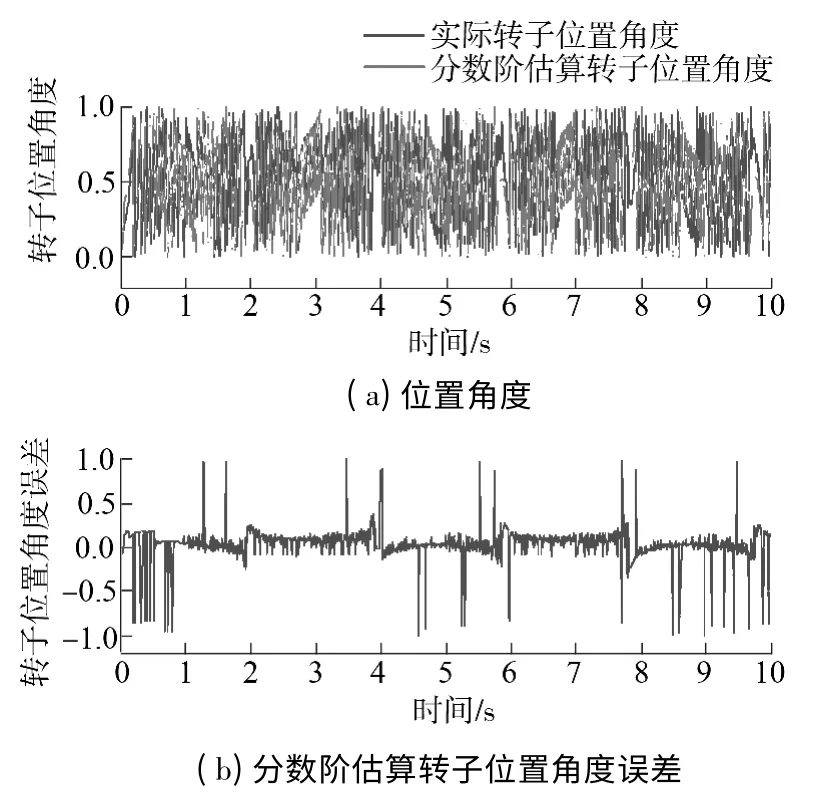
图13 分数阶滑模观测器作用下的转子位置对比曲线Fig.13 Comparison of rotor position curves under the influence of FO-SMO

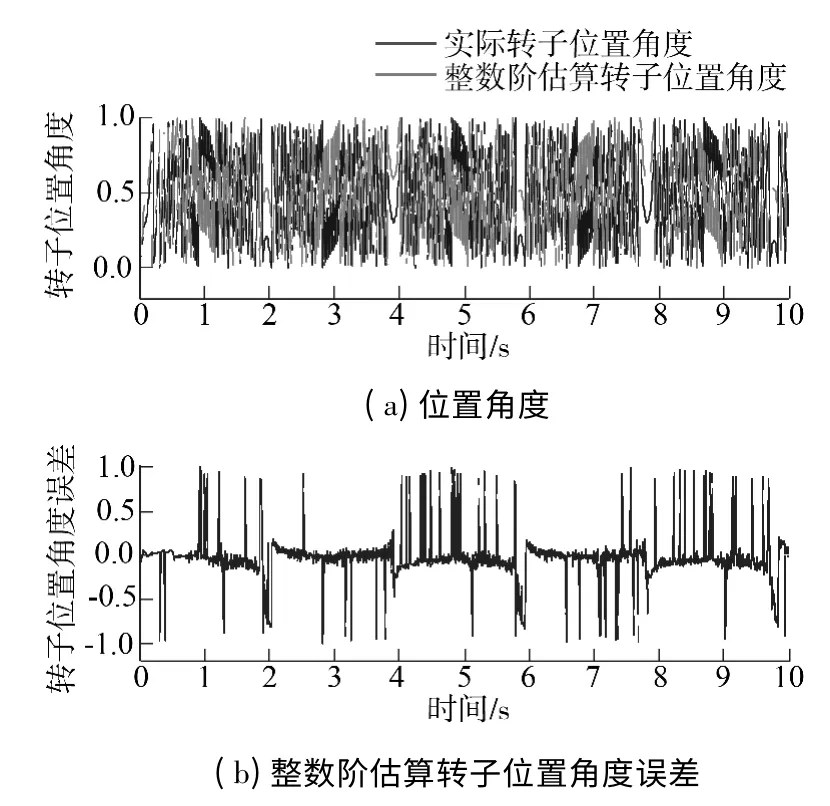
图14 整数阶滑模观测器作用下的转子位置对比曲线Fig.14 Comparison of rotor position curves under the influence of IO-SMO

6 结语

针对永磁同步电机无位置传感器控制系统中存在的无法零速启动的问题，设计了他控启动以及由他控方式向自控方式切换的分段控制策略.为消减控制方式切换过程中所产生的转速抖振，引入了分数阶模型及分数阶滑模观测器理论以提高系统的控制与观测精度，并给出了系统稳定性分析.仿真和实验证明，文中提出的控制策略不但实现了电机的平滑启动，而且明显削弱了控制方式切换过程中所带来的转速抖振.

［1］Chen J L，Tseng S K，Liu T H.Implementation of highperformance sensorless interior permanent-magnet synchronous motor control systems using a high-frequency injection technique［J］.IET Electric Power Applications，2012，6(8):533-544.

［2］Frederik M De Belie，Peter Sergeant，Jan A Melkebeek.A sensorless PMSM drive using modified high-frequency test pulse sequences for the purpose of a discrete-time current controller with fixed sampling frequency ［J］.Mathematics and Computers in Simulation，2010，81(2):367-381.

［3］Aydogmus O，Sünter S.Implementation of EKF based sensorless drive system using vector controlled PMSM fed by a matrix converter［J］.International Journal of Electrical Power ＆ Energy Systems，2012，43(1):736-743.

［4］袁雷，沈建清，肖飞，等.插入式永磁低速同步电机非奇异终端滑模观测器设计［J］.物理学报，2013，62(3):030501/1-9.Yuan Lei，Shen Jian-qing，Xiao Fei，et al.Nonsingular terminal sliding-mode observer design for interior permanent magnet synchronous motor drive at very low-speed［J］.Acta Physica Sinica，2013，62(3):030501/1-9.

［5］尚喆，赵荣祥，窦汝振.基于自适应滑模观测器的永磁同步电机无位置传感器控制研究［J］.中国电机工程学报，2007，27(3):23-27.Shang Zhe，Zhao Rong-xiang，Dou Ru-zheng.Research on sensorless control method of PMSM based on an adaptive Sliding Mode Observer ［J］.Proceedings of the CSEE，2007，27(3):23-27.

［6］周永勤，王旭东，张玉光，等.开关磁阻电机模糊滑模观测器间接位置检测［J］.电机与控制学报，2013，17(6):57-63.Zhou Yong-qin，Wang Xu-dong，Zhang Yu-guang，et al.Sensorless detection technique on fuzzy sliding mode observer for SRM ［J］.Electric Machines and Control，2013，17(6):57-63.

［7］辛凯，詹琼华.基于滑模观测器的开关磁阻电动机间接位置检测技术研究［J］.微电机，2007，40(9):9-13.Xin Kai，Zhan Qiong-hua.Sensorless control of switched reluctance motor driver based on sliding mode rotor position observer［J］.Micromotors Servo Technique，2007，40(9):9-13.

［8］张旭龙，谭国俊.在线建模的开关磁阻电机四象限运行无位置传感器控制［J］.电工技术学报，2012，27(7):26-32.Zhang Xu-long，Tan Guo-jun.Four-quadrant position sensorless control of switched reluctance motors based on online modeling［J］.Transactions of China Electrotechnical Society，2012，27(7):26-32.

［9］Lin F J，Shen P H.Robust fuzzy neural network slidingmode control for two-axis motion control system ［J］.IEEE Transactions on Industrial Electronics，2006，53(3):1209-1225.

［10］Yu Wei，Pi You-guo.Fractional order modeling and simulation experiment of permanent magnet synchronous motor［J］.MESA，2012(7):114-118.

［11］Norelys Aguila Camacho，Manuel A Duarte Mermoud，Javier A Gallegos.Lyapunov functions for fractional order systems ［J］.Commun Nonlinear Sci Numer Simulat，2014，19(9):2951-2957.

［12］Trigeassou J C，Maamri N，Sabatier J，et al.A Lyapunov approach to the stability of fractional differential equations［J］.Signal Processing，2011，91(3):437-445.

［13］高为炳.变结构控制的理论及设计方法［M］.北京:科学出版社，1996.

［14］Luo Ying，Chen Yang-quan.Fractional order ［proportional derivative］controller for a class of fractional order systems［J］.Automatica，2009，45(10):2446-2450.

［15］余伟，皮佑国.永磁同步电机分数阶建模与实验分析［J］.华南理工大学学报:自然科学版，2013，41(8):55-61.Yu Wei，Pi You-guo.Fractional order modeling and experimental analysis of permanent magnet synchronous motor［J］.Journal of South China University of Technology:Nature Science Edition，2013，41(8):55-61.

［16］Chi W C，Cheng M Y.Implementation of a sliding-modebased position sensorless drive for high-speed micro permanent-magnet synchronous motors ［J］.ISA Transactions，2014，53(2):444-453.