基于设计结构矩阵的船舶MDO建模*

刘强 冯佰威 刘祖源

(武汉理工大学 交通学院，湖北 武汉430063)

多学科设计优化(MDO)建模是确定设计需求所包含的各个方面的具体表达，并且将这种表达转化为优化算法所需的模型［1］.然而，目前并没有成熟的针对于一般产品的MDO 建模技术.对于船舶多学科设计优化研究，建模技术也不是研究的重点［2-8］，因此所采用的建模技术往往仍是按照传统的学科划分构建本学科的数学模型，然后以这些模型为基础，构造出MDO 的数学模型.这种建模方法对各学科的建模，均采用传统的优化数学模型，因而往往有着成熟的经验公式和数值计算方法作为支撑.但是这种方法在建模过程中并没有考虑到各学科之间的耦合作用，导致最后建立的MDO 模型存在大量耦合，造成优化效率降低.

由于降低优化过程中的信息交互量能间接降低设计优化的计算复杂性［9］，因而文中提出一种基于设计结构矩阵聚类运算的建模方法.通过该方法对传统的船舶MDO 概念模型进行重组，降低该模型的耦合程度，建立新的船舶MDO 概念模型.

1 聚类算法

1.1 算法概述

设计结构矩阵(DSM)是一种主要应用于工程设计领域的、支持产品设计开发及过程建模的强有力工具.聚类是设计结构矩阵的几种运算之一，其作用是将DSM 中联系紧密的元素归为一类［10］.对于船舶MDO 而言，其所包含的各个学科可以视为工程设计中不同的开发团队，因而船舶MDO 可以视为一种特殊的基于团队的DSM.DSM 的聚类能够将复杂产品分解成为规模较小的、易于开发的、有独立功能的、可独立(或相对独立)进行开发的子系统.将此运算应用于船舶MDO 模型，就可以重组船舶传统的学科，形成新的学科划分.新的学科划分相对于传统的学科划分而言，每个学科内部所包含元素之间的联系强度很高，而学科与学科之间的联系强度却很低.在此基础上，构建出的MDO 模型将有效地减少学科之间的耦合，可以节省MDO 优化的时间并为并行计算创造条件.

聚类运算由于评价聚类方案标准和所采用优化方法的不同而存在多种算法.文中选择基于联系信息流量的聚类算法［11］并加以改进，将其用于对船舶MDO 概念模型的重组.该算法采用联系信息流量作为评价标准，采用遗传算法作为优化方法得到最优的聚类方案.该方法无需限定聚类数目和大小，不需要太多的人工干预，无论对于布尔型还是数字型DSM 均适用，另外对于大规模的DSM，算法也具有很好的适应性.

1.2 聚类的评估标准和假设

为了从众多的聚类方案中选择最优的方案，需要建立评价标准和方法对这些方案进行评估.

根据文献［11］，给出如下定义.

定义1联系信息流量

DSM 模型中行列元素之间的联系所涉及的相关的交互管理信息的总量，称为联系信息流量.

定义2聚类规模

在DSM 中，一个聚类所包含的行列元素的数目被称为聚类规模.该DSM 所包含的行列元素的数目为该DSM 模型的规模.

定义3联系权重

在DSM 中，矩阵单元中的数值称之为对应行列元素的联系权重.第i 行第j 列矩阵单元的联系权重记为di，j.

以文献［11］为基础，改进后的算法假设如下.

1)行列元素之间联系信息流量与联系的权重成某种函数关系;

2)较小聚类中的行列元素之间的联系比较大聚类中的联系更加容易管理;

3)聚类之间联系的管理难度随着聚类所含行列元素的增长而增大;

4)同一个聚类内部的行列元素之间联系的管理难度比属于不同聚类的元素之间联系的管理难度低.

文献［11］中假定行列元素之间的联系信息流量与联系的权重为线性函数.然而根据系统工程理论的相关知识［12］，对于由各子系统组合而成的大系统，即使其每个子系统都是线性的，大系统本身不一定是线性.也就是说，随着联系权重的增加，该单元的联系信息流量并不一定成正比增加.所以仅仅假定它们是线性关系，是不够准确的.文中假定行列元素之间联系信息流量与联系的权重成某种函数关系，即Di，j= f(di，j).

1.3 算法流程

元素可以分为3 类:

第1 类为独立元素，这类元素比较独立地存在于整个DSM 模型之中，不属于任何聚类，并且很少受到其他元素的影响，也很少影响到其他元素.在MDO 中，这类元素可以是比较独立的子目标，它的优化不需要其他子目标的较多输入，同时也不会给予其他子目标较多的输出.

第2 类为BUS 类元素.这类元素与其他大部分行列元素都有联系.所有BUS 元素构成一个BUS 聚类.在MDO 中，这类元素可以是系统层的目标或者系统设计变量，它的计算需要许多子目标的输入，而它的改变同时又有可能给多个子目标带来影响.

第3 类为普通聚类元素.这类元素存在于普通聚类当中，普通聚类可以有多个.在MDO 中，这些元素可以是子系统中所包含的子目标或学科内部的局部设计变量.

聚类算法的寻优采用遗传算法，一般步骤如下.

1)独立元素的识别与分离;

2)根据独立元素分离后的DSM，生成多种聚类方案.每一个聚类方案对应一条染色体，从而构成初始种群.执行选择、交叉和变异算子，反复迭代直到满足收敛条件为止.将最终结果输出并解码，得到DSM 的最优聚类方案;将之前删掉的独立元素添加到DSM 的最前方，构成最终的聚类方案.

聚类算法流程图如图1所示.

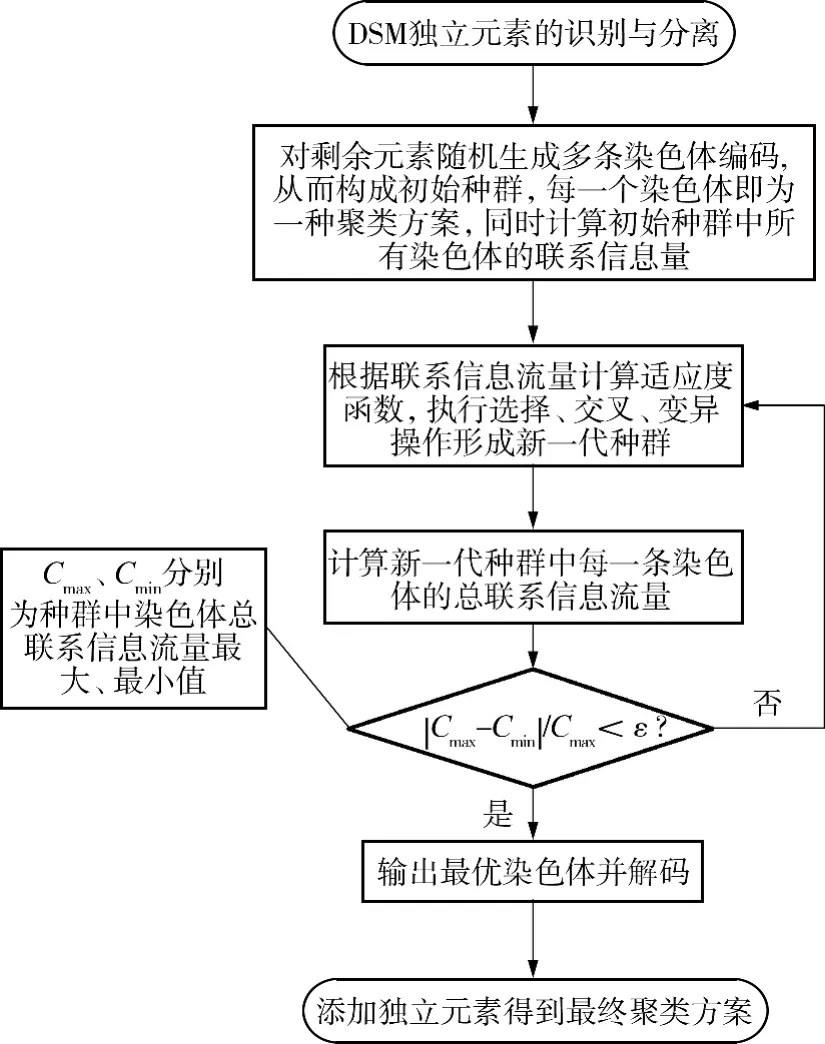
图1 聚类算法流程图Fig.1 Flow chart of clustering algorithm

首先介绍文献［11］中的编码方式.

记DSM 经过独立元素分离后的规模为n，对该模型的行列元素按顺序依次编为E1，E2，…，En，其中任意一行列元素Ei对任意另外一行列元素Ej的单元格为联系权重di，j(1≤i≤n，1≤j≤n，i≠j)，当i=j时，该单元格为对角线上的单元格，没有意义，此时di，j=0.假定该模型的最大聚类数为m，则构建一个m ×n 的二维编码矩阵.编码矩阵的每一行对应一个聚类，依次记为CLi(i 从1 到m)，其中最后一行对应BUS 聚类;编码矩阵的每一列对应一个行列元素，行列元素的顺序与聚类前模型中的行列元素顺序保持一致(E1，E2，…，En);编码矩阵的每个单元格表示它所对应的行列元素是否在它所对应的聚类中，如果在，值为1，如果不在，值为0.

采用这种编码方式得到的染色体，记为ch，是一个m × n 的矩阵，共包含n 个元素.对于每一个元素而言，都需要m 个单元记录其所属聚类的信息，而其中仅有1 个内容为1 的单元信息是有用的.采用这种编码方式不但浪费信息存储的空间，而且对于其后的交叉和变异操作来说也不是必须的.因此，对这种编码方式新增一步映射，对于每一个元素而言，无须记录其在所有聚类中的信息，而只需要记录其所在聚类的编号.假设有一个包含6 个元素的DSM，共有4 个聚类.其元素E1、E2、E4属于第1 个聚类，E3、E5属于第2 个聚类，第3 个聚类为空，E6属于BUS 聚类.则按照原方法的编码如表1所示.改进后的编码如表2所示.其中编号4 为BUS 聚类.

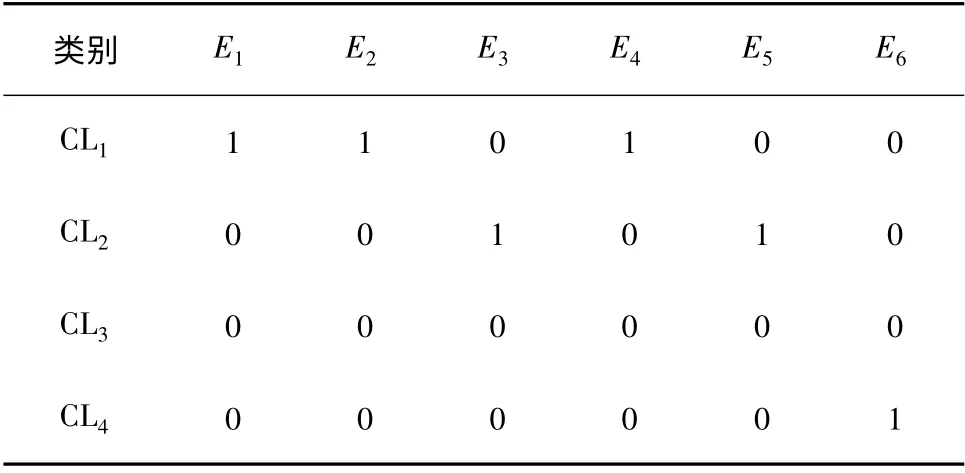
表1 原编码Table1 Original coding

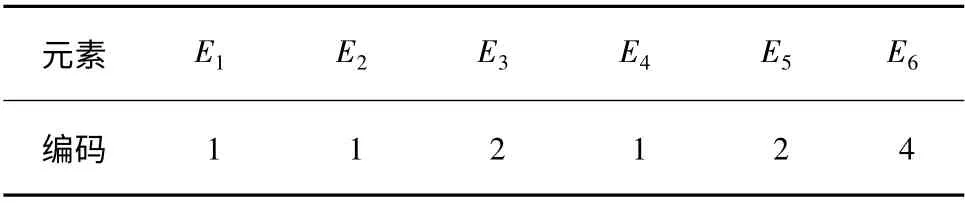
表2 改进后编码Table2 Improved coding

有了聚类方案的染色体编码方式，就可以进行种群的初始化.对于一定规模的DSM，可以假定一定数目的聚类，其中最后一个聚类为BUS 聚类.文中利用随机数发生器，对每一个元素随机生成其所在聚类的编号，直到生成一条染色体.重复该操作，直到生成有足够多条染色体的初始种群.关于适应度函数计算和选择、交叉和变异算子，可以参见文献［11］.

2 算例验证和改进

2.1 线性函数与算例验证

文献［11］中对于Di，j= f(di，j)采用线性函数，即:Di，j=di，j.为验证算法的聚类效果，对产品设计开发领域的一个摩托车发动机DSM 进行了聚类.DSM 如表3所示.

表3中对角线下方的矩阵单元格标识表示方向为正向的关系，对角线上方的单元格标识表示方向为反向的关系，这些单元格中的数字为对应的行列元素之间的联系权重，空白矩阵单元格表示对应的行列元素之间没有联系，对角线单元没有意义，用黑块标识.

遗传算法的运行参数主要有种群大小、交叉概率、变异概率等.种群大小较小，有利于提高算法的运算速度，但是也降低了种群的多样性.种群大小过大，算法的运行效率会大大降低.交叉概率太大会破坏群体中的优良模式，过小会使产生新个体的速度变慢.变异概率过小会降低变异算子抑制早熟和产生新个体的能力，过大又会破坏染色体中较好的模式.文中选取多个遗传算法参数组合对该例子进行试算，在交叉概率为0.8、变异概率为0.1、种群大小为5 000 时，得到最优方案(9 505.4).故在下文的计算中，均取交叉概率为0.8，变异概率为0.1，种群大小为5 000.由于所采用的种群大小远高于文献［11］，文中所得到的聚类方案与其并非完全一致.实际上，文中所得的方案要略优于文献［11］，比较二者实际的聚类方案，可以发现二者基本上是一致的，只是5、21、29 这3 个元素的分类不同.二者的聚类方案对比如表4所示.

2.2 指数函数改进和评价标准

根据1.2 节对基本假设的改进，采用指数函数来改善聚类结果.对摩托车发动机DSM，采用Di，j= exp(β(di，j-1))来计算联系信息流量，其中β 为松弛因子，用来控制所采用指数函数的区间长度.对该DSM 而言，β 分别取1/9、1/6、1 和4/3 时，所对应的指数区间分别为［0，1］、［0，1.5］、［0，3］和［0，4］.由于指数函数增长速度远大于线性函数，用指数函数取代线性函数来表征较大权重对总联系信息流量的影响相对而言更为合理.

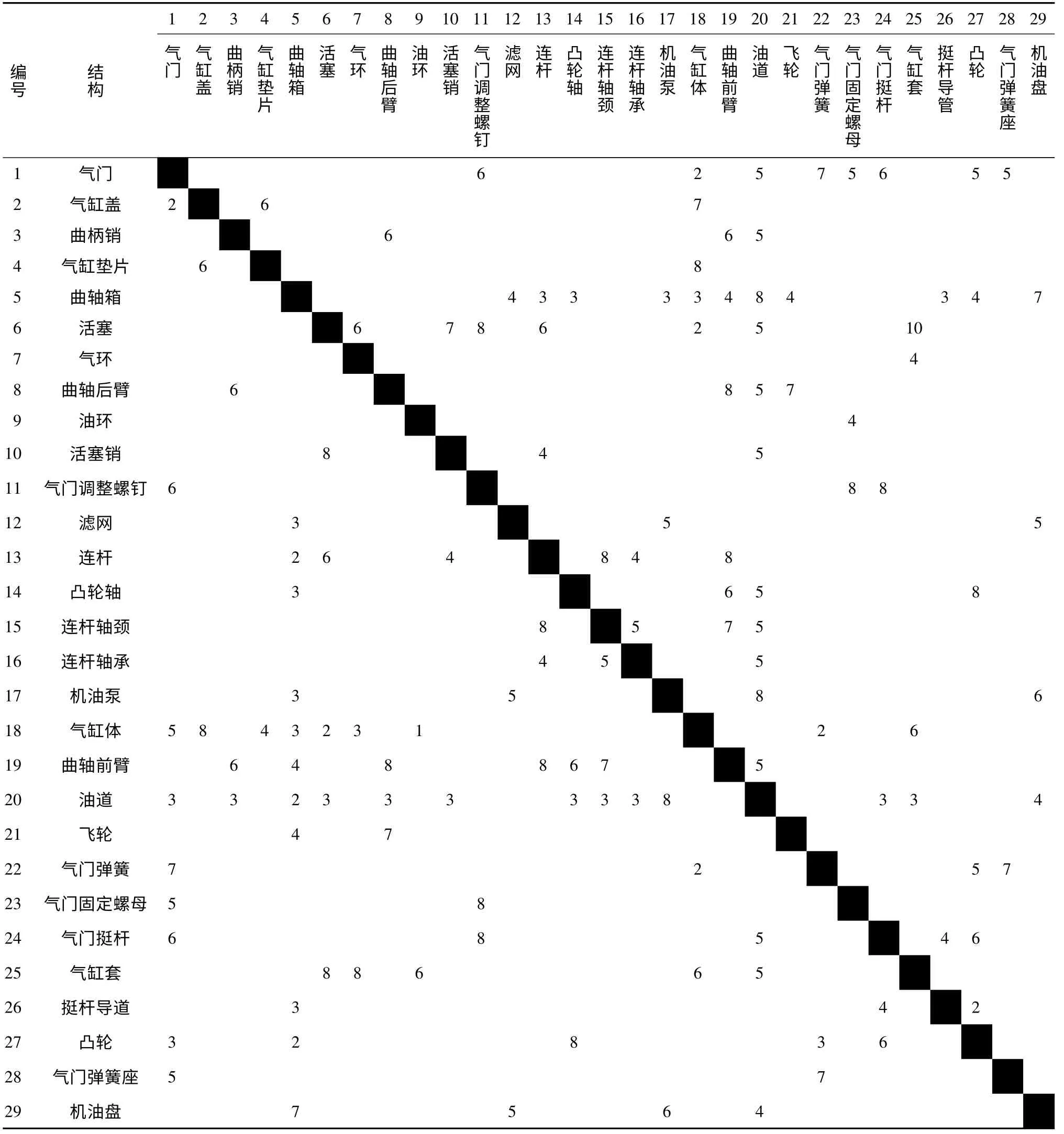
表3 摩托车发动机DSMTable3 A DSM of motor engine

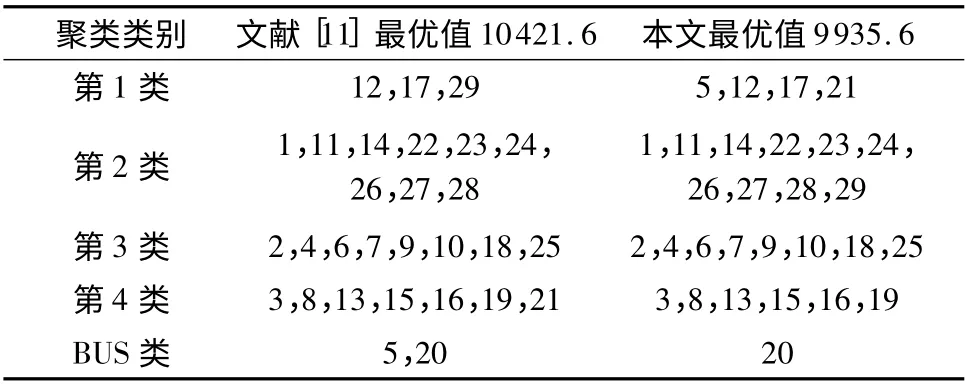
表4 二者聚类方案对比Table4 Comparison of two solutions

线性函数假定和指数函数假定的计算方式不同，所以通过比较联系信息流量来评价两种方法的优劣是不可行的.故针对聚类方案提出如下两个指标作为判断聚类结果的依据.

1)联系权重在聚类内部中的百分比

联系权重在聚类内部中的百分比是指经过聚类重组之后，在聚类内部的各种权重的矩阵单元占其总数的百分比.该指标越大，表明存在聚类内部的权重越多，元素之间的联系就越多地集中于聚类内部.

2)BUS 聚类规模

该指标是指BUS 聚类所含元素的个数.BUS 聚类的规模越大，与其他普通聚类的联系就越多.所以BUS 聚类的规模越小越好.

以上两项指标均很重要，高的百分比不一定意味着好的聚类方案.例如，对于只有一个BUS 聚类的聚类方案.各项权重所占百分比均为100%，但是BUS 聚类规模也最大，实际上没有起到聚类的作用.

2.3 指数函数与算例验证

仍以摩托车发动机DSM 为例，表5给出了线性方法下的计算结果和不同β 下聚类结果的权重百分比及BUS 聚类规模.

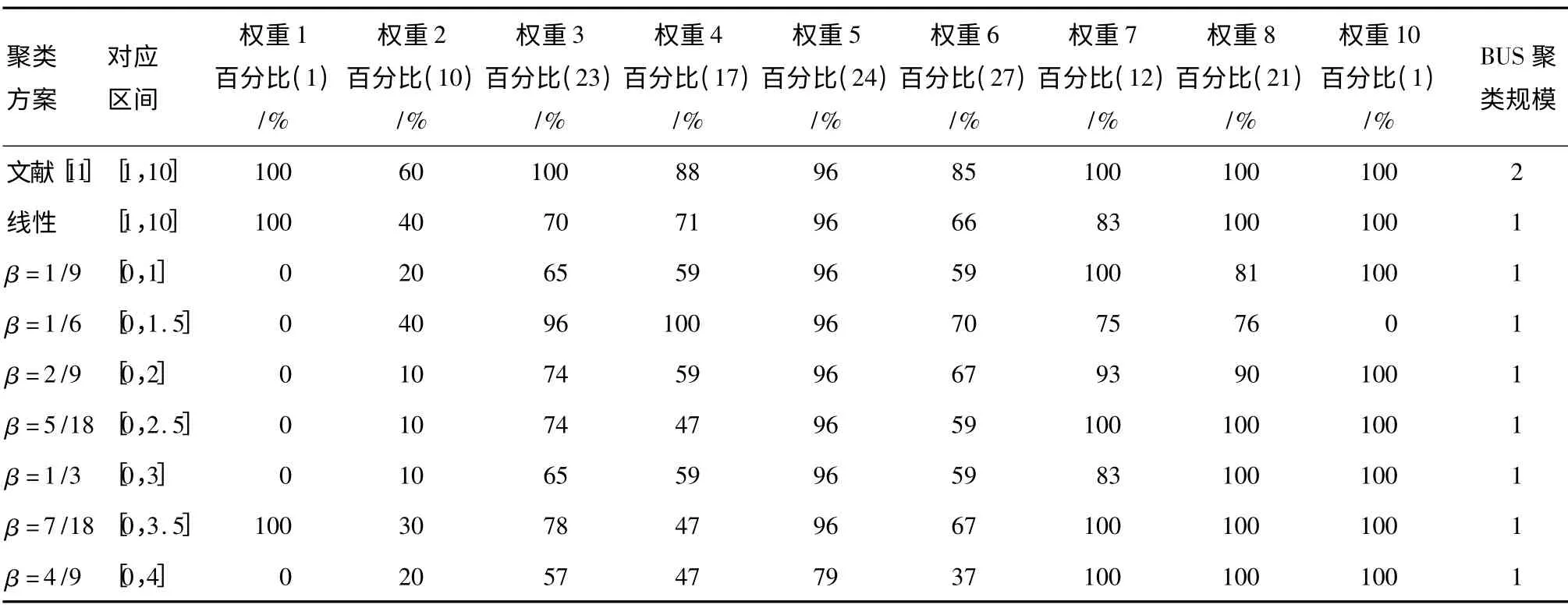
表5 聚类结果比较1)Table5 Comparison of optimal solutions

当β=7/18 时，获得了最优的聚类结果.将该聚类方案与线性假定下的两个方案相比较.与文献［11］相比其权重百分比处于劣势，但是减少了BUS 聚类规模;与文中线性函数下聚类结果相比，在保持了BUS 聚类规模的同时，虽然在较小权重上损失了百分比(权重2，4)，但提高了较大权重在聚类内部的百分比(权重7).其具体聚类方案如表6所示.

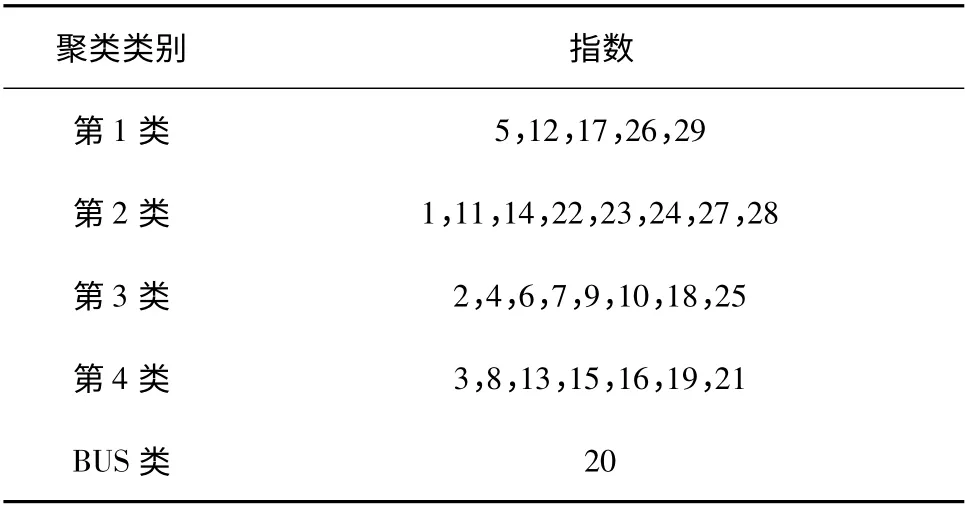
表6 指数假定下的最优聚类方案Table6 Optimal solution under hypothesis of exponential function

与表4对比可以发现，该聚类方案与文中线性聚类方案基本一致，只是21、26 号元素所属聚类发生了变化.

2.4 算例验证和改进总结

首先比较线性函数假定下的两种聚类结果(如表5所示)，可以看出，对于权重百分比这一指标而言，文献［11］的聚类结果是优于文中结果的.但是就BUS 聚类规模而言，文中的聚类结果优于文献［11］.在线性函数假定下，文中联系信息流量的值优于文献［11］，这也再次说明，权重百分比不是衡量聚类方案好坏的唯一标准.

然后再将线性函数假定结果和指数函数假定结果相比较，可以得出如下几点结论.

1)虽然各项权重比随β 的变化趋势不明显，但整体来说，随着β 的增大，较大数值的权重比逐渐增大，较小数值的权重比逐渐减小，也就是说采用过大的指数区间，虽然能保证联系权重较大值的百分比，但是会给联系权重较小值的百分比带来损失，反之亦然;

2)β 对BUS 聚类规模的影响并不明显;

3)当β 采用过小或过大的区间时，聚类结果不如线性假定.聚类结果的好坏与选取合适的β有关.

总而言之，指数函数假定的聚类结果并不整体优于线性函数假定，其聚类结果的好坏取决于适当的β 值.β 的引入造成了一定次数的试算，从而增加了计算量，但是聚类算法采用指数函数有更大的灵活性.当处理某一类DSM 聚类时，可以方便地根据需要利用β 控制权重的分布情况.比如当需要保证较大的权重位于聚类内部时，可以适当牺牲较小的权重而采用较大的β.

3 船舶MDO 建模技术

文中提出的建模技术可以分为以下4 步:第1步，确定DSM 元素.在这一阶段，需要列出MDO 所有需要考虑的与设计阶段相适应的设计变量、目标和约束作为元素.第2 步，确定联系权重.以第1 步中确定的元素为基础构建DSM，并确定DSM 中每一个行列元素之间的联系权重.第3 步，聚类运算.采用指数函数假定，根据联系权重在聚类内部的百分比和BUS 聚类规模两项评价指标来确定最优聚类方案.第4 步，MDO 建模.从各个聚类中分离出各系统层的设计变量、目标和约束，建立MDO 模型.文中以一艘5400 箱集装箱船在方案阶段初期设计的概念建模为例来说明该技术.

3.1 DSM 元素的确定

DSM 中的元素包括MDO 中所考虑的设计变量、目标和约束3 类.DSM 元素的选择不仅与具体的船型有关，而且与船舶设计所处的阶段有关.虽然多学科设计优化不再是一个螺旋式前进的设计，但仍然是一个逐步细化的设计过程.在不同的设计阶段，所能考虑的元素和建模的精细程度是不一样的.一般来说，对某一具体阶段的DSM 元素选择有着两方面的要求:第一，元素要能够代表多个学科，充分体现多学科设计优化的思想;第二，所考虑的元素属于该设计阶段，而不能超越这一阶段.

本例DSM 元素根据以上两个原则及设计经验，对每一个学科分析得出.图2为传统的船舶学科分类树.

经过分析，对于5400 箱集装箱船在方案阶段初期的设计，考虑50 个元素，参见表7.

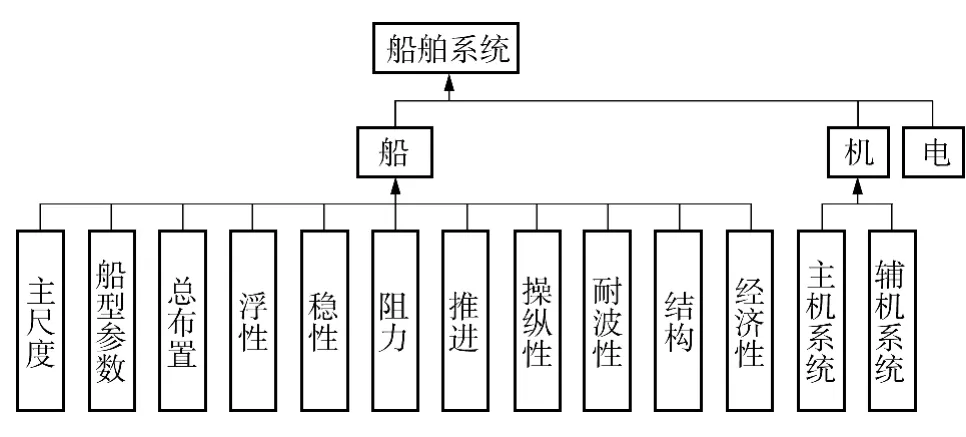
图2 传统的船舶学科分类树Fig.2 Traditional classification tree of ships

表7 各子学科元素分布表Table7 Distribution of elements in each sub-discipline

3.2 联系权重的确定

元素确定之后，再将这些元素按行列顺序依次排列，即形成一个DSM.确定船舶DSM 行列元素联系权重是一个比较困难的过程.在这一阶段，主要依靠专家经验，采用专家评估法来确定.最终得到的DSM 如表8所示.

3.3 聚类运算

为了更好地说明聚类运算的作用，首先分析传统学科划分下的MDO 模型.将表8的联系权重进行分类.设小于0.33 的联系权重为低联系权重，0.33 ～0.66 的联系权重为中联系权重，0.66 ～1.00 为高联系权重.表8的船舶DSM 共有低联系权重64 个，中联系权重429 个，高联系权重369 个.

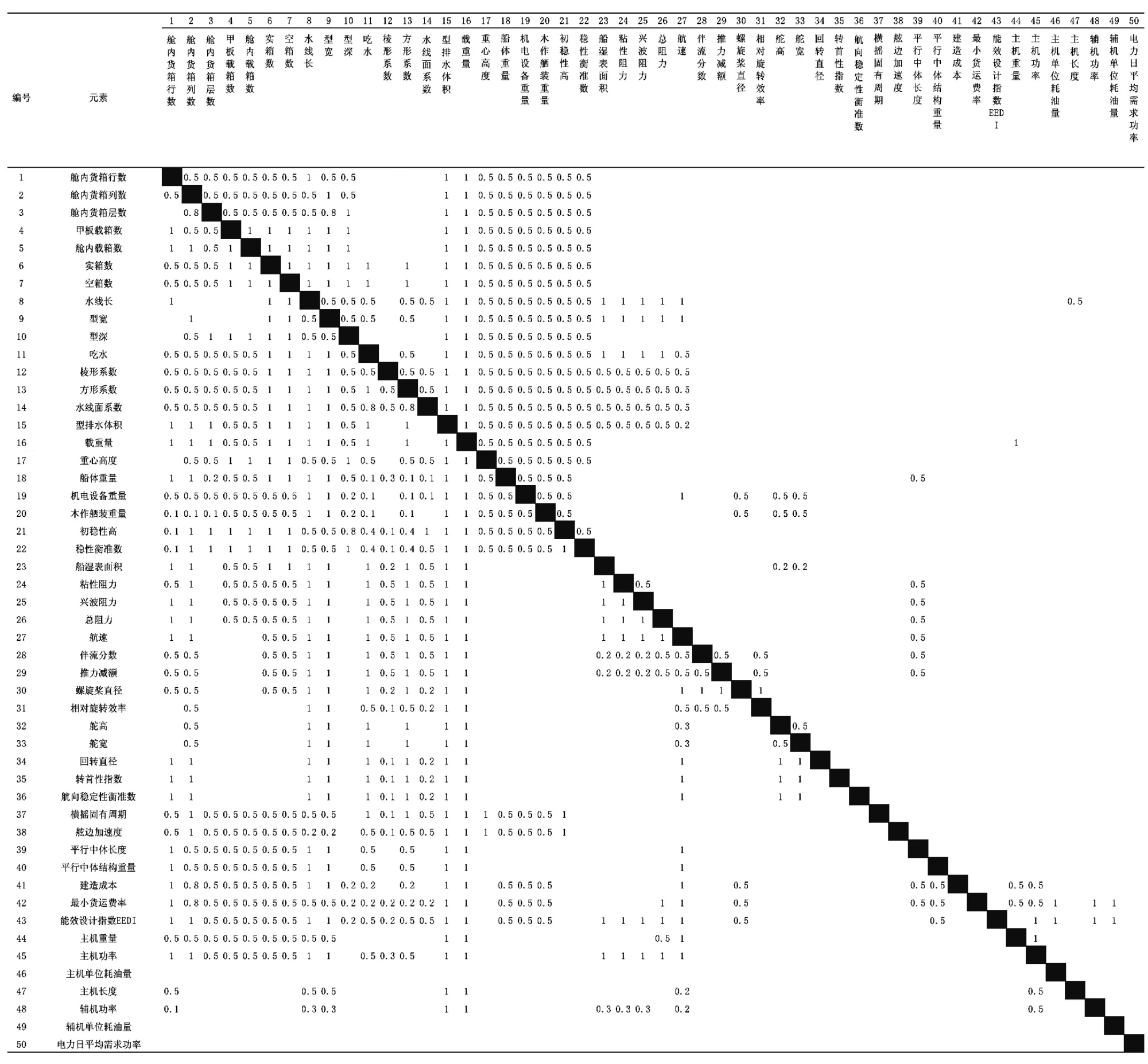
表8 船舶设计结构矩阵Table8 Ship design structure matrix

将DSM 按照图2提出的传统学科分类树进行划分，以一艘集装箱船MDO［13］为例，选择系统设计变量水线长、型宽、型深、吃水、航速和系统层目标最小货运费率作为BUS 聚类元素.除去BUS 聚类元素，其余元素都按表7的分类属于各自子学科.因此该方案共有14 个普通聚类和一个BUS 聚类.该方案在BUS 聚类规模为6 的情况下，仍有较多的联系权重位于聚类外部.这就要求MDO 不仅需要处理BUS 聚类元素和其他普通聚类之间的信息交互，还需要处理较多的普通聚类之间的信息交互.事实上，在聚类内部的低联系权重个数为15，百分比为23.44%;中联系权重个数为163，百分比为38.00%，高联系权重个数为200，百分比为54.20%.

然后采用聚类运算.由于DSM 采用0 ～1 之间的任意数字作为权重，故指数函数采用Di，j=exp(βdi，j)计算元素间的联系信息流量.种群大小设置为5000，交叉概率取0.8，变异概率取0.1，α取0.8，收敛判断值ε 取0.0001，聚类数目仍设为8.由于联系权重绝对值较小，故β 取较大值以对应相应的指数区间.β 取不同值时，得到的最优聚类方案如表9所示.

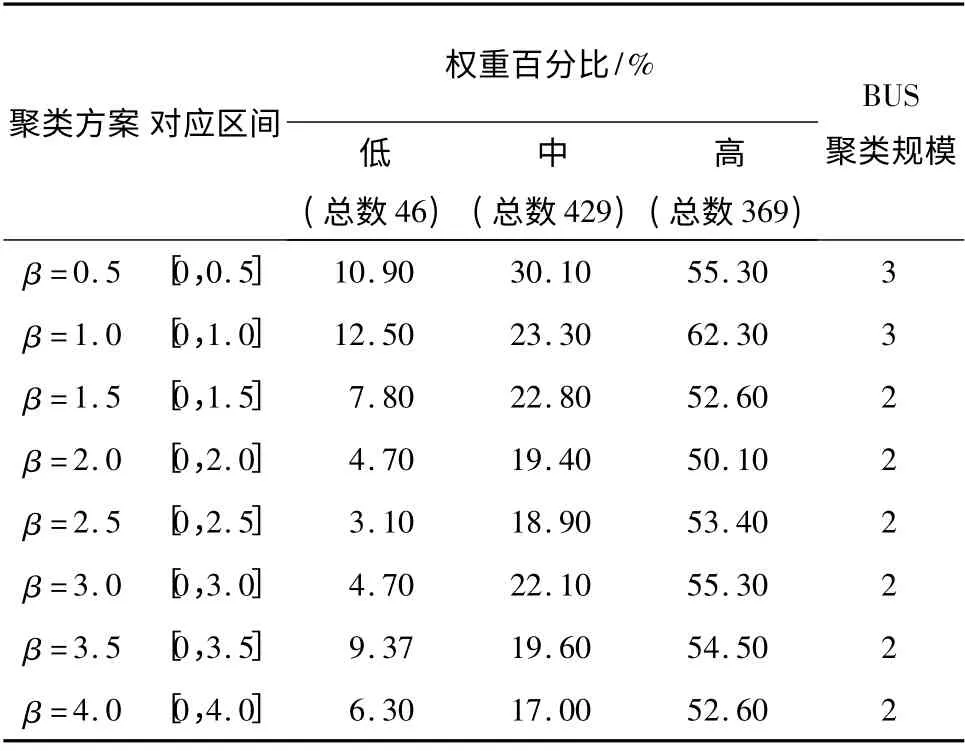
表9 船舶设计结构矩阵在不同β 下的聚类方案Table9 Optimal solutions of ship design structure matrix under different β

由上表可见，当β 大于1 时，BUS 聚类规模为2，但是联系权重的百分比比传统学科划分和线性函数假定下的聚类结果要低很多.当β 取1 时，BUS 聚类规模为3，联系权重百分比也较高，可以作为指数函数假定下的最优结果.该聚类方案如下.

1)1，2 ，18，19，20

编号对应的元素为舱内货箱行数、舱内货箱列数、船体重量、机电设备重量、木作舾装重量.

2)4，5 ，6，7，10，22

编号对应的元素为甲板载箱数、舱内载箱数、实箱数、空箱数、型深、稳性衡准数.

3)9，11 ，23，24，25，26

编号对应的元素为型宽、吃水、船湿表面积、粘性阻力、兴波阻力、总阻力.

4)3，12 ，14，17，21，37，38

编号对应的元素为舱内货箱层数、棱形系数、水线面系数、重心高度、初稳性高、横摇固有周期、舷边加速度.

5)27，39 ，41，43，44，45

编号对应的元素为航速、平行中体长度、建造成本、能效设计指数、主机重量、主机功率.

6)28，29 ，30，31，42，46，47，48，49，50

编号对应的元素为伴流分数、推力减额、螺旋桨直径、相对旋转效率、最小货运费率、主机单位油耗量、主机长度、辅机功率、辅机单位油耗量、电力日平均需求功率.

7)13，32 ，33，34，35，36，40

编号对应的元素为方形系数、舵高、舵宽、回转直径、转首性指数、航向稳定性衡准数、平行中体结构重量.

BUS:8，15，16

编号对应的元素为水线长、排水体积、载重量.

该方案与传统学科划分结果相比，BUS 聚类规模仅为传统学科划分结果的一半，高联系权重百分比也较优，只是在中低联系权重百分比上面有一定的下降.

3.4 MDO 建模

依据聚类结果建立的MDO 概念模型如图3所示.

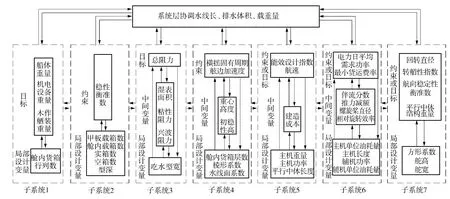
图3 概念模型Fig.3 Conceptual model

概念模型由1 个系统层和7 个子系统构成，除了系统层与各子系统之间有信息交互，各子系统之间也有信息交互.当然，子系统之间的联系大部分是低和中联系权重的信息交互.由于所处的设计阶段缺乏具体的经验公式或者CFD 计算，DSM 表中也可能包含许多不必要的联系，从而使得概念模型仍然显得比较复杂.当进入具体数学建模阶段时，该概念模型还可以对低联系权重进行进一步的简化，从而得到更加简单的MDO 数学模型.

4 结语

文中以5400 箱集装箱船在方案阶段初期的概念建模为例，说明了基于设计结构矩阵的船舶多学科建模技术.由于例子所处阶段的特殊性，文中在DSM 元素和联系权重确定方面，更多地依靠了经验分析.这些方法对于更加详细的设计阶段来说，精度显得不足，但是建模技术是可以通用的，同样可以应用于其他设计阶段.除此之外，该方法不仅仅局限于船舶学科，对于其他领域，如汽车、飞机和机械等行业也同样适用.但是，该方法在精确确定联系权重方面仍有待完善，灵敏度分析技术有望解决这一问题.

［1］钟毅芳，陈柏鸿，王周宏.多学科综合优化设计原理与方法［M］.武汉:华中科技大学出版社，2006.

［2］钱建魁.基于水动力性能的船型多学科优化设计［D］.武汉:武汉理工大学交通学院，2011.

［3］操安喜.载人潜水器多学科设计优化方法及其应用研究［D］.上海:上海交通大学船舶海洋与建筑工程学院，2008.

［4］胡志强.多学科设计优化技术在深水半潜式钻井平台概念设计中的应用研究［D］.上海:上海交通大学船舶海洋与建筑工程学院，2008.

［5］刘蔚.多学科设计优化方法在7 000 米载人潜水器总体设计中的应用［D］.上海:上海交通大学船舶海洋与建筑工程学院，2007.

［6］褚学征.复杂产品设计空间探索与协调分解方法研究［D］.武汉:华中科技大学机械科学与工程学院，2010.

［7］Christopher Gregory Hart.Multidisciplinary design optimization of complex engineering systems for cost assessment under uncertainty ［D］.Ann Arbor:The University of Michigan，2010.

［8］Nathan Andrew Good.Multi-objective design optimization considering uncertainty in a multi-disciplinary ship synthesis model［D］.Blacksburg:Department of Aerospace and Ocean Engineering，Virginia Polytechnic Institute and State University，2006.

［9］闫喜强，李彦，李文强，等.基于耦合强度和模糊设计结构矩阵的多学科解耦规划方法［J］.计算机集成制造系统，2013，19(7):1447-1455.Yan Xi-qiang，Li Yan，Li Wei-qiang，et al.Decoupling planning method of MDO based on coupling strength and FDSM［J］.Computer Intergrated Manufacturing System，2013，19(7):1447-1455.

［10］Ronnie E，Thebeau.Knowledge management of system interface and interactions forproduct development process［D］.Cambridge:Massachusetts Institute of Technology，System Design and Management Program，2001.

［11］刘建刚.并行工程中产品结构和开发过程集成管理关键技术研究［D］.南京:南京航空航天大学机电工程学院，2006.

［12］孙东川，林福永，孙凯.系统工程引论［M］.北京:清华大学出版社，2009.

［13］Ying Chen.Formulation of a multi-disciplinary design optimization of container ships［D］.Blacksburg:Department of Aerospace and Ocean Engineering，Virginia Polytechnic Institute and State University，1999.