关注学习过程 提升数学思维水平

沈建伟

在小学数学中的统计与概率这一领域，平均数、中位数、众数是小学阶段学习的三个统计量，其中以平均数应用最为广泛，它也是学生将来学习其他两种统计量的基础。

一、立足生活，紧扣学习起点，巧妙地引出“平均数”的名称和用途

【教学环节一】从比较投篮比赛的胜负问题中自然引出“平均数”。

师：小朋友们对投篮有兴趣吗？

生：有。

师：现在有两队进行投篮比赛，比赛结束后，他们争论不休，都认为自己赢了。这是两队比赛结果的统计图（如下图）。

引导学生审题后，师：男队说他们投的总数多，所以他们赢，女队说他们队的佳佳投中的最多，所以她们赢，同学们，你们觉得呢？

生1：我认为男生说的没道理，因为他们人数比女生多，比较总数投了几个是不公平的。

生2：我认为他们是一个队和另一个队比赛，不能只看其中一个人投的个数来决定的，所以我觉得女生说的是没道理的。

师：对呀！他们不是个人比赛，而是团体比赛，但总人数又不同，用什么可以代表男队的整体水平呢？用什么可以代表女队的整体水平呢？

生：用平均数。

师：平均数是什么样的数呢？你们听说过吗？

多数学生表示听说过。

师：那你们知道生活中哪些地方用到平均数吗？

生1：三年级平均每班有45人。

生2：期末考试的平均分是91分。

生3：周三中午平均每人分到6个桂圆。

师：是啊，生活中确实经常要用到平均数，出示如下信息：

生活中的平均数：

1.三（2）班学生的平均体重是25千克。

2.小红家平均每月用水5吨。

3.快速火车的平均速度是每小时350千米。

4.期中考试的班级平均分是92分。

……

在这个环节中，先从学生熟悉的投篮比赛开始，给出一个判断谁输谁赢的问题，马上激起学生热烈的讨论，在讨论中学生发现了不论是说男队赢还是女队赢都有不合理之处，教师顺势引导学生从单纯的比单人个数或集体总数的比较到比较两队的整体实力，给学生指出了一个思维的方向，即用什么来代表男队的整体水平呢？用什么来表示女队的整体水平呢？于是“平均数”呼之欲出。

二、解决问题，突出学习路径，多层次地理解“平均数”的意义和性质

理解平均数的意义和了解平均数的性质，是平均数教学的重难点，在实践教学中往往过于注重通过用什么方法求得一组数据的平均数这一手段来促使学生对平均数概念的理解，而容易忽视让学生去探究一组数据的平均数究竟和什么有关，是和各个数据的总数有关呢？还是和单个数据有关？和数据个数的多少有关系吗？如果教师不引导学生往这些方面去思考，则很少有学生会主动去思考这些问题，导致学生对平均数的意义和性质的理解过于肤浅，对将来运用“平均数”这个统计量时产生偏颇。只有经历了从直观到抽象、从感性到理性的认识过程，找到了数据的变化和平均数的变化的相关性，才能真正认识到平均数的本质特点，提高学生的思维水平。

【教学环节二】从求“平均数”的方法中初步理解“平均数”。

师：那么你们觉得平均数应该是一个怎样的数呢？

生1：不大不小的数。

生2：中间的数。

生3：很均匀的数，大家一样多。

师：你们说得都很好，第一位小朋友说是不大不小的数，是什么意思呢？

生1：就是比大的那个数小一点，比小的那个数大一点。

师：那么怎样知道这个不大不小的，大家一样多的数呢？你们有没有办法求出男生队的平均数呢？女生队呢？

多数学生觉得可以。学生思考后回答。

师生交流中，得到如下两种方法：

①移多补少。

②总数÷份数。

基于生活经验，学生对平均数已有一定的认识，但还是粗糙的、孤立的一个结果性的感性认识。教学中通过演示课件，使学生经历移多补少的过程并直观地认识到平均数的性质之一是处于这组数据的最大数和最小数之间，发现平均数不一定就是这组数据中的某一个数，而是当各数据按移多补少使得每个数据相同的规则重新分配后得到的一个新的数。在此基础上来讨论计算的方法，使“总数÷份数=平均数”这个计算平均数的数量关系式得到直观的支撑，便于学生理解为什么平均数可以用总数除以份数的方法求得，并有别于“总数÷份数=每份数”这个已有的认识。

【教学环节三】从数据的变化中深入理解“平均数”。

师：女生队的平均数是5个，如果“小华”没有参加的话，你认为女生队的平均数会有变化吗？会怎么变？

生：会的，平均数会变大。

师：为什么？为什么少了一个人，平均数反而变大了？

生：因为女生中小华投的个数最少，需要补给她3个才和大家一样多，但如果她不参加的话，那佳佳的3个可以补给小丽和小雨，每个人的个数就多了。

师：是这样吗？

学生表示赞同。通过课件演示，展示移多补少的过程，并列式为：（5+7+9）÷3=7（个）

师：那么，如果“小华”仍旧参加，而“佳佳”没有参加呢，女生队的平均数又会怎样呢？

生：平均数会变小，因为佳佳投得最多，她如果不参加的话，女生队很吃亏，总成绩肯定会变差的。

师：你说的总成绩变差是指他们投中的总个数少了吗？

生：不是总个数，是她们队的平均数少了。

师：那为什么平均数就会少了呢？

生：因为她会把多余的个数分给别人，如果她不参加，小华和小雨就达不到6个了。

通过课件演示，展示移多补少的过程，并列式为：（7+3+5）÷3=5（个）

师：从刚才的两个事情中，你觉得平均数的大小是由什么决定的呢？

生：平均数的大小是由投的最多的和最少的个数决定的。因为去掉了最大的数，平均数就变小了，去掉了最小的数，平均数就变大了。

师：他说的有道理吗？有不同的想法吗？

生：我觉得除了最大数和最小数以外，其他的数如果改变的话，平均数也要变化的。

师：比如说……

生：如果小雨再多几个的话，他们本来已经分好了6个，那小雨多几个的话又可以分到每个人那里了，就比6个多了。

师：他说的有道理吗？

学生同意。

师：也就是说，平均数和这些数据中的每个数都是有联系的，每个数的变化都会影响平均数的大小。

师：同学们，如果告诉你男生队有一个人没参加，但他们的平均数还是5个，你相信吗？

生1：不相信，因为平均数是要变化的。

生2：可以的，如果小星没参加的话，平均数是不变的，因为他本来就是5个，不用分给别人，也不用从别人那里加过来。

生3：丁丁也可以的。

师：这又是什么原因呢？这一次数据的变化为什么没有影响平均数呢？

生：因为他们和平均数是一样的。

在经历了如此的数据变化，学生体会到平均数不是一个孤立的数，而是由一组数据中每个数的大小来决定的，真正认识到平均数代表的是一组数据的一个整体水平，理解平均数作为一个统计量的意义所在。在这个学习过程中，教师先通过对一组数据中个别数据的改变，引导学生发现一个数据的变化，导致了这组数据平均数的变化，进而再通过巧妙的提问使学生发现和平均数相等数据和平均数的关系。聪明的学生也许还会想到和平均数相差越大的数对平均数影响越大，与平均数越接近的数对平均数影响越小。移多补少的数学方法在帮助学生理解平均数的性质上起到了支撑学生思维的良好作用，以它直观的表象促使学生发现一组数据内在的关联，使学生的思维从外在的形象思维逐渐地转换到内在的抽象思维，在思维水平上提升到了一个新的高度。

三、多元练习，培养判断能力，形成求平均数的技能

【教学环节四】快速地说出下列每组数据的平均数：

①7、8、9 ②88、90 ③9、0、21 ④10、20、30、20

⑤75、80、85 ⑥13、7、40 ⑦10、64、16

在平均数教学中，理解平均数的意义和性质固然重要，同时准确地求得某组数据的平均数的能力也是必不可少的。那么，如何避免在求平均数的练习中产生枯燥感和机械性，如何在求得平均数的过程中获得数学思维能力的提升，感受数学方法的灵活性。这是提高课堂有效性和提高学生学习兴趣所必须思考的问题。从前面的学习中，学生掌握了“移多补少”和“总数÷份数=每份数”两种方法去求得一组数据的平均数。但当真正面对一组数据时，学生会怎想呢？他会优先考虑哪种方法呢？如何引导学生去思考运用哪种方法呢？笔者通过巧妙的习题设计，数据从特殊到一般，让学生在“速算比赛”这样的有一定压力和容易兴奋的思维状态下，自觉地取舍两种不同的方法，教师适时地进行点拨和反问，使学生能在较短时间内从数据的特征上发现求平均数的适当方法。通过这样的练习，不仅对平均数的意义和性质有一定的强化作用，而且也训练了求平均数的技能，更重要的是学生在从看到数据到得到答案的过程中，他的观察能力、判断能力得到了良好的培养，提高思维的具体化和系统化能力。

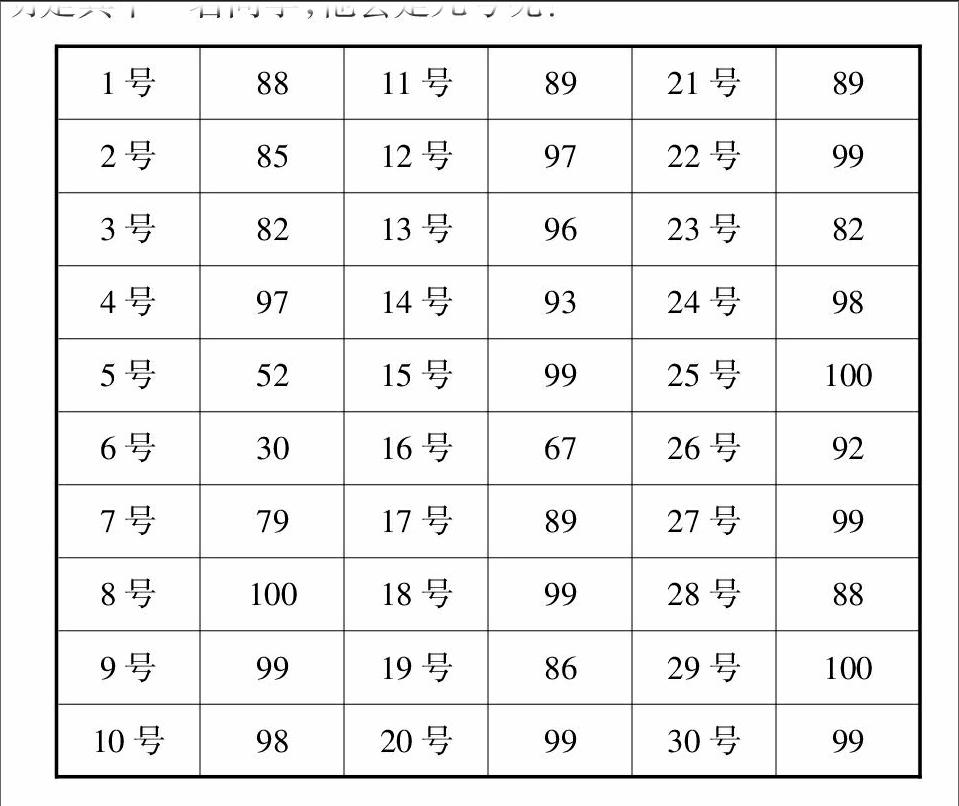
【教学环节五】如下表，302班期末测试，班级平均分是89分，小明是其中一名同学，他会是几号呢？

生1：11号。

生2：17号、21号都是89分，也有可能。

师：你们同意吗？还有别的可能吗？一定是89分吗？

生：我觉得不一定要89分，其他的也可以。

师：为什么？

生：因为平均数是89分，小明不是89分，平均数也可以是89分的。

师：那你觉得在这里这个平均数89分应该用什么方法求出来呢？

生：用全班的总分除以30就可以求出来。

师：好。[课件演示2670÷30=89（分）]电脑帮我们算出总分是2670分，为什么小明不是89分也可以，他是其他的分数，平均数会改变吗？

生：不会，因为总分没变。

师：哦，原来是这样，总分不变，这组数据的平均数就不会变。那反过来这样想对不对：一组数据的平均数是89，但数据中可以有比89大的数，也可以有比89小的数？

生：对。

在前面的学习中，学生通过对一组数据的观察分析，理解了平均数的意义和性质，如果用符号“▲”来表示这组数据，用符号“■”表示这组数据的平均数的话，学生的思考顺序可以表示为“▲→■”，那么在这个习题中，学生首先知道的是一组数据的平均数，而后要他推导出其中某个数据，这个思考顺序应该为“■→▲”，而且这个数据并不是确定的，而是可以使不大于100的任何自然数。这样的思维训练在数学教学中是经常要用到的，这种思维的方式可以帮助学生解决很多数学推理问题。这样既可以锻炼学生思维的严密性，还可以培养思维的发散性。在解决实际问题时，学生还会碰到类似“小河的平均水深1.3米，淘气身高1.5米，他能安全的过河吗？”之类的问题。其实是可以回归到以上问题中去的，平均分89分相对于平均水深，而每个同学的得分相对于小河不同位置的水深，这些位置的水深是不确定的，可能比1.5米还深。通过这样的比较和解释，学生自然能够理解过河的实际问题了。

参考文献：

邹敏.“平均数”两次教学实践对比与反思[J].小学教学设计，2010（17）.

？誗编辑 温雪莲