*利用局部性质刻画三角环上的导子
2015-12-17王彩莲侯晋川太原理工大学数学学院太原030024
王彩莲,侯晋川(太原理工大学数学学院,太原030024)
*利用局部性质刻画三角环上的导子
王彩莲,侯晋川
(太原理工大学数学学院,太原030024)
摘 要:证明了当三角环U满足某些条件时,三角环中的每个元都是可加拟Jordan全可导点。作为推论,有非平凡可补元的Banach空间套所对应的套代数中的每个算子都是可加拟Jordan全可导点。
关键词:导子;拟Jordan全可导点;三角环;套代数
令R是一个环(代数)。可加(线性)映射Φ:R →R被称为是可加(线性)导子,如果Φ(xy)=Φ(x)y+xΦ(y)对所有的x,y∈R都成立。线性导子通常简称为导子。记x°y=xy+yx为x,y的Jordan积。可加映射Φ:R→R被称为可加Jordan导子,如果Φ(x°y)=Φ(x)°y+x°Φ(y)对所有x,y∈R均成立。线性Jordan导子也可以类似的定义。显然,(可加)导子一定是(可加)Jordan导子,另一方面,在特征不是2的半素环上每个Jordan导子都是导
子[1-2]。
近年来,许多学者通过映射的局部特征来刻画导子和Jordan导子。令g∈R.称可加映射Φ:R→R 在g点可导,如果Φ(xy)=Φ(x)y+xΦ(y)对所有R中满足xy=g的x,y都成立。类似地,称可加映射Φ:R→R在g点Jordan可导,如果Φ(x°y)=Φ(x)°y+x°Φ(y)对所有R中满足x°y=g的x,y均成立。g被称为R的一个全可导点,如果每个在g点可导的可加映射都是可加导子。同样地,g被称为R的一个Jordan全可导点,如果每个在g点Jordan可导的可加映射都是可加Jordan导子。已有的研究成果表明,对任意环来说,0既不是全可导点,也不是Jordan全可导点[3-4]。但是,对某些环或者代数来说,存在许多非零的全可导点。但对于Jordan全可导的例子,知道的很少。在文献[4]中证明了单位元I是包含非平凡幂等元的素Banach代数,因子von Neumann代数及某些三角环和套代数上的一个Jordan全可导点。
三角环(代数)概念在文献[5]中第一次提出,随后,许多学者进行了深入研究。令A和B是两个单位元分别为IA和IB的环(代数),M是一个忠实的左A-模,同时也是忠实的右B-模;记
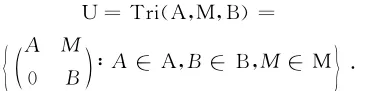
于是在通常的矩阵加法和乘法运算之下U是一个环(代数),称之为由A,M,B构造的三角环(代数)。注意三角环(代数)既不是素的也不是半单的。
除讨论在某点可导或Jordan可导的映射结构以及与导子或Jordan导子的关联问题,许多学者还讨论具有如下局部可导行为的映射。设Φ:R→R为可加映射。对于给定的元g∈R,如果
Φ(x°y)=Φ(x)°y+x°Φ(y).(1)
对所有满足xy=g的x,y∈R都成立,则称Φ在g点是拟Jordan可导的。g∈R被称为是R中的拟Jordan全可导点,如果每个在g点拟Jordan可导的可加映射都是导子。注意Φ在g可导并不能推出Φ 在g点是拟Jordan可导的,在某一点拟Jordan可导以及拟Jordan全可导点也被称为在某点Jordan
可导及Jordan全可导点[7-11]。这有时会引起与引言部分中第二段所述的Jordan可导点和Jordan全可导点的标准概念相混淆。
以下列举与本文相关的一些结果。2009年,文
(Tel)15536888410
通讯联系人:侯晋川,教授,博导,(E-mail)jinchuanhou@aliyun.com献[9]证明了单位算子是B(H)上的拟Jordan全可导点。2010年,文献[10]证明了上三角矩阵中的每一个元都是拟Jordan全可导点。
笔者在比较弱的条件下,证明三角环(代数)上的每一个元都是拟Jordan全可导点。作为应用得到:含有非平凡可补元的Banach空间套所对应的套代数中的每个点都是该套代数的可加拟Jordan全可导点。以下是本文的主要结论。
定理 令U=Tri(A,M,B)是一个三角环,其中A和B是两个单位元分别为IA和IB的环,M是一个忠实的左A-模,同时也是忠实的右B-模;如果
a)2IA和3IA在A(2IB和3IB在B)中可逆;
b)对每个A∈A(B∈B),存在正整数nA(nB)使得nAIA-A(nBIB-B)在A(B)中可逆;
c)对A∈A及B∈B,若AM=MB对每个M∈M都成立,则或者A=0或者A可逆且是IA的倍数。
那么,U中的每个元都是拟Jordan全可导点。
1 主要结果的证明
以下给出定理的证明。
令G∈U.假设Φ:U→U是在G点拟Jordan可导的可加映射。往证Φ是可加导子。
因为Φ是可加的,所以存在可加映射fR:R→A,gR:R→B以及hR:R→M,(其中R=A,M,B),使得

0 0是如下定义的内导子:Ψ(X)=[X,T0]=XT0-T0X对所有X∈U都成立。如果必要,用Φ+Ψ代替Φ,则下面可以假设hB(IB)=0。
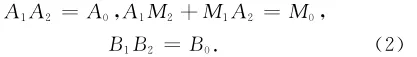
因为Φ:U→U是可加的并且在G点拟Jordan可导,故有.
这表明


以及
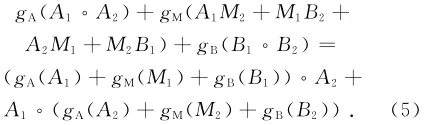
断言1 fA和gB分别在A0和B0拟Jordan可导。
为证明fA在A0点拟Jordan可导,需要证明对任意A中满足XY=A0的X,Y,fA(X°Y)=fA(X)°Y+X°fA(Y)。
先给出一个事实。
事实如果A,B,C∈A(或者A,B,C∈M)对所有满足rIA在A中可逆的正整数r都有r2A+rB+C=0成立,则A=B=C=0。
实际上,由定理假设(a),可以取r=1,2,3,于是有
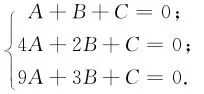
由前2个方程,可得B=-3A,C=2A.代入第3个方程立得C=2A=0,从而A=(2IA)-12A=(2IA)-10=0以及B=-3A=0.
在下面的论证中,该事实会被多次用到。
假设X,Y∈A满足XY=A0.对任意满足rIA可逆的正整数r,取A1=r-1X=(rIA)-1X,M1=M0,B1=B0,A2=rY,M2=0,B2=IB,由式(3)有

等价地有,
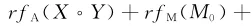
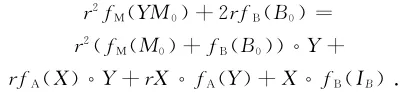
因此由前面的事实,有
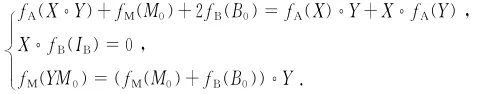
取X=IA,Y=A0并代入最后一个关系式,得fB(IB)=0.再令Y=IA,X=A0,有fM(M0)+2fB(B0)=0.所以,fA(X°Y)=fA(X)°Y+X°fA(Y).因此,fA在A0点拟Jordan可导。
同理可证:gB在B0拟Jordan可导。
断言2 fM=0,fB=0,gA=0以及gM=0.
只要证明对任意的A∈A,B∈B和M∈M都有
fM(M)=0=fB(B),gA(A)=0=gM(M).由断言1,当XY=A0时,有fA(X°Y)=fA(X)°Y +X°fA(Y).所以,式(3)变为

对任意的M∈M,取A1=rIA,M1=M0-rM,B1=B0,A2=r-1A0,M2=M,B2=IB并将其代入式(6),其中r是任意满足rIA可逆的正整数,从而有

这就表明2fM(M)=0.注意到,由假设a),2IA在A中可逆,因此必有fM(M)=0.
对任意可逆元B∈B,取A1=IA,M1=0,B1=rB0B-1,A2=A0,M2=M0,B2=r-1B并将其代入式
(6),其中r是任意满足rIB可逆的正整数。从而可以得到
fB(B0B-1°B)=rfB(B°B-1)°A0+2r-1fB(B).这就说明2fB(B)=0,因此fB(B)=0对于所有可逆元B∈B都成立。现在设B∈B为任意元。由假设b),存在正整数n使得nIB-B是B的可逆元。所以,由刚刚证明的结论,有fB(nIB-B)=0.又fB(nIB)=nfB(IB)=0,所以有fB(B)=0对任意B∈B都成立。同样,由式(3)和式(4)可以得到gA(A)=0=gM(M)对所有A∈A以及M∈M都成立。
断言3 hA=0,hB=0.
需要证明,对任意的A∈A和B∈B都有hA
(A)=0=hB(B).
注意到已经假设了hB(IB)=0.对任意可逆的A∈A以及任意使得rIA和rIB可逆的正整数r,取A1=A,M1=rM0(=(rIA)M0=M0(rIB)),B1=rB0,A2=A-1A0,M2=0,B2=r-1IB并将其代入式(4).则可以得到

由前面的事实易知hA(A)=0.因此,证明了hA在所有可逆元上都为0.考虑任意的A∈A.由定理假设b),存在正整数n使得nIA-A是可逆的。于是hA(nIA-A)=0且有hA(nIA)=nhA(IA)=0.这就表明hA(A)=0对所有A∈A都成立。同理,利用式(4)也可以得到hB(B)=0对所有B∈B都成立。
断言4 对任意A∈A,M∈M以及B∈B,都有
hM(AM)=fA(A)M+AhM(M)-AMgB(IB),hM(MB)=hM(M)B+MgB(B)-fA(IA)MB.
(7)
对任意可逆元B∈B,任意的M∈M以及任意的使得rIB在B中可逆的正整数r,取A1=IA,M1=M,B1=r-1B0B-1,A2=A0,M2=M0-rMB,B2
=rB并将其代入式(4)可得
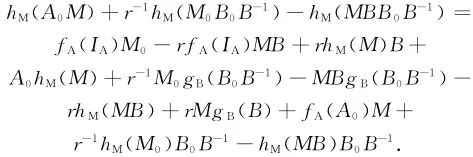

利用与上面相同的方法易证对所有M∈M以及B中可逆的B都成立。令
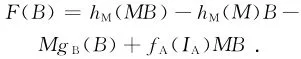
则F∶B→M是一个可加映射,并且F(B)=0对所有可逆的B∈B都成立。由假设b),对任意的B∈B,存在正整数n使得nIB-B是可逆的。所以,由前面的论述,有F(nIB-B)=0.因为F是可加的,F (nIB)=nF(IB)=0,所以,对任意的B∈B,都有F (B)=0.于是
hM(MB)=hM(M)B+MgB(B)-fA(IA)MB对所有M∈M及B∈B都成立。同理,对任意可逆元A∈A,任意的M∈M,以及任意满足rIA在A中可逆的正整数r,在式(4)中取A1=rA,M1=M0-rAM,B1=B0,A2=r-1A-1A0,M2=M,B2=IA,则
有,hM(AM)=fA(A)M+AhM(M)-AMgB(IB),对所有M∈M及可逆的A∈A都成立。用与上面相同的论证,可以得到对所有的M∈M以及A∈A都成立。
断言5 对任意A∈A,M∈M以及B∈B都有

先假设G≠0.由断言4的论证,只需要证明fA(IA)=0以及gB(IB)=0.将A=IA代入式(7),得到fA(IA)M=MgB(IB)对所有M∈M均成立。由假设c),对A∈A及B∈B,AM=MB对所有M∈M都成立,则或者A=0或者A可逆,且是IA的倍数,不妨设A=αIA.显然,由A=0可以得到B=0;由A=αIA可以得到B=αIB.因此,如果允许α=0,则fA(IA)=αIA以及gB(IB)=αIB.所以,
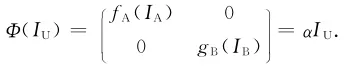
因为Φ在G点拟Jordan导,所以,

因此,Φ(IU)°G=0,从而2αG=0.如果α≠0,则αIU是可逆的,从而G=0,与G≠0矛盾。所以必有α=0,即fA(IA)=0且gB(IB)=0.
现假设G=0.对任意的M∈M,A∈A,取A1=0,M1=M,B1=0,A2=A,M2=0,B2=0.将其代入式(4).因为Φ在G=0点拟Jordan可导,容易验证
hM(AM)=fA(A)M+AhM(M)
仍然成立。类似可得
hM(MB)=hM(M)B+MgB(B)
对所有M∈M和B∈B都成立。
断言6 fA和gB都是可加导子。
应用断言5,有
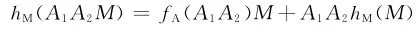
对所有A1,A2∈A,M∈M都成立。另一方面,
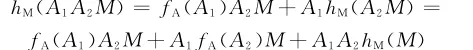
对所有A1,A2∈A,M∈M都成立。因为M是忠实的左A-模,从上述两个关系式可推得
对所有A1,A2∈A都成立。因此,fA是可加导子。类似可以验证gB也是可加导子。
断言7 Φ是可加导子。
需要证明Φ(XY)=Φ(X)Y+XΦ(Y)对所有XY∈U都成立。
由断言1-6,有
其中fA和gB都是可加导子,并且
hM(AM)=fA(A)M+AhM(M),
hM(MB)=hM(M)B+MgB(B).
对所有A∈A,M∈M及B∈B都成立。对任意X=A1M10 B
烄烆
烌烎1以及Y=A2M20 B
烄烆
烌烎2
,
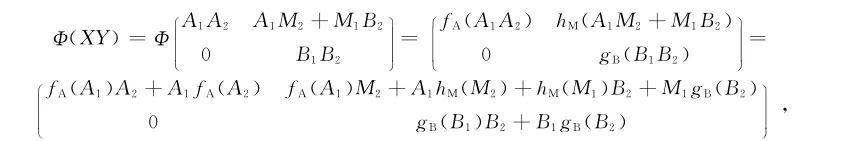

而).
所以Φ是一个可加导子。证毕。
作为应用,考虑Banach空间套代数的情形。用B(X)表示Banach空间X上有界线性算子全体。
推论 设N是一个在实或复Banach空间X上的非平凡套,令AlgN是与之相应的套代数。假设存在N∈N\{0,X}使得N在X中可补。令Φ:AlgN →AlgN是可加映射,且G∈AlgN.若Φ(X°Y)=Φ (X)°Y+X°Φ(Y)对所有满足XY=G的X,Y∈AlgN都成立,则Φ是一个可加导子;进而,当dim X=∞时,存在算子T∈B(X)使得Φ(A)=AT-TA对所有A∈AlgN都成立。
证明 因为存在非平凡的元N∈N可补,所以存在幂等元E∈AlgN使得E的值域是N.从而N1=E(N)和N2=(I-E)(N)分别是N和ker E上的套。此外,AlgN1=EAlgNE,AlgN2=(I-E)AlgN (I-E)并且AlgN可以看做是一个三角代数。
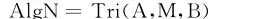
其中A=AlgN1,B=AlgN2,M=EAlgN(I-E)=B (ker E,N),即ker E到N的有界线性算子全体。显然AlgN满足定理的条件a)-b)。为证明它满足条件c)假设A∈A和B∈B使得AM=MB对所有M ∈M=B(ker E,N)都成立。特别的,Axf=xfB=xB*f对所有秩一算子xf都成立,其中,x∈N且f∈(ker E)*=N⊥,N⊥为N的零化子。从而,存在数λx使得Ax=λxx对每个x∈N都成立。而此蕴涵存在常数λ使得A=λIN=λIA.显然也有B=λIB.现在,由于Φ在G点拟Jordan可导,由定理,Φ是一个可加导子。另外,如果dimX=∞,则AlgN上的每个可加导子都是线性的,从而是内的[12]。从而存在T∈B(X)使得Φ(A)=AT-TA对所有A∈AlgN都成立。证毕。
参考文献:
[1] Bresar M.Jordan derivations on semiprime rings[J].Proc Amer Math Soc,1988,104(4):1003-1006.
[2] Herstein I.Jordan derivations of prime rings[J].Proc Amer Math Soc,1957,(8):1104-1110.
[3] Jiao M Y,Hou J C.Additive maps derivable or Jordan derivable at zero point on nest algebras[J].Lin Alg Appl,2010,432 (11):2984-2994.
[4] An R L,Hou J C.Characterizations of Jordan derivations on rings with idempotent[J].Linear and Multilinear Algebra,2010,58(6):753-763.
[5] Cheung W S.Commuting maps of triangular algebras[J].London Math Soc,2001,63(1):117-127.
[6] Cheung W S.Lie derivations of triangular algebras[J].Lin Mult Alg,2003,51(3):299-310.
[7] Qi X F,Hou J C.Additive Lie(ξ-Lie)derivations and generalized Lie(ξ-Lie)derivations on nest algebras[J].Linear Algebra Appl,2009,431(5):843-854.
[8] Zhang J W,Yu W Y.Jordan derivations of triangular algebras[J].Linear Algebra Appl,2006,419(1):251-255.
[9] Jing W.On Jordan all-derivable points ofB(H)[J].Linear Algebra Appl,2009,430:941-946.
(编辑:刘笑达)
[10] Zhao S,Zhu J.Jordan all-derivable points in the algebra of all upper triangular matrices[J].Linear Algebra Appl,2010,433 (11):1922-1938.
[11] Zhu J,Xiong C P,Zhang L.All-derivable points in the algebra of all upper triangular matrices[J].Linear Algebra Appl,2008,429(4):804-818.
[12] Han D G.Additive derivations of nest algebras[J].Proc Amer Math Soc,1993,119(4):1165-1169.
Characterizing Derivations on Triangular Rings by Local Properties
WANG Cailian,HOU Jinchuan
(College of Mathematics,Taiyuan University of Technology,Taiyuan030024,China)
Abstract:Under some mild conditions on triangular ring U,every element of Uis an additive quasi Jordan all-derivable point.As a corollary,for Banach space nest with nontrivial complement elements,every operator of the corresponding nest algebras is also an additive quasi Jordan all-derivable point.
Key words:derivations;quasi Jordan all-derivable points;triangular rings;nest algebras
作者简介:王彩莲(1989-),女,山西吕梁人,硕士生,主要从事算子理论与算子代数研究,(E-mail)wangcailian1224@163.com,
基金项目:国家自然科学基金资助项目:算子空间上一般保持问题及在量子信息理论中应用研究(11171249)。
收稿日期:*2014-10-15
DOI:10.16355/j.cnki.issn1007-9432tyut.2015.03.023
文献标识码:A
中图分类号:O177.1
文章编号:1007-9432(2015)03-0361-05
