几何直观在低段数学教学中的运用

戴巧凤

几何直观是《义务教育数学课程标准（2011年版）》（以下简称《课标》）中新增出来的一个重要理念。在《课标》中指出：几何直观主要是指利用图形描述和分析问题。借助几何直观可以把复杂的数学问题变得简明、形象，有助于探索解决问题的思路，预测结果。几何直观可以帮助学生直观地理解数学，在整个数学学习过程中都发挥着重要作用。很显然《课标》对“几何直观”在教学中的作用是很重视的，它在整个小学乃至初中的学习中都发挥着重要作用。几何直观有哪些有效策略已经成为数学教学方式中的一个关注问题。尤其是在小学低年级的课堂教学中，借助有效的策略方法，更能符合学生的认知思维和发展，有助于让学生在抽象思维学习中有更直观的认识，更好地描述和分析问题。

策略一：在画图中培养几何直观

在平时的教学中，我们会发现学生对题意理解不透彻、不全面的现象，特别是一年级的学生，他们考虑问题不全面，往往是想到了这个就忘了那个。如，在一年级练习中有这样两道题目：

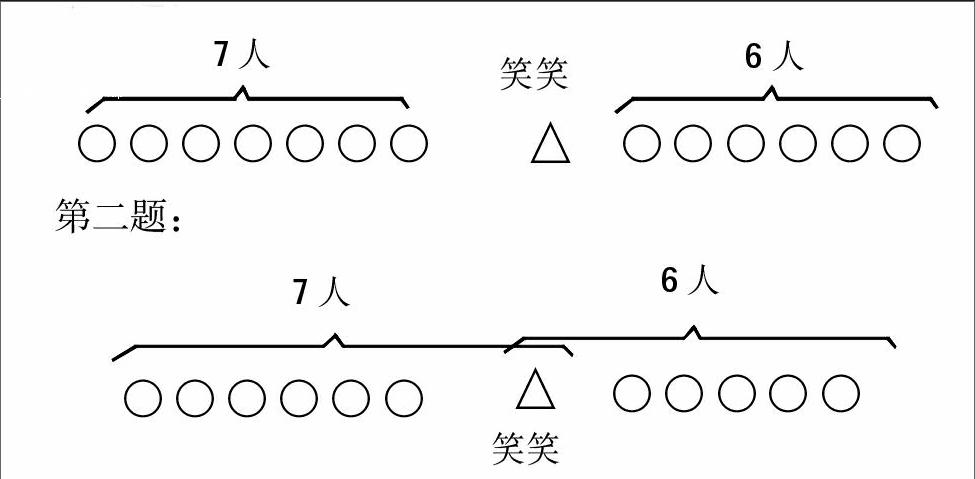
（1）笑笑的前面有7个小朋友，后面有6个小朋友，这一排一共有几个小朋友？

（2）从前面数笑笑排在第7个，从后面数笑笑排在第6个，这一排一共有几个小朋友？

这两类题目总是有学生做错，有的学生直接就是7+6=13，而有的学生对于到底是该加1还是减1，根本不清楚，无论教师说了多少遍可还是一知半解。这个时候我们可以教学生用画图的方法来思考解决问题。

第一题：

第二题：

借助直观图形展现出排队的情况，学生一目了然，很容易列出算式，使复杂的问题简单化。在这个过程中，我们教师还要引导学生体会示意图对解决这个数学问题的重要作用，感受画图策略的价值。让学生在不断的学习中积累经验，丰富解决问题的方法。以几何直观图形作为桥梁，分析题中的数量关系，从而解决数学问题。

策略二：自建模型中发展几何直观

不同的教学内容，教师要创造性地使用教学，适时利用实物和模型为教学服务，因为实物和模型承载着很多数学信息，需要学生去观察，去探索，而自建模型是让学生在自建中去发现其中的规律，从而总结出方法。如下题：

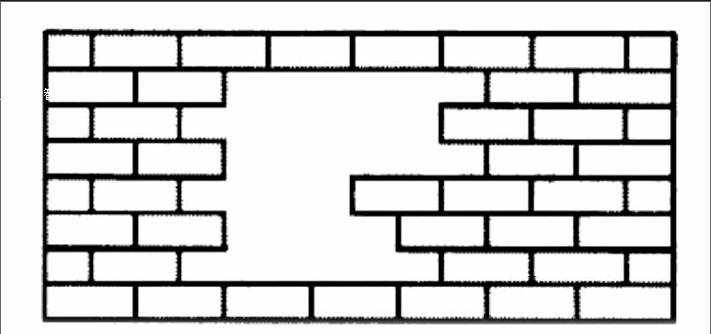
画一画，数一数，墙上缺了（ ）块砖。

这一题在一年级的数学练习中经常出现，可是每次没有几个孩子是做对的，而做对的都是能画得出来的几个小朋友，无论我用什么方法，孩子们收获总是甚微，和他们说第一层砖和第二层砖要错开，可是学生画的时候，总是把他们整齐地画出来，以至于砖的大小不同，答案也五花八门。为此，我在思考，我要怎样教学生才能真正明白呢？讲台上的一本新华字典让我豁然开朗，何不让学生亲身经历一下砌墙呢？让学生自己来建一面模型墙。38个学生，一人一本新华字典，就相当于有38块砖。我先在电脑上展示几面墙的图片，让学生观察，然后让学生逐个到上面来把自己的砖砌上去，这种活动探究的方式，学生的兴趣很高，一旦有个学生把砖放错了，其他学生就会马上帮他指出来，为什么放错了，应该怎么放。通过这样的直观感受，动手实践，既形象生动，又给学生留下了深刻印象。

策略三：教学中渗透几何直观

学生最先认识的是形，从他会拿笔的时候，他先画出来的是线、点和一些不规则图形，刚入幼儿园时，他们都很喜欢画画，所以先深入学生脑中的是形。而到了小学一年级，我们在教学时往往会让学生脱离这直观的图形去思考问题，忽略了用几何直观去思考数学问题，其实这更符合学生的认知规律。

有专家说：“如果一个特定的问题可以转化为一个图像，那么就整体地把握了问题。”学生如果能用图形把一个实际问题描述清楚，就可使复杂的问题变得简单，更容易展开形象思维。可是有时候这能用图形就可以把一个问题描述的很清楚，学生却很少会想到。这其实与我们教师的平时教学有很大关系。在平时的教学中，遇到问题老师往往只是让学生想一想，想不出来题目再读一读，或者与同桌讨论交流，却很少会让学生根据题意在纸上画一画或借助实物做一做，以至于让学生遇到问题就在脑子里想，却怎么也想不出来。如果在平时教学就不时渗透学生用一些简单的图形和符号来表示题意，学生就能更易于理解，有时讲不清、道不明，看图却能很明了。直观，它不仅仅只局限于几何直观，有的学生画圆圈，有的学生画三角形，有的学生画竖线条，只要是能够理解的，都是他的直观。如果学生能够用自己的方式直观地表现，具备这种解决问题的思维方式，掌握这样的方法，是一种意识的体现，也为几何直观能力的形成打下了良好基础。

运用几何直观解决数学问题，是2011年版新课标的要求，也是提高学生素质的要求。在教学中要长期关注，并有意识地渗透，潜移默化地润入孩子心间。作为教师，要及时捕捉、合理应用，让学生感受其在数学学习中的作用，感受几何直观的优势，逐渐把它转化为数学学习的内在需要。

编辑 孙玲娟