让数学成为学生的朋友

卢枫

数学总是蕴藏着很深的魅力，教数学，往往不仅仅是把数学知识教给学生，更重要的是给学生学习数学的感觉，这种感觉可以是疑惑，可以是兴趣，可以是突变的思维转折，也可以是久思之后的茅塞顿开。总之，如果能让学生扎进去，学生自然不会排斥这门学科，这一点很重要。

教授初一课程，我接触的都是刚刚入学初中的孩子，七年级数学教材的第一章安排的是《生活·数学》，目的就是让学生能联系生活了解数学，而一般第一节课，我总是在和学生聊天。聊什么呢？围绕数学来聊，从一个这样的问题开始。我告诉他们，老师也是从一个偶然的问题开始对数学产生兴趣的：“一段楼梯，有15节台阶，规定：每次只能走1节或者2节楼梯，要想走完这段楼梯，一共有多少种不同的方法？”问题抛出，总有一些学生会很快举手，有“5种”“6种”等等这样的答案，而一些沉稳的学生，会细细思考后反驳一下刚才同学的回答。讨论之后，大家慢慢就发现了方法很多，很难数出来。这时，其实学生已经陷入深思了，这也正是教学最好的时候。所以，我就鼓励他们：“解决数学问题，需要适合的方法；问题还需要从基础模型开始建立思考。”

“既然大家觉得15节台阶方法太多，不能列举，那么我们假设如果只有1节台阶，情况会如何？”这时候学生就开始和我一起列举了。

1节 1 方法：1种

2节 1/1 或 2 方法：2种

3节 1/2 或 2/1 或1/1/1 方法：3种

4节 2/2 或 2/1/1 或 1/2/1 或 1/2/2 或 1/1/1/1 方法：5种

5节 2/2/1或2/1/2或1/2/2或1/1/1/2或1/1/2/1或1/2/1/1或2/1/1/1或1/1/1/1/1

方法：8种

……

当学生按照顺序列举后，细心的学生很快就发现了规律：“方法数的规律是后面的一个数字是前面两个数字的和”。学生很快就计算出来15节台阶的方法数是987。

学生都非常惊叹，竟然有这么多种方法。如果用列举的方法来写，根本写不完。这就是一个从简单模型到复杂模型的过渡，学生们都叹服，原来数学是这样的。我会再补充一些关于斐波那契数列的知识，学生听得津津有味，对数学的兴趣不言而喻。

数学的魅力总是在时间轴上一些细微的地方闪现，而学生很少能注意到这当中的一些联系，下面的这个例子我觉得系统地讲给学生非常棒：

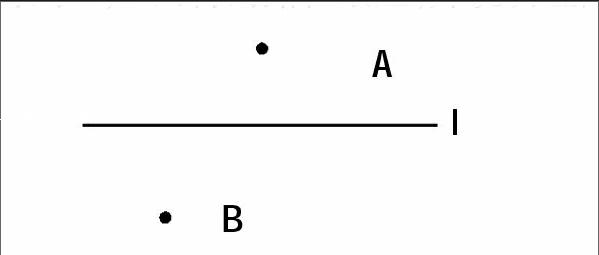
这是初一下学期的一道习题：有条小河l，点A，B表示在河两岸的两个村庄，现在要建造一座水站向两个村庄供水，请你找出水站P的位置，使得到A，B两村的路程最短，并说明理由。

分析：初一的学生面对这个问题，并不难，学生也很容易地找到了答案：连接A、B两点即可，给出的理由是小学学过的“两点之间，线段最短”。

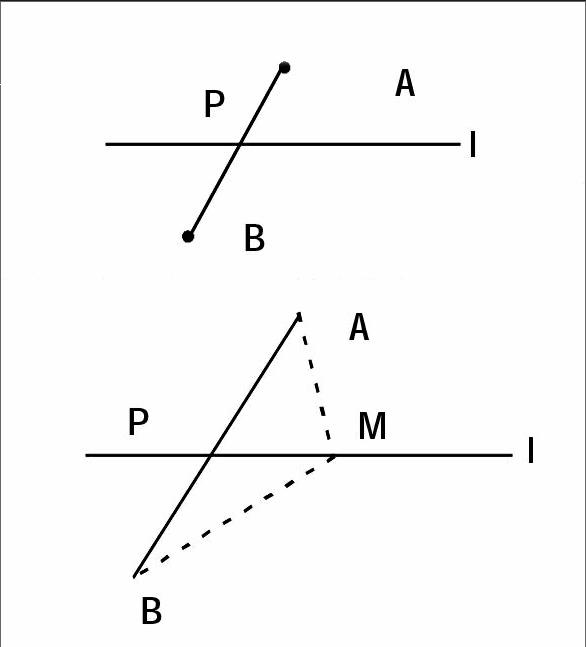
当我提出：“l上P点以外其他的点行不行呢？你们能证明这一点吗？用学过的哪个知识可以解决这个问题？”

我们在l上取P点以外的任意一点M，连接MA、MB。根据三角形任意两边之和大于第三边，我们可以得出：在△MAB中，MA+MB>AB，所以，P点即为所求。

这是一个简单的题目，不仅帮助学生回顾了小学知识，巩固了新学习的知识，而且让学生有了证明的意识。

数学的魅力正在于此，每时每刻，你总是能找到过去的影子，只要你能平时多点留心，多一点思考，多一点总结。数学学习能成为每个人最好的朋友。

编辑 张珍珍