生物组织中肿瘤定位的TR-adjoint法及应用

陈国平，李怡萱

(重庆邮电大学电工理论与新技术实验室，重庆400065)

0 引言

微波致热超声扫描成像技术(microwave-induced thermo-acoustic tomography，MITAT)是生物医学成像中颇有前途的一种技术，也是医学诊断的一个重要工具，它兼有电磁参数高对比度和超声波长高分辨率的优点。MITAT采用调制的微波脉冲照射生物组织［1］，微波脉冲提供高对比度的照射信号，由于肿瘤和背景介质的吸收系数存在差异，因此，由热效应产生的热膨胀使肿瘤组织产生高幅度的超声波［2-4］，从内向外传播直至被组织周围的传感器阵列接收。由此可知肿瘤是作为MITAT的声源，本文对肿瘤组织的定位其实是解决源反演的问题。

目前大多数研究方法是基于模型的反演，通常使用均匀或随机非均匀模型为背景。时间反转镜(time reversal mirror，TRM)方法被证明比后向背影(back projection，BP)方法具有更高的对比度［5］，与BP相比，TRM技术可以有效地克服多径效应，消除复杂环境对信号造成的时延，它对非均匀媒质中的目标具有良好的成像定位能力。信号在非均匀媒质中传播时，时间反转镜可以实现有效能量的相关叠加，提高信噪比，最终达到最佳的空时匹配滤波。若信号传播的环境不变，接收器阵列发射的时反信号在源发射原始信号的位置重新聚焦，并且介质环境越复杂，重聚焦的信号质量越高，因此大大提高了对目标物体的定位精度［6-8］。然而TRM的实质是通过接收信号特性和物理机制以及环境模型来实现对目标的定位要求，但是通常生物组织中密度和声速等参数的分布情况是未知的，MITAT中热声源(肿瘤组织)信息也是未知的，因此，生物组织环境的建模成为肿瘤定位一个重要的前置过程。

较为先进的快速行进方法(fast marching method，FMM)首先假设一个环境分布，根据测量数据得到的渡越时间(time of fly，TOF)和路径计算得到的TOF运用同时代数重建技术(simultaneous algebraic reconstruction technique，SART)对假设的环境分布进行迭代更新，从而重建真实的环境分布［9］。在一定条件下TR-FMM能较好地估测出信道参数的分布，也能解决TRM技术的难点，但是在非均匀的生物组织中使用TR-FMM算法只考虑了几何光学和费马原理，没有考虑衍射方面，并且TR-FMM必须知道天线的起始位置，有时也不能满足复杂生物环境中肿瘤这一类主动源的高精度定位需求。

为了进一步提高MITAT对生物组织中肿瘤定位的精确度，本文提出TR-adjoint方法，将时间反转技术和adjoint理论结合应用在生物组织肿瘤定位的研究中。该方法使用肿瘤作为主动源发射信号，天线获得传播结果，其中包括生物组织的非均匀介质分布信息，然后用adjoint方法提取相关信息，建立并迭代更新合成的声速模型，使合成肿瘤信号与观测肿瘤信号之间的差异最小化，更新后的模型可用于TRM定位肿瘤源。这是一种仅通过观测接收到的信号，就能自适应求解复杂传播环境信道信息的新算法，具有较强的研究价值。

1 TR-adjoint原理及应用

MITAT中影响目标成像的因素有声密度、声速度以及发射源的位置，通常声密度的影响非常小，可以被忽略，本文仅讨论声速度的影响。TR-adjoint方法的主要思想是假设一个介质参数模型，根据此模型在接收器处获得合成信号，因此，我们可以根据真实的和假设的介质参数模型得到观测信号和合成信号之间的差异，这种差异可以通过走时的失配函数来量化，然后根据这个差异用共轭梯度法迭代更新假设的模型参数，直至使观测信号和合成信号之间的差异在一定准则下达到最小，从而获得理想的参数模型，即足够接近真实情况，然后对肿瘤源进行准确定位。

1.1 走时失配函数分析

我们的目的是最小化二乘走时失配函数［10］，即最小化合成数据和真实数据之间的差异，关键是计算出衡量差异大小的失配函数的灵敏度内核。定义走时失配函数为

(1)式中:m表示模型参数，非均匀生物组织的介质参数可以用m(ρ，c)表示，ρ是声密度，c是声速分布;N为接收天线总数;Tr(m)为在假设的模型m下第r根接收天线预测合成信号的走时;Torbs为观测信号的走时。失配函数的梯度为

(2)式中，δTr是走时Tr的Fréchet导数。这里Fréchet导数定义为位函数对空间任意一点介质某个物理量变化的灵敏度函数，根据合成的和观测的波形互相关有如下表达［11-12］，

(3)式中:wr是时间窗函数，取决于模型参数的变化范围，以确保稳定的互相关，比如最高和最低的声波速度可以确定最短和最长的时窗;T表示一个周期，si(xr，t)表示第i个接收天线获得的合成信号;δsi是由模型扰动δm引起的合成波场的变化。Nr是归一化因子，定义为

(4)式并中，δsi是由模型扰动δm引起的合成波场的变化。将δsi的玻恩近似形式［13］代入到(3)式和

(2)式中得:

(5)式中，sj(x'，t')表示si(xr，t)的时间反转传播;si(xr，t)是可以通过接收器观测到的信号。接收器用时反信号作为虚拟发射源，计算观测数据与合成数据时反的差异，即产生adjoint波场。利用格林张量的相互作用Gij(x，x';t－t')=Gji(x'，x;t－t')，定义走时adjoint波场为

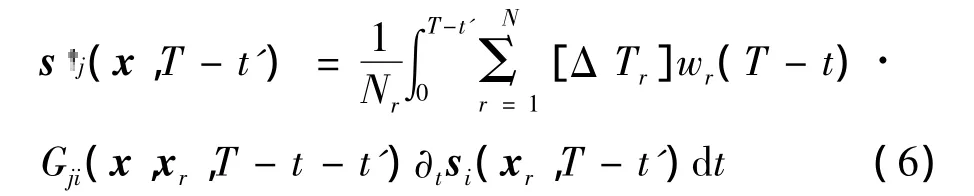
因此，走时的adjoint源定义为

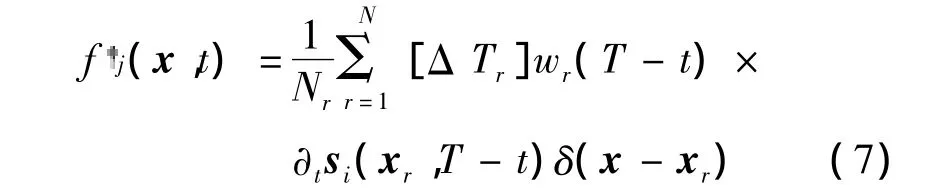
根据下面各向同性的介质模型参数之间的关系［14］:

(8)式中:κ是体积模量;μ是剪切模量，因为MITAT源反演方法通常是在声学近似下进行的，往往假设生物组织的传播介质是各向同性且静止的，产生的压力波是无旋流的，所以，可以忽略剪切模量μ(x)。(8)式中参数 δjk，δlm，δjl，δkm，δjm，δkl具体说明见文献［14］。另外，密度参数被认为是均匀分布的。因此，将(8)式代入到(5)式中，则失配函数的扰动可以简化用体积模量来表示为

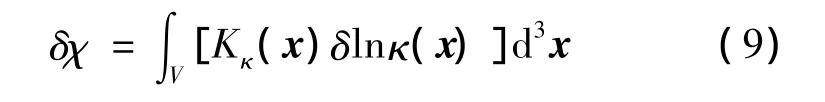
根据TR-adjoint的目的是估计生物组织环境的声速分布，则声速内核Kc用体积模量内核Kκ表示为

在对电力系统变电站运行管理的过程中，应该结合国家的相关要求，与电气企业的发展现状，做好科学合理的规划工作，从而保证电力变电系统的顺利运行。在这个基础上，应该落实各工作人员的工作职责，要求每一个工作人员都需要遵守相关的制度，按时完成工作任务，做好变电运行的保证工作。

(11)式中，s(x，T－t)·s(x，t)实际上是合成波场和伴随波场中每个时间帧互相关的总和，以上理论分析出了声速c(x)与走时失配函数的Fréchet导数的关系，可知由当前模型的波场和adjoint波场之间的相互作用得到参数灵敏度内核，随后，再用共轭梯度法不断迭代更新假设的模型，直到找到最佳的参数模型为止。

1.2 共轭梯度法

本文应用非线性共轭梯度法来迭代参数模型，该方法开始于一个初始的均匀模型m0，上文中提到非均匀生物组织的介质参数可以用m(ρ，c)表示，m0即表示介质参数密度和声速是均匀分布的初始模型，在该初始模型下进行前向模拟产生合成信号。由(1)式计算出初始的失配函数χ0，由(7)式计算出走时的adjoint源，adjoint源在与前向模拟相同的模型中进行时间反转传播，由(11)式计算出失配函数梯度的灵敏度内核Kκ，对不同位置的接收天线得到的初始Kκ进行求和，将此和定义为g0，g0=表示失配函数的初始梯度。并设最初的共轭梯度搜索方向等于负的失配函数初始梯度，即p0=－g0，如果‖p0‖＜ε，其中ε是一个极小的值，那么模型m0则是要求的模型。反之，

①进行线性搜索获得标量vk，使的值最小化，其中:

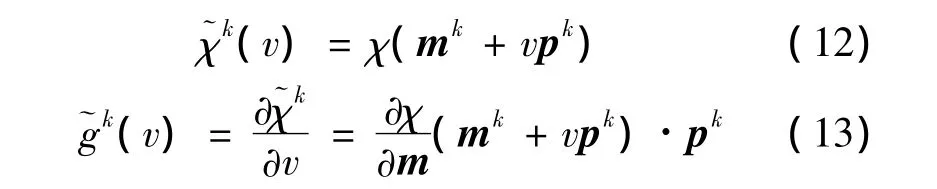
②更新参数模型:mk+1=mk+vkpk，然后计算

③更新共轭梯度的搜索方向p:

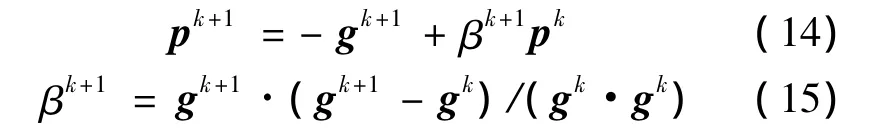
2 TR-adjoint的仿真实例

为了验证我们所述的TR-adjoint方法对生物组织肿瘤定位的有效性，我们进行了如下的仿真实验。在仿真过程中，我们主要考虑生物组织中声速模型估计的准确性及肿瘤定位的精确性。

图1为假设的均匀介质参数模型、主动源和接收器阵列的模拟设置图。仿真区域采用20×20像素的完全匹配层(perfectly matched layer，PML)吸收边界，总像素数为250×250，模拟的生物组织大小为150 mm×150 mm。如图1所示，传播介质密度为1 000 kg/m3，传播介质声速为1 500 m/s。200个接收器均匀地分布在半径为60 mm的阵环上，我们假设主动源(肿瘤组织)位于离中心位置在X轴正方向20个像素，发出的信号强度归一化并且波形是高斯脉冲。

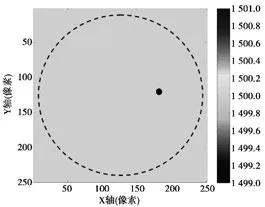
图1 假设参数模型、主动源和接收器阵列设置Fig.1 Supposed model parameters，active source and receiver array

根据初始假设的均匀介质参数模型开始应用本文所提出的TR-adjoint方法，每迭代一次，模型就被更新一次，根据更新的模型经过前向模拟后即更新了合成信号，然后由合成信号重新计算(9)式的声速内核和(7)式的伴随源，直到观测信号和更新后的合成信号之间的走时失配函数达到收敛。真实的介质参数模型、主动源和接收器阵列设置如图2所示。假设的参数模型经过12次迭代后的仿真结果如图3所示。

图2为真实的介质参数模型、主动源和接收器阵列的模拟设置图。仿真区域采用20×20像素的完全匹配层吸收边界，总像素数为250×250，模拟的生物组织的大小为150 mm×150 mm。如图2所示，传播介质密度为1 000 kg/m3，传播介质声速为1 500 m/s，为验证重建的生物组织的声速度分布的有效性，设置2个半径为15 mm，声速为1 650 m/s的高速区分布在均匀介质区域(167，167)，(83，83)处，另外2个半径为15 mm，声速为1 350 m/s的低速区位于仿真区域(83，167)，(167，83)处，200个接收器均匀的分布在半径为60 mm的阵环上。主动源肿瘤组织位于仿真区域的中心位置(125，125)，发出的信号强度归一化并且波形是高斯脉冲。

图2 真实参数模型，主动源和接收器阵列设置Fig.2 Real model parameters，active source and receiver array

图3 假设的参数模型经过12次迭代后的仿真结果Fig.3 Results of supposed model with 12 iterations

图3是经TR-adjoint方法得到的生物组织声速模型，从图3中可以明显看出经过12次迭代，假设的参数模型已经极其接近图2中的真实模型。

图4显示了每次迭代更新后失配函数的大小，失配函数用来衡量真实与合成信号之间差异的大小，因此失配函数的值越小，表明差异越小，当失配函数达到收敛时即差异达到最小，此时假设的模型最接近真实情况，从图4中可以看到，在第4次或第6次迭代后失配函数的大小已经下降了92%，12次迭代后失配函数达到收敛，大小几乎接近于零，可见此时的模型即为所要求的最佳声速模型。最后在此模型下运用TRM技术对肿瘤组织进行定位，结果如图5所示。图2中真实发射源处于仿真区域(125，125)，仿真结果中肿瘤组织位于(124.745 3，124.745 4)，由此可知定位误差为0.255 mm。比在生物组织常规环境的TRM定位技术提高将近60多倍。

图4 迭代次数与失配函数大小关系Fig.4 Relationship between the number of iterations and the size of the misfit function

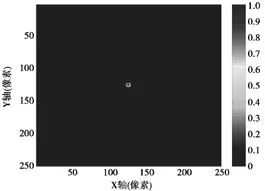
图5 肿瘤组织定位结果Fig.5 Tumor cell localization results

在实现TR-Adjoint算法时，为了避免在仿真运行中存储所有s场与s+场的时间步长，可以通过在特定的一个步长中使用TR方法得到s(x，t)场与s(x，T－t)场的相互作用。在一个时不变的媒质中检测收集信号时，TR方法可以在T－t时间步长时重现波场，这些过程可通过把时反信号作为初始条件来实施。另外，算法需要使用正反向模拟波场，计算量较大，为提高仿真效率，算法使用基于快速傅立叶变换(fast Fourier transform，FFT)的伪谱时域算法(pseudo spectral time domain，PSTD)计算内核以实现波场的精确计算。共轭梯度迭代算法实现简单，内存需求小，在全波形反演中得到广泛应用。

对于定位一个主动发射源的目标物体来讲，在64位的Windows 7系统平台上，利用Matlab 7.1软件，其中计算机的配置为4 GB的内存，双CPU，运用adjoint算法对乳腺组织中的肿瘤定位技术仅仅需要10 min的时间。如果在实验以及仿真中有更加精良的硬件设备，那么定位精度将会更加准确。所有的这些都表明adjoint对生物组织肿瘤这一类主动源定位具有很大的价值。

3 结束语

在介质参数模型未知的MITAT环境中应用TR-adjoint方法，可提高生物组织中肿瘤定位的精度。仿真结果表明，TR-adjoint方法不仅可以较逼真地重建介质参数模型，而且可以对肿瘤进行高精度定位，定位误差仅为0.255 mm，比传统TRM方法有较明显的定位优势。此外，该方法计算波场时采用全波模拟技术，可以满足MITAT对成像的有限频率特性要求。TR-adjoint方法显著的优点是仅通过接收器接收到的信号就可以估计和更新所有的模型参数，进而对肿瘤源进行高精度定位，因此在实际应用中具有相当大的价值及前景。

［1］KELLNBERGER S，HAJIABOLI AR，RAZANSKY D，et al.Near-field thermoacoustic tomography of small animals［J］.Phys.Med Biol，2011，56(11):3433-3444.

［2］LIU L，XU Y，WANG L V.Transcranial Thermo-acoustic Tomography:A Comparison of Two Imaging Algorithms［J］.Medical Imaging，IEEE Transactions on，2013，32(2):289-294.

［3］CHEN GuoPing，ZHAO Zhiqin，GONG Wei，et al.The Development of the Microwave-Induced Thermo-acoustic Tomography Prototype System［J］.Chinese Science Bulletin，2009，52(12):1786-1789.

［4］XIONG W，BAUER D R，WITTE R，et al.Microwave-Induced Thermo-acoustic Imaging Model for Potential Breast Cancer Detection［J］.IEEE Trans Biomed Eng，2012，59(10):2782-2791.

［5］XU M，WANG L V.Pulsed-microwave-induced thermoacoustic tomography:Filtered backprojection in a circular measurement configuration［J］.Medical Physics，2002，29(8):1661.

［6］BAL G，RYZHIK L.Time reversal and refocusing in random environment［J］.SIAM Appl Math，2003(63):1375-1498.

［7］MOSZKOWSKI Ben.Compositional Reasoning using Intervals and Time Reversal［J］.Annals of Mathematics and Artificial Intelligence，2014，7(1):175-250.

［8］XIA Yunlong，FU Yongqing.Refocusing with Time Reversal Mirror in Random Medium［J］.Procedia Engineering，2012，(29):2600-2604.

［9］WANG Jingguo，ZHAO Zhiqin，SONG J，et al.An Iterative Method for Correcting the Acoustic Refraction in Heterogeneous Tissue for Microwave-Induced Thermo-Acoustic Tomography［J］.Progress in electromagnetics research，2012(130):225-240.

［10］周小娟，李春晓.基于偏最小二乘分析和稀疏表示的目标跟踪算法［J］.重庆邮电大学学报:自然科学版，2014，(1):104-110.

ZHOU Xiaojuan，LI Chunxiao.A partial least squares analysis and sparse representation of the target tracking algorithm based on［J］.Journal of Chongqing University of Posts and Telecommunications:Natural Science Edition，2014，(1):104-110.

［11］MARQUERING H，DAHLEN F，NOLET G.Three-dimensional sensitivity kernels for finite-frequency traveltimes:the banana-doughnut paradox［J］.Geophysical Journal International，1999，137(3):805-815.

［12］DAHLEN F，HUNG S H，NOLET G.Fréchet kernels for finite frequency traveltimes—I.Theory［J］.Geophysical Journal International，2000，141(1):157-174.

［13］HUDSON J A，HERITAGE J R.The use of the Born approximation in seismic scattering problems［J］.Geophysical Journal of the Royal Astronomical Society，1981，66(1):221-240.

［14］FICHTNER A，BUNGE H P，IGEL H.The adjoint method in seismology:I.Theory［J］.Physics of the Earth and Planetary Interiors，2006，157(1):86-104.