一种3D 空间中的两级力导引可视化算法
2015-12-15雷大江
吴 渝,林 茂,雷大江
(重庆邮电大学网络智能研究所,重庆400065)
0 引言
复杂网络可视化是当前的热门研究领域,通过可视化能够挖掘传统方法无法直观得到的内部结构信息,增加对复杂网络的理解程度。当前,主要的可视化方法是Edges[1]提出的力导引布局算法,其基本思想是将整个网络看成一个弹簧受力系统,系统中受到的弹力总和为系统的总能量。系统中每个顶点在弹力作用下不断调整位置减小受到的弹力,直到系统总能量减少到最小值时停止。
在传统的2D平面上,Kamada[2]提出的KK算法使弹力模型遵循“胡克定律”,其可视化结果美观度得到了很大提高;Fruchterman[3]在弹力模型中增加了布局空间大小的限制因素,使可视化布局适应于布局平面大小的变化;黄竞伟等[4]通过采用遗传算法减少了迭代次数,降低了可视化布局的时间复杂度;黄茂林[5]通过多层次聚类的方法使可视化适用大型网络。还有很多其他算法[6-7]改进了布局方式使力导引方法适用于不同网络类型,并使可视化结果更加方便用户获取网络中的隐藏信息。
但是,Ware[8]指出2D平面相对于3D空间其布局空间较小、深度值不够从而体现不出立体感,并使可视化结果缺乏交互性。因此,一些3D可视化算法被提出来。Bruβ[9]通过分析3D空间特征,改进了能量迭代的方法,大大降低了时间复杂度;Harel[10]在3D空间中采用多尺度布局,即每次只显示源网络的部分骨架网络,提高了网络的布局时间效率;Gajer[11-12]通过预布局的方式能够快速地在3D空间中得到最终布局;Ahmed[13]分析了复杂网络的幂律特性,并通过节点度大小对网络进行聚类,然后采用较成熟的2D可视化方法把每一个聚类分层次的布局在3D空间中,其可视化布局能够直观分辨出重要节点,且具有较好美观性;吴鹏[14]在3D中对社会网络采用多层次布局方式,其可视化结果能够显示社会网络中的子群分布。
综上所述,目前2D可视化已经较为成熟。而由于3D可视化具有更好的交互性,提供了更加生动的可视化展示,3D可视化算法逐渐成为可视化研究热点。然而,目前的3D可视化算法都是采用优化迭代算法、预布局、多尺度布局、多层次布局等方式优化布局方式,减小时间复杂度,可视化过程中缺乏复杂网络特征分析,因此不能可视化复杂网络的真实结构,比如社团结构。同时,在国内可视化研究也相对较少[15],特别是3D可视化。
本文引入复杂网络结构特征分析方法,基于Kamada提出的KK算法[2],提出了两级KK 3D力导引算法(two-tier KK,TTKK)。算法改进了2D KK算法,使算法适应于3D空间布局,并首先对源网络进行聚类分析,建立抽象网络。然后,在3D空间中分2级依次对源网络的抽象网络和子网络进行KK布局。其最终可视化布局结果能够较完整地展示复杂网络结构特征。
1 KK力导引算法基本原理
Edges提出的力导引算法主要分为2部分:建立能量计算模型,即弹力模型;以及迭代减小系统总能量。在能量计算模型上,KK算法遵循“胡克定律”
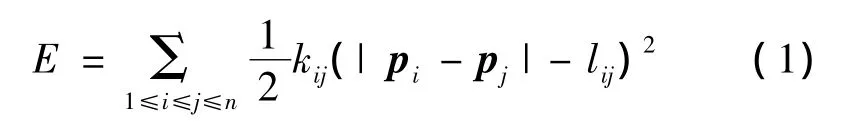
同时,算法首次提出了“理想距离”的概念。2个顶点间的理想距离与2个顶点的最短距离成正比

(1),(2)式中:pi是顶点vi对应的位置向量;n为顶点数;kij是顶点vi和vj之间的弹力系数;lij是顶点vi和vj之间的理想距离,它由vi和vj的最短距离dij以及布局宽度L0共同决定。
在减小系统能量的方法上,如(3)式所示,KK算法通过求解每一个顶点对E的偏微分方程来不断减小系统总能量。在计算过程中,KK算法为方便计算,假定顶点pm(xm,ym)是当前Δm值最大的顶点,且在移动pm时其他顶点都相对固定。则pm的位移向量(δx,δy)可以通过(4),(5)式求解,使pm移动到(xm+δx,ym+δy)处,更新pm的位置。
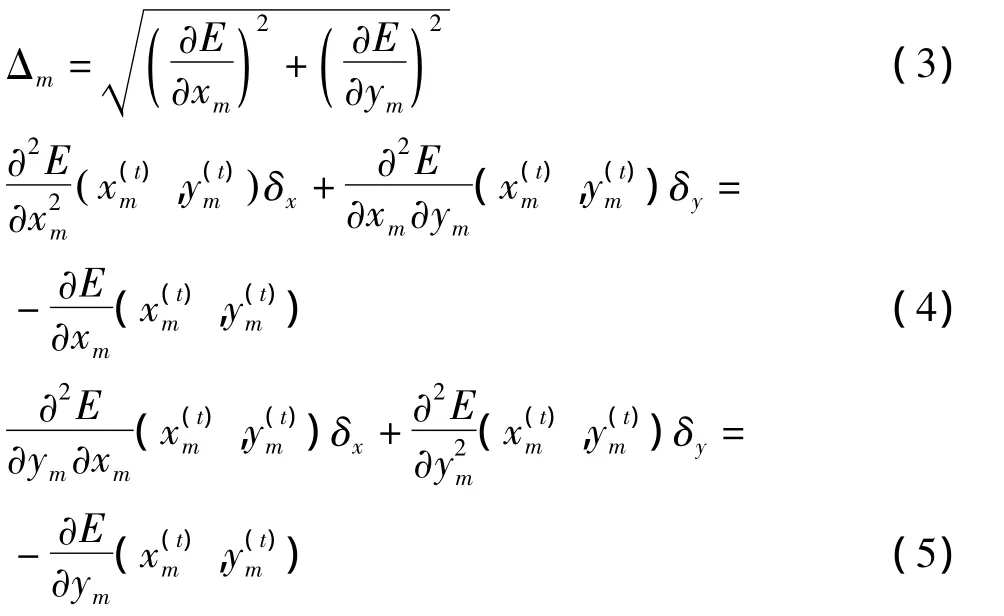
(4)-(5)式中,(x(mt),y(mt))是点pm在第t次迭代后的位置。然后,反复迭代减小系统中能量,直到每一个顶点的Δ值都足够小并满足要求时停止,得到最终布局。
2 两级KK力导引布局算法
2.1 问题提出和算法基本思路
KK 算法能量模型遵循“胡克定律”,最终的布局结果具有良好的对称性[16],在2D平面可视化中得到广泛应用。但是,KK算法在能量减小过程中迭代次数较多,时间效率低。本文在2D平面KK算法的基础上,把KK算法应用到3D空间中,并通过实验分析改进了KK算法的时间效率。
另一方面,目前,3D算法主要集中在如何改进算法的时间效率上,且这些可视化算法都是直接对复杂网络中节点间的相互连接关系进行分析,从而进一步布局得到可视化结果。算法布局较缺乏对复杂网络的内部特征的分析,布局结果破坏了复杂网络的社团、节点重要度等结构特征。
如图1所示,本文借用复杂网络中社区划分的思想,采用能够较完整地保持网络原始物理结构的edge betweenness[17]算法对网络进行聚类分析,使每个聚类的顶点在100以内[11],并通过分析聚类之间的链接关系构建抽象网络。得到抽象网络后,TTKK算法分2级分别对网络布局:第1级抽象网络布局和第2级聚类子网布局,TTKK算法流程如图1所示。在抽象网络布局上,算法提取子网络的特征向量重新定义“理想距离”,使KK算法适应抽象网络特性;使用3DKK算法对抽象网络布局得到每个子网络的布局中心点,每个子网络在布局中心点处随机初始化顶点位置,然后使用3DKK算法进行布局。
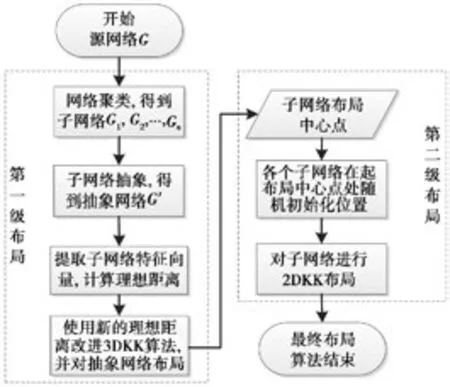
图1 TTKK算法流程图Fig.1 Algorithm flow chart of TTKK
2.2 3D空间中的KK力导引算法
在3D空间中,KK算法的能量同样可以使用(1)式计算得到。但是在迭代减小系统能量时,网络中每个顶点的能量Δm的计算方法需要加入对深度坐标轴z的影响因子
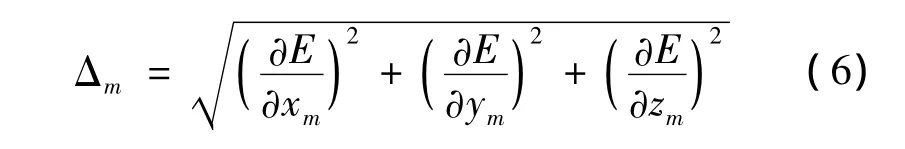
同理,求解顶点pm每次迭代后的位移向量(δx,δy,δz)的方程也有所改变,如(7)-(10)式所示。
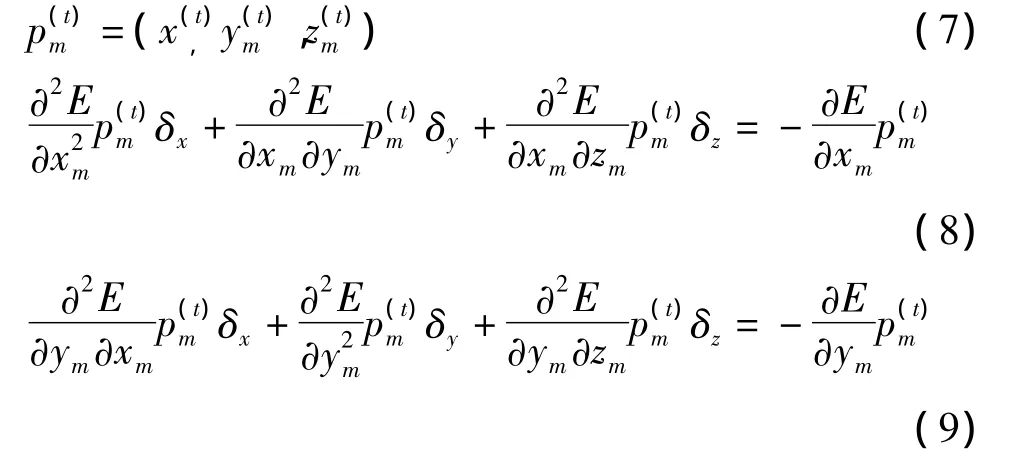
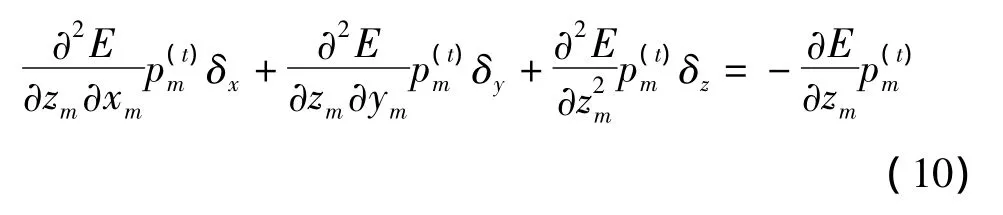
另一方面,KK算法在减小能量过程中迭代次数太多,使网络布局难以在短时间内完成。实验发现KK算法在迭代过程中能量的减小将逐渐减缓。假设布局网络的定点数为n,则在前n次迭代过程中能量减小最快,布局中顶点位置变化最强烈;到第4n次迭代时虽然能量也在减小,但是布局中的顶点变化较小,这时的布局已近基本稳定,接近最终布局;在4n次迭代之后,虽然布局的美观性逐渐增加,但是顶点位置的改变微弱。
表1展示了使用仿真数据K15完全图和日本空手道Zachary[18]俱乐部的公开数据进行KK算法布局试验的结果。其中t为算法迭代的时间,n是网络中的顶点数,t=n代表迭代n次后所花费的时间,以此类推。从表1中可以看出不论是真实数据Zachary,还是仿真数据K15,由于初始布局顶点是随机分布,布局十分混乱;当迭代n次后最终布局的骨架基本显现出来,可以很明的看出这个过程布局变化激烈。从第3n次布局开始,每次迭代后的虽然布局对称性、美观度逐渐增加,但是网络中各个点的位置变化却十分微弱。因此,本文在网络布局中限制了KK算法能量减小过程的最大迭代次数。根据实验,本文在速度和美观度上进行折中选择,取4n为最大迭代次数。
设源网络为G=(V,E),其中V是待布局网络的顶点集,E是待布局网络的边集。则3D空间中改进后KK布局算法可以描述如下。

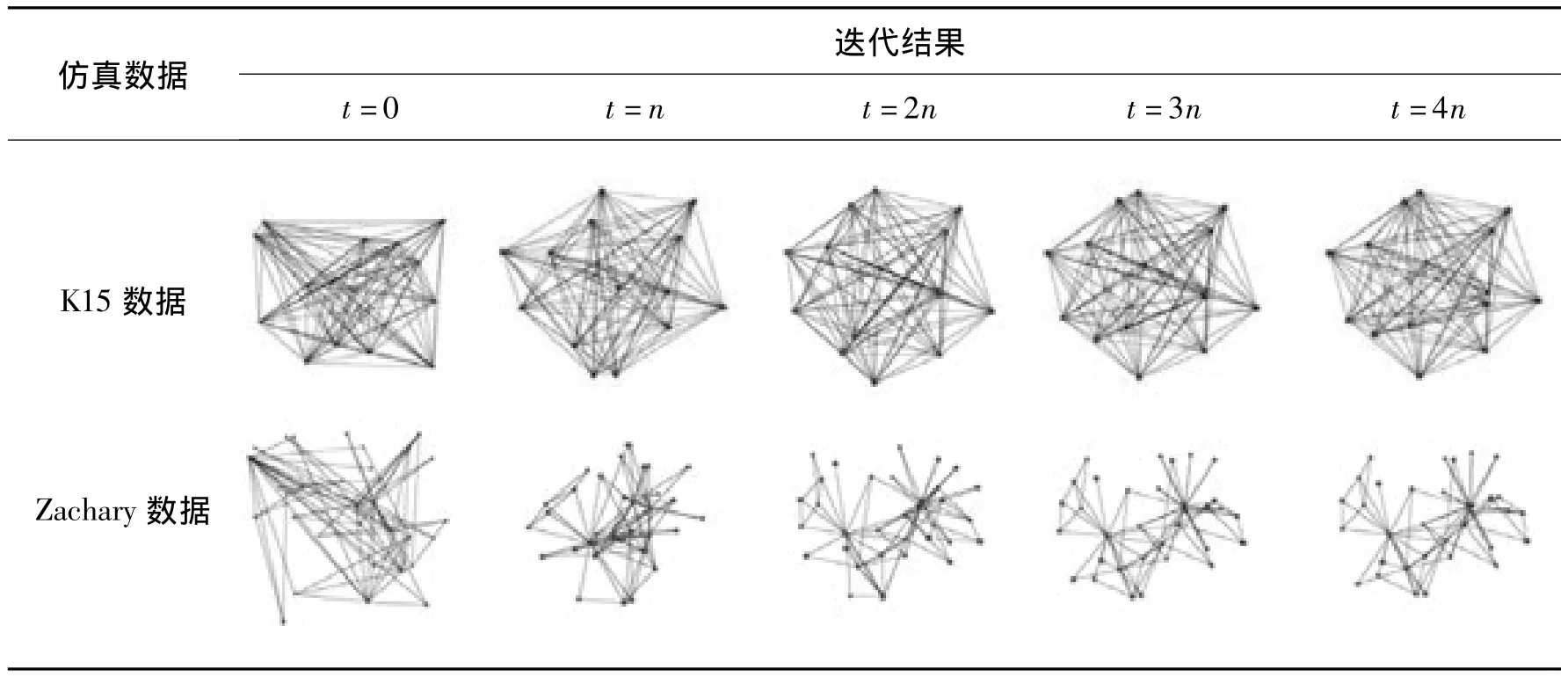
表1 3D KK算法迭代过程布局变化情况Tab.1 Iteration changing situation of 3D KK algorithm
2.3 抽象网络特征向量构造方法
在TTKK算法中使用Edge Betweenness算法对网络G进行聚类得到子网络G1,G2,…,Gn,并建立抽象网络。抽象网络中的一个顶点代表一个子网络,同时如果2个子网络中的任意2个顶点在原网络存在连接则在网络G'中2个子网络对应的顶点间存在一条边。建立网络后进一步使用KK算法对抽象网络布局。
但是,由于抽象网络中的每1个顶点代表1个子网络,而网络本身具有的特性与原始的顶点具有不同的属性,不适合以最短距离来定义聚类间的理想距离。因此,本文通过子网络中每个顶点在源网络G中的聚类系数[19]值的和、Page Rank[20]值的和构建子网络的特征向量T,如(11)式所示,然后计算2个子网络之间的余弦相似度来得到2个聚类间的理想距离
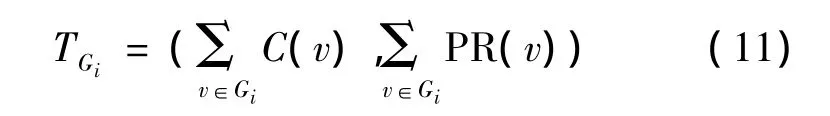
(11)式中,C(v)指聚集系数值,它表明网络中节点的聚集性,也就是说同1个节点的2个相邻节点仍然是相邻节点的概率有多大,反映了网络的局部特性。计算公式为

(12)式中:kv代表与网络中点v连接的节点数量,即邻居数;Ev表示这kv个邻居之间的实际存在的边数。
PR(v)指Page Rank值,即节点的影响力值,它反映了节点在网络中的重要程度。
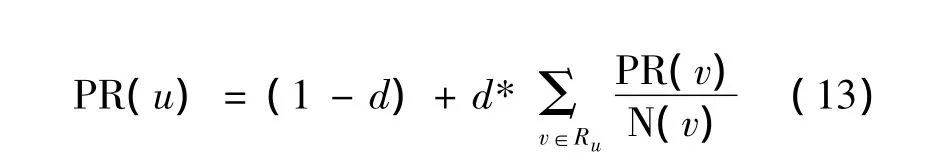
(13)式中:PR(u)是节点u的PageRank值;PR(v)是节点v的PageRank值;Ru是链接到节点u的节点集合;N(v)为节点v向外的所有链接数;d是与节点u属性相关的随机概率,一般情况下d=0.85。
2.4 抽象网络布局及子网络布局
通过计算每个2个子网络特征向量的余弦相似度得到抽象网络G'中相互2个顶点的理想距离l'ij,计算公式为
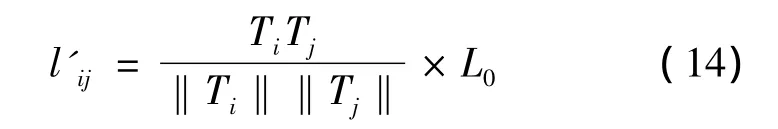
(14)式中,L0是可视化布局的宽度,本文取L0的取值为3D布局空间的直径。新的“理想距离”定义l'ij加入了复杂网络特征因素,KK算法使用l'ij进行布局即可得到每一个子网络的布局中心点,其布局结果能够反映出各个子网络在源网络中的相互关系。然后,在子网络布局中心点处对子网络进行KK布局,得到最终的可视化布局。
3 实验及结果分析
为对比TTKK算法可视化布局效果,本文分别选取3DKK算法和Ahmed提出的算法进行对比。其中,3DKK算法遵循胡克定律,是基于2DKK[2]算法在3D空间中的应用,TTKK算法的每一级布局都是基于3DKK算法布局算法的;Ahmed[13]算法基于连接度的聚类把网络分为3层,并把每一层节点分层次地布局在3D空间中,每一层上的节点都采用较成熟的2D布局算法进行布局,整个算法思想与TTKK算法类似。因此,文本分别将2种算法作为对比对象,用真实数据进行可视化布局,以评估本文算法。
3.1 实验数据
本文使用3组公开数据集进行实验。其中Dolphins数据是一个由Lusseau[21]通过7年的研究,并记录下海豚社交网络数据集,Ca-AstroPh(Astro Physics collaboration network)通过Arxiv在线出版并投稿到Astro的Physics类的科研合作网络,Smyth是关于Padhraic Smyth[22]的出版物网络,表2展示了各组实验数据的详细信息。
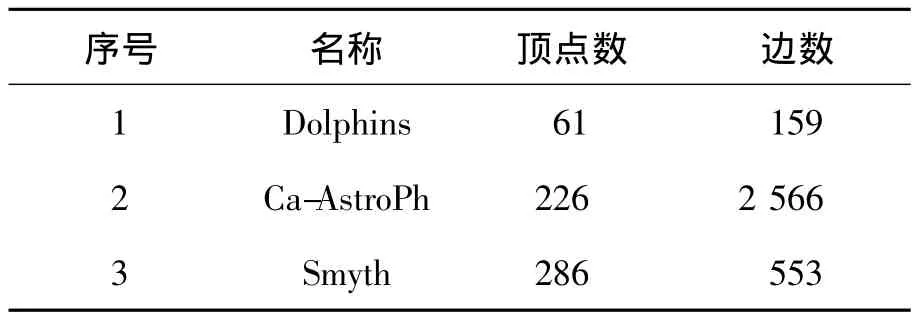
表2 实验数据集Tab.2 Dataset in experiments
3.2 可视化结果分析
采用3.1节中的数据集,本文分别对KK算法、TTKK算法和Ahmed提出算法进行了实验。图2是Dolphins数据集可视化对比情况,其中图2a是TTKK算法的初始布局,图2b是TTKK算法可视化结果,图2c是Ahmed算法可视化结果。图3是TTKK算法采用Ca-AstroPh数据集进行实验的结果,图3a和图3b是分别从不同角度下观看的结果。图4是Smyth数据集可视化对比情况,图4a是TTKK算法可视化结果,图4b是TTKK算法可视化布局旋转后的视图,图4c是Ahmed算法可视化布局结果。
从图2a和图2b中可见TTKK算法从初始的随机布局得到对称性较好的可视化布局。同时,可以看到在可视化结果中清晰地显现出3个聚类类结构,表明Dolphins数据集中具有3个关系网络。在图2c中由于Ahmed算法通过节点度大小来直接进行聚类划分,而Dolphins数据集中不存在度大于15的节点,从而造成可视化结果只有2层。而且图2c相对于图2b,其可视化结果并不能很好地反应出网络的真实形态,可视化结果本身的美观效果也不够理想。同样的,KK算法在Ca-AstroPh(图3)和Smyth(图4a和图4c)数据集下的可视化结果中也能够清楚完整地展示网络的结构特征,而且能够凸显出网络中的各个重要节点。
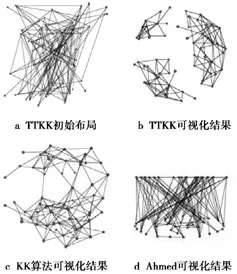
图2 Dolphins数据集可视化结果对比Fig.2 Visualization results comparison of dolphins
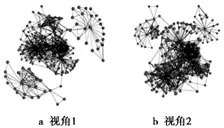
图3 CA-AstroPh数据集可视化结果Fig.3 Visualization results of CA-AstroPh
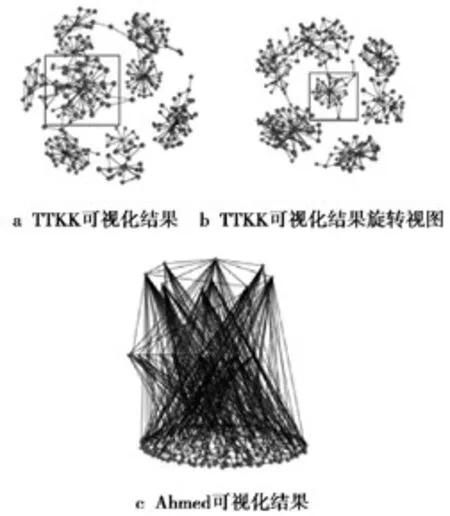
图4 Smyth数据集结果对比Fig.4 Visualization results comparison of Smyth
另一方面,在图4a的可视化结果中左边有一个子网络的布局产生了较严重的点遮挡情况,但是,TTKK算法可视化结果可以通过在3D空间中进行旋转得到图4b,从图4b的角度就能够清晰地看到这部分子网络的结构。而在Ahmed的可视化布局结果中虽然美观度在这个数据集中有很大的提高,但是结构上只得到顶层节点具有较高重要度,而且最底层的节点之间的关系混乱。不论在哪一个角度观看都不能得到较满意的结构信息。
综上,TTKK算法在3D空间下能够十分完整地展现复杂网络的聚类结构特征。
3.3 算法效率分析及实验对比
TTKK的运行时间主要受2个方面影响:聚类算法运行时间以及能量迭代运行时间。其中Edge Betweenness算法的时间复杂度为O(m2n),m为边数,n为顶点数。同时,假设KK算法的时间复杂度为O(KK),则TTKK算法可以在O(m2n)+k*O(KK)的时间复杂度中完成布局,其中k为一个常数因子。而且由于限制了最大迭代次数,KK算法的迭代时间大大减小。同理,若Ahmed每一层的布局都采用KK算法,则Ahmed的算法时间复杂度为O(n)+k*O(KK)。但是,由于复杂网络存在幂律定律,即节点度数较大的顶点较少,Ahmed算法的聚类方式大部分都会分布在最底层中,如图3c所示。因此,Ahmed的时间复杂度中的常数因子k较大,而且随着网络的增大Ahmed的增长越快。
本文采用Java语言分别实现了KK,Ahmed,TTKK 3个算法,并在Windows7(CPU为i3 2.1 GHz)平台上分别对KK算法、Ahmed算法、TTKK算法使用表2的数据集进行了3次实验采集算法时间消耗,对3次实验的时间消耗的平均值作为其最终的时间消耗,如表3所示。可以看出Ahmed在网络较小时时间效率较高,而随着网络的增大时间消耗剧增;TTKK算法虽然在小型网络中复杂度较高,但却不会随着网络的增大而剧烈变化。最终实验结果与理论分析一致。
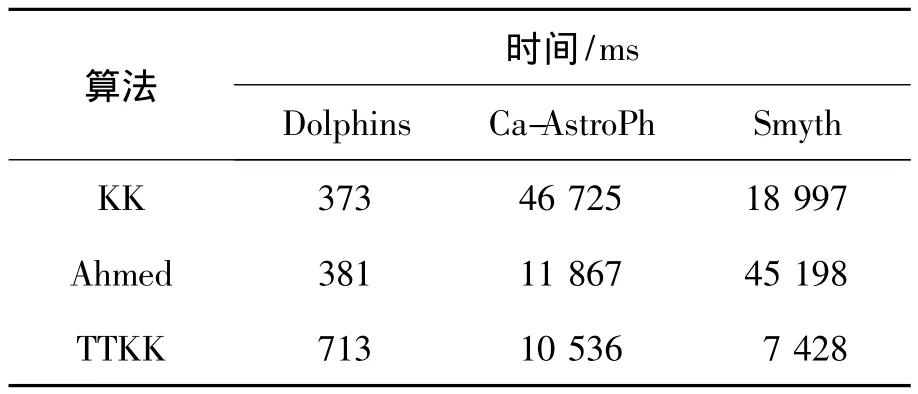
表3 算法时间对比Tab.3 Comparison of algorithm efficiency
4 结论
本文在当前广泛使用的2D平面上的KK力导引可视化算法基础上,结合复杂网络特征,提出了适用于复杂网络的TTKK 3D可视化算法。算法首先通过聚类得到源网络的多个子网络,并构建抽象网络。然后,分2级分别使用3DKK算法对抽象网络和子网络进行布局。TTKK算法解决了可视化结果中不能反映复杂网络特征的问题,能够清晰的展示复杂网络的社团、节点重要度等结构特征。同时,通过改进KK算法的迭代方式可减少算法时间消耗。
但是,目前算法最初的可视化布局不能自动调整视角使布局结果具有最佳的效果,而需要手动调整视角。在下一步工作中,主要对算法布局结果的评定指标进行研究,比如说对称性、信息可见度、结构可视化程度等的定量评定指标的研究,使TTKK算法通过指标值自动调整可视化布局结果的视角。
[1]EADES P.A heuristic for graph drawing.Congressus Nutnerantiunt,1984,42:149-160.
[2]KAMADA T,KAWAI S.An algorithm for drawing general undirected graphs[J].Information Processing Letters,1989,31(1):7-15.
[3]FRUCHTERMAN T M J,REINGOLD E M.Graph drawing by force directed placement[J].Software:Practice and Experience,1991,21(11):1129-1164.
[4]黄竞伟,康立山,陈毓屏.一个新的无向图画图算法[J].软件学报,2000,11(1):138-142.
HHUANG J W,KANG L S,CHEN Y P.A new graph drawing algorithm for undirected graphs[J].Journal of Software,2000,11(1):138-142.
[5]黄茂林,NGUYEN Q V.用多层次聚类法完成的大规模关系图的可视化[J].软件学报,2008,19(8):1933.
HHUANG M L,NGUYEN Q V.Large graph visualization by hierarchical clustering[J].Journal of Software,2008,19(8):1933.
[6]CHAN D S M,CHUA K S,LECKIE C,et al.Visualization of power-law network topologies[C]//,2003 IEEE 11th International Conference on Networks.Sydney:IEEE Press,2003:69-74.
[7]HOLTEN D,ISENBERG P,VAN WIJK J J,et al.An extended evaluation of the readability of tapered,animated,and textured directed-edge representations in nodelink graphs[C]//2011 IEEE Pacific Visualization Sym-posium.Hong Kong:IEEE Press,2011:195-202.
[8]WARE C.Designing with a 2 1/2d attitude[J].Information Design Journal,2001,10(3):171–182.
[9]BRUB I,FRICK A.Fast interactive 3-D graph visualization[C]//Lecture Notes in Computer Science,Graph Drawing.Berlin Heidelberg:Springer,1996,99-110.
[10]HAREL D,KOREN Y.A fast multi-scale method for drawing large graphs[C]//Lecture Notes in Computer Science,Graph Drawing.Berlin Heidelberg:Springer 2001,183-196.
[11]GAJER P,GOODRICH M T,KOBOUROV S G.A multi-dimensional approach to force-directed layouts of large graphs[C]//Lecture Notes in-Computer Science,Graph Drawing.Berlin Heidelberg:Springer 2001,211-221.
[12]GAJER P,KOBOUROV S G.Grip:graph drawing with intelligent placement[C]//Lecture Notes in Computer Science,Graph Drawing.Berlin Heidelberg:Springer 2001,222-228.
[13]AHMED A,DYWER T,HONG S H,et al.Visualization and analysis of large and complex scale-free networks[C]//Proceedings of the 7th Joint Eurographics/IEEE VGTC conference on Visualization.Switzerland:Eurographics Association Press,2005:239-246.
[14]吴鹏,李思昆.适于社会网络结构分析与可视化的布局算法[J].软件学报,2011,22(10):2467-2475.
WU P,LI S K.Layout algorithm suitable for structural analysis and visualization of social network[J].Journal of Software,2011,22(10):2467-2475.
[15]王柏,吴巍,徐超群,等.复杂网络可视化研究综述[J].计算机科学,2007,34(4):17-23.
WANG B,WU W,XU C Q,et al.A survey on visualization of complex network[J].Computer Science,2007,34(4):17-23.
[16]BATTISTA G D,EADES P,TAMASSIA R,et al.Algorithms for drawing graphs:an annotated bibliography[J].Computational Geometry,1994,4(5):235-282.
[17]NEWMAN M E J,GIRVAN M.Finding and evaluating community structure in networks[J].Physical Review E,2004,69(2):026113.
[18]ZACHARY W.An information flow model for conflict and fission in small groups[J].Journal of Anthropological Research,1977,33(4):452-473.
[19]汪小帆,李翔,陈关荣.复杂网络理论及其应用[M].北京:清华大学出版社,2006.
WANG X F,LI X,CHEN G R.Complex network theories and applications[M].Beijing,China:Tsinghua U-niversity Press,2006.
[20]BRIN S,PAGE L.The anatomy of a large-scale hypertextual web search engine[J].Computer Networks and ISDN Systems,1998,30(1):107-117.
[21]LUSSEAU D.The emergent properties of a dolphin social network[J].Proceedings of the Royal Society of London,Series B:Biological Sciences,2003,270(2):186-188.
[22]WU A Y,GARLAND M,HAN J.Mining scale-free networks using geodesic clustering[C]//Proceedings of the 10th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.Texas:ACM,2004:719-724.
