基于粒子群优化与模糊聚类的社区发现算法

孙延维，彭智明，李健波

(1.湖北第二师范学院基础教育信息技术服务湖北省协同创新中心，湖北武汉430205;2.首都信息发展股份有限公司重庆分公司，重庆400014;3.重庆市教育考试院信息处，重庆401147)

0 引言

社交网络(social network)是真实世界里人际交往关系的一个缩影，仍然具有社区结构这一普遍特性。发现社交网络中的社区对探索人际关系模式有巨大的现实意义，而用什么样的算法来挖掘社交网络中的社区则是关键。

经过科研人员的多年努力，社区发现算法的研究已经获得了重大进展。目前，出现了基于稠密子图的社区划分算法［1］，其时间复杂度较低，能适用于大规模网络社区发现，但只能挖掘联系非常紧密的小社区;最小分割聚类算法［2］运行效率较高，但不具备动态识别网络社区总数能力;基于快速展开的社区划分方法［3］具有高效的运行速度，但在某些具有层次性特点的网络中，不能发现网络的社区结构;基于拓扑势的社区发现方法［4］无须指定社区个数，但该算法划分的社区结果受拓扑势的影响;文献［5］中提出的一种改进的GN(Girvan-Newman)算法解决了GN算法计算效率差的问题，但社区划分的准确性较低。

在研究中发现，实际社交网络节点的社区归属具有不明确性，如此会使社区的划分结果不精准，与具体网络的社区结构相距较远。针对此问题，文献［6］提出了改进的K-means模糊聚类的社区发现算法(k-meas algorithm for community structures detection based on fuzzy clustering，NKFCM))，且实验结果说明该算法效果良好，但执行效率较差。因此，本文提出改进的基于粒子群优化与模糊聚类的社区发现算法(community detection algorithm based on particle swarm optimization and fuzzy clustering，PFCM)，该方法运用以云模型为执行条件的粒子群算法自适应地决定最优社区数与最佳社区核心，且能改善NKFCM运行时间代价较大的问题。

1 基于改进的K-means模糊聚类的社区发现算法(NKFCM)

NKFCM［6］包含了有序的算法流程，其描述如下:

1)对社区核心节点进行优化，确定最佳社区个数。首先设定被发现的社区个数为k，有k个最佳聚类核心在k=［2，kmax］中被计算出来，一般取为网络中的节点个数;

2)依照最优的核心节点，将网络在拥有k个社团时的聚类目标值计算出来，当得到最大的聚类目标值时，网络含有的社区数目就被获得，再将社团个数与优化的聚类核心进行输出;

3)利用模糊聚类算法(fuzzy c-meas algorithm，FCM)［6］划分网络社区，得到网络的社区结构。

2 基于粒子群优化与模糊聚类的社区发现算法(PFCM)

2.1 粒子群算法原理介绍

粒子群优化算法(particle swarm optimizer，PSO)［7-8］是一种演化的计算技术(evolutionary computation)，由Eberhart和Kennedy于1995年共同提出的，它源于对鸟群的行为研究演化而来［7］。粒子群算法是一种群体智能方法，其思想的初始来源是模仿鸟群活动，即把任意个体看作一个无体积和质量的轻质粒子。任何粒子都有各自的移动速度，可是每个粒子的移动速度却受到其他粒子与自身移动历史的影响，最优解则通过个体之间共享信息与相互协作来寻找。假设存在一个s维的搜寻空间，空间中存在z个粒子，每个粒子目前所在的位置为psi=(psi1，psi2，…，pis)，且过去所在的最好位置为phi=(phi1，phi2，…，phis)，粒子群以前的最佳位置为pci=(pci1，pci2，…，pcis)。任何一个粒子目前移动的速度为qi=(qi1，qi2，…，qis)。算法首先初始化随机选定的z个粒子，再迭代，在每一次迭代中，每个粒子的位置与速度［9］会按某种准则来更新。第k次迭代更新粒子位置与速度的准则分别为

(1)—(2)式中:w1，w2为加速系数，分别表示调整全局最优粒子与个体最优粒子按自己的方向移动的最大步长;θ为惯性因子;ram为一个在［0，1］的随机数。(1)式等号右边由3个部分构成。粒子维持本身惯性的能力是第1部分，当θ越大，粒子原来速度的权重值被接受的概率也越大;第2部分，即粒子的“认知”部分，表示粒子所通过的“学习”，也是粒子的认知能力;粒子之间有相互学习的能力，由第3部分表示，同时也象征了粒子间互相影响的“社会”作用［10］。

2.2 云模型介绍

本文采用云模型［11-12］作为粒子群算法执行的前提条件。云模型是一个数学模型，用语言值描述了某个概念B与其定量表示之间的不确定转换关系。设I为一个包含精确值的论域，B是I上对应的一个定性概念，对于I上的任意一个定量值v，∀v，v∈I，都存在一个随机数L=τB(v)，且L具有平稳趋势，也表示I在v上的确定水平，v在I上的分布就被定义为云模型，简称云［12］。云的数字特征有期望［11］Ev、熵［12］Em、超熵［12］Hε，即B整体上的定量特征由这3个参数表征出来。

期望Ev:最能代表B的点，且这些点都属于某个数域空间。

熵Em:B的不确定性由Em展现出来，且存在3个方面能够体现此种不确定性。①随机性与模糊性的关联关系被Em显示;②Em表明了B在数域空间内能够承受的云滴［12］群大小;③Em还能表示B的粒度。一般，Em的值越小，云滴的钟形开口［10］展开也越小，概念更微观，随机性、模糊性更小，进行明确的量化也更加容易。

超熵Hε:即Em的熵，当Hε越小，云滴的散布越小，云越稀薄。

粒子在查找最优值的历程中受惯性权重θ的影响，且θ需要自适应调节，θ的值越小，粒子在大范畴内进行搜寻最优越不利，在粒子接近最好值时，其速度则被要求减慢，直到静止在最好值周边。如此，粒子的“早熟”现象就可以被避免。利用在v前提下的云发生器［13］可以获得每个粒子接受θ的概率φi(t)，φi(t)的值越大，粒子搜索最佳值的效率越高。

则

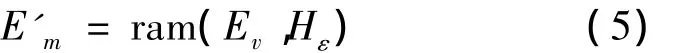
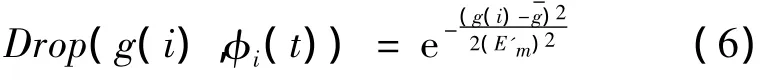
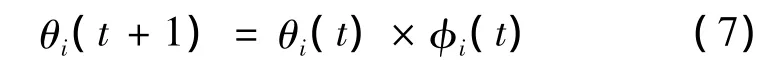
2.3 粒子群优化与模糊聚类的社区发现算法(NFCM)

2.3.1 聚类核心初始化

设V={v1，v2，…，vm}包含m个节点，vm∈Rs表示一个节点，现在计算任意节点vi与vj之间的最短路径D(vi，vj)

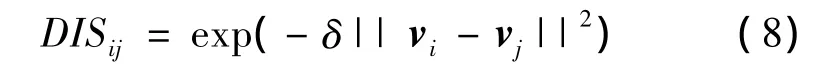
(8)式中:i=1，2，…，hmax，其中，hmax表示最佳社团数;j=1，2，…，m;δ是一个能被调节控制的常数。(8)式反映了节点vi与节点vj在距离上的关系，当DISij的值越大，vi与vj间相隔的距离就越远。

设定任意节点vi的关系度值计算函数为

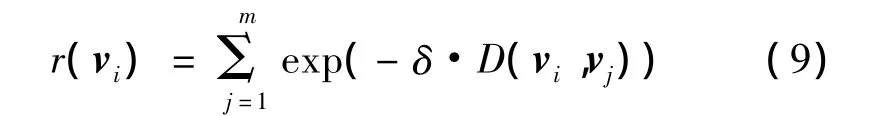
(9)式中:δ是常数，表明了距离关系可以改变;vi与网络中全部节点之间的距离之和确定了r(vi)值的大小，且r(vi)反映了vi周边节点密集的程度。把网络中全部节点的关系度值计算出来，并记为rk(vi)(j=1，2，…，hmax)。设表示网络中第k个聚类核心的关系度值，则确定的函数为

设ξ是个可以变更的常数，且ξ≥0，若DISij≥ξ，就称DISij是vj对于vi的有效半径。对任何节点vi，当网络中存在N个使DISij≥ξ的节点，则决定网络聚类核心的公式为

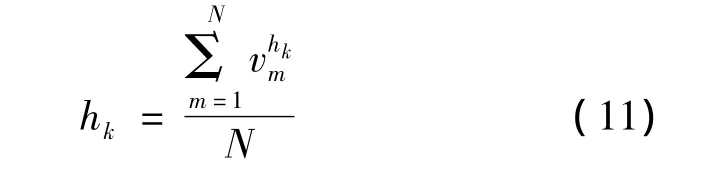
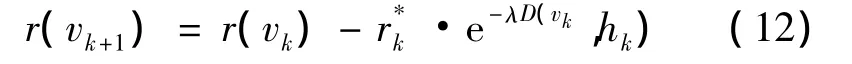
(12)式中:样本里的最大r(vi)值用表示，其值由(9)式计算;λ是常数。

选取聚类核心的流程为(10)—(12)式，迭代此过程m次，就能选择出m+1个聚类核心。终止迭代应满足(13)式。

2.3.2 粒子的编码与适应度函数

1)粒子的编码［10］方式。粒子种群的起始个体由已被优化了的聚类核心组成。设与网络节点相关的信息维数为s，则对粒子进行编码的方式为

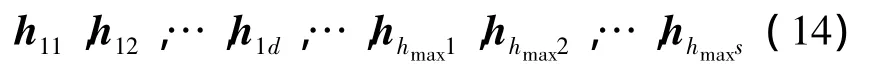
(14)式中，hij(i=1，2，…，hmax，j=1，2，…，s)代表第i个聚类核心的第j维编码。如此每个粒子的信息就转化为一个hmax×s维的数据。

2)适应度函数［10］。FCM算法获得最小值的方法为迭代优化目标函数值，且适应度函数的定义为

(15)式的函数值越小，表示划分的聚类效果较差，聚类核心选取有较大的偏差，聚类质量则不高。

2.3.3 算法的基本流程

1)网络中每个节点的关系度值都由(9)式计算，则首个被预先挑出的聚类核心即为具有最大关系度值的节点h1，并计算h1的有效距离，确定h1的有效辐射点和数量，再依照(11)式更新网络聚类核心;

2)更新后样本的关系度值都依据(12)式计算，选出新的核心，做迭代运算，直到满足停止条件取得聚类核心;

3)首先根据(14)式编码hmax个社区核心，再将粒子的适应度值计算出来，然后对粒子群的其他相关参数进行初始化;

5)根据1)至4)得到的聚类核心数，即为网络中包括的社团数目，作为FCM运行的开始条件，然后利用FCM划分网络社区，得到社区结果。

该算法的伪代码如下:

粒子群算法确定最优聚类核心与社区个数阶段:

3 实验结果与分析

3.1 实验参数选取与演变计算

从(1)式可以知道，w1用来调整粒子朝本身最好位置方向移动的步长，w2用来调整粒子朝整体最佳位置移动的步长，且w1∈［0，2］，w2∈［0，2］。当步长bi∈［－bmax，bmax］时(bmax表示粒子一次能移动的最大步长)，才能确保粒子始终在查寻空间内进行查找，并完成演变过程。

任意一个粒子的方位由(2)式计算出来。在社交网络的实际状况下，对新的方位进行模拟，则将粒子的寻找界限约束在查询空间内，这样就能使粒子离开查寻空间的不确定性得到规避。同时，将任意粒子vi(i=1，2，…，m)的适应度与整体通过的最佳位置pc作对比，若整体位置更差，则将其定义为现在的整体最优位置。

3.2 PFCM算法对真实网络的社区划分

为了验证本文算法的有效性，对2个经典的真实社交网络Zachary’s Karate Club［14］和海豚网络(Dolphin network)［6］进行了具体测试，其社区划分结果如图1、图2所示。

图1中，三角形节点集表示一个社区，圆形节点集表示另一个社区。其中节点9的社区归属不正确，其他节点的划分都与具体网络相合。由于优化的聚类核心都是节点1和节点34，则PFCM发现的社团结果与NKFCM划分的结果［10］一样，这也间接证实了PFCM发现社区结构具有稳定性。

图2中，白色正方形节点集表示一个社区，黑色正方形节点集表示另一个社区。节点8、节点40未被分配到准确的社团中，但考虑到节点8、节点40和2个社区的联系都比较紧密，此划分结果也是可以被接受的。

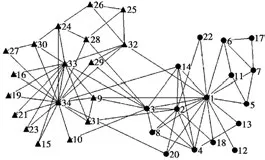
图1 PFCM算法发现Zachary’s Karate Club社区结构的结果Fig.1 Community structure of Zachary’s Karate Club by PFCM

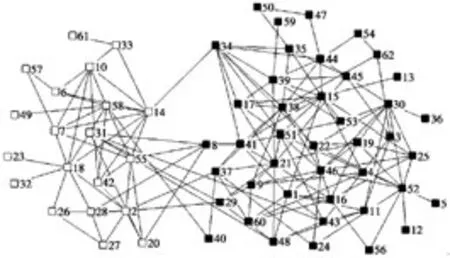
图2 PFCM算法发现Dolphin社区结构的结果Fig.2 Community structure of dolphin network by PFCM

3.3 粒子演变代数与模块度的关系

Newman与Girvan提出了衡量社区划分质量好坏的模块度(modularity)［15］评价函数(又称为Q函数)。当一个社区划分算法实验获得的Q值越高，则该算法发现的社区结构具有较好的结构性;反之则结构性较差。

第k次粒子演变效果与发现网络社区获得的Q值的关系如图3所示。对图3进行分析可得，在粒子的演变历程中，社团划分的效果越来越优良，在第60代粒子演变附近，获取的Q值逐步倾向平稳，此时Q值的改变已不被粒子的演变所引导，这是由于在粒子经历充足的演变次数时，粒子所停靠的全局最好方位不会再变更。

3.4 精确度与算法的质量分析

为了验证PFCM算法的准确性，将该算法与GN算法［16］、快速Newman算法(fast algorithm for detection community structure in networks，FN)［17］、NKFCM算法在真实网络上进行了实验，并做了准确性与Q值的对比，其分析结果如表1、图4所示。

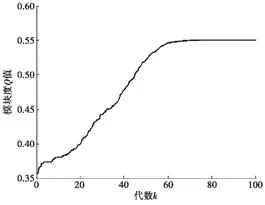
图3 粒子演变代数k与模块度Q值的关系Fig.3.Relationship of particle evolution algebra k and modularity Q’s value

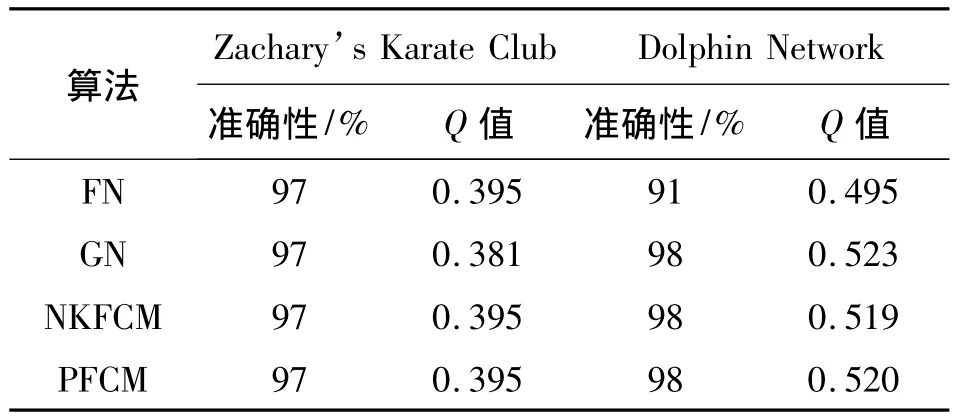
表1 划分的精确度与模块度Q值比较Tab.1 Comparison of accuracy and modularity Q’s value

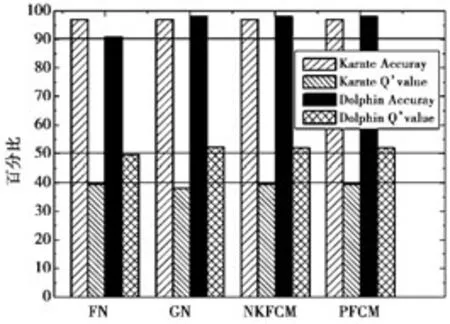
图4 GN，FN，NKFCM，PFCM精确度和模块度对比图Fig.4 Comparison graph of accuracy and modularity for GN，FN，NKFCM，PFCM

通过对表1、图4的分析可知，PFCM算法发现社交网络社区结构的精确度与社区划分获得的模块度值(Q值)都有较好的表现，表明PFCM算法划分社区的精度较高。

3.5 算法的执行效率分析与对比

在k次迭代后可得到网络的社区结构，PFCM算法的时间复杂度为O(k(m+m2))，k表示迭代次数，且k是常数，m表示网络的规模;GN算法的时间复杂度为O(k(m3))，FN算法的时间复杂度为O(m(n+m))，n表示网络的边数;NKFCM算法的时间复杂度为。因此，能够得出后3者的时间复杂度较PFCM的时间复杂度而言，相对较差。

图5是GN算法、NKFCM算法、FN算法、PFCM算法发现不同规模的真实网络和计算机模拟网络的社区结构所花费的时间比较。

分析图5可知，GN算法、NKFCM算法在网络节点数增多时，其执行时间增长迅猛，因此，它们发现大规模的网络社区的实用性较差。伴随网络规模的扩大，对比FN算法和PFCM算法的时间变化曲线，显然，PFCM耗费的时间代价更小，其执行效率更优;在图3的分析说明中，当粒子演变到60代附近时，PFCM已相当靠近最好结果，此时，PFCM的时间复杂度为O(m+m2)，FN的时间复杂度为O(nm+m2)，无论从理论上分析还是从实际运行情况分析都能得出PFCM比FN执行效率更高的结论。

图5 GN，FN，NKFCM，PFCM算法在不同网络规模中的执行时间Fig.5 Runtime of GN，FN，NKFCM，PFCM with different network size

4 结束语

针对目前网络已进入到大规模、大数据时代，使用更高效的算法来发现网络社区结构是大势所趋，因此，借鉴群体智能方法思想，引入粒子群算法，由粒子群优化能得到整体最佳聚类核心，提出了基于粒子群优化与模糊聚类的社区发现算法。首先对粒子优化和演变的流程进行了阐述，接着叙述了算法的整个运作过程，最后将算法在实际社交网络中做了测试，实验结果表明，本文算法有较高的准确性。又以FCM，NKFCM，GN，FN算法的实验结果来比较它们的性能，分析它们的时间复杂度，以不同规模的网络对比其执行时间，得出本文算法的执行效率较高。因此，基于粒子群优化与模糊聚类的社区发现算法具有可行性与有效性。

［1］FALKOWSKI T，BARTH A，SPILIOPOULOU M.DENGRAPH:A Density-based Community Detection Algorithm［C］//IEEE/WIC/ACM International Conference on Web Intelligence.Washington，DC，USA:IEEE，2007，2:112-115.

［2］杨博，刘大有，刘吉明，等.复杂网络聚类方法［J］.软件学报，2009，20(1):54-66.

YANG Bo，LIU Dayou，LIU Jiming，et al.Complex Network Clustering Algorithms［J］.Journal of Software，2009，20(1):54-66.

［3］TVINCEN D，BLONDEL，JEAN-LOUP G，et al.Fast unfolding of communities in large networks［J］.Journal of Statistical Mechanics:Theory and Experiment，2008，10(8):1-12.

［4］淦文燕，赫南，李德毅.一种基于拓扑势的网络社区发现方法［J］.软件学报，2009，20(8):2241-2254.

JIN Wenyan，HE Nan，LI Deyi.Community Discovery Method in Netwoeks Based on Topologic Potential［J］.Journal of Software，2009，20(8):2241-2254.

［5］朱小虎，宋文军，王崇骏，等.用于社团发现的Girvan-Newman改进算法［J］.计算机科学与探索，2010，4(12):1101-1108.

ZHU Xiaohu，SONG Wenjun，WANG Chongjun，et al.Improved Algorithm Based on Girvan-Newman Algorithm for Community Detection［J］.Journal of Rrontiers of Computer Science and Technology，2010，4(12):1101-1108.

［6］QUN L，ZHIMING P，YI G，et al.A new K-means algorithm for community structures detection based on Fuzzy clustering［C］//IEEE International Conference on Granular Computing.［s.l.］:IEEE，2012(11):1-5.

［7］姚丽娟，罗可，孟颖.一种基于粒子群的聚类算法［J］.计算机工程与应用，2012，48(13):29-33.

YAO Lijuan，LUO Ke，MENG Ying.Clustering algorithm based on particle swarm optimization［J］.Computer Engineering and Applications，2012，48(13):150-153.

［8］谢秀华，李陶深.一种基于改进PSO的k-means优化聚类算法［J］.计算机技术与发展，2014，24(2):34-38.

XIE Xiuhua，LI Taoshen.An Optimized k-means Clustering Alorithm Based on Improved Particle Swarm Optimization［J］.Computer Technology and Development，2014，24(2):34-38.

［9］HUA S，GA Z，RUI-SHENG W，et al.Identi?cation of overlapping community structure in complex networks using fuzzy c-means clustering［J］.Physica A，2007，374(1):483–490.

［10］邱新建，薛凤凤，山拜.一种采用粒子群优化的聚类算法［J］.计算机工程与应用，2012，48(10):29-33.

QIU Xinjian，XUE Fengfeng，SHAN Bai.A kind of clustering algorithm applying particle swarm［J］，Computer Engineering and Applications，2012，48(10):29-33.

［11］王国胤，苗夺谦，吴伟志，等.不确定信息的粗糙集表示和处理［J］.重庆邮电大学学报:自然科学版，2010，22(5):541-544.

WANG Guoyin，MIAO Duoqian，WU Weizhi，et al.Uncertain knowledge representation and processing based on rough set［J］.Journal of Chongqing University of Posts and Telecommunications:Natural Science Edition，2010，22(5):541-544.

［12］张光卫，何锐，刘禹，等.基于云模型的演变算法［J］.计算机学报，2008，31(7):1082-1090.

ZHANG Guangwei，HE Rui，LIU Yu，et al.An Evolutionary Algorithm Based on Cloud Model［J］.Chinese Journal of Computers，2008，31(7):1082-1090.

［13］戴朝华，朱云芳，陈维荣，等.云遗传算法及其应用［J］.电子学报，2007，35(7):1419-1424.

DAI Chaohua，ZHU Yunfang，CHEN Weirong，et al.Cloud Model Based Genetic Algorithm and Its Applications［J］.Acta Electronica Sinica.2007，35(7):1419-1424.

［14］CHEN D，SHANG M，LV Z，et al.Detecting overlapping communities of weighted networks via a local algorithm［J］.Physica A:Statistical Mechanics and its Applications，2010，389(19):4177-4187.

［15］王林，戴冠中，赵焕成.一种新的评价社区结构的模块度研究［J］.计算机工程，2010，36(14):227-229.

WANG Lin，DAI Guanzhong，ZHAO Huancheng.Research on Modularity for Evaluating Community Structure［J］.Computer Engineering，2010，36(14):227-229.

［16］黄发良.信息网络的社区发现及其应用研究［J］.复杂系统与复杂科学，2010，7(1):64-74.

HUANG Faliang.Studies on Community Detection and Its Application in Information Network［J］，2010，7(1):64-74.

［17］肖有诰，屠成宇.基于启发式函数的分布式FN算法［J］.计算机系统应用，2012，21(10):122-125.

XIAO Youhao，TU Chengyu.Distributed FN Algorithm Based on Heuristic Function［J］，Journal of Computer Applications，2012，21(10):122-125.