实验室计量器具不确定度的评定
2015-12-15陈少强孙伟强
■文/陈少强 孙伟强
实验室计量器具不确定度的评定
■文/陈少强 孙伟强

为了提升各企业参与市场的竞争能力,通过第三方认证的方式来向顾客(用户)证实其保证产品质量的能力,已是许多企业通常采用的一种手段。特别是在计量器具检定工作中常常应用了测量不确定度的概念,通过计量器具检定,使各企业能与国际惯例在测量结果表征方法上接轨。
过去我们来表述一个产品的测量结果时,通常是采用其绝对误差来表征测量误差的大小,或是通过相对误差来表征其误差的相对变化量,这两种误差的表示法看似准确,其实它是在没有消除测量仪器的误差的影响、人的视觉误差的影响、各种环境因素的影响等影响因素下得出的测量结果。测量不确定度则是在充分考虑各种影响因素后对测量结果给出其分布的范围,给出在这种测量结果下测量准确性的概率。
从上可以看出,在测量不确定度中引入了测量结果的概率和分布的概念,通过置信度的概念来表征测量结果中顾客和企业应承担的风险,像过去我们常接触的正态分布、三角分布、梯形分布、反正弦分布、两点分布状态,在测量不确定度中根据的测量方式和结果不同分别得到了应用。
测量不确定度与测量误差的区别
测量不确定度与测量误差既紧密相连又有区别。测量误差的定义为:“测量结果与其真值之差”,这是一个理想的概念,其真值常常不能确切知道。如若知道其近似值,则可以反号修正值,使其更接近真值。测量不确定度是对影响产生误差的分散性的估计,是描述未定误差特征的量值,是可能估计求出的,“不确定度”一词本身就隐含着为一种可估计的值,不确定度不是指具体的确切的误差值,虽可估计,但却不能用以修正量值。一个量值经修正后,可能会更靠近真值,但其确定度不但不减少,有时反而会更大,这主要还是因为我们不能确切知道真值为多少,仅是对测量结果靠近真值程度或离开真值程度估计而已。
测量不确定度的来源及分类
1、测量不确定度的来源。
“测量不确定度”的定义为:“为合理地表征测量值的分散性,确定测量结果的有效性”。
一是对被测量的定义的不完整或不完善。二是实现被测量定义的方法不理想。三是取样的代表性不够,即被测量的样本不能完全代表所定义的被测量。四是对测量过程受环境影响的认识不周全,或对环境条件的测量与控制不完善。五是对模拟式仪器的读数存在人为偏差。六是测量仪器计量性能上的局限性。七是赋予计量标准的值和标准物质的值不确定度。八是引用的数据或其他参量的不确定度。九是与测量方法和测量程序有关的近似性和假定性。十是在表面上看来完全相同的条件下,被测量重复观测值变化。
2、测量不确定度的分类。
测量不确定度一般有以下几类:
一是标准不确定度:以标准差表示的测量不确定度。
二是合成标准不确定度:当测量结果是由若干个其它量的值求得时,按其它各量的方差或(和)协方差算得标准不确定度,它是测量结果标准的估计值。
三是扩展不确定度:确定测量结果区间的量,合理赋予被测量之值分布的大部分可望含于此区间,扩展不确定度有时也称为展伸不确定度或范围不确定度。引入了(广义的)包含因子是指遵从一定概率的误差限a与标准之比:即K=a/ σ。此值可根据选的概率分布形式查得。
3、测量不确定度的评定。
不确定度有A类和B类两种评定:
不确定度的A类评定为:用对观测列进行统计分析的方法,来评定标准不确定度。
不确定度的B类评定为:用不同于对观测列进行统计分析的方法,来评定标准不确定度。不确定度的B类评定,有时又称为B类不确定度评定。
测量结果不确定度评定的应用
百分表示值误差测量结果的不确定度评定。
测量方法:依据J J G34—2008《指示表(指针式、数显式)检定规程》。
环境条件:温度(20±10)℃,相对湿度≤80%,温度变化≤2℃/ h。
测量标准:指示表全自动检定仪,MPE为±2µm。
被测对象:分度值为0.01mm,行程为≤10mm的百分表。
测量过程:将指示表可靠地紧固在检定仪上,使测杆处于垂直向下或水平的状态,对于指针式指示表,压缩测杆使指示表对零,对于数显式指示表,压缩测杆约0.1m m至0.2m m,将检定仪和指示表置零后开始检定,在测杆正行程方向上,选择相应的检定间隔进行检定直至全行程,继续压缩测杆10分度左右,再进行反向检定。由正行程内各受检点差的最大值与最小值之差确定即为指示表的全量程示值误差。
评定结果的使用:在符合上述条件下的测量结果,一般可直接使用本不确定度的评定结果。
1、数学模型。
指示表的示值误差:
e=Ld-LS+Ld·αd·Δtd-Ls· αs·Δts
式中: Ld——指示表的示值;
Ls——检定仪的示值;
αd、αs——分别为指示表和检定仪的线膨胀系数;
Δtd、Δts——分别为指示表和检定仪偏离20℃时的数值。
令: δα=αd-αs
δt=Δtd-Δts
取:L≈Ld≈Ls
α≈αd≈αsΔt≈Δtd≈Δts
得: e=Ld-Ls+L·Δt·δd+L·a·δt
2、灵敏系数。
灵敏系数:
c1=∂e/∂Ld=1 c2=∂e/∂Ls=-1 c3=∂e/∂α=L·Δt c4=∂e/∂δt=L·α 3、不确定度来源。
一是测量重复性引入的不确定度分量u1;
二是检定仪示值误差引入的不确定度分量u2;
三是指示表与检定仪间线胀系数差引入的不确定度u3;
四是指示表与检定仪间的温度差引入的不确定度u4;
4、不确定度一览表(见表1)。

表1 . 不确定度一览表
5、标准不确定度分量计算。
一是测量重复性引入的不确定度分量u1评定,可以通过连续测量得到测量列(采用A类方法进行评定)。
在相同条件下,对百分表(分度值为0.01m m)中10m m点,用指示表检定仪在重复性条件下连续测量10次,得到测量列10.008m m、1 0.0 0 8 m m、1 0.0 0 7 m m、1 0.0 0 8 m m、1 0.0 0 8 m m、1 0.0 0 8 m m、1 0.0 0 7 m m、1 0.0 0 8 m m、1 0.0 0 9 m m、10.008mm。
实验标准差:
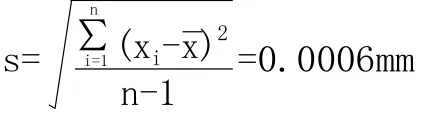
故: u1=s=0.6µm
二是检定仪的示值误差引入的不确定度分量u2评定(采用B类方法进行评定)。指示表全自动检定仪示值误差为:任意10m m范围内为2µm;
三是指示表与检定仪间线胀系数差引入的不确定度u3(采用B类方法进行评定)δd的界限为±2×10-6℃-1,服从均匀分布,k=3,当百分表L=10m m,检定规程要求温度允许偏差Δ t=±10℃,则:u3=1.15×10-6℃-1×L×Δt
=1.15×10-6℃-1×10×103µm× 10℃=0.12µm
四是指示表与检定仪间的温度差引入的不确定度u4(采用B类方法进行评定)。指示表与检定仪间存在一定温度差,以等概率落于区间为±1℃范围内,k=3,百分表L=1 0 m m,线膨胀系数α=11.5×10-6℃-1,则:u4.1=1℃/3=0.58℃
故:u4=0.58℃×L×α=0.58× 10×103µm×11.5×10-6℃-1=0.067µm
6、合成标准不确定度cu。
指示表(分度值为0.01mm):若L=10mm点时:

7.扩展不确定度U
指示表(分度值为0.01m m,L=10mm)时:
取置信因子k=2

百分表用指示表全自动检定仪检定10mm点,其示值误差的扩展不确定度为:
U=4.0µm,k=2
关于测量不确定度的问题很多企业对其应用的极少,多数是一些科研部门和计量主管部门的研究,我们的计量检定机构应更多地了解测量不确定度方面的相关内容,尽快地将过去以误差(准确度)表示的测量结果转换到以上测量不确定度方式表示的测量结果上来,与国际上的误差表示方法接轨,以适应加入“W T O”后的市场规则的要求。
(作者单位:浙江省桐乡市质量技术监督局)

名词解释
什么是测量不确定度
1927年,海森堡在测不准原理的基础上,根据长期的实验,提出了不确定度的关系,又称测不准关系,其后一些学者逐渐使用不确定度来评定测量结果,由于评定方法不一样,评定结果不一致,如有的按3σ评定,有的按σ评定等,使各国在互相利用成果时极为困难,并给各国测量结果的比较带来极大的不便。
1980年,国际计量局在征求各国意见的基础上,提出了实验不确定度的建议书INC—1,该建议得到了国际计量委员会的批准。
1986年,国际标准化组织、国际电工委员会、国际计量委员会、国际法制计量组织成立了国际不确定度工作组,该工作组负责制定国际通用的不确定度标准——指南,经过长期的研究,已制定出“测量不确定度表达指南”(Guide to the Expression of Uncertainty in Measurement),并由上述四个国际组织与国际理论与应用物理联合会、国际理论与应用化学联合会、国际临床化学联合会批准,颁布实施,从而使不确定度的评定与表示有了统一的标准,并使不确定度的研究和应用进入了一个新阶段。
