浅谈数学教学中教师对教材的加工改造

徐洪木

摘要：教材是教师教学用的材料，是专家编写的，水平很高，但不一定是适合学生学习的材料。究其原因，从数学教材来看不外乎是结构严谨、语言科学准确，再加上里面的实例大多不为学生熟悉这三点。

关键词：教材;教师;学生

中图分类号：G632.0     文献标志码：A     文章编号：1674-9324（2015）20-0233-02

教材是教师教学用的材料，是专家编写的，水平很高，但不一定是适合学生学习的材料。究其原因，从数学教材来看不外乎是结构严谨、语言科学准确，再加上里面的实例大多不为学生熟悉这三点。教材改革之后虽然有所改观，但这三点仍然是学生自己不便使用教材的原因。虽然不少学校自己设计学案，但由于水平较低、缺乏研究时间，也无法取代教材。面对这些，一些脚踏实地、不浮躁的教师在课堂上对教材的结构、语言进行加工改造，使学生易于接受。但是这些东西是上不了优质课的，因为评课者不是学生，不会打出高分，但是在教学中他们却能获得优异的教学成绩。道理很简单，语言是教学的传递工具，如何把教材中的知识用学生听的懂的语言表达出来非常重要。除地域不同各有不同的语言特点外，初中学生能听懂的语言的共同特点有三：①简单。文字越少越好。②有趣。适合他们这个年龄段，最起码他们熟悉。③宜浅不宜深。要做到这三点是很难的，也就是我们平常说的深入浅出。教学语言的这些应有的特点，评课者是无法觉察到的：第一，评课者不是学生;第二，他们大多数多年不教学生了。在这篇文章里，笔者以初中数学几处知识点的教学处理方式和片段为例，谈一下对教师教材的合理加工改造。

一种食材无论如何的营养丰富，都要经过厨师的多工序的料理才能成为美味。食材再有营养没有了食客需要的色香味，也不能有效地发挥他的作用。数学教材对于学生就像充满知识营养的食材，必须经过教师的加工才能被学生接受。现行的数学教材是凝聚了课改实验的教育专家、学科专家、教研人员等一级一线教师的智慧，里面的科学性、知识性没有必要去怀疑，但是不同教师用它教出了知识能力不同的学生，千差万别。其中一个重要的原因就是不同的教师对教材做了不同的加工改造。下面从几个方面谈一下自己的看法。

一、对教材中符号的翻译

教育要面向世界，教材里的各种符号都是国际通用的。除了一些学生必须掌握的数学符号，各种单位符号学生非常不适应。在初一应用题的教学中，这些符号成了不少学生的拦路虎。如：t表示吨，h表示小时，dm表示分米;更有一些合成单位，如：km/h表示千米/小时，t/hm 表示吨/公顷，这些使得学生感到陌生，从而影响对题意的理解。一些经验不足的教师经常遇到这样的事：一个感觉难度不大的例题学生却说听不懂。指导学生问“3h”是什么意思，才明白“小时”的符号影响了学生。再如找单项式 的系数时，学生找不出来，也不排除概念不清的原因。但往往解释清楚两点就行了：①π是数不是字母，②此单项式还可写成 与a b相乘的形式：

其实这样的事情在讲解题目以前教师应该想到，提前解决。扫除这种简易的障碍，使学生有精力学习相对重要的数学知识。

二、对教材中一些语句的科学合理的再加工

教材中的语句是严密科学的，但也有不通俗易懂的缺憾。对这些语句的再加工，使之变得易于被学生接受，这是我们教师的事。例如，教材中对方程的解是这样定义的：“能使方程左右两边相等的未知数的值”。这句话虽然字少，但省略了主语，学生对此不好理解。教学中应依据实例演示，再去解释为“一个数代替未知数计算后，如果等号两边的得数相等，那么这个数就是方程的解。”这样学生就比较好理解了。再如教材对中心对称性质的叙述，有一条是“对称点所连线段经过对称中心，而且被对称中心平分。”在教学中，我把它改成了“对称点是任何一对对称点连线的中点，”作为辅助，简洁明了便于识记。一个材料的优劣应看它是不是适合接受它的对象。照本宣科、生搬硬套不会有好的收获。

三、引入实例要从学生身边去找

照抄课本上的实例教学，会使学生有陌生感。如果遇到要解决一个学生不熟悉的实际问题时，可用一个具有相同数学意义的学生熟悉的实际问题来代替，而问题应尽量新奇，不落俗套。如把例题中的人名改成本班的学生姓名，把地名改成学校周围的村镇、车站等，这些都会增加学生的接受兴趣，使得例子生动起来。在七年级方程应用问题中，商品买卖问题学生最难懂。售价、进价、利润、利润率四个量的关系搞得学生晕头转向。每次教学进行到这里我就重复一个虚构的实例：你1元钱买了一只雪糕（冬天就改成烤地瓜）1.5元卖给了你的同桌。你的进价是多少？（学生答1元）售价是多少？（学生答1.5元）赚了多少？也就是利润是多少？（学生答0.5元）赚的钱与进价的比值是多少？也就是利润率是多少？（学生答0.5或者说50%）在最初接触这些量的关系时，这样的例子使学生轻松欣喜，感觉到了利润的产生，这个实例也为学生对此问题的理解起到了重要的作用。再看它们的关系式：售价-进价=利润，利润率=利润/进价，这样就不再陌生了。

四、对教材中的一些知识点的给出形式

教师在教学中要变化不同的表达方式，训练学生多种思维习惯的形成，以提高学生的思维能力。

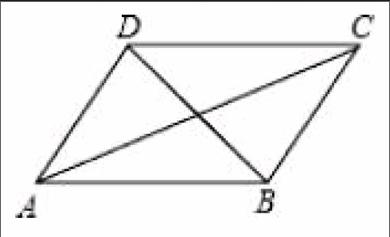
例如：除法法则：除以一个数等于乘以这个数的倒数。要出示式子：a÷b=a×1/b（b≠0）。而对于一元二次方程的求根公式x==Δ=b-4ac≥0因为数学符号多，在教学时，一定要让学生在学会推导后，反复用语言叙述来帮助尽快熟记。在一些需要图形而没有图形的问题中，一定让学生画出图形。这样一方面能培养学生的图像思维，另一方面使问题中的内在规律形象直观，便于学生解决问题。同时，在教学过程中要鼓励学生学会发现教材内容中的关键语句，让学生弄清每个教学用语的确切含义，掌握好数学符号的意义和使用方法，并且让学生对于符号语言、图形语言、文字语言进行相互转化训练。例如，在学习四边形性质时，一条性质既要让学生会用文字语言叙述，也要会用数学符号来表示，并能画出图形指出符号表示的具体位置。比如“平行四边行的两组对角相等”在推导证明后，再让学生练习这样表示“若四边形ABCD是平行四边形，则∠ABC=∠CDA，∠BAD=∠DCB。”并能指出在图中的具体位置，出示的图形不可过于简单，最起码要像下图一样有对角线。

说到这一点，不能不说函数，函数本身有三种变现形式：解析法、图像法、列表法。在解决一个问题时，单纯地一种表示很难让学生明白。以二次函数为例，一个题目的出现本身也是在用不同方法表示的。

例如：（2005·浙江）根据下列表格的对应值，判断方程ax +bx+c=0（a≠0，a、b、c为常数）一个解的范围是（  ）。

A.3

C.3.24

考点：用二次函数图形求一元二次方程的近似值。

分析：根据函数y=ax +bx+c的图像与x轴的交点就是方程ax +bx+c=0的根，再根据函数的增减性即可判断方程ax +bx+c=0一个解的范围。

解：函数y=ax +bx+c的图像与x轴的交点就是方程ax +bx+c=0的根，函数y=ax +bx+c的图像与x轴交点的纵坐标为0;由表中数据可知：y=0在y=-0.02与y=0.03之间，所以对应的x的值在3.24与3.25之间，即3.24

点评：掌握函数y=ax +bx+c的图像与x轴的交点与方程ax +bx+c=0的根的关系是解决此题的关键所在。

以上题目用一种方法是无法表达和解答的。

当然在教学实践中，数学教师要切实体会现代技术的使用，正确运用能帮助学生加深理解、丰富想象、减轻学习难度。但是利用现代技术对教材进行改造加工，主要是在课件的制作使用时还要注意：（1）课件必须依据学生的接受程度而设计，不是课件越玄妙越好，学生必须看得懂。如果课件播放形式过于复杂会影响学生对课件承载知识的掌握。如在教学有理数的大小比较时，用投影放出具体以正负数表示海拔高度的实例就很好，简单明了，直观形象，很容易理解和掌握;有的教师出示股票的变化图像，而且还有动画，理由是有利于激发学生的创造力。虽然在优质课评选和课件制作评选中会获奖，但教学效果却不会好。学生喜欢现代教育技术的媒体课件，好的课件会帮助学生掌握新知识，便于各种能力的提高。但教师也不能因学生的猎奇心理故意制作不利于知识传播和能力培养的课件。（2）课件使用只能是让学生认识规律，不能取代原始的训练。一些基本图形的画法，演算过程的书写都不能用课件代替。

教师和学生是教材的使用者，但学生是通过教师去使用教材的，因为学生驾驭不了教材。学生面对教材就像一个不会做饭的人面对一些上好的食材，何况有的学生还在怀疑教材对于他的意义。因此教师改造加工教材的作用意义是重大的。任何教育理论、教学方法、前辈专家的经验借鉴都离不开教师面对的学生，也离不开教师工作的学校的位置和条件。