基于二阶空间直方图的双核跟踪

张灿龙 唐艳平 李志欣① 马海菲① 蔡 冰①

1 引言

目标跟踪是完成视觉监控、人机交互、车辆导航等诸多视频场景分析和理解任务的基础。已有大量的跟踪方法被报道[1,2]，这些方法可分成四大类：随机性方法[3,4]、确定性方法[5,6]、鉴别分类法[7,8]以及子空间方法[9,10]。随机性方法将目标状态看成随机事件，在贝叶斯框架下，通过滤波来实现目标跟踪， 典型的如粒子滤波跟踪器[3]。而确定性方法通常会先建立一个描述模型匹配度的目标函数，然后将跟踪问题转换为目标函数的寻优问题，典型的如基于核的跟踪器（Kernel-Based Tracking, KBT[5]）。

KBT算法使用基于梯度下降的迭代搜索技术，从而简单快速， 已广泛应用于实时性要求较高的目标跟踪场合。虽然，经过十几年的发展，核跟踪方法已相对成熟，但是， 作为一种轻量级、易实现的算法，它仍广受人们的关注和持续研究[11,12]。原始KBT方法存在空间信息丢失、背景作用弱化以及尺度自适应等问题。针对这些问题， 人们提出了许多改进的方法。文献[13]提出了空间直方图（spatiogram）概念。空间直方图不仅统计每个特征区间内的像素个数，还计算该区间内所有像素点空间分布的均值和方差，从而保持了空间信息。文献[14]指出联合背景信息往往能取得更好的跟踪效果。文献[5]试图通过背景加权直方图的方法消除在目标和背景中同时出现的那些特征的重要性，但这一做法被文献[15]证明是无效的。文献[7]把跟踪问题转变成目标与背景之间的二分类问题， 通过最大化类间距来鉴别目标。但为了获得一个好的分类器，需要大量样本和离线训练，这在实际操作中存在一定的困难。

本文利用空间直方图能保持空间信息的优点，提出了一种基于空间直方图表示的双核式跟踪算法。对于给定的候选目标，本文通过两个指标来判断其是否为真实目标， 指标一是候选目标与目标模板之间的相似度，指标二是候选目标与其邻近背景区域之间的对比度。而目标函数则由这两者的自适应加权组合而成。本文的主要贡献有：提出了目标评判双准则，导出了空间直方图表示下的双核式位移公式，建立了权值的模糊自适应调节机制。

2 二阶距空间直方图

空间直方图[13]是一种带高阶矩信息的广义直方图。零阶矩对应传统意义上的直方图， 而二阶矩直方图则是附加了像素点空间分布的均值和方差信息的直方图。为了行文方便， 以下简称二阶矩空间直方图为二阶直方图。

3 本文提出的算法

众所周知，目标与背景之间的反差越大，就越容易被辨认出来，因此在设计跟踪器的过程应充分利用目标与背景之间的反差特性。无论是早期的背景减跟踪器，还是最近流行的二分类跟踪器[7]，都利用了这一特性。而基于模板匹配的跟踪器，如核跟踪、滤波跟踪和子空间跟踪等，则是利用目标与模板之间的相似度来完成跟踪。研究发现，将目标与模板之间的相似度以及目标与背景之间的对比度进行有机统一，是有益于改善跟踪器性能。

3.1 目标与背景的对比度

为了充分利用背景信息， 我们选择紧绕候选目标、大小为其3倍的环形区域作为有效的背景图像。目标与背景间的对比程度主要体现在颜色特征上，而不是空间结构上，譬如，当目标与背景是颜色完全相同的色块时，它们之间在视觉上应该不存在反差，即对比度应为0，但如果考虑空间结构，则因为一个是矩形，一个是环形，显然对比度不为0，这是与事实不符的。因此，我们在度量目标与背景间的对比度时，只考虑颜色特征。设背景图像的颜色模型为

因为背景图像是环形的， 因此核函数仅在 x ∈[0.25,1]内取非零值。

为了计算目标与背景图像的差异程度， 本文引入延森-香农散度（Jensen-Shannon Divergence,JSD[17]），其定义为

3.2 双核式位移公式推导

同时考虑相似度与对比度对目标评判的影响，则可构建新型目标函数为

其中，0≤α, β≤1为权重系数，用于调节相似度与对比度在目标函数中所占的比重，且有 α +β=1,0≤ ρ（z）≤1。

设目标在前一帧中的位置为 z0。 将式（5）和式（9）代入式（10）中，并在pu（ z0）, ru（ z0） 和 μu（z0）处对目标函数ρ（z）进行泰勒展开，得到线性逼近形式为

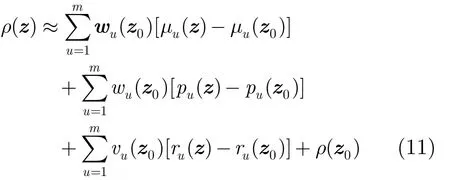
其中

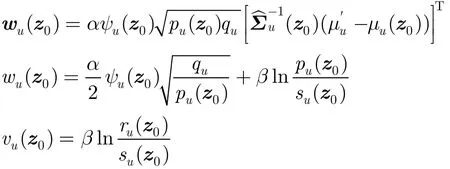
求式（11）中（）ρ z关于z的导数有

其中，gp（x ） = -kp′（x ）, gr（ x ） = -kr′（x ） 。式（14）表明目标的位置是由目标图像与其背景图像共同决定，因为式中存在两个核函数，因此本文叫其为双核式位移公式。在使用Epanechnikov核函数的情况下，式（14）可以进一步简化为

3.3 目标与背景的对比度

可以合理认为在相邻帧之间相似度和对比度不会发生大的变化，因此本文根据前一帧的对比度和相似度值，使用模糊逻辑的方法来自适应地决定当前帧中的权值。模糊逻辑主要由模糊化、模糊规则、模糊推理和解模糊4部分组成[18]，本文采用了单点模糊化、乘积推理和重心解模糊。模糊规则定义为

Rj：如果 e1属于，并且 e2属于,…，并且 el属于，则v属于。其中，Rj为第j条模糊规则，L为总的规则数， {e1, e2,… ,el}和v分别为模糊逻辑的输入和输出。

本文中模糊逻辑的输入为上帧中对比度和相似度的可信度，输出为当前帧中相似度的权值α，而对比度的权值β=1-α。记相似度的可信度分别为

给定目标的模型 h'和它在上一帧中的位置 z0，从位置 z0开始， 根据式（15）递归地搜索目标在当前帧中的最优位置。表2总结了基于二阶空间直方图的双核跟踪（Dual-kernel Tracking Based on Second-order Spatiogram, DTBSS）流程。采用Matlab和MEX混合方式对其进行了编程。

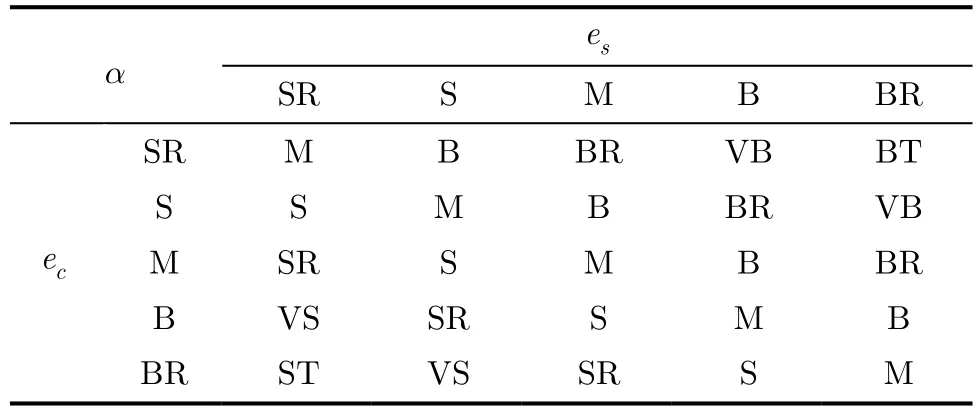
表1 模糊规则基

表2 基于二阶空间直方图的双核跟踪算法

4 实验与分析

本文采用了4段视频来测试DTBSS的性能， 并将它与基于双核的直方图跟踪（Dual-Kernel Based Tracking, DKBT[19]）、基于单核的空间直方图跟踪（Kernel Based Spatiogram Tracking, KBST[16]），增量学习跟踪（Incremental Visual Tracker, IVT[9]）和l1跟踪（l1Tracker, L1T[10]）做了比较和分析。初始目标均由手工标出。初始化。DTBSS, DKBT,KBST算法中的尺度处理采用文献[5]中的方法。实验环境为主频2×3.2 GHz、内存4G的PC机。

4.1 直方图与空间直方图比较

第1个实验通过跟踪视频dollar来比较DKBT和DTBSS。该视频有327帧，每帧大小为320×240，其跟踪结果如图1（a）所示。可以看到从第38帧开始最上面的那张美钞被逐渐折叠，在第51帧中已被折叠，并且整叠钞票在第131帧中被拆成两叠。第134帧中左边那张是被折叠后的原始美钞，右边那张是新露出的美钞，虽然后者外观与第1帧完全相同，但它们并不是同一张钞票。此时，DTBSS并没像DKBT那样跟踪到被折叠美钞，而是跟踪到了与初始美钞外观相似的新美钞。从跟踪结果来说DTBSS是失败了，但从原理上来讲DTBSS比DKBT要更准确，因为DTBSS的空间直方图在描述目标对象时比DKBT的普通直方图多了空间信息。图1（b）和图1（c）分别展示了第134帧中黑色矩形区域的DTBSS和DKBT目标函数值演化曲面，不难看出DTBSS只有一个比较突出的波峰，而DKBT出现了两个幅度非常接近的波峰，这是因为后者所使用的普通直方图没有考虑目标的空间信息，致使美钞折叠前后仍然相似，这与事实矛盾。

4.2 单核与双核比较

第2个实验通过跟踪视频walker来比较KBST和DTBSS。该视频有252帧，每帧大小为640×480，其跟踪结果如图2（a）所示。可以看到第84帧以前两个跟踪器都能稳定地跟踪到walker，但从第84帧开始KBST的跟踪窗发生了漂移，并最终跟丢了目标，而DTBSS始终能稳定地跟踪到运动目标。这主要是因为walker被树干遮挡之后，候选目标与目标模型之间的相似度急剧下降，从而导致KBST搜索失败，而DTBSS却凭借候选目标与其背景之间的对比度，成功地锁定了跟踪对象。图2（b）和图2（c）分别展示了第84帧中黑色矩形区域的相似度与对比度演化曲面，不难看出相似度曲面没有明显的峰值，且对比度峰值远大于相似度峰值，因此该帧中对比度主导了对目标对象的评估。图2（d）中权值α的演化曲线

图1 实验1的测试结果

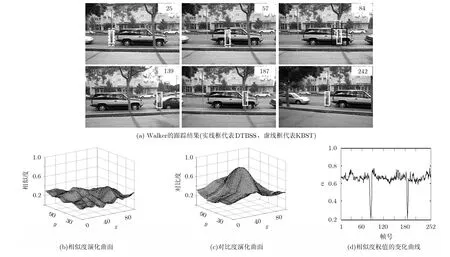
图2 实验2的测试结果

也反映了这一情况，例如，从第81～90帧α的值显著较低，说明此时相似度的可信度要低于对比度的，因此文中的自适应权值调节方法能较好地抑制跟踪过程中不可靠角色。

4.3 与最新跟踪器比较

第3个实验通过跟踪视频doll和panda来比较DTBSS和最新算法IVT, L1T，实验结果如图3所示。可以看到在被跟踪对象未发生旋转和形变时，如图3（a）, DTBSS, IVT和L1T都能准确地锁定目标。但在目标发生较大的旋转和遮挡时，如图3（b）, IVT,L1T分别从第159, 7帧开始跟丢目标。由于在均值漂移（mean-shift）框架下DTBSS是无法解决目标旋转的，而基于粒子滤波框架的IVT却能很容易地处理目标的仿射运动，因此，正如图4（d）所示，尽管DTBSS始终跟上了panda，但其整体准确率要比IVT低。L1T是基于稀疏表示的跟踪算法，虽然也是在粒子滤波框架下实现的，但该文作者提供的源程序并不能处理旋转问题，因此对panda的跟踪效果很不理想。此外，IVT和L1T都引入了在线学习机制，这对处理目标表观变化是有好处的，但同时也带来更新误差的累积问题，随着累积误差越大，它们的跟踪性能也会下降。

4.4 定量比较

表3列举了定量比较结果， 图4展示了逐帧重叠率。不难发现， 与其他跟踪方法相比， 本文所提出的跟踪方法在平均重叠率、平均计算时间和成功率指标上获得了较好的综合性能。

5 结束语

本文将对比度准则引入核跟踪算法中， 并通过综合空间直方图、Jensen-Shannon散度和模糊逻辑等理论， 构建了基于空间直方图的双核跟踪。算法在空间结构保持、背景信息利用和实时性方面实现了有机统一， 是对传统核跟踪算法的有效拓展。对卷入遮挡、旋转、缩放、模糊以及伪目标干扰等变化下的多组目标的跟踪实验验证了本文的结论。未来可研究将双准则目标函数嵌入粒子滤波算法中，以期突破核跟踪框架对缩放、旋转和形变等的约束。

表3 各跟踪方法的定量测试结果

图3 实验3的测试结果（实线框代表DTBSS，虚线框代表IVT，点线框代表L1T）

图4 逐帧重叠率

[1] Zhang S, Yao H, Sun X, et al.. Sparse coding based visual tracking: review and experimental comparison[J]. Pattern Recognition, 2013, 46（7）: 1772-1788.

[2] Wu Y, Lim J, and Yang M. Online object tracking: a benchmark[C]. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Oregon, Portland,USA, 2013: 2411-2418.

[3] Isard M and Black A. Condensation-conditional density propagation for visual tracking[J]. International Journal on Computer Vision, 1998, 29（1）: 5-28.

[4] 程旭, 李拟珺, 周同池, 等. 稀疏表示的超像素在线跟踪[J].电子与信息学报, 2014, 36（10）: 2393-2399.Cheng Xu, Li Ni-jun, Zhou Tong-chi, et al.. Online tracking via superpixel and sparse representation[J]. Journal of Electronics & Information Technology, 2014, 36（10）:2393-2399.

[5] Comaniciu D, Ramesh V, and Meer P. Kernel-based object tracking[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2003, 25（5）: 564-577.

[6] Leichter I. Mean shift trackers with cross-bin metrics[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34（4）: 695-706.

[7] Avidan S. Support vector tracking[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2004, 26（8）:1064-1072.

[8] Zhang K and Song H. Real-time visual tracking via online weighted multiple instance learning[J]. Pattern Recognition,2013, 46（1）: 397-411.

[9] Ross D, Lim J, Lin R, et al.. Incremental learning for robust visual tracking[J]. International Journal of Computer Vision,2008, 77（3）: 125-141.

[10] Mei X and Ling H. Robust visual tracking using l1minimization[C]. Proceedings of the International Conference on Computer Vision, Kyoto, Japan, 2009: 1436-1443.

[11] Fouad B, Lynda D, and Hichem S. Improved mean shift integrating texture and color features for robust real time object tracking[J]. The Visual Computer, 2013, 29（3）:155-170.

[12] Tomas V, Jana N, and Jiri M. Robust scale-adaptive meanshift for tracking[J]. Lecture Notes in Computer Science, 2013（7944）: 652-663.

[13] Birchfield S and Rangarajan S. Spatiograms versus histograms for region-based tracking[C]. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, SanDiego, California, USA, 2005: 1158-1163.

[14] Collins R, Liu Y, and Leordeanum M. Online selection of discriminative tracking features[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27（10）:1631-1643.

[15] Ning J, Zhang L, Zhang D, et al.. Robust mean shift tracking with corrected background-weighted histogram[J]. IET Computer Vision, 2012, 6（1）: 62-69.

[16] Conaire C, O'Connor N, and Smeaton A. An improved spatiogram similarity measure for robust object localization[C]. Proceedings of International Conference on Acoustics,Speech, and Signal Processing, Hawaii, USA, 2007:1069-1072.

[17] Lin J. Divergence measures based on the shannon entropy[J].IEEE Transactions on Information Theory, 1991, 37（1）:145-151.

[18] Liu Y, Tong S, and Chen C. Adaptive fuzzy control via observer design for uncertain nonlinear systems with unmodeled dynamics[J]. IEEE Transactions on Fuzzy Systems, 2013, 21（2）: 275-288.

[19] Zhang C, Jing Z, and Jin B. A dual-kernel-based tracking approach for visual target[J]. SCIENCE CHINA: Information Sciences, 2012, 55（3）: 566-576.