接收端配备滤波器的分布式波束形成技术
2015-12-13陈海华
张 立 陈海华 何 明
1 引言
在无线协作网络中,用户除了从发射节点接收数据外,还可以从多个协作节点接收数据,因而用户即使在配备单个天线的条件下也可实现分集接收,从而提高通信质量和传输速率[13]-。由于发射节点发射的信号经由多个独立的协作节点到达接收节点,因而协作网络中的分集接收通常被称为分布式分集接收,而参与转发信号的协作节点则通常被称为中继节点,相应地,无线协作网络也被称作无线中继网络。为了均衡信道衰减和抑制噪声,近年来人们提出了多种分布式波束形成技术,有效地利用了协作网络的分集接收特性,从而极大地提高了网络的通信质量和通信速率[49]-。
根据不同的应用需求和信道条件,中继节点对所接收到的信号有多种不同的处理方式。最简单的一种是放大而后转发(AF)的中转策略,即中继节点对接收到的信号做适当的幅度和相位调节,然后转发给接收节点[46,10]-。为了抑制由频率选择性信道引起的码间串扰,中继节点可以采用滤波而后转发(FF)的中继数据传输方式[11],即中继节点采用有限长响应(FIR)滤波器对接收到的信号进行处理,然后再转发给接收节点。基于滤波而后转发的中继节点数据传输方式可以有效地均衡发射节点与中继节点以及中继节点与接收节点之间的频率选择性信道衰落。
基于滤波而后转发的分布式波束形成技术在文献[11]中被首次提出,该文献研究由一个发射节点和一个接收节点以及多个中继节点组成的中继网络中的分布式波束形成技术。而文献[11]则提出基于滤波而后转发的多用户中继网络波束形成技术,该文所提波束形成技术考虑多个发射节点和多个接收节点同时通过一系列中继节点发送数据。为了提高网络效率,在文献[13]和文献[14]中提出了双向中继网络的波束形成技术,可以使网络效率提高一倍。基于滤波而后转发的数据传输方式还被应用于多天线的中继网络系统中[15](MIMO relay)。在多天线中继网络中,发射节点、中继节点和接收节点均配备多个天线,在利用分布式分集接收的同时还可以利用传统分集接收的优越性。当无法获取完备信道状态信息时,基于完备信道状态信息的波束形成技术的性能将急剧下降。为保证系统性能,文献[16]提出了具有鲁棒性能的波束形成技术。而文献[17]则研究了基于滤波而后转发的认知无线电中继网络的分布式波束形成技术。
上述文献提出的所有分布式波束形成技术中,在接收节点都只利用了发射信号的一个版本,而其它的时延版本均未加以利用。本文提出一种新的波束形成技术,除了在中继节点上配备FIR滤波器之外,还在接收节点采用FIR 滤波器,最大限度地利用由频率选择性信道引起的时延信号,提高网络性能。在满足中继节点发射功率限额的条件下,中继节点和接收节点上的滤波器将得到联合优化,用以最大化接收节点服务质量(QoS)。该波束形成优化问题由于其高度非线性的特性而难以求解。本文提出一种半封闭解形式的递归算法求取上述波束形成优化问题的近似最优解。在该算法中,各步递归均具有封闭的解析解形式,因而具有较小的计算复杂度。此外,采用本文提出的波束形成技术,可以减短中继节点滤波器的长度至最小,即一个系数,因而可以最大限度地降低中继节点的复杂度,这在实际中是具有相当的应用价值的。仿真结果表明,本文提出的波束形成技术相较于滤波而后转发[11]和放大而后转发的波束形成技术来说,可以极大地提高接收节点的服务质量和网络性能。
2 系统模型
本文提出的波束形成技术基于图1所示的半双工中继网络,该网络由一个发射节点、一个接收节点和多个中继节点构成。所有的节点均只配备一个天线,而各中继节点和接收节点还配一个FIR滤波器。与文献[6,10,11]类似,我们考虑发射节点和接收节点之间无直接有效通道的情况。从发射节点向接收节点发射信号的过程可以分为两个阶段。在第 1个阶段中,发射节点向所有的中继节点广播数据,中继节点接收到的信号经过FIR 滤波后,由各中继节点在第2阶段向接收节点发送。接收节点收到信号后将对其进行线性滤波,从而可以利用信号的多个时延版本,以达到提高接收QoS的目的。本文假设接收节点为中央处理单元,并拥有全部瞬时信道状态信息(CSI)。接收节点利用CSI和接收到的信号确定各中继节点和接收节点上的最优滤波器系数,并通过一个低速率反馈信道反馈给各中继节点。
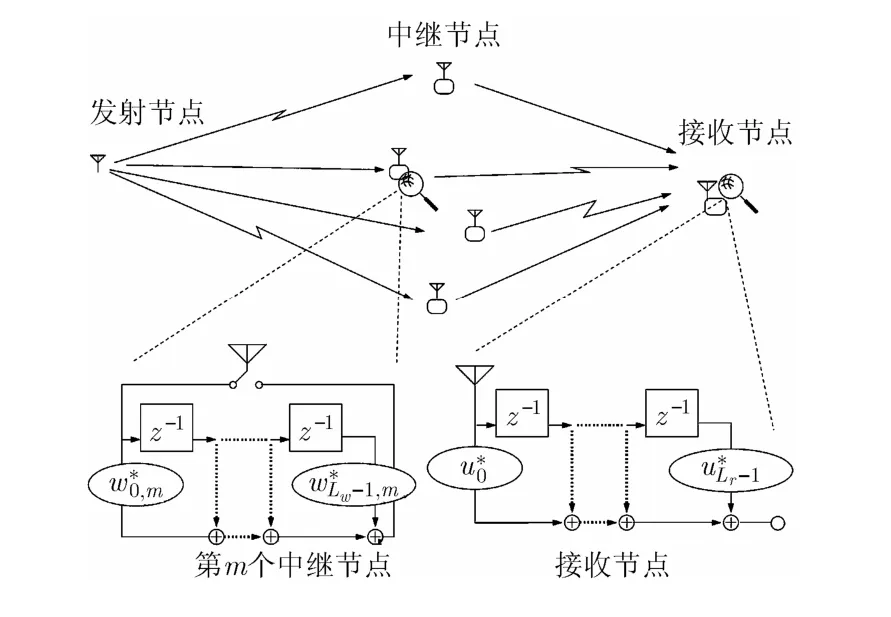
图1 中继节点和接收节点配备滤波器的半双工中继网络
发射节点与中继节点以及中继节点与接收节点之间的频率选择性信道可以用FIR滤波器表示为




其中 υ( n) 是接收节点噪声。把式(2)和式(3)代入到式(4),并做一系列的推导[11],式(4)可以重新写成
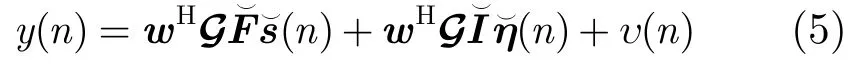
其中

⊗代表Kronecker乘积,IN是一个N×N的单位矩阵,0N×M是一个N×M的全零矩阵。令u≜[u ( 0),u ( 1),… ,u ( Lr-1)]T且 u*代表接收节点滤波器系数向量,其中 Lr是滤波器长度,而(⋅)*表示共轭。由于信道的频率选择性和中继节点的滤波延迟,发射节点信号s( n) 将分布在(Lf+ Lg+ Lw- 2 ) 个采样时刻上,因而设定 Lr≤ Lf+ Lg+ Lw- 2。综上所述,接收节点的滤波器输出为

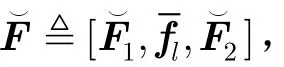

作为本节的结束,我们分别定义式(7)中的期望信号 zs( n)、码间串扰(ISI)zi( n) 和噪声分量 zn(n)为

3 接收端配备滤波器的分布式波束形成技术
本文提出的分布式波束形成技术以最大化接收节点的服务质量为目标,同时满足中继节点发射总功率的限制要求。用信号与干扰噪声比(SINR)作为衡量服务质量的指标。上述波束形成优化问题可写成
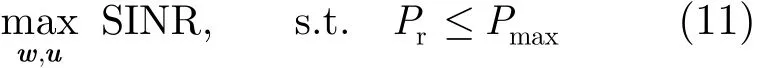
其中rP代表中继节点发射总功率,而maxP 则代表中继节点发射总功率的限额。利用式(3),则第i个中继节点的发射功率为

其中 ei是单位矩阵 IR的第i列,且 Ei=diag {ei}。式(12)可以写成[11]



应用式(8),可以得出
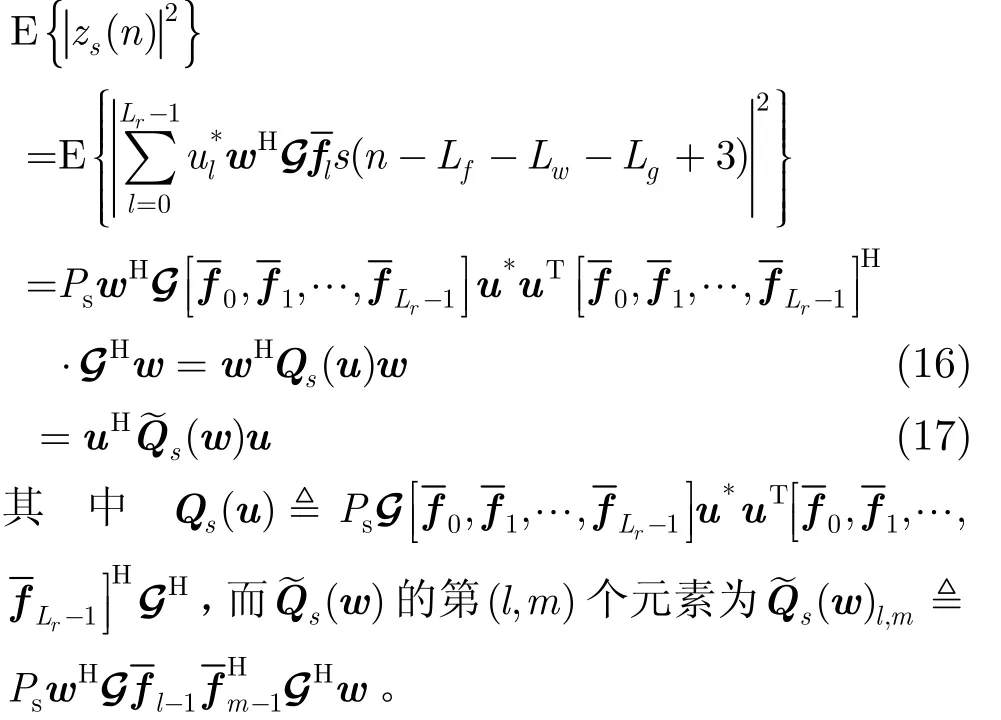
利用式(9),可以得到

矩阵 El-m的大小要求与矩阵Fm和Fl相匹配。应用式(10),则可以得到

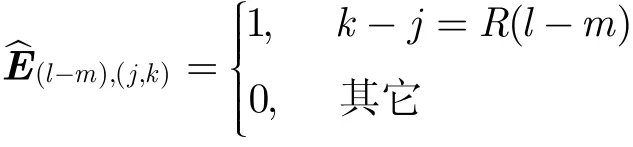
把式(14)-式(16),式(18)和式(20)代入到波束形成优化问题式(11)中,可以得到
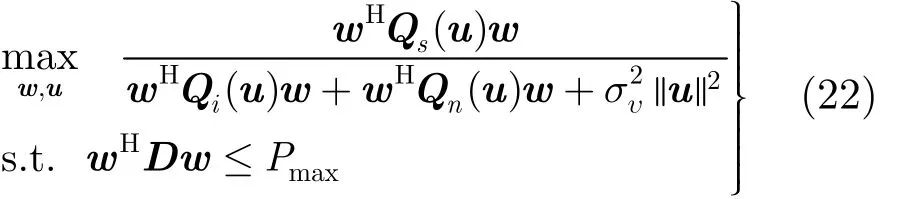
优化问题式(22)中的目标函数是变量w和u的高度非线性函数,因而难以直接求解。本文将通过递归求解两个子问题来求取式(22)的近似最优解,由于两个子问题均只包含变量w和u中的一个,因而易于求解。
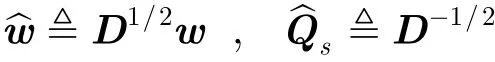

对于任意一个固定值的u来说,问题式(23)的最优解有式(24)形式[5,11]

其中P{⋅}代表一个矩阵的归一化主特征向量,即一个矩阵的最大特征值对应的特征向量。应用定义w︿ ≜D1/2w,则波束形成问题式(23)的最优解和最优接收SINR分别为

其中 Lmax代表一个矩阵的主特征值或最大特征值。
接下来,我们考虑向量w的值固定且满足优化问题式(11)中发射功率条件的情况。把式(14),式(15),式(17),式(19)和式(21)代入优化问题式(11),则可以得到

从问题式(11)及其等效形式式(22)可以看出,问题式(11)中的条件不包含变量u,即中继节点发射总功率的限制条件与变量u无关,因而这里可以略去该条件,从而得到无限制条件的优化问题式(27)。从式(27)中可以看出对向量u乘以任意系数都不会改变该优化问题的目标函数值,因而不失一般性地,我们可以令u2=1。式(27)中优化问题的最优解为[18]

综上所述,从一个u的初始值开始,我们通过递归求解式(23)和式(27)来求取问题式(11)的近似最优解。具体来讲,设u的初始值为0u,通过求解子问题式(23)得到解w。利用该w,求取子问题式(27)的解u,然后再用此解再重新求取子问题式(23)的解,如此重复,直到接收节点的SINR接近平稳。对于一个固定值的u或w来说,由于最优解式(25)和式(28)在各次递归中均是全局最优解,因而通过解优化子问题式(23)和式(27),我们总能找到一个更高 或 相 等的接收SINR,即 S INR ( uN+1, wN+1) ≥SINR ( uN+1,wN) ≥SINR ( uN, wN) ,其中N代表递归次数,因此接收节点SINR的增长得以保证。另外考虑到发射功率固定的情况下,接收节点的SINR值是有限的,因而该递归过程的收敛性也得到了保证。
4 仿真结果
在本文的仿真例子中,我们考虑一个由 R =10个中继节点、一个发射节点和一个接收节点组成的中继网络,该网络处于类静态频率选择性信道中,即信道在一小段时间内保持不变。发射节点与中继节点以及中继节点与接收节点之间的信道长度为Lf= Lg= 5 ,其冲激响应为零均值单位方差的复高斯随机变量。各中继节点和接收节点的噪声具有相等的方差,而发射节点的发射功率比噪声功率高10 dB。为了便于比较,我们在仿真结果中画出了文献[11]中波束形成技术的性能,该波束形成技术也是采用滤波而后转发的中继节点数据传输方法,但是在接收节点无配备滤波器。

图 2显示的是接收节点SINR随着中继节点发射总功率限额 Pmax变化的情况。中继节点滤波器和接收节点滤波器长度如图中所示。当中继节点滤波器长度 Lw= 1 时,滤波而后转发的数据传输协议退化为放大而后转发的数据传输方法。图3描述的是接收节点SINR随着接收节点滤波器长度变化的情况。该例中中继节点发射总功率限额比噪声功率高10 dB,即 Pmax= 1 0。从图2和图3中可以看出,随着接收节点滤波器长度的增加,接收节点的SINR得到了显著地提高。另外,我们还可以看出,本文中提出的分布式波束形成技术性能明显优越于文献[11]中的方法。为了降低中继节点的复杂度,我们可以减短中继节点上滤波器的长度。从图3中可以看出,中继节点的滤波器长度降为 Lw= 1时,增加接收端滤波器的长度至 Lr= 3 ,则可以获得与文献[11]中 Lw= 5 时相当的性能。图4中给出了 Lr= 2 时递归次数随着中继节点发射功率的变化情况。从图 4中可以看出,本文所提递归方法最少的收敛次数小于10次。随着中继节点发射功率的增加收敛速度变慢,递归次数随着中继节点滤波器的增长而增加。
5 结论
本文提出了一种频率选择性信道中中继网络的分布式波束形成技术。为了抑制由频率选择性信道引起的码间串扰,该技术不仅在各中继节点采用有限长响应滤波器,而且在接收节点也配备了一个有限长响应滤波器。通过联合优化中继节点和接收节点的滤波器,使接收节点的服务质量得到优化。上述波束形成问题通过递归求解两个子优化问题而得到近似最优解。文中表明,该递归的收敛性也能得到保证。另外,仿真结果表明本文提出的波束形成技术在性能上明显优于文献[11]中的波束形成器。

图2 SINR随中继节点发射总功率的变化
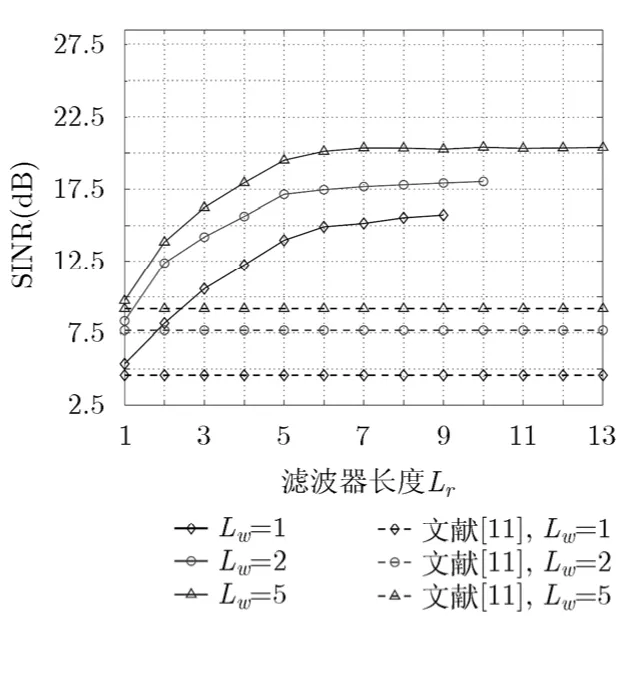
图3 SINR随接收节点滤波器长度的变化

图4 递归次数随中继节点发射功率的变化
[1] Wang H, Luo M, Xia X, et al.. Joint cooperative beamforming and jamming to secure AF relay systems with individual power constraint and no eavesdropper,s CSI[J]. IEEE Signal Processing Letters, 2013, 20(1): 39-42.
[2] Zappone A, Cao P, and Jorswieck E A. Energy efficiency optimization in relay-assisted MIMO systems with perfect and statistical CSI[J]. IEEE Transactions on Signal Processing, 2014, 62(2): 443-457.
[3] 罗苗, 王慧明, 殷勤业. 基于协作波束形成的中继阻塞混合无线物理层安全传输[J]. 中国科学: 信息科学, 2013, 43(4):445-458.Luo Miao, Wang Hui-ming, and Yin Qin-ye. Hybrid relaying and jamming for wireless physical layer security based on cooperative beamforming[J]. SCIENCE CHINA Information Science, 2013, 43(4): 445-458.
[4] Yang Y, Li Q, Ma W, Ge J, et al.. Cooperative secure beamforming for AF relay networks with multiple eavesdroppers[J]. IEEE Signal Processing Letters, 2013, 20(1):35-38.
[5] 王超, 邓科, 庄丽莉, 等. 协作认知网络中鲁棒的分布式波束形成[J]. 西安交通大学学报, 2013, 47(12): 84-89.Wang Chao, Deng Ke, Zhuang Li-li, et al.. A robust distributed relay beamforming algorithm for cooperative cognitive radio networks[J]. Journal of Xi’an Jiaotong University, 2013, 47(12): 84-89.
[6] Wang X, Wang K, and Zhang X. Secure relay beamforming with imperfect channel side information[J]. IEEE Transactions on Vehicular Technology, 2013, 62(5):2140-2155.
[7] Zhang Y, Zhao H, and Pan C. Optimization of an amplifyand-forward relay network considering time delay and estimation error in channel state information[J]. IEEE Transactions on Vehicular Technology, 2014, 63(5):2483-2488.
[8] Hadjtaieb A, Chelli A, Alouini M S, et al.. Performance analysis of selective decode-and-forward multinode incremental relaying with maximal ratio combining[C].Proceedings of the International Conference on Communications and Networking (ComNet), Hammamet,Tunsia, 2014: 1-6.
[9] Gonzalez D C, Santos Filho J C S, and da Costa D B. A distributed transmit antenna selection scheme for fixed-gain multi-antenna AF relaying systems[C]. Proceedings of the International Conference on Cognitive Radio Oriented Wireless Networks and Communications (CROWNCOM),Oulu, Finland, 2014: 254-259.
[10] Fazeli-Dehkordy S, Gazor S, and Shahbazpanahi S.Distributed peer-to-peer multiplexing using ad hoc relay networks[C]. Proceedings of the International Conference on Acoustics, Speech and Signal Processing (ICASSP), Las Vegas, NV, USA, 2008: 2373-2376.
[11] Chen H, Gershman A B, and Shahbazpanahi S. Filterand-forward distributed beamforming in relay networks with frequency selective fading[J]. IEEE Transactions on Signal Processing, 2010, 58(3): 1251-1262.
[12] Schad A, Chen H, Gershman A B, et al.. Filter-and-forward multiple peer-to-peer beamforming in relay networks with frequency selective channels[C]. Proceedings of the International Conference on Acoustics, Speech and Signal Processing (ICASSP), Dallas, TX, USA, 2010: 3246-3249.
[13] Chen H, Shahbazpanahi S, and Gershman A B. Filterand-forward distributed beamformingfor two-way relay networks with frequency selective channels[J]. IEEE Transactions on Signal Processing, 2012, 60(4): 1927-1941.
[14] Liang Y, Ikhlef A, Gerstacker W, et al.. Two-way filter-and-forward beamforming for frequency-selective channels[J]. IEEE Transactions on Wireless Communications,2011, 10(12): 4172-4183.
[15] Kim D, Sung Y, and Chung J. Filter-and-forward relay design for MIMO-OFDM systems[J]. IEEE Transactions on Communications, 2014, 62(7): 2329-2339.
[16] Chen L, Xing C, Fei Z, et al.. Distributed filter-and-forward beamforming for two-way relaying networks under channel uncertainties[C]. Proceedings of the IEEE Vehicular Technology Conference (VTC Spring), Yokohama, Japan,2012: 1-6.
[17] Mohammadkhani S, Hahaei M H, and Razavizadeh S M.Cooperative filter-and-forward beamforming in cognitive radio relay networks[C]. Proceedings of 6th International Symposium on Telecommunications (IST), Tehran, Iran,2012: 170-175.
[18] Shahbazpanahi S, Gershman A B, Luo Z Q, et al.. Robust adaptive beamforming for general-rank signal models[J].IEEE Transactions on Signal Processing, 2003, 51(9):2257-2269.
