窄带干扰条件下含有未知载频的直扩信号的伪码序列估计

沈 斌 王建新

1 引言

直接序列扩频通信是扩频通信的一种主要方式，其信号具有抗窄带干扰能力强、功率谱密度低等特点，可与其他窄带系统构成重叠系统，提高频谱资源的利用率。因此在军事通信和民用通信中得到广泛应用[1,2]，但同时也造成了扩频系统的窄带干扰问题[35]-。在频谱监测、电子侦听等非合作通信系统中，需要对扩频信号进行监测管制，并正确接收。在这过程中，可能受到来自第三方的有意或无意的窄带干扰，其关键问题是要在窄带干扰下对信号进行盲估计，这对扩频通信的民用监测管制和非合作信号侦察干扰具有关键意义。

在窄带干扰下，实际信号含有未知的载频[6,7]。目前大部分干扰抑制的文献没有分析信号本身的信息[810]-，有的只做了简单的描述，没有给出具体分析[11]。本文提出了一种结合矩阵特征分解和线性调频Z变换的算法，可以在分析干扰信号的同时完成伪码序列估计。算法先对接收信号的相关矩阵进行特征分解，然后对特征值应用改进的最小描述长度（MDL）准则找出需要的特征向量，最后对该特征向量应用线性调频Z变换估计载频和伪码序列。

2 信号模型

加性高斯白噪声背景和窄带干扰条件下，接收端的信号可表示为

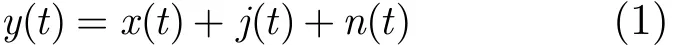
其中，（）x t为载频为'cf的直扩信号经过正交下变频之后的中频直扩信号，（）j t为窄带干扰信号，（）n t为零均值的高斯白噪声。

中频直扩信号可以表示为

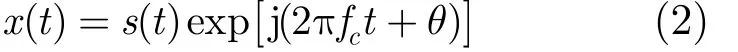
其中，中频信号的载频 fc=- fl, fl为本振频率，θ 为均匀分布的随机相位。基带信号 s（ t） = d （ t） p（ t）,，信息序列 d ∈{+1,- 1 },

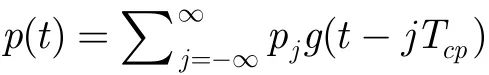
j Tcp为码片宽度，序列长度 N = Tss/Tcp,Tss为伪码周期。文中采用短码方式扩频，即一位信息码由一周期伪码扩展，则 Td=Tss, g（ t）为发射机滤波器与信道冲激响应、接收机滤波器的卷积。

窄带干扰信号j（ t）（以多音干扰为例）可以表示为

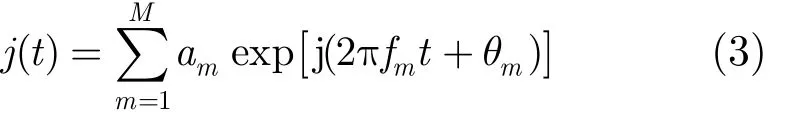
其中，ma为第m个干扰的幅度，M为干扰信号个数，mf为干扰信号频率，mθ为在[,]-π π均匀分布的随机相位。

3 窄带干扰条件下伪码序列的盲估计

3.1 窄带干扰条件下直扩信号的特征分解方法

假设码片速率[7]、伪码周期[12,13]已知，以采样间隔 s cp

TT=对接收信号（）y t进行采样，并且以两倍伪码周期长度分段，数据重叠率为50%，构成观察矩阵：

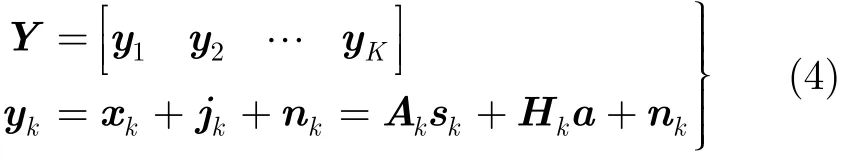
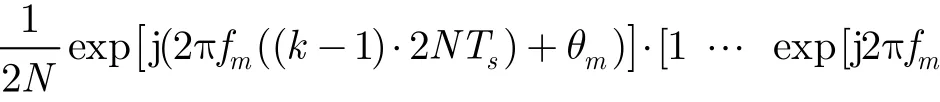
接收信号 yk的分段起始点不一定位于基带信号 sk的伪码序列调制起始点上。假设直扩信号的调制起始点位置为 T0，则 T0∈[0 , N -1]。当T0≠0时，sk可以表示为

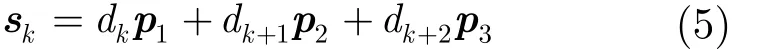
其中，dk,dk+1,dk+2是连续3位信息码。p1,p2,p3是3个向量： p1由长度为 N - T0的伪码序列p的后部和长度为 N + T0的零值组成；p2由长度为 N - T0的零值，长度为N的伪码序列p和长度为 T0的零值组成； p3由长度为 2 N - T0的零值和长度为 T0的伪码序列p的后部组成。将 pi（i= 1,2,3）作幅度归一化，有ui=pi/ pi。由定义可知，ui是正交归一化向量。

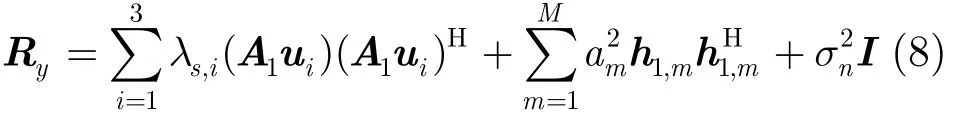
由式（8）可以看出， A1ui和 h1,m都是矩阵 Ry的正交归一化主分量向量。干扰信号特征值为λm=其对应的特征向量为 vm=h1,m。直扩信号 特 征 值 为 λM+1= [ ρ（ N - T0）+ 1 ], λM+2=（ρN+ 1 ）σn2和 λM+3= （ ρT0+ 1 ），一般要比干扰信号的特征值小许多，其对应的特征向量为 vM+1=A1u2,vM+2=A1u1和 vM+3=A1u3。

3.2 伪码序列估计

直扩信号的最大特征向量含有完整伪码信息，因此本文采用改进的 MDL准则估计其位置。基于MDL准则的信息准则函数由对数似然函数和罚函数两部分组成[14,15]，即

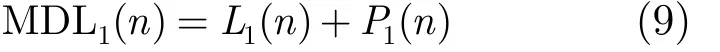
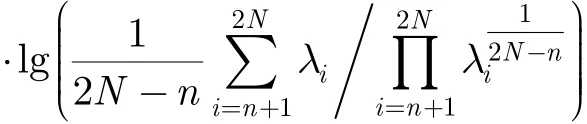
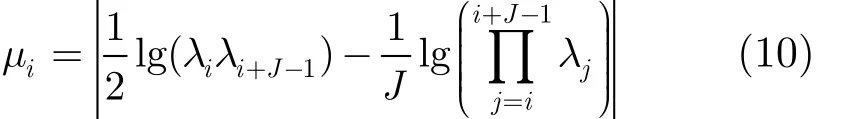
其中，λi为相关矩阵的第i（ i = 1,2,…,2N -J +1） 个特征值，J为平滑窗长度，将序列μi降序排列得到新序列 λi

'。基于新序列的改进的 MDL准则函数和信源数的估计方法为

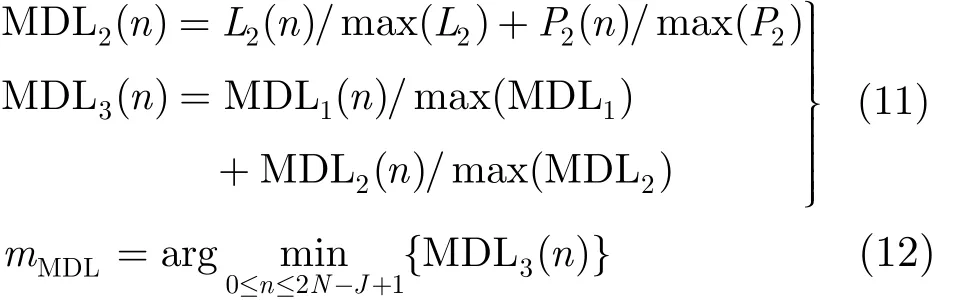
其中，L2（ n） 为对数似然函数，P2（ n） 为罚函数，n=0,1,… ,2N - J +1。

根据式（12）得到信源数的估计，进一步估计伪码序列的位置，定义两个函数：

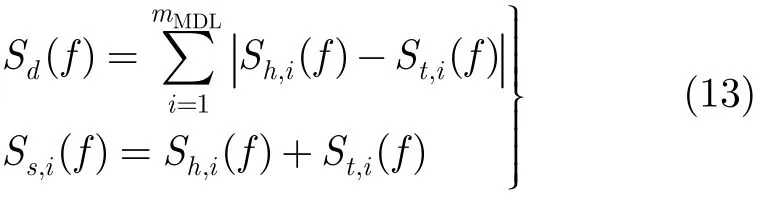
其中， mMDL为信源数的估计， Sh,i（f） 和 St,i（f） 分别是第 i个特征向量的前半段的平方序列 vi2（p）（p=1,2,…, N ）和后半段的平方序列 vi2（p）（p = N +1,N + 2 ,… , 2 N ）的傅里叶变换，即

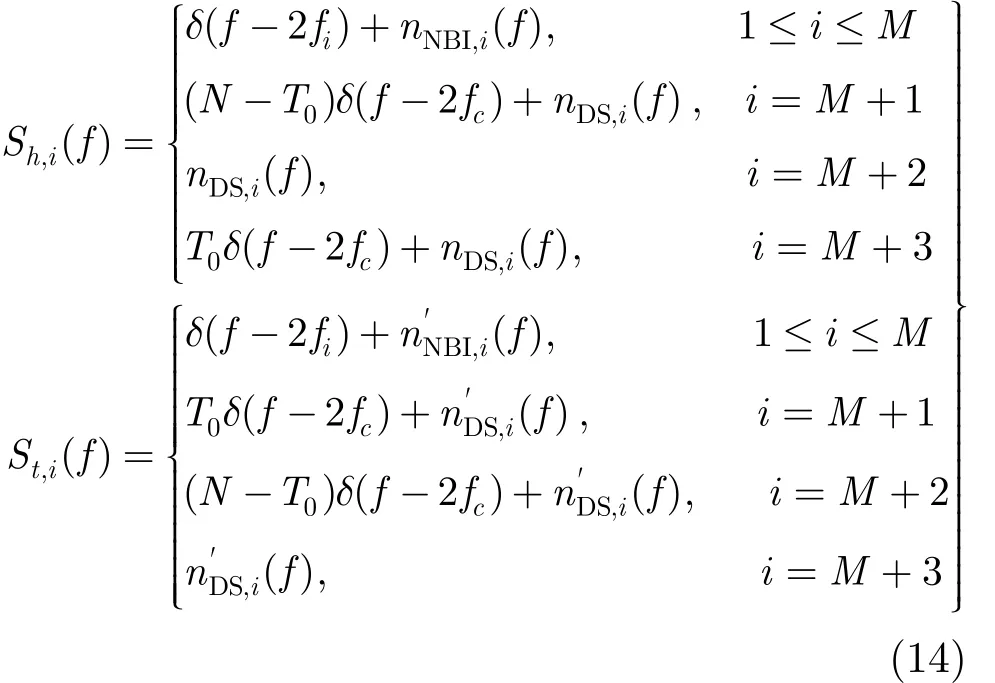
把式（14）代入式（13）有

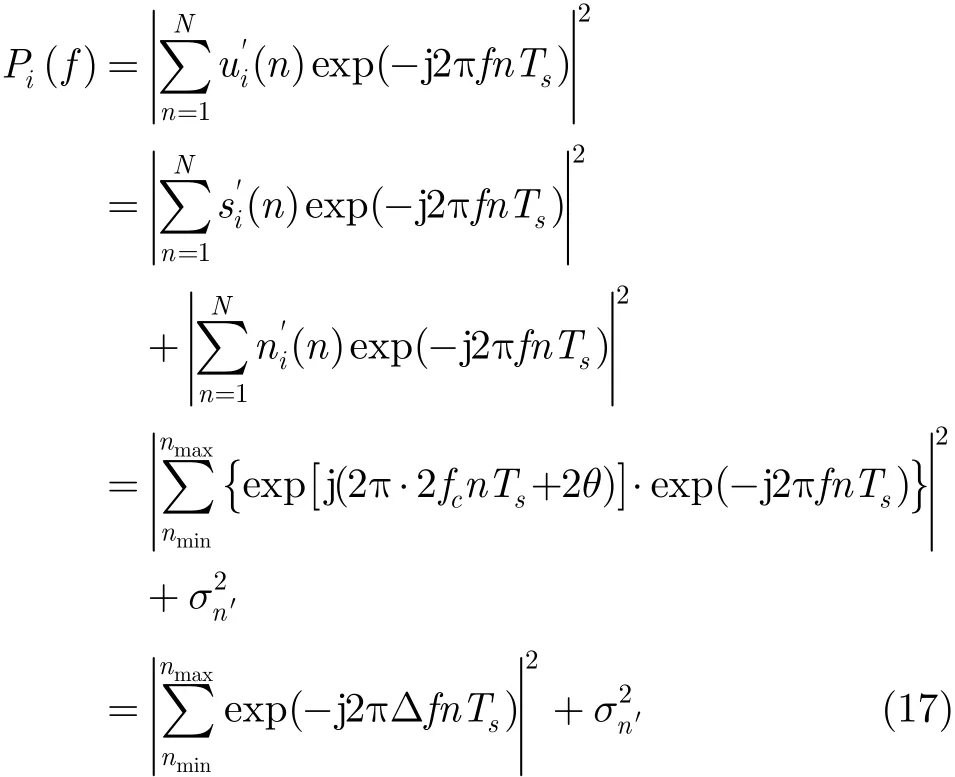
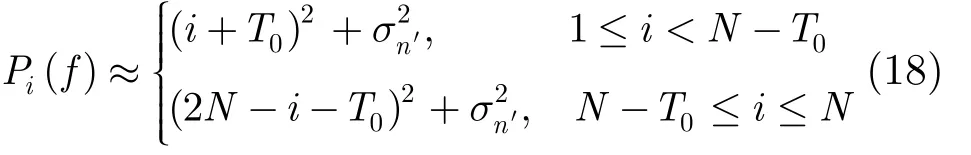
当Δf≈0，即f≈2fc时，将式（17）展开为泰勒级数且略去高阶项，则由式（18）可以看出，令f保持不变，当 i = N - T0时，功率谱达到最大值。

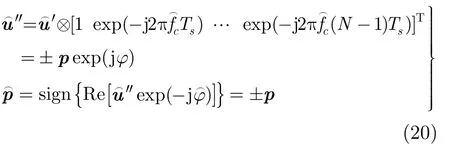
4 算法性能与仿真结果分析

本文仿真中的DSSS信号采用BPSK调制，伪码序列为m序列，采样频率 fs= 3 0 MHz ，参与计算的信号码元数为300。实验中分别使用了下面的3种干扰信号。

（2）调幅（AM）干扰信号：jAM（t） = [ 10 +r（ t ）]⋅exp[ j （ 2πft+θ）]。r（ t）为零均值，2 kHz带宽的基带调制信号，f为干扰信号频率，θ为初始相位。信干比SIR = - 1 0 dB。

（3）调频（FM）干扰信号：

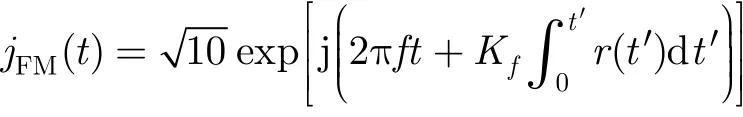
r（ t'）为零均值，2 kHz带宽的调制信号，f为干扰信号频率， Kf为调频灵敏度。信干比SIR = -1 0 dB。

实验1 DSSS信号的伪码序列长度为127，干扰为多音干扰信号。比较MDL准则和改进的MDL准则的性能曲线。信源数估计正确率定义为： pe=P（mMDL= ms）。

图 1可以看出， M DL3函数的性能明显优于MDL1函数； M DL3函数虽然在低信噪比下的估计准确性不如 M DL2函数，但是欠估计问题不明显，而且在高信噪比下拥有理想的性能。综合来看本文采用 M DL3函数作为改进的MDL准则是可行的。

实验2 DSSS信号的伪码序列长度分别为127和1023。考察本文算法在不同干扰信号和不同伪码序列长度下的性能。各项性能指标定义如下：

图2和图3所示是本文算法的估计性能曲线。当伪码序列长度较短时，线性调频Z变换的谱估计性能受限，低信噪比下的估计的性能较差；当伪码序列较长时，低信噪比下的估计性能良好。实际应用中，伪码序列的长度一般都较长，此时本文算法在低信噪比下能正常工作，并且具有估计精度高、稳定性高的优点，具有很强的实用价值。

从图4可以看出，伪码序列长度分别为127和1023时，伪码序列相关系数大于80%的信噪比门限分别为-18 dB和-16 dB。说明本文算法是完全可以在窄带干扰的条件下正确估计出伪码序列的，而且在较低信噪比下也能实现估计。

实验3 DSSS信号的伪码序列长度为1023，干扰为多音干扰信号。考察去除干扰后应用平方倍频法的载频估计性能和本文EVD-CZT法的载频估计性能。去除干扰的方法分别是改进的非线性最小二乘（I-NLS）法[5]，差分门限（D-CT）法[8]和 FFT 重叠变换（FFT-LT）法[10]。

从图5可以看出，本文的EVD-CZT算法充分利用扩频信号本身的特性，受噪声影响较小，载频估计性能最优，其他算法的估计性能相差不大。

实验4 DSSS信号的伪码序列长度为127。考察在不同宽带和不同信干比的调幅信号干扰下去除干扰后应用特征分解的伪码序列估计性能和本文EVD-CZT法的伪码序列估计的性能。去除干扰的方法分别是I-NLS法，D-CT法和FFT-LT法。

图 6（a）中的干扰信号为不同带宽的调幅干扰信号，信干比为 - 1 0 dB，带宽 B W1= 2 kHz , B W2=300 kHz。随着干扰信号带宽的增加，I-NLS法衰减最快，EVD-CZT法其次，D-CT法和FFT-LT法衰减速度最慢；图 6（b）中的干扰信号是带宽为 200 kHz的调幅干扰信号，信干比 S IR1=- 10 dB, SIR2=- 1 6 dB。随着信干比的降低，I-NLS法和D-CT法衰减速度最快，EVD-CZT法其次，FFT-LT法衰减速度最慢。因此EVD-CZT法适用于干扰信号为窄带干扰信号的情况下，并且估计性能受干扰信号功率的影响。在一定的干扰信号带宽和信干比范围内，本文算法的估计性能比其他几种算法要好。

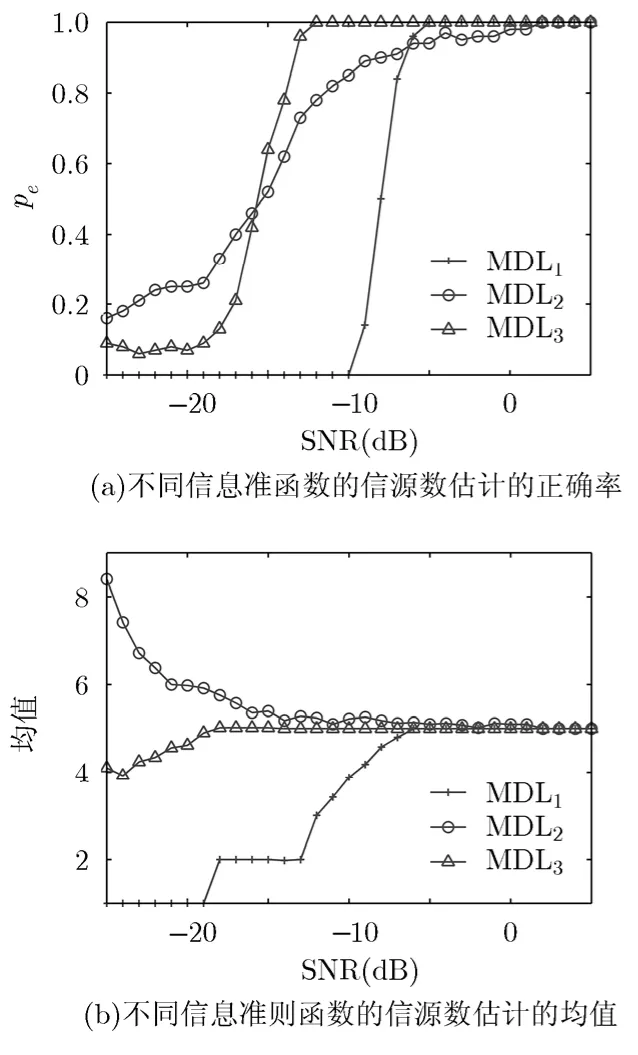
图1 不同信息准则函数的信源数估计的性能曲线

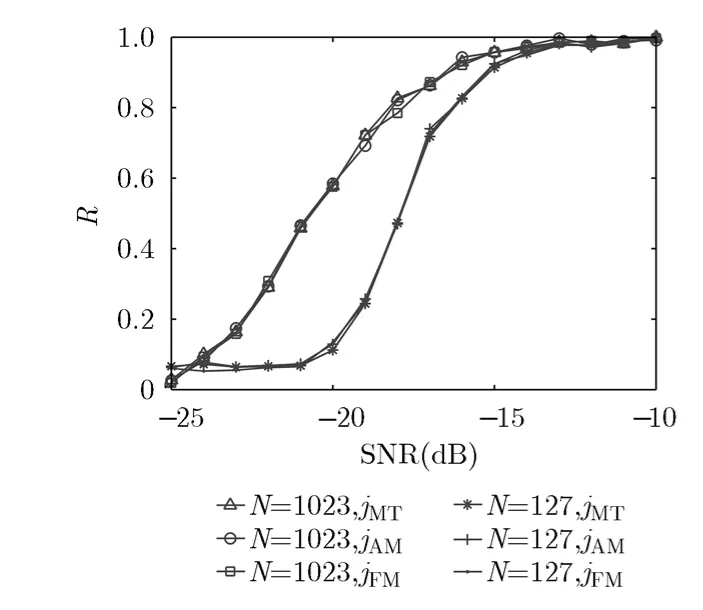
图4 不同伪码序列长度下的伪码序列估计的性能曲线

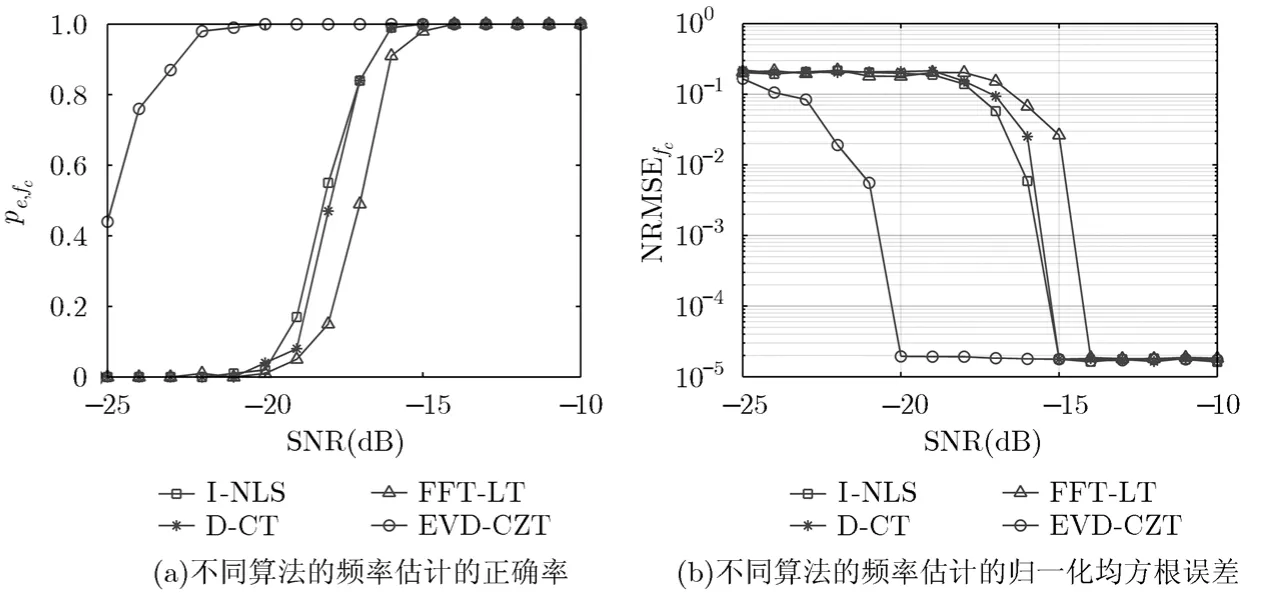
图5 不同算法的载频估计的性能曲线

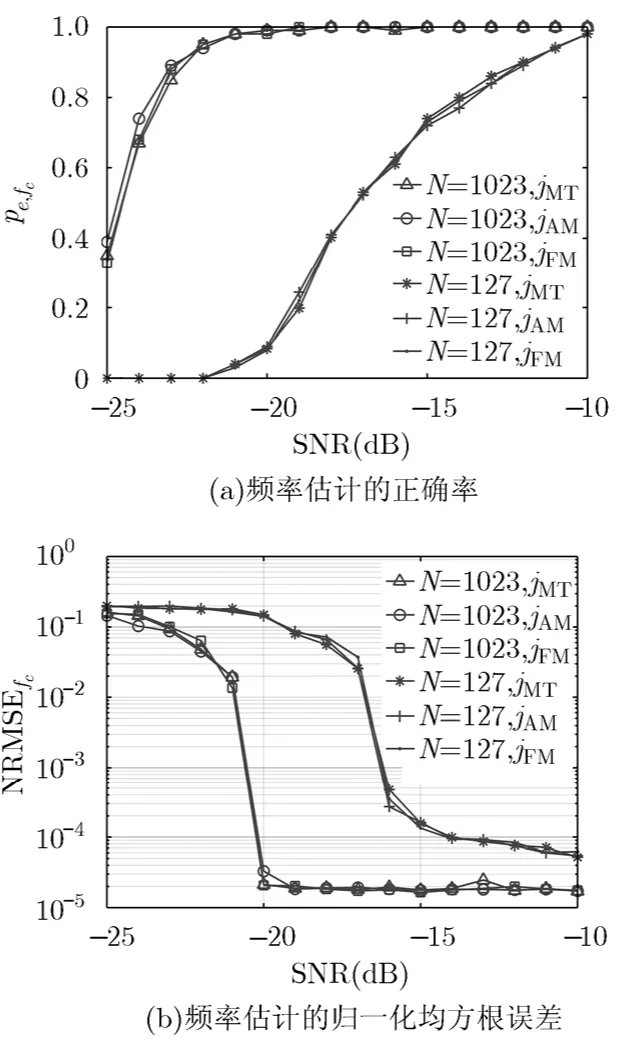
图2 不同干扰信号和不同伪码序列 长度下的载频估计的性能曲线

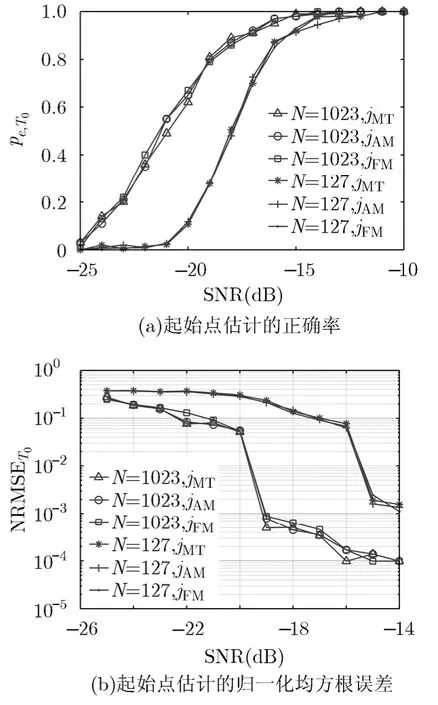
图3 不同干扰信号和不同伪码序列 长度下的起始点估计的性能曲线

图6 不同带宽干扰和不同信干比下的伪码序列估计的性能曲线

5 结束语

为了盲估计窄带干扰条件下含有未知载频的直扩信号的伪码序列，本文提出了一种结合矩阵特征分解和线性调频Z变换的算法。算法先对接收信号的相关矩阵进行特征分解，然后用线性调频Z变换估计载波和序列起始点，最后实现伪码序列估计。仿真表明该算法是十分有效和可靠的，并且较低信噪比下也能实现估计。

[1] Flikkema P G. Spread-spectrum techniques for wireless communication[J]. IEEE Signal Processing, 1997, 14（3）:26-36.

[2] 郭黎利, 孙志国. 通信对抗应用技术[M]. 哈尔滨: 哈尔滨工程大学出版社, 2007: 1-4.Guo Li-li and Sun Zhi-guo. Communication Countermeasure Techniques[M]. Harbin: Harbin Engineering University Press,2007: 1-4.

[3] 罗华. 单音及窄带干扰下DSSS系统处理增益精确分析[J]. 电讯技术, 2014, 54（6）: 713-718.Luo Hua. Accurate analysis of processing gain in direct sequence spread spectrum communication systems under single-tone and narrowband interference[J]. Telecommunication Engineering, 2014, 54（6）: 713-718.

[4] Kasparis T, Georgiopoulos M, and Payne E. Non-linear filtering techniques for narrow-band interference rejection in direct sequence spread-spectrum systems[C]. IEEE Military Communication Conference, McLean, VA, USA, 1991:360-364.

[5] 刘尚峰, 王永民, 郭建新, 等. DSSS时变窄带干扰抑制算法研究[J]. 现代防御技术, 2012, 40（3）: 99-103.Liu Shang-feng, Wang Yong-min, Guo Jian-xin, et al..Research on time variant NBI suppression algorithm for DSSS communications[J]. Modern Defence Technology, 2012,40（3）: 99-103.

[6] Zhang Tian-qi, Dai Shao-sheng, Ma Guo-ning, et al..Approach to blind estimation of the PN sequence in DS-SS signals with residual carrier[J]. Journal of Systems Engineering and Electronics, 2010, 21（1）: 1-8.

[7] 郑鹏, 张鑫, 刘锋, 等. 窄带干扰下基于循环谱的BPSK直扩信号盲检测[J]. 电视技术, 2012, 36（7）: 78-81.Zheng Peng, Zhang Xin, Liu Feng, et al.. Blind detection of DS-SS signal based on cyclic spectrum in narrow-band interference[J]. Video Engineering, 2012, 36（7）: 78-81.

[8] 付卫红, 宋长汉, 黄坤. 基于差分求门限的变换域窄带干扰抑制[J]. 电子与信息学报, 2013, 35（12）: 2960-2965.Fu Wei-hong, Song Chang-han, and Huang Kun.Narrow-band interference suppression in transform domain based on difference-cluster-threshold algorithm[J]. Journal of Electronics & Information Technology, 2013, 35（12）:2960-2965.

[9] 王彪, 孙晓雯. 一种有效抑制窄带干扰的水声直扩信号检测方法研究[J]. 科学技术与工程, 2013, 13（7）: 1784-1788.Wang Biao and Sun Xiao-wen. An effective detection method of underwater acoustic DSSS signals based on narrowband interference suppression[J]. Science Technology and Engineering, 2013, 13（7）: 1784-1788.

[10] 姜恩光, 张福洪. 直扩通信系统抗窄带干扰技术研究与仿真[J]. 电子器件, 2013, 36（1）: 73-75.Jiang En-guang and Zhang Fu-hong. Analysis of narrow-band interference suppression in DSSS[J]. Chinese Journal of Electron Devices, 2013, 36（1）: 73-75.

[11] 马超, 张立民, 林洪文. 窄带干扰下基于子空间跟踪的扩频序列估计[J]. 电子设计工程, 2014, 22（9）: 149-152.Ma Chao, Zhang Li-min, and Lin Hong-wen. The spreading spectrum estimation based on subspace tracking with narrow-band interference[J]. Electronic Design Engineering,2014, 22（9）: 149-152.

[12] 白娟, 张天骐, 余熙, 等. 窄带干扰环境下直扩信号伪码周期估计[J]. 计算机仿真, 2012, 29（2）: 109-114.Bai Juan, Zhang Tian-qi, Yu Xi, et al.. Estimation of PN sequence’s period of the DSSS signals in narrowband interference environment based on spectrum analysis[J].Computer Simulation, 2012, 29（2）: 109-114.

[13] 张天骐, 代少升, 杨柳飞, 等. 在残余频偏下微弱直扩信号伪码周期的谱检测[J]. 系统工程与电子技术, 2009, 31（4）:777-781.Zhang Tian-qi, Dai Shao-sheng, Yang Liu-fei, et al.. Method of spectra for periodic detection of the PN sequence in the weak DS-SS signals with residual carrier[J]. Systems Engineering and Electronics, 2009, 31（4）: 777-781.

[14] Wax M and Kailath T. Detection of signals by information theoretic criteria[J]. IEEE Transactions on Acoustics, Speech,and Signal Processing, 1985, 33（2）: 387-392.

[15] 叶中付, 向利, 徐旭. 基于信息论准则的信源个数估计算法改进[J]. 电波科学学报, 2007, 22（4）: 593-598.Ye Zhong-fu, Xiang Li, and Xu Xu. Improvement of source number estimation based on information theoretic criteria[J].Chinese Journal of Radio Science, 2007, 22（4）: 593-598.

[16] 樊新海, 曾兴祥, 张丽霞, 等. 基于CZT的频谱细化算法及应用[J]. 装甲兵工程学院学报, 2012, 26（1）: 59-62.Fan Xin-hai, Zeng Xing-xiang, Zhang Li-xia, et al.. Algorithm and application of spectrum zoom based on chirp Z transform[J]. Journal of Armored Force Engineering Institute,2012, 26（1）: 59-62.