单源多径路由网络拥塞链路识别

潘胜利 杨析儒 张志勇 钱 峰 胡光岷*

1 引言

随着Internet的发展，互联网越来越多地融入到人们的日常生活中，网络的服务质量也越来越关联着人们的日常生活质量。然而当网络拥塞发生时，网络的整体性能与服务质量将会急剧下降， 伴随网络拥塞而来的高网络时延与高网络丢包率等还可能涉及违反相关服务等级协定（Service-Level Agreement, SLA）中的要求。网络管理者为了及时有效地处理网络拥塞，往往需要首先高效精确地定位出网络中发生拥塞的链路。但由于网络管理者通常并不具有直接操控访问目标（对等）网络设备的权限，使得在目标网络中直接进行拥塞链路定位缺乏实际可操作性。

当无法直接对目标网络进行测量时，网络层析成像[1]成为一种重要的候选网络测量方法。如同医学B超成像不需要直接借助手术来观察内部器官那样，网络层析成像可以在完全不借助于网络内部节点协助的情况下，仅通过在网络边缘进行端到端测量获取路径级性能参数，进而据此来推断网络内部链路相关的性能参数。在早期的网络层析成像研究中，端到端测量常常采用多播测量的方式[1]。但由于多播协议在Internet中的支持度非常有限，目前被广泛使用的是基于单播的测量方式，如模仿多播的背靠背[2]与包群测量方式[3]，用于测量共享路径长度的三明治报文[4,5]，以及单纯地基于单播报文进行路径拥塞状态测量的方式[6,7]等。除了这些端到端测量方式的研究外，还有一些关于如何减少探测报文数目[8]以及如何有效地部署测量监控节点[9]等的讨论。

上述端到端测量方法要么假设端节点对之间只存在一条路由路径[2-8,10,11]，要么假设能够控制和选择测量路径[9,12]。而最近的研究发现表明，网络中的流量均衡现象已经较为普遍。其中，基于流的流量均衡方式（即具有相同五元组流具有相同的路由路径）是网络中较为常见的形式[13]。流量均衡将产生多径路由现象，使得通信节点之间同时存在不止一条可用通信路径，导致端到端探测流的测量路径存在不确定性。文献[14]理论上给出了一个在多径路由场景下可唯一确定端到端测量路径的充分条件，但其基于 K-均值聚类的测量路径识别方法要求事先输入正确的类数目[15]，而不正确的类数目可能会直接导致最终结果不可用。

在通过端到端测量得到路径拥塞状态后，文献[7]通过将所有拥塞路径的拥塞原因归咎于它们的共享路径，提出了最小一致故障集合（Smallest Consistent Failure Set, SCFS）算法来识别网络拥塞链路。文献[12]将SCFS从树型结构推广到一般mesh网络结构，他们结合路由信息提出了用于故障链路定位的Tomo算法。不过这类基于布尔二元模型的拥塞链路定位算法只是单纯地将路径定义为正常和拥塞，并没有有效利用路径性能差异性所带来的其他额外信息，在某些多拥塞链路场景下表现出较低的检测率。例如，一条丢包率为10%的路径相比于一条丢包率为1%的路径，一般认为前者非常可能经历了多条拥塞链路，而非仅仅是一条拥塞链路。此外还有文献[8]结合压缩感知，通过预估出网络链路丢包率来识别高丢包链路的方法，但该方法不能有效确保丢包率的估计精度从而使其具有较高的误检率。

本文将多径路由场景下的网络拥塞链路识别分为如下3个子步骤：（1）端到端测量路径识别。通过利用X-均值聚类算法[15]自适应聚类测量流，提出一种针对基于流级的多径路由测量路径识别的方案；（2）路径状态量化。通过采用LM2丢包率模型[7]获得多个丢包率门限值，进而将路径的不同丢包率量化成相应不同的拥塞状态，将布尔空间扩展成多状态空间[7]；（3）拥塞链路识别。基于线性模型得到由路径与链路拥塞状态构成的线性方程组，以此为约束，将拥塞链路识别问题转化为一个约束最优化问题，提出基于扩展状态空间多径路由网络拥塞识别（Enlarged State Space based Congestion Link Identification, ESSCLI）算法求解该问题。

2 单源多径路由网络模型

将单源多径路由网络的逻辑拓扑建模成一个有向无环图 G = （ V, L），其中V代表网络中的节点，L代表连接这些节点的有向链路。区别于建立在单径路由下的单源树型网络拓扑，多径路由会使得单源网络不再具有树型拓扑结构。将G中的根节点用σ来表示，R代表目的节点集合。令U代表G中的内部节点，那么有V ={σ}∪R∪U。令ζi,j代表连接从节点i∈V到节点j∈V的链路。用j∈d（ i）来表示节点j是节点i的一个下一跳节点，d（ i）是节点i的下一跳节点集合。将根节点σ到目的节点d∈R构成的端节点对表示为Ωd，它们之间的所有子路径集合为= {,… ,…}，其中代表第i条子路径。令Pζi,j表示经过链路ζi,j的所有路径集合。当|Pd|=1时，意味着端节点对Ωd之间是单径路由，否则为多径路由。

令 λ （ ξi, ξj） 表示端到端路径 ξi与 ξj之间的分支节点集合；γ （ ξi, ξj） 表示端到端路径 ξi与 ξj之间的汇合节点集合。同大多数现有方法一样[1]，需假设∀ d 1, d 2 ∈R有 | λ）|=1，且当d1≠d2时γ,）=φ。此外，还假设当d1=d2时，有| γ）|= 1 。这表示达到不同目的节点的路径在分离开后将不能再汇合，而多径路由的子路径之间能且也只能分离与汇合各一次。G中将不能出现度数为2的节点，且不能出现既为分支节点又为汇合节点的内部节点。为了能够唯一确定多径路由各端到端测量子路径，需要假定G满足文献[14]中提出的多径路由拓扑需要满足的充分条件。一个典型的单源多径路由网络的逻辑拓扑图如图1所示。令∈ℕ（d∈R,ℕ代表自然数集合）表示路径∈Pd的拥塞状态，∈ℕ表示链路ζi,j的拥塞状态。令A表示网络中的路由矩阵，其中如果其第i行第j列的元素 aij=1表示第i条路径经过了第j条链路。由于多条拥塞链路会加重路径的拥塞状态，因此使用路径与链路状态的矩阵表达形式Y =[…,,… ], X = [……]以及路由矩阵A，将路径拥塞状态与链路拥塞状态之间的关系用如下线性系统模型进行描述。

图1 单源多径路由网络逻辑拓扑示意图

3 端到端测量与拥塞链路识别

3.1 端到端测量

网络多径路由会使得网络端到端节点对之间存在多条可达的路径[13]。如此需要有两个时隙：第 1个时隙获得每条端到端路径上的测量流信息；第 2个时隙进行端到端路径测量获得路径状态。第1个时隙持续时间很短，一般平均每条探测流发送 200个左右的探测报文即能达到比较良好的路径识别精度[14]，而且可以优先选择在网络运行正常的时候进行该项测量。

3.1.1 多径路由下测量路径识别 源节点到目的节点d之间如果共存在有 n =| Pd|条子路径，那么部署在端节点对之间的m条探测流中，每一条探测流都将有n条路由路径可供选择。不同于文献[14]那样需要假设已知所有子路径的路由概率（即Ωd之间一条子路径成为实际路由路径的概率），我们基于 X-均值聚类算法[15]设计了一个自动增加测量流来达到测量覆盖所有子路径的目的。具体实现流程如下：

输入 单源多径路由网络拓扑G，目的节点d∈R, Ωd间路由路径数目n =|Pd|

（1）在Ωd之间部署m=n条不同五元组的探测流，如 m = 1 ，为路径 ξd选择该探测流 ζd，并终止流程；

（2）按照从每条探测流一个探测包组成包群的模式对Ωd间路由路径进行探测覆盖探测；

（3）计算探测流之间的时延协方差，得到 Cm2个协方差值，采用X-均值聚类算法输出nˆ≤n个类；

（4）如果nˆ ＜n时，增加2（n-ˆn）条不同五元组的探测流到Ωd之间，并从步骤（1）重复开始；

（5）如果nˆ=n时，根据文献[14]所提方法为每条子路径 ξid∈Pd选择择一条探测流ζid，并终止流程。

∈Pd}

通过比较文献[14]基于 K-均值聚类的方法，可以发现一旦出现有子路径上没有被测量流覆盖到的情况时，K-均值聚类算法将无法发现有路径上没有成功部署测量流，并且仍将继续输出与子路径相对应数目的测量流类。而上述基于 X-均值聚类的方法，最主要的改进就是能够确保所有路径上都部署有测量流。关于K-均值与X-均值性能的详实比较与分析可以参见文献[15]，后续性能分析将会略去这一部分。在通过所提方法得到每条路径所对应的测量流后，将要进行第2个时隙的测量工作，即端到端路径丢包率测量[7]。

3.1.2 路径多拥塞状态量化 当在网络路径上如果出现了不止一条拥塞链路时，该网络路径的性能往往比只经过一条拥塞链路的路径要差，如前者可能具有更高的路径丢包率。如此，基于LM2丢包率模型可以得到路径丢包率多门限 T = { 0.01,1-（1 - ℓ ）2,… ,1 - （1 - ℓ）n} ，通过如下量化方法得到路径的拥塞状态：

当路径丢包率ℓ＜0.01时，路径拥塞状态y=0，表示没有路径发生拥塞；而当路径丢包率 ℓ ≥ 0.01时，路径拥塞状态 y ≥ 1 ，表示路径发生了拥塞，拥塞状态值y越大则表示拥塞程度越严重。 经过这样的量化处理后，路径的拥塞状态从传统的二元状态（故障或正常）[7]扩展到如文献[11]中所指出的多元状态空间里，这将有利于后面的拥塞链路识别算法识别出网络中更多的拥塞链路。

3.2 拥塞链路识别

当网络的运行良好时，网络中应该是不存在拥塞链路或者是网络发生拥塞的概率极低。显然，当网络中拥塞链路越多时，网络的整体性能就越差，因而网络的运行状态也就越差。令η代表网络拥塞状态，那么定义网络拥塞状态如式（3）：

即网络拥塞状态是所有网络链路拥塞状态之和。此外还需要说明的一点是，网络链路拥塞状态x的大小有两重含义：一是直接表示该链路的拥塞程度的高低；二则可以是表示该链路可能也是由多条实际拥塞的物理链路组成，因为逻辑拓扑G中所包含的链路为逻辑链路，逻辑链路可以由多条物理链路组成[1]。因此当最终确定了网络中的拥塞链路，实际上更多地是指确定了一个拥塞区间，帮助网络管理员缩小排查范围，使其可以依据该拥塞区间以及结合网络拓扑信息来进一步锁定实际拥塞位置。

3.2.1 基于约束最优化的拥塞链路识别 实际上，网络运营商由于受服务等级协定的约束，其网络的故障率是需要被控制在一个较低水平的。当两条路径拥塞时，我们可以认为它们共享链路上存在拥塞，或者认为所有经过的链路都存在拥塞。如果假设网络中每条链路发生拥塞概率都相同，明显前者发生的可能性将会更高。如此，网络拥塞链路识别的一个合理目标是找到一组拥塞链路，从而使得网络拥塞状态η达到最小。此外，这样一组拥塞链路还需要能够解释端到端观测结果，即需要满足式（1）。通过以式（1）为约束，以最小化网络拥塞状态η为目标，将网络拥塞链路识别问题转化为一个如式（4）所示的约束最优化问题。

根据拥塞状态量化公式（2）可以知道，如果当所得到的链路状态 0x＞ 时，该链路即为拥塞链路。不同于传统的布尔模型仅仅只识别出链路是否拥塞，通过上述约束最优化问题所得到的拥塞链路状态x还能一定程度指示链路的拥塞程度。

3.2.2 ESSCLI算法 传统SCFS算法以及Tomo算法认为所有拥塞路径的拥塞完全是由它们的共享链路发生拥塞所引起的。ESSCLI算法则认为这只能解释部分路径发生的拥塞，并不能解释为什么路径拥塞程度上存在的差异性。事实上，拥塞程度越严重的路径往往预示着其经历了不止一条拥塞链路。因此，ESSCLI并不会在找到公共拥塞链路后停止搜索，反而会进一步依据路径拥塞程度的不同来搜索其他可能存在的拥塞链路。为了求解上述约束最优化问题式（4），首先将对单源多径路由网络拓扑进行分解。

定理 给定单源多径路由网络 G = （ V, L），存在一种图割方法使得得到的两个子图中：其中一个子图的内部节点全是分支节点，另外一个子图的内部节点全是汇合节点。

证明 根据网络模型定义可知单源多径路由网络G是一个连通图。网络G内部节点由分支节点与汇合节点组成，如此则有， U ={λ）|d1, d2∈R} ∪ {γ（）|d1, d 2 ∈R}。但根据单源多径路

如果存在分支节点到汇聚节点这样类型的链路，则表明存在两条经过该链路的路径与，其中d 1 = d 2 ∈R且有 | Pd1|＞ 1 。因为对于两条具有不同目的节点的路径，其 γ）=φ。那么，与在它们最终同时达到 d1时，必然还经过一个汇合节点。如此一来，有 | γ） |≥ 2 ，而这与单源多径路由网络G假设 | γ） |= 1 的要求不相符。因此，即证明网络G中不存在分支节点到汇聚节点这样类型的链路。由分支节点与汇合节点构成的链路类型有：分支节点到分支节点、分支节点到汇合节点以及汇合节点到汇合节点，共3种类型。通过上面的证明可以知道汇合节点只存在由根节点到多径路由目的节点之间（|Pd|＞ 1 ）。因此，将网络G中所有分支节点到汇合节点这种类型的链路分割，必将得到两个部分：一个是以根节点构成的树型拓扑；另外一个是由所有多径路由目的节点{d ||Pd|＞ 1 }构成的森林。由于分割得到的森林是由反向树组成的，因而其内部节点全是汇合节点；显然，由根节点构成的树型拓扑内部节点全是分支节点。至此，定理得证。

输入 G以及其一个分割T与T，路径端到端测量值{yrj|r ∈R,∈Pr}，初始的拥塞链路集合=φ。

（2）∀i∈α ，得到β=d（ i）。如果β ≠ φ，那么∀j ∈ β, xij= m in{y ∈ Pζi,j}，并且对于 ∀ y ∈ Pζi,j，更新 y = y - xij；

（3）更新 α = ∪i∈αd（ i） ，如果 α=φ 则已完成对树型拓扑链路拥塞状态的‿估计，否则执行第（2）步；

（6）对τ'，执行上述第（2）与第（3）步；

（7）将τ'中所有最后一条链路的拥塞状态复制给G中对应‿的分割链路；

4 仿真与性能评估

4.1 仿真场景设置

为了比较所提拥塞链路识别算法的性能，将基于使用网络仿真软件 NS[16]开展相关的网络实验并进行。如文献[13]所指出的那样，基于五元组流的均匀网络流量均衡是网络中较为常见的网络流量均衡类型，本文基于哈希分类算法实现相应的流量均衡模块。根据网络端到端路径数目的多少，仿真网络共分有10种不同的规模（见表1）。在所采用的各仿真网络中，网络内部链路的带宽为10 Mbit/s而网络边缘链路的带宽为5 Mbit/s。内部链路传输等固定时延设定为20 ms，边缘链路则设定为10 ms。网络流量由基于 UDP与 TCP传输协议的通信流组成。其中UDP流为服从帕累托分布，TCP流为FTP文件传输流。网络正常链路的带宽利用率≤75%，丢包率≤0.1%；拥塞链路的带宽利用率≥93%,1%≤丢包率≤1.5%。仿真网络中拥塞链路形成机制为通过加载大量通信流到相应链路上使其拥塞而产生大量网络丢包。

根据文献[13]中所述网络中多径路由比例大小，在各仿真网络中将所有端到端路径中多径路由路径比例设置为40%左右，即|{Pd|d ∈R,| Pd|＞1}|/|{Pd|d ∈R}|≈40%。由于网络一般不会出现大量同时拥塞的链路，因此将拥塞链路的最高比例设置为19%。各不同网络仿真场景重复实验30次，并选取适用于一般 Mesh网络的 Tomo算法[12]和 L1-L2算法[8]与所提ESSCLI算法进行比较。相应评价算法检测性能的指标采用检测率 DR= | ℂ ∩| /|ℂ |，以及误检率 FPR= | {L ℂ } ∪| /|{L ℂ } | （这其中ℂ表示G中实际拥塞链路集合）。

4.2 性能评估

图2与图3分别是ESSCLI, Tomo以及L1-L2算法在网络1（见表1）中不同拥塞链路比例下的检测率DR与误检率FPR性能。根据图2可以看出，所有3个算法的DR随着网络中拥塞链路的增多而呈现出不同程度的降低。其中Tomo算法的DR下降得最剧烈，这是由于其采用了一个较为保守的贪婪策略：将端到端拥塞路径的拥塞原因仅仅归结为它们的共享链路上发生了拥塞。这样的贪婪策略会阻止Tomo算法进一步发现更多的拥塞链路。相反，ESSCLI算法通过对路径状态映射到多元状态来反映路径不同的拥塞程度，并基于不同拥塞状态所带来的额外信息继续搜索拥塞链路，直到所有路径的不同拥塞状态得到解释。而 L1-L2算法也能取得比Tomo算法较好的DR，这主要得益于其线性模型也利用了路径丢包率不同所带来的额外有用信息。但其由于其在链路丢包率估计时所引入的较大误差，可以发现L1-L2算法的DR要比ESSCLI算法低，而且更重要的是，估计不准确的链路丢包率还导致L1-L2表现出非常不理想的 FPR。值得注意的是，Tomo算法正是得益于其保守的贪婪策略使得其具有最小的FPR。尽管如此，随着网络拥塞链路的增多，能够解释端到端路径拥塞的拥塞链路集合也增多了，从而会导致算法的FPR相应地增大，如图3所示。

图4与图5展示的是3种算法当网络链路拥塞比例设定为0.1时，在如表1所示的不同网络规模下的检测率与误检率性能。如图4与图5所示的3种算法的检测率和误检率随着网络规模的增大而呈现正常的波动，但是整体趋势上看，3种算法的性能均都没有明显地表现出随网络规模增大而相应地增大或减小的趋势。虽然网络规模对于检测性能影响不大，但是网络规模大小却直接关联着算法的计算复杂度。表2为在Intel i5-3317U@1.70 GHz中央处理器与4 GB内存计算机上各算法平均运行一次所需的对数计算时间。从表2可以看出，ESSCLI算法由于具有较Tomo大的搜索深度，其计算时间也相应要表现得略高些。但相比于直接搜索的ESSCLI与Tomo算法，L1-L2算法因其迭代搜索方式增加了计算复杂度，导致计算时间明显增加。

表1 仿真网络规模参数

图2 不同拥塞链路比例下的算法检测率

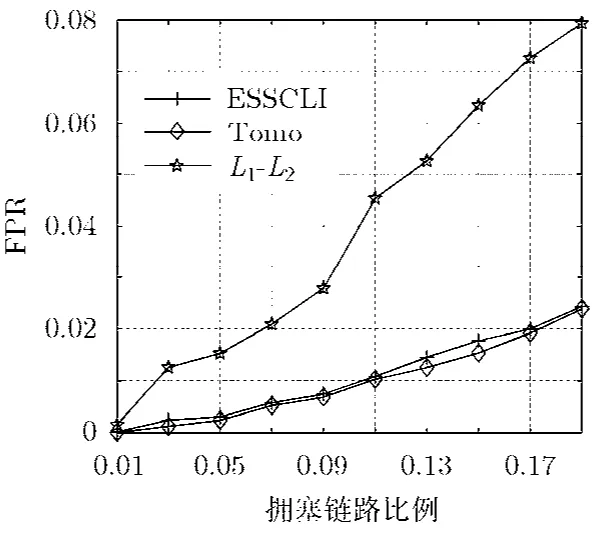
图3 不同拥塞链路比例下的算法误检率

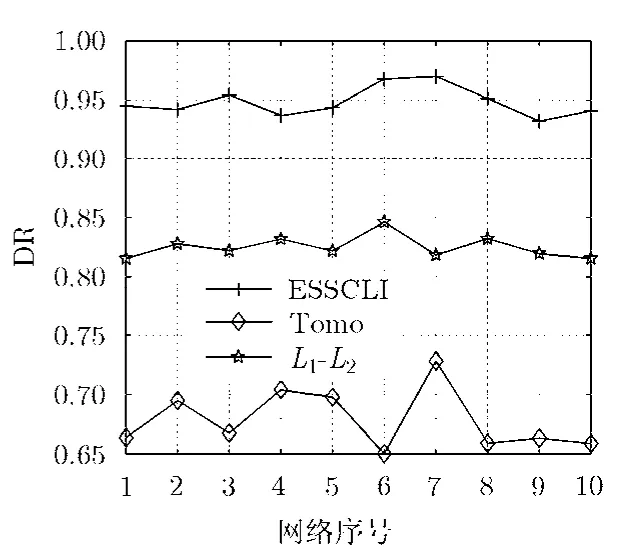
图4 不同网络规模下的算法检测

表2 各算法平均运行一次所需的对数（lg）计算时间（s）

图5 不同网络规模下的算法误检率

5 结束语

基于自适应聚类算法能够规避路径漏测的风险。所提算法能有效地应对多拥塞链路网络场景，且能快速高效地识别出网络中的拥塞链路并且保持较低的误检率。良好的检测性能论证了将拥塞链路识别问题转化为约束最优化问题的合理性。但注意到准确的丢包率测量需要较长的测量周期，研究如何基于路径时延特征来衡量路径拥塞状态进而达到大大缩短测量周期的目的，将是未来可能的一个研究方向。

[1] Castro R, Coates M, Liang G, et al.. Network tomography:recent developments[J]. Statistical Science, 2004, 19（3）:499-517.

[2] Duffield N and Presti F. Network tomography from measured end-to-end delay covariance[J]. IEEE/ACM Transactions on Networking, 2004, 12（6）: 978-992.

[3] Duffield N, Presti F, Paxson V, et al.. Inferring link loss using striped unicast probes[C]. Proceedings of IEEE INFOCOM,Anchorage, 2001, 2: 915-923.

[4] Coates M, Castro R, Nowak R, et al.. Maximum likelihood network topology identification from edge-based unicast measurements[C]. Proceedings of ACM SIGMETRICS,Marina Del Rey, 2003: 11-20.

[5] Malekzadeh A and MacGregor M. Network Topology inference from end-to-end measurements[C]. the 27th IEEE Advanced Information Networking and Applications Workshops, Barcelona, 2013: 1101-1106.

[6] Wei W, Wang B, Towsley D, et al.. Model-based identification of dominant congested link[J]. IEEE/ACM Transactions on Networking, 2011, 19（2）: 456-469.

[7] Duffield N. Network tomography of binary network performance characteristics[J]. IEEE Transactions on Information Theory, 2006, 52（12）: 5373-5388.

[8] Matsuda T, Nagahara M, and Hayashi K. Link quality classifier with compressed sending based on12-ℓℓoptimization[J]. IEEE Communications Letters, 2011, 15（10）:1117-1119.

[9] Ma L, He T, Leung K, et al.. Monitor placement for maximal identifiability in network tomography[C]. Proceedings of IEEE INFOCOM, Toronto, 2014: 1447-1455.

[10] Eriksson B, Dasarathy G, Barford P, et al.. Efficient network tomography for Internet topology discovery[J]. IEEE/ACM Transactions on Networking, 2012, 20（3）: 931-943.

[11] Ghita D, Argyraki K, and Thiran P. Toward accurate and practical network tomography[J]. ACM SIGOPS Operating Systems Review, 2013, 47（1）: 22-26.

[12] Dhamdhere A, Teixeira R, and Dovrolis C, et al..NetDiagnoser: troubleshooting network unreachabilities using end-to-end probes and routing data[C]. Proceedings of ACM CoNEXT, New York, 2007: 18.

[13] Augustin B, Friedman T, and Teixeira R. Measuring multipath routing in the Internet[J]. IEEE/ACM Transactions on Networking, 2011, 19（3）: 830-840.

[14] Pan S, Zhang Z, Yu F, et al.. End-to-end measurements for network tomography under multipath routing[J]. IEEE Communications Letters, 2014, 18（5）: 881-884.

[15] Pelleg D and Moore A. X-means: extending k-means with efficient estimation of the number clusters[C]. Proceedings of ICML, Stanford, 2000: 727-734.

[16] Henderson T. ns-3.21 released[OL]. http://www.nsnam.org/news/ns-3-21-released/. 2014.9.