流量异常检测中的直觉模糊推理方法

范晓诗 雷英杰 王亚男 郭新鹏

1 引言

直觉模糊集合（Intuitionistic Fuzzy Set, IFS）作为模糊集合的泛化理论，因其引入犹豫度参数对客观事物不确定性表述的优势，被学者们广泛研究。直觉模糊推理（Intuitionistic Fuzzy Reasoning, IFR）是模糊理论应用最为广泛的工具，文献[1]将直觉模糊推理与认知图结合，应用于决策支持，文献[2]利用模糊神经网络规则推理对非线性系统进行控制，文献[3]将直觉模糊推理理论应用于目标识别领域，得到了很好的识别效果，文献[4]首次提出了Ⅱ型模糊集理论在模式识别中的应用问题，文献[5]和文献[6]分别将模糊推理运用于故障诊断与图像处理方面，文献[7,8]研究了威胁评估中的直觉模糊推理方法。由此可见，直觉模糊推理理论是一种十分有效的智能信息处理方法。

相似度和包含度是直觉模糊集合间关系的度量，能够有效处理直觉模糊计算问题，是精确问题和模糊问题相互转换的桥梁，许多文献也做了相关研究，文献[9]和文献[10]分别研究了直觉模糊相似度的建模和模式识别应用问题，文献[11]提出了基于包含度的直觉模糊推理方法，并证明给出的公式满足相关公理化定义。这些研究都为直觉模糊推理的应用和推广提供了理论基础，并促进相关领域的创新和发展。

异常检测是网络安全面对的重要问题，网络异常检测通常分为基于统计的检测和基于特征的异常检测，前者通用性能好，但准确度不够理想，后者的优点是准确度高，缺点是特征匹配方法往往效率较低，维护特征数据库的系统开销较大。流量异常检测已有许多基于不同智能计算理论的研究，如统计学原理、免疫计算[12]、支持向量机[13]等，以及一些结合模糊理论的方法，如遗传模糊系统[14]、模糊粒子群算法[15]。传统异常检测方法受到计算复杂度和数据规模的限制，只能选取若干特征属性作为检测指标，对网络流量全局特征的刻画能力有限，尤其是针对连续特征属性，传统精确数据的处理方法，为了提高检测准确率，通常采用模式规模扩充，或者对特征属性进行更细致的划分，这些方法都是以牺牲系统资源为代价，不利于计算方法的进一步优化。直觉模糊理论可以很好描述系统的不确定性和模糊性，通过直觉模糊化将精确数据映射到直觉模糊集中，降低规则库规模，是解决网络流量分类、异常检测问题的新思路。

本文将直觉模糊推理理论应用于网络流量异常检测，充分考虑流量特征描述不确定性和模糊性，并通过实验证明其有效性。

2 异常检测的直觉模糊推理方法

直觉模糊推理的一般过程包括系统输入变量直觉模糊化，推理规则的建立，推理规则合成，输出结果等步骤。运用直觉模糊推理方法进行异常检测时，首先对网络流量特征属性直觉模糊化，然后建立相应的推理规则库，根据推理规则合成，将检测数据输入系统，最后得到输出结果。

2.1 数据直觉模糊化

根据网络流量特征属性，确定直觉模糊系统的隶属度和非隶属度函数。该方法实际上是一个集合映射的过程，将每一个特征属性定义为一个直觉模糊变量，根据特征属性类型确定函数。异常检测KDD99数据集[16]中属性包括离散型和连续型，由于离散型数值各自互斥，没有明显的相关性和相似性，因而采用严格三角隶属度。本文涉及的主要特征属性参数说明如表1所示。

假设某一特征属性A有N个离散属性值，定义第i个属性值对应隶属度函数为（i -1）/n，令犹豫度πA（x）= 0 ，则非隶属度函数为 γA（x）= 1 - μA（x） 。例如，KDD99数据集中protocol_type特征属性包括3个离散变量TCP, UDP和ICMP，根据上述定义，可以计算得到其特征属性函数分别为＜0, 1＞,＜0.333, 0.667＞和＜0.667, 0.333＞。

为了合理描述网络流量分布特性，对于连续型变量，采用高斯型隶属度函数，即

根据式（1），首先对特征属性的论域进行划分，得到特征属性子集，其次确定参数σ和c，得到各个特征变量函数，计算特征属性值对应各个直觉模糊子集的相关输入函数参数，具体步骤为：

步骤 1 根据属性特征划分特征子集 x变化范围,记做 I1,I2,… ,In；

步骤2 设特征属性子集Ai的定义域为[A,B]，确定对应的值域为[C, D]，记映射函数为 f（x, a, b, c）；

步骤3 计算映射参数，D=σ+c，其中c为中心, σ为宽度，a = A +（ B-A）/2，将定义域和值域带入映射函数f=c+（x-a）/b，计算得到b；

步骤 4 多次代入数值检验 x输出分布是否均匀，调整参数和区间划分；

步骤 5 根据式（1）计算隶属度与非隶属度函数。

例如对数据包byte这一特征属性进行直觉模糊化，由于网络中字节数这一指标是非均匀分布，存在大量空数据包，而小数据包变化单位为字节级，而大数据包变化尺度为百字节级甚至千字节级，平均划分论域不能很好描述数据特征。因此，本文对全局论域变尺度划分，得到数据包由大到小分别为B1=[10240,∞ ）, B2=[4096, 10240）, B3=[1024,4096）, B4=[256, 1024）, B5= [1, 256）, B6=0。相应的直觉模糊子集可划分为I1=[0, 0.1）, I2=[0.1, 0.3）,I3=[0.3, 0.5）, I4=[0.5, 0.7）, I5=[0.7, 0.9）, I6=1，隶属度函数如图1所示，特征属性Byte函数参数值如表2所示。根据以上步骤，可以得出特征属性byte输入函数为

表1 KDD99数据集主要特征属性参数说明

同理可以分别得到特征属性 duration, service,flag, urgent的函数，将特征属性service和flag直接线性映射在[0,1]区间，其余连续函数如式（3）和式（4）所示。

图 1 变量byte隶属度函数

最后，定义输出论域U'。将流量检测结果分为5类，normal, Probe, DoS, U2R和R2L，分别对应5个直觉模糊子集[0,0.2], [0.2,0.4], [0.4,0.6], [0.6,0.8]和[0.8,1.0]。

对于U2R和R2L之类的攻击，其数据包与正常连接没有明显区别，所以选择若干基于连接内容和连接时间的特征属性如hot, count。经过特征属性直觉模糊化后，得到异常检测参数变量 D（duration）,S（service）, F（flag）, B（byte）, U（urgent）, H（hot）,C（count），则异常检测推理系统推理规则数 N=Nd×Ns×Nf×Nb×Nu×Nh×Nc= 4×70×11×6×3×3×3=498960。这样的推理规则数量过于庞大，可以进行再次直觉模糊化，例如service特征属性包含70个变量，而csnet_net, ctf, discard, daytime等均对应neptune攻击，将这些可以推理出相同分类结果的服务类型进行聚合，最后得到12个新的直觉模糊子集，约简后推理规则N′=4×12×11×6×3×3×3=85536条，可见利用属性约简的方法可以大大降低推理规则数量，另一方面，这里的N′是理论规则库，并非所有规则都需要生成，通过前期对样本数据的训练，得到理论规则库的一个子集，可进一步缩减规则库的规模，达到提高效率的目的。

2.2 推理规则建立

包含度和强相似度是刻画直觉模糊集合关系的度量，能够有效反应直觉模糊集数据间关系，是直觉模糊推理的基础，本文拟在相关理论的基础上构建基于直觉模糊推理的异常检测方法。

下面给出直觉模糊包含度的相关定→义[11]。定义1 设直觉模糊集上IFS×IFS[0,1]的映射θ满足条件：（1）A ⊆ B ⇒ θ （A, B ）=1,（2）θ（A , φ ） = 0,（3）A ⊆ B ⊆ C ⇒ θ （C, A） ≤ m in{θ（ B, A） , θ（C, B）}。 则 称θ（A, B）为A在B中的包含度，θ为IFS上的包含度函数。

表2 特征属性byte函数参数值

定义2 设R是直觉模糊蕴含算子R（a,b）关于a的非增函数，关于b的非减函数，则为IFS包含度函数，λ是蕴涵算子权重系数，一般取值较小，这里取λ=0.1。包含度函数选择不唯一，通常选择满足定义并易于计算的函数。

定义3 设θ（A, B）为IFS上的包含度函数，则

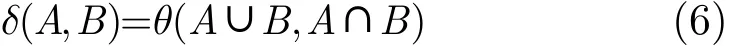
是A和B的强相似度量，相关公理化定义可参阅文献[10]。

根据以上定义和函数公式，表3给出多维多重式规则的基于包含度的直觉模糊推理形式。

表 3 中，i（D）=1,2,…,Nd, i（S）=1,2,…,Ns,i（F）=1, 2,…,Nf, i（B）=1,2,…,Nb, i（U）=1,2,…,Nu,i（H）= 1,2,…,Nh, i（C）=1,2,…,Nc, CFi为直觉模糊推理可信度因子，d, s, f, b, u, h, c是输入特征属性变量，z是输出变量，D,S,F,B,U,H,C是语言前件，即＜d, μDi,γDi＞,d∈D;＜s,μSi, γSi＞,s∈S;＜f,μFi,γFi＞,f ∈ F ;＜b,μBi,γBi＞,b ∈B;＜u,μUi,γUi＞, u ∈U ; ＜ h, μHi, γHi＞, h ∈ H ;＜c, μCi, γCi＞, c ∈ C 。U'为推理后件，即输出论域的直觉模糊子集， ＜ z, μU′j,γU′j＞, z ∈ U '。

表3 基于包含度的直觉模糊推理形式

2.3 推理规则合成

根据以上定义，可以构建出直觉模糊推理方法，具体步骤为：

步骤 1 根据式（5）选取λ和直觉模糊蕴含算子R，若X表示规则特征属性变量，X*表示检测数据特征属性，求得包含度*（,）X Xθ，进而根据式（6）求得强相似度*

（,）X Xδ。步骤 2 利用 Mamdani算子 Rc（A→B）推导输出结果z。则Z =＜ μR,γR＞, z ∈ U '。

δ（X, X*）的推理结果为

i

式中N是特征属性维数。根据上述推理过程，将检测数据在规则库中进行匹配，选择最大强相似度输出直觉模糊集作为推导结果。

3 实验和分析

为验证本文提出的直觉模糊推理异常检测的方法，利用KDD99实验数据集的10%的训练样本集生成一个直觉模糊推理规则库，接着对corrected测试数据集直觉模糊化，得到输入向量，最后经过推理系统得到输出结果，以分类准确率验证方法性能。

3.1 训练规则库

训练样本集的部分数据如表 4所示，每条数据由7维特征属性和1个类别标签构成，根据变量直觉模糊化方法得到相应的推理规则库，部分规则如表5所示。规则推理求解如图2所示，从图中可以看出，前4条规则可以合并为1条，由此可见直觉模糊化具有化简规则库的作用。

3.2 推理步骤

实验 1本文首先验证推理方法的有效性，以corrected测试数据集随机选取的9条数据为例，如表6前8列所示，首先对检测数据进行直觉模糊化，得到如下输入向量：

I1= [1, 0.9130, 0.1818, 0.7820, 1, 0, 0.0020], I2=[1, 0.9130, 0.1818, 0.7820, 1, 0, 0.0040], I3= [1,0.7470, 0.1818, 0.3005, 1, 0, 0.9785], I4= [1, 0.7470,0.1818, 0.3005, 1, 0, 0.9941], I5= [1, 0.7470, 0.1818,0.3005, 1, 0, 0.9980], I6= [1, 0.7470, 0.1818, 0.7141,1, 0, 0.0020], I7= [0.7880, 0.1660, 0.1818, 0.9586, 1,0, 0.0040], I8= [1, 1, 0.5454, 1, 1, 0, 0.0040], I9= [1,1, 0.5454, 1, 1, 0, 0.0020]。

表4 训练样本数据集

表5 推理规则库

图 2 规则推理图

接着将向量输入规则库，分别求出与每条规则的强相似度，取最大强相似度输出结果Z*，得到推理结果O1=0.2, O2=1.0, O3=0.6, O4=0.6, O5=0.6,O6=0.6, O7=0.4, O8=0.8, O9=0.8，最后反推出所属类别label，结果如表6第9列所示。

经过与原始标签对比，9条数据分类结果正确，通过实验1可以看出，基于该直觉模糊推理系统的异常检测方法是有效的。

3.3 实验结果与分析

实验 2 对比本文方法与其他相关方法，测试数据集corrected包括约300000条数据，为测试直觉模糊推理方法的分类效果，从中随机选择 10000条数据，其中包括5227条正常数据和4773条异常数据，数据分布情况如表7第1列所示。分别对测试数据进行8次实验取平均值。前3次实验得到分类结果及8次平均正类正确分类率TP和正类错误分类率FP值如表7所示。

表6 检测数据集

实验分类正确率结果与相关经典方法比较，根据文献[17]的实验部分，对比Wenke Lee的异常检测方法，SVM, BP network，免疫算法[12]和遗传模糊系统（基于Michigan算法）[14]方法，取平均分类正确率如表8所示。

通过表8可以看出，基于包含度的直觉模糊推理方法在网络流量异常检测中具有良好的表现，由于DoS攻击具有明显的特征属性，各种异常检测方法均能达到良好的检测结果，对于Probing攻击，本文提出的方法仅较 SVM 和 BP network略有逊色，仍然具有较高的检测率，R2L和U2L攻击特征属性并不明显，不同方法特征提取的不同导致检测结果差异较大，而基于直觉模糊推理的方法有规则库作为支持，对该类攻击检测结果均能达到90%以上，从而说明本文方法的有效性和泛化能力。

4 结束语

本文针对网络流量异常检测问题，提出了基于直觉模糊推理的异常检测方法，将直觉模糊理论针对不确定性和模糊性描述能力强的特性与网络流量特征属性相结合，进一步提高了网络流量的刻画能力。通过 KDD99标准数据实验，验证了本文方法的可行性，同时与其他相关方法比较，对 R2L和U2L等特征属性不明显的攻击取得较好的检测效果，对直觉模糊理论在网络信息安全领域应用进行了有益的探索。直觉模糊理论在异常检测方面的研究目前还停留在线下检测，如何应用于线上即时检测还需要进一步深入研究。

表7 异常检测结果

表8 算法对比结果（%）

[1] Dimitris K and Elpiniki I. Intuitionistic fuzzy reasoning with cognitive maps[C]. Proceedings of the IEEE International Conference on Fuzzy Systems, Taipei, China, 2011: 821-827.

[2] Chen Cheng-hung. Compensatory neural fuzzy networks with rule-based cooperative differential evolution for nonlinear system control[J]. Nonlinear Dynamics, 2014, 75（1）: 355-366.

[3] Lei Yang, Lei Ying-jie, and Kong Wei-wei. Technique for target recognition based on intuitionistic fuzzy reasoning[J].IET Signal Processing, 2012, 6（3）: 255-263.

[4] Mitchell H B. Pattern recognition using type-II fuzzy sets[J].Information Sciences, 2005, 170（2/4）: 409-418.

[5] Hong Peng, Jun Wang, Mario J P J, et al.. Fuzzy reasoning spiking neural P system for fault diagnosis[J]. Information Sciences, 2013, 235: 106-116.

[6] Luigi L and Larbi B. Using multiple uncertain examples and adaptative fuzzy reasoning to optimize image characterization[J]. Knowledge Based System, 2007, 20（3）:266-276.

[7] 雷英杰, 王宝树, 王毅. 基于直觉模糊推理的威胁评估方法[J].电子与信息学报, 2007, 29（9）: 2077-2081.Lei Ying-jie, Wang Bao-shu, and Wang Yi. Techniques for threat assessment based on intuitionistic fuzzy reasoning[J].Journal of Electronics & Information Technology, 2007, 29（9）:2077-2081.

[8] 雷英杰, 王宝树, 王毅. 基于直觉模糊决策的战场态势评估方法[J]. 电子学报, 2006, 34（12）: 1275-1279.Lei Ying-jie, Wang Bao-shu, and Wang Yi. Techniques for battlefield situation assessment based on intuitionistic fuzzy decision[J]. Acta Electronica Sinica, 2006, 34（12）: 1275-1279.

[9] Hwang C M, Yang M S, Hung W L, et al.. A similarity measure of intuitionistic fuzzy sets based on the Sugeno integral with its application to pattern recognition[J]. Information Sciences, 2012, 189: 93-109.

[10] Boran F E and Akay D. A biparametric similarity measure on intuitionistic fuzzy sets with applications to pattern recognition[J]. Information Sciences, 2014, 255: 45-57.

[11] 王毅, 刘三阳, 张文, 等. 基于包含度的直觉模糊相似度量推理方法[J]. 系统工程与电子技术, 2014, 36（3）: 497-500.Wang Yi, Liu San-yang, Zhang Wen, et al.. Intuitionistic fuzzy similarity measures reasoning method based on inclusion degrees[J]. Systems Engineering and Electronics,2014, 36（3）: 497-500.

[12] 严宣辉. 应用疫苗接种策略的免疫入侵检测模型[J]. 电子学报, 2009, 37（4）: 780-785.Yan Xuan-hui. An artificial immune-based intrusion detection model using vaccination strategy[J]. Acta Electronica Sinica, 2009, 37（4）: 780-785.

[13] Kuang F J , Xu W H, and Zhang S Y. A novel hybrid KPCA and SVM with GA model for intrusion detection[J]. Applied Soft Computing, 2014, 18（5）: 178-184.

[14] Abadeh M S, Mohamadi H, and Habibi J. Design and analysis of genetic fuzzy systems for intrusion detection in computer networks[J]. Expert Systems with Applications,2011, 38（6）: 7067-7075.

[15] Karami A and Zapata M G. A fuzzy anomaly detection system based on hybrid PSO-Kmeans algorithm in content-centric networks[J]. Neurocomputing, 2014, 149（3）:1253-1269.

[16] Hettich S and Bay S D. KDD cup 1999 data[OL].http://kdd.ics.uci.edu/databases/kddcup99/kddcup99.html,1999.

[17] Guo S Q, Gao C, Yao J, et al. An intrusion detection model based on improved random forests algorithm[J]. Journal of Software, 2005, 16（8）: 1490-1498.