初中数学归纳法教学方法浅探
2015-12-13唐克明
■ 唐克明

归纳法是初中数学重要的思维方法之一,它和演绎法、类比法、待定系数法、换元法、数形结合法等都归属于数学方法性知识。新版的《初中数学教学大纲》对归纳法的掌握提出了明确的要求:要“会用归纳、演绎和类比进行推理”。可见,初中数学教师要重视教学归纳法的教学。
一、实验建模,让学生感悟归纳法的思想
关于归纳法的初始教学,笔者认为可采用实验建模的方法,引导学生做实验,经历观察——归纳——猜想的过程,由感性认识上升到理性认识,让学生易于理解和接受,从而提高教学效率。请看以下二个实验。
实验一:
【实验过程】
1.准备十盒长方体香烟;
2.按顺序将香烟排成立起来的长方体,每两个长方体间的距离一定,确保前一个长方体倒下,后一个长方体必定倒下;
3.实验开始,推倒第一个长方体,让学生观察结果。从第二个,第三个,……多次重复上述实验。
【实验结果】
推倒第n个(n=1或2等),从第n个以后的所有长方体依次倒下。
以上过程,通过引导学生做实验,观察香烟倒下的现象,归纳倒下的规律,猜想出一般性结论。像这样根据某类事物中每一个对象的情况或者根据对某类事物中的一部分对象的情况而作出关于该类事物的一般性结论的方法,叫做归纳法。归纳法实际上要经历一个观察——归纳——猜想——论证的过程。初中只要求学生达到猜想层面水平。
实验二:
【实验过程】
1.准备一米长的细线和剪刀;
2.将细线对折,剪去一半,提问剩余的是几分之几?
3.将余下细线,再对折,剪去一半,提问剩余的是几分之几?
4.重复这样的的过程多次,提问每次剩余的是几分之几?
【实验结果】
第一次剪去一半,实物观察剩余1/2;第二次剪去余下的一半,剩余四分之一,即(1/2)2;第三次剪去余下的一半,剩余八分之一,即(1/2)3;第四次剪去余下的一半,剩余十六分之一,即(1/2)4;……
根据实验结果探索规律,教学中首要先让学生思考:从上面实验中你能发现什么规律?让学生经历观察——归纳——提出猜想的过程;接下来鼓励学生推测出“第五次剪去余下的一半,应剩余三十二分之一,即(1/2)5;”然后做做实验,检验猜想的结论是否正确。最后,教师可以根据学生的实际情况,把这个问题进一步推广到一般的情形。第n 次剪去余下的一半,会剩余(1/2)n;当然,应该认识到这个结论的正确性有待进一步证明(归纳证明将在高中学习)。
以上过程实际上是引导学生做实验,经历观察现象——归纳规律——猜想出一般性结论的过程,这正体现了归纳法思想的精髓。将实验二的结论,进一步理论分析,次数n很大时,剩余的(1/2)n会很小很小,趋近于零,但又不为零。此即古人所云“一尺之棰,日取其半,万世不竭”之理。
二、创设情境,培养学生数学归纳的思维能力
数学思维能力的培养是教学的重要任务之一。归纳法作为一种方法性知识,在教学中应着重培养学生的思维能力。笔者认为,在归纳法的教学过程中,可以借用经典例题和数学趣史,创设情境,激发兴趣,开阔眼界,锻炼智力,增长知识,从而培养归纳思维的能力。下面举例说明:
例1:(课程标准102页的例子)
15×15=1×2×100+25=225
25×25=2×3×100+25=625
35×35=3×4×100+25=1225……
教学中可以借用此例,以计算结果和恒等变形为情境,启发引导学生探索规律,培养学生数学归纳法的思维能力。首先让学生思考:从上面这些算式的计算中你能发现什么规律?让学生经历观察、比较、归纳、提出猜想的过程;接下来鼓励学生推测“45×45,55×55 应该是多少,并计算验证猜想的结果”。最后,教师还可以根据学生的实际情况,把这个问题进一步推广到一般的情形:若用字母a代表一个正整数,则应有规律(a×10+5)2=a(a+1)×100+25。但这样的猜想是否正确,需要给出证明:(a×10+5)2=a2×100+2a×10×5+25=a(a+1)×100+25。这是一个由具体数值计算到符号公式表达的过程,即由特殊到一般的过程。这样,学生充分体验了观察——归纳——猜想——证明的思维过程,形成了数学归纳法的思维能力。
三、剖析真题,让学生领悟中考归纳法的应用难度
纵观近五年的中考试题,涉及归纳法应用的考题较多。这与课程标准“教师在教学过程中,应该引导学生通过观察、尝试、归纳、类比、图画等活动发现规律,猜测结论,发展合情推理能力”的要求是一致的。以下通过剖析真题,让学生领悟中考试题的难易程度。
例1:(2014中考)观察下列一组图形中点的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,……
按此规律第5个图中共有点的个数是()
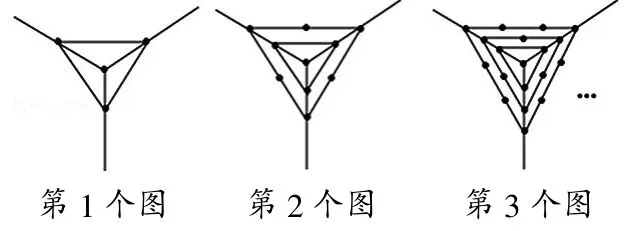
A.31 B.46 C.51 D.66
本题考查学生观察图形,归纳变化规律,猜想结论,合情推理的能力。检测了学生数学归纳法的思维水平,在2014年中考10个选择题中,排在第9,属于较难题。
分析:由图可知:其中第1个图中共有1+1×3=4个点,第2个图中共有1+1×3+2×3=10个点,第3个图中共有1+1×3+2×3+3×3=19个点,…由此规律得出第 n个图有 1+1×3+2×3+3×3+…+3n个点.
解答:
第1个图中共有1+1×3=4个点,
第2个图中共有1+1×3+2×3=10个点,
第 3个图中共有 1+1×3+2×3+3×3=19个点,
…
第 n个图有 1+1×3+2×3+3×3+…+3n个点。
所以第5个图中共有点的个数是1+1×3+2×3+3×3+4×3+5×3=46.
故选:B
数学归纳法作为一种方法性知识,无论从应考的角度还是从培养学生思维能力的角度,都具有重要的意义和研究价值。正如法国数学家拉普拉斯所说:“即使在数学里,发现真理的主要工具也是归纳和类比。”这句话充分体现了归纳法在数学思维中的重要作用。
