自回归法AR模型在篮球进攻技术指标统计中的应用研究*

刘 毅 李秋平 任建立

（湖南中医药高等专科学校公共课部，湖南 株洲 412012）

自回归法AR模型在篮球进攻技术指标统计中的应用研究*

刘 毅1李秋平1任建立1

（湖南中医药高等专科学校公共课部，湖南 株洲 412012）

对NBA2012-2013赛季热火队季后赛的篮球进攻技术指标进行统计和分析，并建立预测模型。研究结果：建立了篮球二分出手次数、二分命中率、三分出手次数、三分命中率、罚球次数、罚球命中率、助攻、进攻篮板和失误等9项篮球进攻技术指标的自回归AR模型（1,1,1）；根据自回归AR模型（1,1,1），建立了9个自回归AR模型方程；运用自回归法AR模型能够对篮球进攻技术指标统计分析做出短期预测，为球队战术制定、人员安排等提供科学依据。

自回归法；AR模型；篮球；进攻；技术指标

20世纪60年代以来，预测的理论和应用得到了迅速的发展，并日趋完善，逐渐成为一门自成体系的学科。在体育领域有对体育成绩、奖牌情况、体育产业等问题的预测研究，本文尝试运用自回归法AR模型对篮球进攻技术指标进行预测研究，通过研究证实自回归法AR模型在篮球进攻技术指标统计分析中的有效性和科学性，并为篮球战术制定、训练计划安排、人员配置等方面提供科学依据。

1 研究对象

NBA2012—2013赛季热火队季后赛23场比赛的篮球进攻技术指标二分出手次数、二分命中率、三分出手次数、三分命中率、罚球次数、罚球命中率、助攻、进攻篮板和失误为研究对象。

2 研究方法

运用自回归法AR模型，利用SPSS19.0软件对比赛整理数据进行统计分析。

3 结果与分析

3.1 自回归法AR模型在篮球进攻技术指标统计中的识别分析过程

3.1.1 自回归法AR模型在二分出手次数、二分命中率序列中的识别分析过程

从2012—2013赛季热火队季后赛二分出手次数、二分命中率指标序列图（该图省略）分析：（1）2012—2013赛季热火队季后赛23场比赛中二分出手次数指标序列具有一定的周期性，且有向上的趋势性，序列前半部分低于后半部分。（2）2012—2013赛季热火队季后赛23场比赛中二分命中率指标序列具有一定的周期性，序列前一阶段高于后一阶段，有向下的趋势线。（3）该序列无离群点和缺失值[3]。

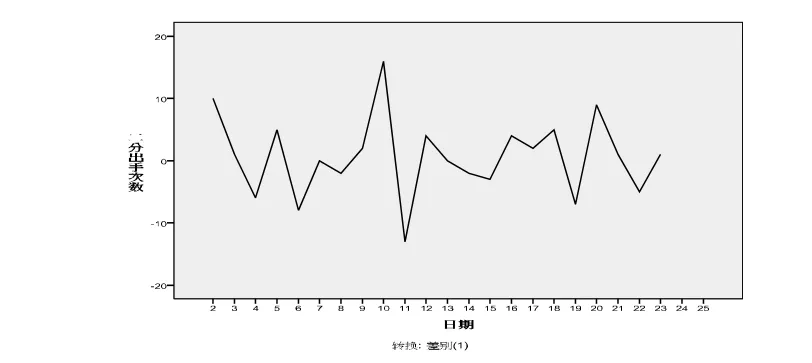
图1 二分出手次数一阶差分后的序列图

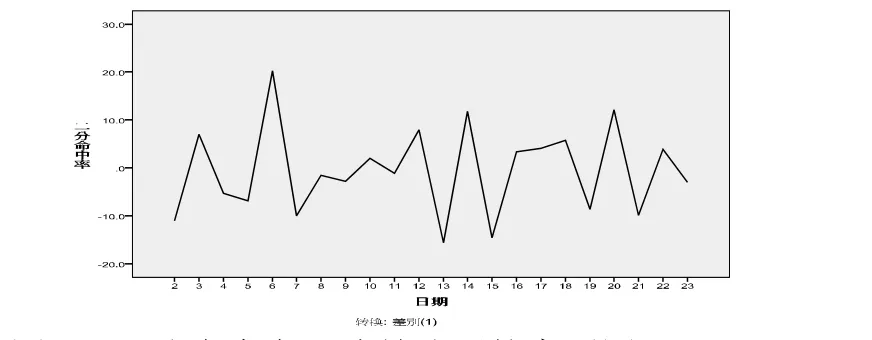
图2 二分命中率一阶差分后的序列图

为了使序列的特征体现得更加明显，利于分析模型的选择，满足于模型的要求，在此对数据进行变换处理，采用差分处理的办法，通过逐项相减消除前后期数据相关性的办法，大致剔除序列中的趋势性，使数据在水平方向基本平稳[1]。根据自回归法的基本思路，在此选择了1阶差分。由图1和图2可知：经过一阶差分后，2012—2013赛季热火队季后赛二分出手次数、二分命中率指标序列的趋势得到了彻底的消除，并且可以看出具有一定周期性。

从2012—2013赛季热火队季后赛二分出手次数指标、二分命中率指标一阶差分的自相关图和偏自相关图（该图省略）可知：经过一阶差分后的第1阶均显著不为0，基本可以判断自相关函数1阶拖尾；偏自相关函数为1截尾。此时可以估计p=1，d=1。

3.1.2 自回归法AR模型在三分出手次数、三分命中率序列中的识别分析过程

从2012—2013赛季热火队季后赛三分出手次数、三分命中率指标序列图（该图省略）分析：2012—2013赛季热火队季后赛23场比赛中三分出手次数、三分命中率序列具有一定的周期性。三分出手次数指标序列在前半段、后半段震荡明显，中间部分序列较为平稳。三分命中率指标序列后半部分高于前半部分，有向上的趋势性。该序列无离群点和缺失值。为了消除序列中的强趋势性，使其他相关因素更加鲜明地体现出来，经过1阶差分处理后，可以确定AR模型中的参数d应为1。从2012—2013赛季热火队季后赛三分出手次数、三分命中率指标序列一阶差分的自相关图和偏自相关图（该图省略）可知：经过一阶差分后的第1阶函数值均显著不为0，基本可以判断自相关函数1阶拖尾；偏自相关函数为1截尾。此时可以估计p=1，d=1。

3.1.3 自回归法AR模型在罚球次数、罚球命中率序列中的识别分析过程

从2012—2013赛季热火队季后赛罚球次数、罚球命中率指标序列图（该图省略）分析：2012—2013赛季热火队季后赛23场比赛中罚球次数存在下降的趋势，罚球命中率序列具有一定的周期性。该序列无离群点和缺失值。经过一阶差分的自相关图和偏自相关图（该图省略）可知：经过一阶差分后的第1阶函数值均显著不为0，基本可以判断自相关函数1阶拖尾；偏自相关函数为1截尾。此时可以估计p=1，d=1。

3.1.4 自回归法AR模型在进攻篮板、助攻、失误序列中的识别分析过程

从2012—2013赛季热火队季后赛进攻篮板、助攻、失误指标序列图（该图省略）分析：热火队比赛中进攻篮板指标的序列是非平稳序列，具有一定的周期性；助攻、失误指标序列具有下降的趋势性，序列前一阶段高于后一阶段。该序列无离群点和缺失值，根据自回归法的基本思路，在此选择了1阶差分。经过一阶差分的自相关图和偏自相关图（该图省略）可知：经过一阶差分后的第1阶函数值均显著不为0，基本可以判断自相关函数1阶拖尾；偏自相关函数为1截尾。此时可以估计p=1，d=1。

3.2 自回归法AR模型在篮球进攻技术指标统计中的估计分析过程

本文在基本确定差分阶数p=1，d=1以后，分别用2种不同的自回归系数建立AR模型，在此没有展开分析每一个模型的信息，只制作了篮球进攻技术指标的各个模型拟合情况效果表1[4]。根据表1所示，二分出手次数指标的自回归模型AR（1,1,1）的拟合效果好于AR（1,1,0），该模型的决定系数为0.761，决定系数高于自回归模型AR（1,1,0），正态化的BIC值为6.594，BIC值越小的模型，拟合效果越好。二分命中率指标的自回归模型AR（1,1,1）的拟合效果优于AR（1,1,0），该模型的决定系数为0.795，决定系数高于自回归模型AR（1,1,0），正态化的BIC值为6.085，BIC值越小的模型，拟合效果越好。三分出手次数指标自回归模型AR（1,1,1）的决定系数为0.727，正态化的BIC值6.477，三分命中率指标的回归模型AR（1,1,1）的决定系数为0.787，正态化的BIC值6.678，三分出手次数指标、三分命中率指标的自回归模型AR（1,1,1）的拟合效果优于AR（1,1,0）。罚球次数指标、罚球命中率指标的自回归模型AR（1,1,1）的决定系数高于AR（1,1,0）的决定系数，拟合效果优于AR（1,1,0）。进攻篮板、助攻、失误指标的自回归模型AR（1,1,1）拟合效果优于AR（1,1,0）。

表1 热火队进攻技术指标各种模型的拟合效果表

从2012—2013赛季热火队季后赛篮球进攻技术指标模型统计量表（该表省略）可知：2012—2013赛季热火队季后赛篮球进攻技术指标AR（1,1,1）模型的拟合效果比较理想。二分出手次数指标模型的决定系数（R方）达到了0.761，说明模型可以解释原序列76.1%的信息，BIC值也较小，Ljung-Box统计量值也是显著的，这些都说明用AR（1,1,1）模型能很好地拟合序列数据。通过观察统计量数值，二分命中率、三分出手次数、三分命中率等其他指标的AR（1,1,1）模型也能够很好拟合序列数据。

从2012—2013赛季热火队季后赛篮球进攻技术指标模型的参数表2[5]可知：二分出手次数模型的参数为0.893，参数是显著的，常数项为0.454，具有显著性差异，Sig＜0.05，由此推断二分出手次数的拟合模型为Xt+0.893Xt-1=0.454+at。二分命中率模型的参数为-0.485，Sig＜0.05，参数是显著的，常数项为-0.728，具有显著性差异，Sig＜0.05，由此推断二分命中率的拟合模型为Xt-0.485Xt-1=-0.728+at。三分出手次数模型的参数为-0.972，Sig＜0.05，参数是显著的，常数项为0.378，具有显著性差异，Sig＜0.05，由此推断三分出手次数的拟合模型为Xt-0.972Xt-1=0.378+at。三分命中率模型的参数为-0.748，Sig＜0.05，参数是显著的，常数项为0.638，具有显著性差异，Sig＜0.05，由此推断三分命中率的拟合模型为Xt-0.748Xt-1=0.638+at。根据表4推断，罚球次数的拟合模型为Xt+0.627Xt-1=-0.358+at。罚球命中率的拟合模型为Xt-0.772Xt-1=0.413+at。助攻的拟合模型为Xt-0.423Xt-1=-0.712+at。进攻篮板的拟合模型为Xt-0.619Xt-1=0.405+at。失误的拟合模型为Xt+0.745Xt-1=-0.423+at。

表2 热火队季后赛篮球进攻技术指标模型参数表

3.3 自回归法AR模型在篮球进攻技术指标统计中的诊断分析过程

从2012—2013赛季热火队季后赛篮球进攻技术指标AR（1,1,1）模型的残差自相关函数和偏自相关函数图进行模型的诊断分析，从二分出手次数AR（1,1,1）模型残差自相关函数和偏自相关函数图3可以看出[6]，残差的自相关和偏自相关函数都是0阶截尾，因而残差是一个不含相关性的白噪声序列，这说明序列的相关性都已经充分拟合。从二分命中率AR（1,1,1）模型残差自相关函数和偏自相关函数图4可以看出[7]，二分命中率序列的拟合效果较好，残差的自相关和偏自相关函数都是0阶截尾。本文根据三分出手次数、三分命中率、罚球次数、罚球命中率、助攻、进攻篮板和失误进攻技术指标AR（1,1,1）模型的残差自相关函数和偏自相关函数图（该图省略），残差的自相关和偏自相关函数都是0阶截尾，序列的相关性已经充分拟合。

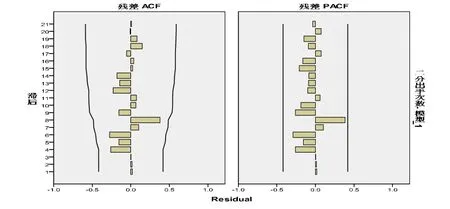
图3 二分出手次数模型残差自相关函数和偏自相关函数图图4二分命中率模型残差图

4 结论

4.1 自回归法AR模型在篮球进攻技术指标统计分析中的结果讨论

（1）本文根据2012—2013赛季热火队季后赛23场比赛的情况，建立了篮球二分出手次数、二分命中率、三分出手次数、三分命中率、罚球次数、罚球命中率、助攻、进攻篮板和失误等9项篮球进攻技术指标的自回归AR模型

（1,1,1）。

（2）二分出手次数指标序列具有一定的周期性，且有向上的趋势性，序列的前半部分低于后半部分；二分命中率指标序列具有一定的周期性，序列的前一阶段高于后一阶段，有向下的趋势线。三分出手次数、三分命中率序列具有一定的周期性。三分出手次数指标序列在前半段、后半段震荡明显，中间部分序列较为平稳。三分命中率指标序列后半部分高于前半部分，有向上的趋势性。罚球次数序列存在下降的趋势，罚球命中率序列具有一定的周期性。进攻篮板指标序列是非平稳序列，具有一定的周期性，助攻、失误指标序列具有下降的趋势性，失误指标序列的前一阶段高于后一阶段。

（3）根据2012—2013赛季热火队季后赛篮球进攻技术指标的自回归AR模型（1,1,1），建立了9个自回归模型方程。二分出手次数的拟合模型为Xt+0.893Xt-1=0.454+at。二分命中率的拟合模型为Xt-0.485Xt-1=-0.728+at。三分出手次数模型的拟合模型为Xt-0.972Xt-1=0.378+at。三分命中率模型的拟合模型为Xt-0.748Xt-1=0.638+at。罚球次数的拟合模型为Xt+0.627Xt-1=-0.358+at。罚球命中率的拟合模型为Xt-0.772Xt-1=0.413+at。助攻的拟合模型为Xt-0.423Xt-1=-0.712+at。进攻篮板的拟合模型为Xt-0.619Xt-1=0.405+at。失误的拟合模型为Xt+0.745Xt-1=-0.423+at。故基于自回归模型可做短期预测。

4.2 自回归法AR模型在篮球进攻技术指标统计分析中的意义

（1）很少有文章运用自回归法AR模型对篮球技术指标进行预测分析的，本文尝试该方法进行模型的识别、估计和诊断，最终确定了预测模型，探索了一种预测篮球比赛技术指标的统计方法。

（2）运用自回归法AR模型能够在篮球进攻技术指标统计分析中做出短期预测，为球队战术制定、训练计划安排和人员安排等提供科学依据。

[1]孙振球，徐勇勇．医学统计学（第三版）[M]．北京：人民卫士出版社，2010．383-400.

[2]薛薇．SPSS统计分析方法及应用[M]．北京：电子工业出版社，2009．403-456.

[3]张小龙．时间序列自回归（AR）模型在体育预测中的应用[J]．北京体育大学学报，2010，33(2)：86-77.

[4]赵聂．时间序列模型在我国年度世界冠军预测中的应用[J]．成都体育学院学报，2008，34(2)：68-72

[5]王国凡，赵武等．基于GA和回归分析的奥运会成绩预测研究[J]．中国体育科技，2011，47(1)：4-10.

[6]杨召，叶中辉等，乘积季节ARIMA模型在结核病发病率预测中应用[J]．中国公共卫生，2013，29(4)：469-472.

[7]陈颇，贾清秀等，ARIMA模型在我国体育用品出口预测中的应用[J]．天津体育学院学报，2007，22(4)：353-357.

the Application of Autoregressive Model in the Statistics of Technical Indicators about Basketball Offensive

LIU Yi，etal.
(Department of Public Lesson, Hunan Traditional Chinese Medicine College,Zhuzhou 412012,Hunan, China)

This paper analyze the technical indicators about basketball offensive of Miami Heat on playoffs in NBA 2012-2013 , and establish the prediction models. According to the results, the article set up the autoregressive models(1,1,1) in the statistics of technical indicators about basketball offensive, such as two or three-point shots field goal attempts, two or three-point shooting, free throw attempts, free throw percentage, assists, offensive rebounds and lapse. The article also builts 9 equations according to the autoregressive models (1,1,1). With the help of the autoregressive method, the AR model obtain a short-term forecasts on counting and analyzing technical indicators about basketball offensive, providing a scientific basis for formulate tactics and staffing, et al.

autoregressive method AR models; Basketball; offensive; technical indicators

2012年度湖南省社科基金研究课题，课题编号：11YBA107。

刘毅（1980-），湖南益阳人，副教授，研究方向：篮球教学训练理论与方法。