旋转运动导电圆板磁弹性振动分析

李 哲，胡宇达，姚臻臻

（1.燕山大学建筑工程与力学学院，河北秦皇岛066004；2.燕山大学河北省重型装备与大型结构力学可靠性重点实验室，河北秦皇岛066004）

旋转运动导电圆板磁弹性振动分析

李 哲，胡宇达∗，姚臻臻

（1.燕山大学建筑工程与力学学院，河北秦皇岛066004；2.燕山大学河北省重型装备与大型结构力学可靠性重点实验室，河北秦皇岛066004）

研究了磁场中旋转运动导电薄板在外激励作用下的强迫振动问题。在给出动能、应变能和电磁能表达式的基础上，根据哈密顿原理导出旋转圆板在磁场中横向载荷作用下的轴对称磁弹性振动方程。假设位移函数并运用分离变量法分离时间变量和空间变量，应用伽辽金积分法，得到激励作用下圆板的强迫振动微分方程并求解。通过数值计算得到简支和固支两种边界条件下的幅频曲线和相轨迹图，分析磁感应强度、圆板的厚度、半径和转速的变化对振动的影响。

磁弹性；旋转圆板；振动；轴对称；伽辽金法

0 引言

在现代高新技术工程领域中，导电导磁类构件在航空航天、核工业、发动机、电磁传感器等装置中有着广泛的应用。处于磁场环境下的导电圆板、圆环板因受到电、力、磁等多场耦合作用，其运动行为较为复杂。目前许多学者对旋转导电圆板研究并取得了一些成果。Bauer H F等［1］研究了不同边界条件下等厚度旋转圆板的振动问题。Touzé C等［2］应用多尺度法计算自由边界圆板的强迫振动问题。Mu T R［3］分析了复合材料圆板的强迫振动问题，运用瑞利⁃里兹法给出了强迫振动的近似解并进行数值分析。Celep Z等［4］对Winkler支撑的刚性圆板强迫振动进行了分析。Xiang Y等［5］针对阶梯圆板在不同边界条件和参数下的自由振动进行了大量研究。Allahverdizadeh A等［6］分析了功能梯度圆板的自由振动和强迫振动。Dong C Y［7］运用切比雪夫⁃里兹法对圆板的电弹性和磁弹性振动进行了研究，并针对不同材料进行了计算和分析。余水丰等［8］针对周期均布载荷作用下轴对称变厚度圆板的非线性强迫振动进行了分析，用小参数摄动法对振动方程进行了求解。胡宇达等［9⁃11］对磁场中的圆形、矩形板的强迫振动及自由振动进行了研究，得到了很多的研究成果。贾乃文等［12］运用分离变量法分析了刚／粘塑型圆板的强迫振动并给出了振动时的挠度与内力解。徐旭等［13］针对厚圆板的轴对称振动进行了研究，求解了厚圆板在固支和简支条件下的对称与反对称的自由振动问题。杜国君等［14］针对阶梯圆板和环板运用修正迭代法对大挠度振动问题进行了研究。王晋莹等［15］推导出了具有初挠度圆板的振动方程并运用伽辽金法和摄动法求解出振动的周期解。本文得到旋转圆板的磁弹性轴对称强迫振动方程并对其求解，针对周边简支和夹支两种边界条件下的圆板，绘制幅频曲线并分析磁感应强度、圆板半径和厚度变化对振动的影响。

1 旋转圆板磁弹性振动方程

1.1 动能与势能

对于在磁场中做旋转运动的圆形薄板，设薄板内任意一点的位移矢量在柱坐标系3个方向的分量为

式中，ur、uθ为薄板的中面位移；w为薄板的横向位移；和为转角位移；r、θ、z分别为径向、环向和法向坐标；t为时间变量。

根据式（1）～（3），通过求导运算，得到旋转运动薄板的速度分量表达式：

旋转运动薄板由弯曲变形引起的形变势能Uε1表达式为

旋转运动薄板的中面应变势能为

式中，Mr、Mθ为弯矩；Mrθ为扭矩；κr、κθ为曲率；κrθ为扭率；Nr、Nθ、Nrθ为中面内力；εr、εθ、γrθ为中面应变。

1.2 哈密顿原理建立振动方程

根据哈密顿原理，在固定时刻t0和t1上积分：

将式（5）～（7）代入式（8）中，并考虑轴对称振动问题，经过变分运算，推得旋转运动圆形薄板的磁弹性轴对称振动方程：

1.3 电磁力表达式

在磁场中做旋转运动的薄板将受到洛仑兹力的作用，薄板单位体积内电磁力表达式为

其中，J＝σ0（e＋V×B）；e为电场强度矢量；V为板内各点速度矢量；σ0为电导率。

对式（11）沿板厚方向积分，忽略电场强度的影响，可得到式（9）和（10）中薄板所受电磁力和力矩的表达式为

2 横向磁场中旋转运动圆板的强迫振动

2.1 圆板轴对称强迫振动微分方程

针对在横向磁场环境中的旋转运动圆板，将对应的动能、弯矩内力、中面内力和电磁力、电磁力矩表达式带入到振动方程（10）中，得到旋转运动薄板关于横向挠度的磁弹性轴对称振动方程：

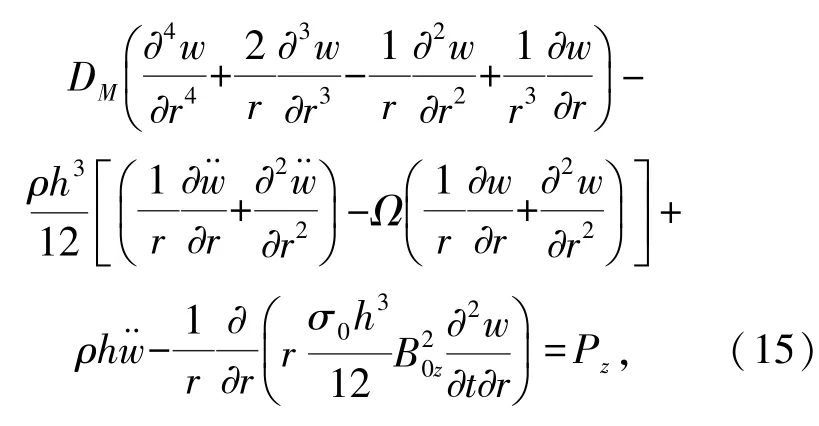
设满足边界条件的位移解为如下展开形式：

其中，R为圆板半径。系数选取为：周边夹支约束情况取 C1＝－2、C2＝1；周边简支约束情况取

将式（16）代入到式（15）中，应用伽辽金法进行积分，得到激励作用下圆板的强迫振动微分方程：

2.2 圆板强迫振动微分方程求解

给定激励力Pz＝q0sin（ωt），q0为激励力幅，ω为激励力频率。则振动微分方程化为

其中，系数b＝b2／b1，无阻尼固有频率＝b1／b4。

振动方程（19）的一个特解为

其中，振幅A＝βqst；放大因子响应与激励的相位差；频率比

3 算例分析

针对铝制圆板磁弹性强迫振动问题计算分析。主要参数：密度ρ＝2 670 kg／m3；半径R＝0.5 m；板厚h＝16 mm；电导率σ0＝3.63×107（Ω·m）－1；泊松比μ＝0.34；弹性模量E＝71 GPa。

图1可以得到在两种边界条件下放大因子随频率比的变化规律：当s＜1时，放大因子呈上升趋势；s＞1时，放大因子呈下降趋势；当s＝1时，系统激励频率接近固有频率，放大因子迅速增大，系统发生共振，由于存在阻尼，最大值在s＝1偏左处；当s＝0时，放大因子β＝1，即激励频率远小于系统固有频率时，系统的响应振幅近似等于系统的静位移；当s→∞时，放大因子β→0，即激励力频率远大于系统固有频率时，振幅趋近于0。当频率比一定时，随着磁感应强度的增加，放大因子随之减小。在相同条件下，简支边界圆板的振幅比固支边界圆板的振幅小。

图2～4可以得到圆板在不同边界条件下，放大因子在不同参数变化时的曲线图。图2可以得出，板厚一定时，放大因子随着转速的增加而减小；转速一定时，随着板厚增加到某一值时，放大因子迅速增加，进入共振区域；随着板厚的继续增加，放大因子迅速减小并趋近于0。图3可以得到，当磁感应强度比较小时，两种边界条件下圆板出现共振区域；当磁感应强度不断增加时共振峰值逐渐减小最后变化平缓。当圆板半径一定时，两种边界条件下放大因子随着磁感应强度的增加而随之减小。图4可以得到在简支边界条件下，放大因子随着圆板转速的增加而减小。在固支边界条件下随着磁感应强度的增加，不同转速的曲线出现交叉点，当磁感应强度取值小于交叉点时，放大因子随着转速的增加而减加；当磁感应强度取值大于交叉点时， 放大因子随着转速的增加而减小。

图1 磁感应强度变化幅频曲线图Fig.1 Curve of amplitude⁃frequency with different magnetic induction intensity

图2 不同边界条件下圆板的放大因子⁃转速⁃板厚图（B0z＝4 T、ω＝200 rad／s）Fig.2 Curve of amplification factor⁃rotation speed⁃plate thickness with different boundary conditions（B0z＝4 T、ω＝200 rad／s）

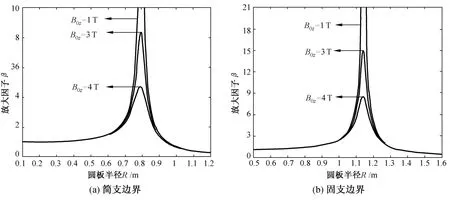
图3 不同磁感应强度下放大因子⁃半径曲线图（n＝9 000 r／min、ω＝200 rad／s）Fig.3 Charactertic curve of amplification factor⁃radius with different magnetic induction intensity（n＝9 000 r／min、ω＝200 rad／s）

图5～7为两种边界条件下的不同参数对应的相轨迹图，可以得到在频率比一定时，两种边界条件下圆板的振幅随着磁感应强度和板厚的增大而减小、随着转速的增加而增加。相同激励时简支边界圆板的振幅比固支边界圆板的振幅大。对于两种边界条件可以看出，板厚的变化对振动影响最大。

图4 不同转速下放大因子⁃磁感应强度特性曲线图（h＝8 mm、ω＝200 rad／s）Fig.4 Charactertic curve of amplification factor⁃magnetic induction intensity with different rotation speed（h＝8 mm、ω＝200 rad／s）

图5 不同磁感应强度下相轨迹图（n＝9 000 r／min、ω＝250 rad／s、h＝10 mm）Fig.5 Phase trajectory with different magnetic induction intensity（n＝9 000 r／min、ω＝250 rad／s、h＝10 mm）

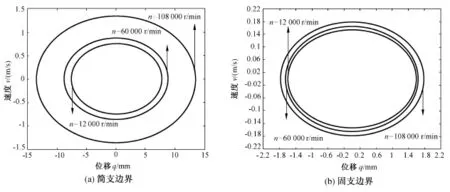
图6 不同转速下相轨迹图（B0z＝4 T、ω＝100 rad／s、h＝100 mm）Fig.6 Phase trajectory with different rotation speed（B0z＝4 T、ω＝100 rad／s、h＝100 mm）

图7 不同板厚的相轨迹图（B0z＝4 T、ω＝100 rad／s、n＝9 000 r／min）Fig.7 Phase trajectory with different plate thickness（B0z＝4 T、ω＝100 rad／s、n＝9 000 r／min）

4 结论

1）导出了旋转运动圆板在横向磁场中的强迫振动方程并对其求解。

2）数值计算结果得到：a）画出幅频曲线图，给出了不同磁感应强度下放大因子与频率比的关系，得到了系统的共振区域；b）给出放大因子与板厚、半径和转速的关系，并得到了在不同转速和半径条件下放大因子与磁感应强度的关系；c）通过相轨迹图给出了振幅与磁感应强度、转速和板厚的关系，其中板厚对系统振动影响最大。

［1］Bauer H F，Eidel W.Transverse vibration and stability of spinning circular plates of constant thickness and different boundary condi⁃tions［J］.Journal of Sound and Vibration，2007，300（3／5）：877⁃895.

［2］Touzé C，Thomas O，Chaigne A.Asymmetric non⁃linear forced vibrations of free⁃edge circular plates.part1：theory［J］.Journal of Sound and Vibration，2002，258（4）：649⁃676.

［3］Mu T R.Forced vibration of the two⁃layer piezoceramic and metal composite thin circular plate with different diameter for each layer［J］.Chinese Journal of Acoustics，1983，2（3）：229⁃243.

［4］Celep Z，Genço lu M.Forced vibrations of a rigid circular plate on a tensionless Winkler edge support［J］.Journal of Sound and Vibra⁃tion，2003，263（4）：945⁃953.

［5］Xiang Y，Zhang L.Free vibration analysis of stepped circular Mindlin plates［J］.Journal of Sound and Vibration，2005，280（3／5）：633⁃655.

［6］Allahverdizadeh A，Naei M H，Bahrami M N.Nonlinear free and forced vibration analysis of thin circular functionally graded plates［J］.Journal of Sound and Vibration，2008，310（4／5）：966⁃984.

［7］Dong C Y.Vibration of electro⁃elastic versus magneto⁃elastic circu⁃lar／annular plates using the Chebyshev⁃Ritz method［J］.Journal of Sound and Vibration，2008，317（1／2）：219⁃235.

［8］余水丰，夏永旭.变厚度圆板的非线性强迫振动［J］.上海力学，1992，13（3）：59⁃66.

［9］胡宇达，杜国君.磁场环境下导电圆形薄板的磁弹性强迫振动［J］.工程力学，2007，24（7）：184⁃188.

［10］胡宇达，孙建涛.磁场中轴向运动导电薄板的强迫振动分析［J］.应用力学学报，2013，30（3）：339⁃343.

［11］胡宇达，徐耀玲，白象忠.横向磁场中圆板的轴对称振动［J］.振动与冲击，1998，17（4）：71⁃74.

［12］贾乃文，余华昌.刚／粘塑性圆板的强迫振动［J］.振动与冲击，1999，18（2）：65⁃68.

［13］徐旭，何福保.厚圆板轴对称振动的弹性力学解［J］.力学季刊，2000，21（1）：59⁃65.

［14］杜国君，胡宇达.阶梯圆形和环形薄板的大幅度基本振动［J］.应用力学学报，1998，15（1）：71⁃78.

［15］王晋莹，陈科进.具有初挠度的柔韧圆板的振动问题［J］.应用数学和力学，1993，14（2）：165⁃171.

Forced oscillation of conductive rotating circular plate in magnetic field

LI Zhe1，2，HU Yu⁃da1，2，YAO Zhen⁃zhen1，2
（1.School of Civil Engineering and Mechanics，Yanshan University，Qinhuangdao，Hebei 066004，China；2.Key Laboratory of Mechanical Reliability for Heavy Equipments and Large Structures of Hebei Province，Yanshan University，Qinhuangdao，Hebei 066004，China）

Forced oscillation of a conductive rotation thin circular plate under external excitation in magnetic field is investigated.By using Hamilton principle，the magneto⁃elastic vibration equations of a conductive rotating thin circular plate are deduced under the ac⁃tion of transverse load with the expressions of kinetic energy and strain energy considered.According to the set of a displacement func⁃tion and the separation of time and spatial variables with the method of separation of variables，forced oscillation differential equation with the load is obtained and solved through the application of Galerkin integral method.The amplitude⁃frequency and phase trajectory curves are obtained with fixed and simply supported boundary condition through the numerical calculation，the stability.The influence of magnetic induction intensity，rotation speed，plate thickness and radius on the vibration of the spinning plate are analyzed finally. Key words：magneto⁃elastic；forced oscillation；round plate；axial symmetry；Galerkin integral method

O442；O327

A

10．3969／j．issn．1007⁃791X．2015．05．014

1007⁃791X（2015）05⁃0464⁃07

2015⁃07⁃07 基金项目：国家自然科学基金资助项目（11472239）；河北省自然科学基金资助项目（A2015203023）；河北省高等学校科学技术研究重点项目（ZD20131055）

李哲（1990⁃），男，黑龙江铁力人，博士研究生，主要研究方向为磁弹性动力学；∗通信作者：胡宇达（1968⁃），男，黑龙江牡丹江人，博士，教授，博士生导师，主要研究方向为非线性振动、磁弹性力学等，Email：huyuda03＠163.com。