基于电流注入法的光伏电源并网谐波电压畸变分析

石磊磊，韩天华，唐 超，卫 丹，赵凡凡，贾清泉，∗

（1.国网河北省电力公司邢台供电分公司，河北邢台054001；2.燕山大学电气工程学院，河北秦皇岛066004）

基于电流注入法的光伏电源并网谐波电压畸变分析

石磊磊1，2，韩天华1，唐 超1，卫 丹1，赵凡凡2，贾清泉2，∗

（1.国网河北省电力公司邢台供电分公司，河北邢台054001；2.燕山大学电气工程学院，河北秦皇岛066004）

通过研究光伏并网对电网电压畸变的影响机理，本文提出了基于电流注入法的电网谐波电压畸变分析方法。建立了光伏并网系统的谐波源模型，将光伏电源等效为谐波电流注入源，推导出光伏谐波注入源与配电网各点谐波电压畸变率的关系式，得出光伏电源接入位置和有功出力对电网谐波电压的影响关系。对含多个光伏电源接入的配电网谐波分布特性和相互影响关系进行了理论分析与仿真，得出光伏电源接入后的谐波分布规律，并验证了本文方法的正确性。

光伏发电；电能质量；谐波畸变；电流注入法

0 引言

近年来，随着国家对光伏发电重视程度和政策支持力度的加大，光伏并网发电的规模越来越大。2015年3月，国家能源局下发《关于下达2015年光伏发电建设实施方案的通知》，2015年全国将新增光伏电站建设规模为17.8 GW。光伏电源大多通过逆变器接入配电网，由于电力电子设备的非线性，接入配电网会产生谐波问题。当多个光伏电源并网时，不同光伏逆变器会带来谐波交互影响［1］，进一步提高了光伏发电系统注入电网的谐波含量，严重影响电网的供电质量［2⁃3］。因此分析光伏电源的并网位置和输出功率对电网谐波的影响具有重要理论和实际意义。

国内外学者针对光伏电源接入配电网产生的电能质量问题开展了一定的研究。文献［4］利用解耦潮流算法对含分布式电源的配电网进行了谐波分析，表明分布式电源接入配电网会注入大量的谐波电流，增加系统的谐波畸变水平。文献［5⁃6］分析了分布式电源不同接入技术对电网谐波分布的影响。文献［7］利用MATLAB／Simulink对分布式电源产生的谐波在电网中的传播机理进行了分析，表明分布式电源接入电网的电气距离越远，高次谐波电流越小。文献［8⁃10］讨论了光伏并网逆变器的输出谐波模型。

本文建立了光伏并网系统的谐波源模型和接入光伏电源的配电网等效模型，将光伏电源等效为谐波电流注入源，通过理论推导得出光伏电源不同接入位置和有功出力与电网谐波电压的关系式。对含光伏电源的配电网进行理论和仿真分析，得出各节点各次谐波电压畸变率和相互影响规律，验证了本文分析方法的正确性。

1 光伏并网系统谐波源建模

光伏发电系统主要的谐波来源是电力电子逆变器，其输出的谐波含量取决于自身特性和工作条件，因此可以将其看成内阻很大的电流源。光伏并网逆变器的谐波特性可以用式（1）来表示。

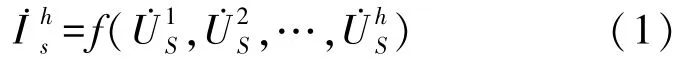
本文采用电流注入法，即假定由某些谐波电流源注入节点的各次谐波电流幅值和相角，都仅仅与流过该电流源的基波电流的幅值和相角成线性关系。由此可以得出谐波电流源接入配电网的谐波分布规律。

光伏电源并入配电网如图1所示。假设电网中三相负荷平衡，忽略线路集肤效应和分布电容。光伏电源在距离B母线a处接入，设L为B母线到负荷的距离，U0为B母线端电压，Ug为光伏电源接入点的电压，U为输电线路末端电压。

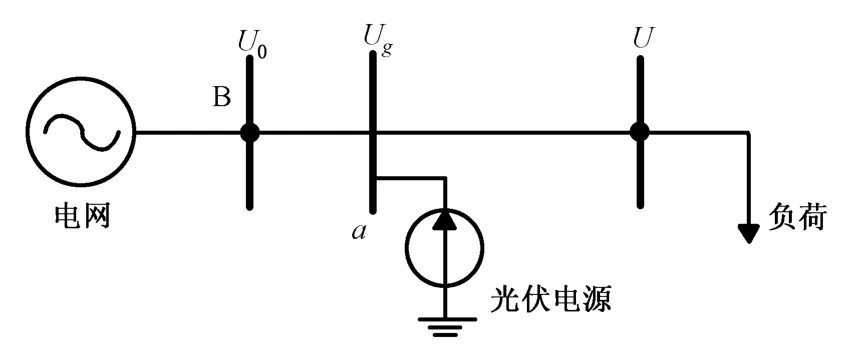
图1 接入光伏电源的配电网模型Fig.1 The distribution network with photovoltaic connected

光伏电源并网的谐波网络模型如图2所示。输电线路第h次谐波的单位长度阻抗为r＋jhx，光伏电源和负荷谐波源向电网注入的谐波用电流源gh和h表示，其幅值与基波电流幅值呈线性关系，线性系数分别为kgh和kh，如式（2）、（3）所示：

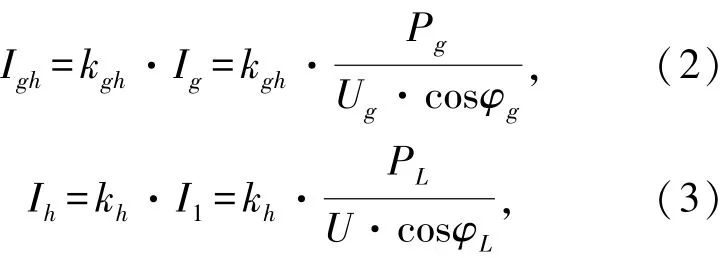
式中，Pg和cosφg分别为光伏电源输出的有功功率和功率因数，PL和cosφL分别为负荷的有功功率和功率因数。

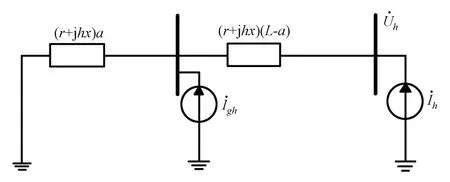
图2 接入光伏电源配电网谐波模型Fig.2 Harmonic model of the distribution network with photovoltaic connected

2 光伏电源接入配电网谐波畸变率分析

2.1 光伏电源接入容量对线路谐波电压的影响

图1中，光伏电源未接入时，距离B母线a处 h次谐波电压幅值为

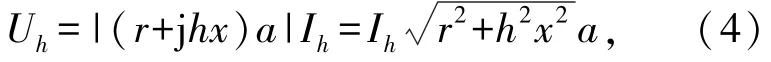
接入光伏电源后，第h次（h≥2）谐波电压幅值为

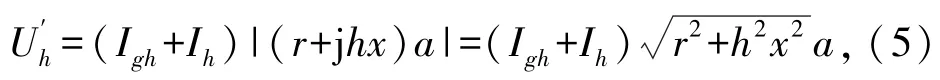
光伏电源接入后谐波电压的变化量ΔUh为

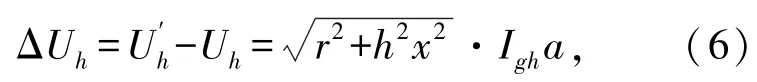
将式（6）代入式（3）可得

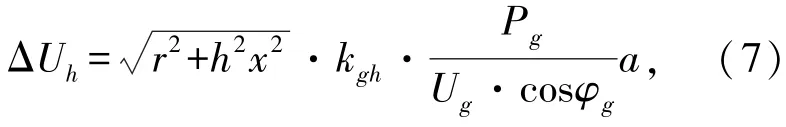
由式（7）可知，谐波电压变化量受光伏电源容量与接入位置的影响。在光伏接入位置不变情况下，如果光伏电源接入容量Pg增大，由式（7）可知，谐波电压增大，且增加量ΔUh与Pg成正比关系。

2.2 光伏电源接入位置对谐波电压的影响

1）光伏电源接入点上游线路的谐波电压

光伏电源接入点上游线路距离B母线L（L＜a）处的h次谐波电压为

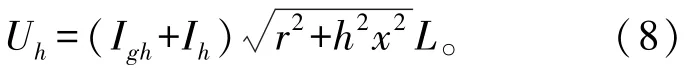
在光伏电源接入容量Pg和负荷PL不变情况下，由式（2）和式（3）可知，谐波电流Igh和Ih也不变。根据式（8），随着L增大，光伏电源接入点上游线路谐波电压也随之增大。

2）光伏电源接入点下游线路的谐波电压

光伏电源接入点下游线路距离B母线a处的h次谐波电压为

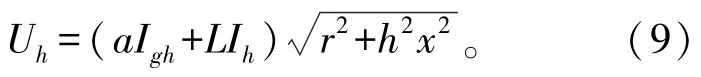
由式（9）可知，对于光伏电源接入点下游线路，随着L增大，谐波电压也随之增大。

当多个光伏电源共同接入配电网时，谐波电压的变化量为光伏电源单独接入时产生谐波电压的叠加，第k个节点处h次谐波电压为

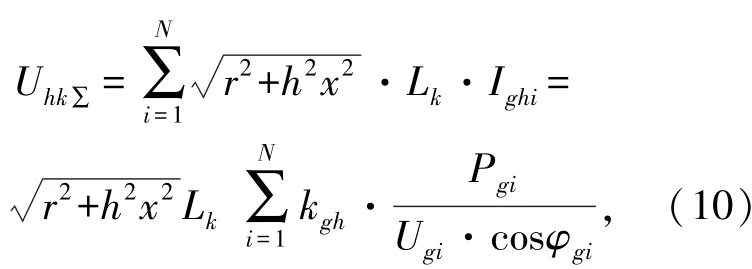
式中，ai为第i个光伏电源接入点与B母线之间的距离，N为配电网接入光伏电源的数量。

2.3 配电网接入光伏电源后电压谐波畸变率的计算方法

本文中光伏电源接入配电网后各节点电压谐波畸变率的计算方法如下：

1）将某时刻配电网各节点光伏电源接入容量（未接入光伏的节点，其光伏电源容量为0）、功率因数、线路节点间长度、单位长度电阻、单位长度电抗等参数代入式（10）求出节点k的谐波电压。

2）根据式（11）计算各节点电压谐波畸变率：

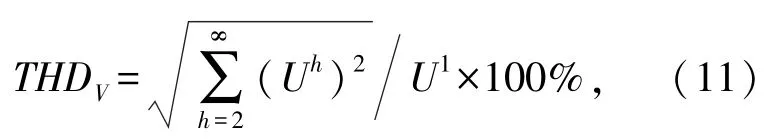
式中，Uh为第h次谐波电压，U1为基波电压。

3）根据步骤（2）的结果，判断分布式光伏电源接入后电网各节点的谐波畸变率是否满足国家标准的要求，进行汇总可得电压谐波畸变率越限的节点。

3 算例分析

算例选取某实际配电网的一条出线，沿馈线将每一个集中负荷视为一个节点，电网母线端编号为1，依次编号，构成一条10节点的网络，如图3所示。根据2.3节所述方法计算各节点电压畸变率的理论值，并将其与MATLAB／Simulink仿真得到的结果进行比较。

3.1 光伏电源接入不同节点时谐波电压畸变率分析

1）接入光伏电源前后各节点谐波电压畸变率对比

在图3中的节点2加入容量为30 kW的光伏电源，计算光伏电源接入前后，各节点的电压畸变率如图4所示。从图中可知，电压畸变率变化量ΔTHDV随着光伏电源接入配电网距离的增加而增大。光伏电源接入前的谐波电压畸变率远小于光伏电源接入后的谐波电压畸变率，说明光伏电源接入配电网后，极大地增加了谐波电压畸变率，成为配电网中重要的谐波污染源。图4中各节点谐波电压畸变率理论计算值与仿真值之间最大相对误差约为4.2%，主要原因是本文方法忽略了电网谐波与光伏电源注入谐波之间的相互作用，因此造成理论值与仿真值之间的误差，但可以满足光伏电源接入配电网电压谐波畸变率评估计算的需要。

2）单个光伏电源接入不同节点时谐波电压畸变率

在图3中4、10节点处依次加入有功功率为30 kW的单一光伏电源，仿真得到馈线各节点的谐波电压畸变率THDV曲线如图5所示。

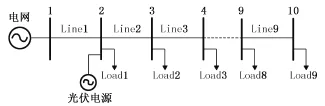
图3 含光伏电源的配电网结构图Fig.3 Structure of distribution network with photovoltaic power connected

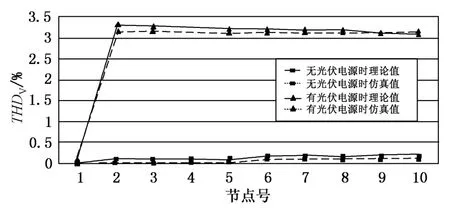
图4 加入光伏电源前后谐波电压畸变率Fig.4 Harmonic voltage distortion rate before and after the connection of photovoltaic power

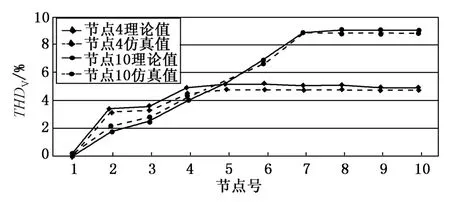
图5 单个光伏电源接入不同节点时谐波电压畸变率Fig.5 The THDVof single photovoltaic power connected with different nodes

如图5所示，相同容量光伏电源接入电网的不同位置，各节点的谐波电压畸变率差别较大。光伏电源接入点上游各节点，谐波电压畸变率较小；光伏电源接入点下游各节点，谐波电压畸变率较大，其中某些节点的谐波电压畸变率可能会超过《电能质量 公用电网谐波》（GB／T 14549—93）规定的限值。图5中各节点谐波电压畸变率理论值与仿真值最大相对误差约为4.6%。

3）多个光伏电源接入时谐波电压畸变率

在图3中节点4和10同时接入两个有功出力均为30 kW的光伏电源，与单独接入时得到各次谐波的电压畸变率进行对比。图6和图7分别为节点2各次谐波畸变率的理论值和仿真值，图8和图9分别为节点4各次谐波畸变率的理论值和仿真值。由于实际光伏电源输出的偶次谐波和19次以上的奇次谐波含量很少，因此这些谐波忽略不计。

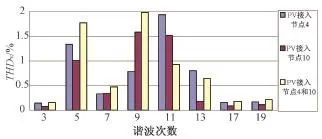
图6 节点4各次谐波THDV理论值Fig.6 THDVtheoretical value of node 4

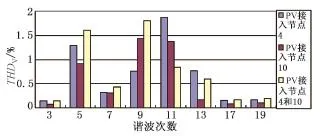
图7 节点4各次谐波THDV仿真值Fig.7 THDVsimulation value of node 4

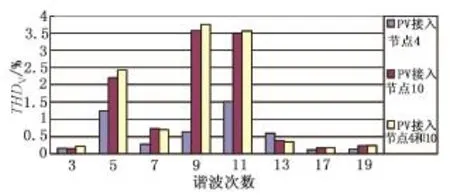
图8 节点10各次谐波THDV理论值Fig.8 THDVtheoretical value of node 10

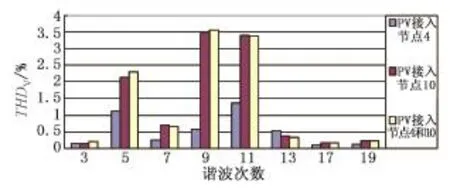
图9 节点10各次谐波THDV仿真值Fig.9 THDVsimulation value of node 10

光伏电源并网后产生的谐波在传播过程中以5次、9次和11次谐波为主。当两个光伏电源同时接入配电网时，二者产生的各次谐波会互相作用，5次、9次和11次等低次谐波变化较明显。通过对比可以发现，各次谐波电压畸变率理论计算值与仿真值最大相对误差约为4.5%。

3.2 光伏电源输出不同有功时谐波电压畸变率分析

配电网接入负荷总量为80 kW，在节点3处分别接入有功功率为50 kW和90 kW的光伏电源，仿真得到谐波电压畸变率THDV曲线如图10所示。从图中可以看出，当光伏电源接入电网的位置不变时，光伏电源输出有功功率为90 kW时（超过了配电网接入负荷总量），谐波电压畸变率THDV较高，有些节点（节点3～10）会超出国家标准规定的限值。通过比较可知，理论计算值与仿真值最大相对误差约为4.8%。

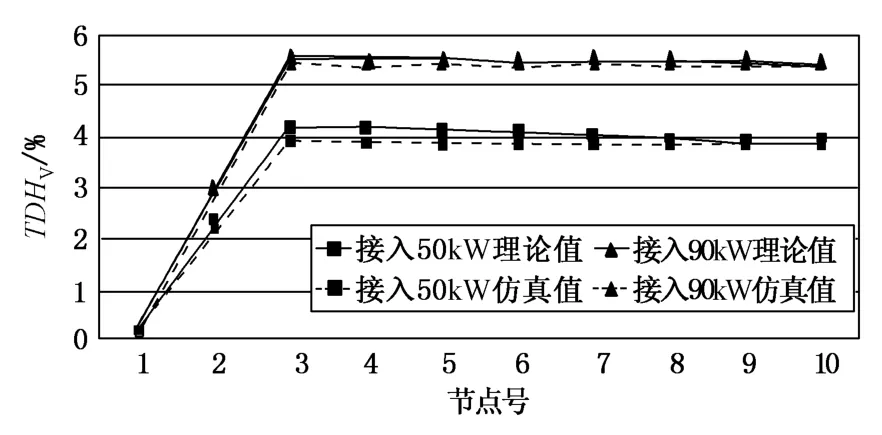
图10 光伏电源输出不同有功时谐波电压畸变率Fig.10 THDVof different photovoltaic active power output

4 结论

本文运用电流注入法建立了光伏电源接入配电网的谐波电压畸变率分析方法，得出光伏电源接入位置和有功出力对电网谐波电压影响关系的计算式。对某配电网接入光伏电源前后配电网中谐波电压畸变率变化情况进行了理论分析和仿真。理论计算和仿真结果之间误差较小，验证了所提出方法的有效性。本文的主要结论如下：

1）有功出力相同的光伏电源接入配电网的位置越接近配电网末端，接入点下游馈线各节点的电压畸变越严重。反之，越接近配电网首端，造成的谐波影响越小。因此，光伏电源不适合接入配电网馈线末端。

2）光伏电源接入配电网位置固定时，馈线各负荷节点上的谐波电压畸变率由光伏电源的有功出力决定，有功出力越大，馈线各负荷节点电压谐波畸变率就越大，畸变率增加量与光伏电源的有功出力成正比，当光伏电源有功出力超过负荷时会超过国家标准允许的限值。

［1］宣文华，牛益国，谢小英，等.基于频域分析和低通滤波的光伏并网逆变器谐振抑制研究［J］.燕山大学学报，2015，39（4）：347⁃351.

［2］丁明，王伟胜，王秀丽，等.大规模光伏发电对电力系统影响综述［J］.中国电机工程学报，2014，34（1）：1⁃14.

［3］赵争鸣，雷一，贺凡波，等.大容量并网光伏电站技术综述［J］.电力系统自动化，2011，35（12）：101⁃107.

［4］Ladjavardi M，Masoum M A S，Islam S.Impact of a SG nonliner model on the harmonic distortion of a distribution generation system［C］／／2008 Australasian Universities Power Engineering Conference，Sydney，Australia，2008：226⁃231.

［5］钟清，高新华，余南华，等.谐波约束下的主动配电网分布式电源准入容量与接入方式［J］.电力系统自动化，2014，38（24）：108⁃113.

［6］Fortes M Z，Ferreira V H，Machado I S，et al.Harmonic analysis of distributed generation in smart city Búzios project［C］／／2015 IEEE Workshop on Power Electronics and Power Quality Applica⁃tions（PEPQA），Bogotá，Colombia，2015：1⁃5.

［7］谢秉鑫，王宗，范士林.分布式电源对于配电网谐波特性的影响［J］.电力系统保护与控制，2012，40（2）：116⁃119.

［8］许得志，汪飞，毛华龙，等.多并网逆变器与电网的谐波交互建模与分析［J］.中国电机工程学报，2013，33（12）：64⁃71.

［9］谢宁，罗安，陈燕生，等.大型光伏电站动态建模及谐波特性分析［J］.中国电机工程学报，2013，33（36）：10⁃17.

［10］胡伟，孙建军，马谦，等.多个并网逆变器间的交互影响分析［J］.电网技术，2014，38（9）：2511⁃2518.

Harmonic distortion analysis of grid⁃connected photovoltaic source based on current injection method

SHI Lei⁃lei1，2，HAN Tian⁃hua1，TANG Chao1，WEI Dan1，ZHAO Fan⁃fan2，JIA Qing⁃quan2
（1.Xingtai Power Supply Company，State Grid Hebei Electric Power Company，Xingtai，Hebei 054001，China；2.School of Electrical Engineering，Yanshan University，Qinhuangdao，Hebei 066004，China）

The voltage distortion influence mechanism of photovoltaic grid⁃connected system is studied in this paper.The harmonic voltage distortion analysis method is presented based on the current injection method.The harmonic source model of the photovoltaic grid⁃connected system which is equivalent to the harmonic current injection source is established.The relation formula of the photo⁃voltaic harmonic injection sources and voltage distortion rate of each node of the distribution network is obtained.The relationship between the interconnected location of photovoltaic source and the active power output to the harmonic voltage of the power network is also obtained.The harmonic distribution characteristics and interaction relationship are studied when multiple photovoltaic sources are connected to distribution network，and the harmonic distribution law is also obtained.The correctness of the method presented in this paper is verified by comparing theoretical analysis with simulation results.

photovoltaic generation；power quality；harmonic distortion；current injection method

TM46

A

10．3969／j．issn．1007⁃791X．2015．05．010

1007⁃791X（2015）05⁃0443⁃05

2015⁃08⁃10 基金项目：国家自然科学基金资助项目（51477147）

石磊磊（1985⁃），男，河北邯郸人，博士研究生，工程师，主要研究方向为分布式光伏并网及其电能质量问题；∗通信作者：贾清泉（1970⁃），男，吉林白山人，博士，教授，博士生导师，主要研究方向为电能质量、新能源电力系统，Email：jiaqingquan＠sina.com。