含双馈异步风电机组的配电网无功优化

潘 峰，夏泽超

（太原科技大学电子信息工程学院，山西太原030024）

含双馈异步风电机组的配电网无功优化

潘 峰∗，夏泽超

（太原科技大学电子信息工程学院，山西太原030024）

针对双馈异步风电机组的出力具有随机性这一特点，采用场景分析法对其出力进行分析，使其更有代表性；在此基础上，建立了以电压偏差最小和有功功率损耗最小的多目标无功优化模型；针对粒子群算法存在易早熟的问题，提出了一种自适应混沌粒子群算法（ACPSO），并将其作为无功优化的算法；利用该算法对含双馈异步风电机组的IEEE33系统进行无功优化计算，并将优化后的结果与其它文献提出的算法相比较，验证了所提算法的有效性。

配电网；双馈异步风电机组；无功优化；自适应混沌粒子群算法；场景分析法

0 引言

近年来，双馈异步风电机组作为分布式电源被广泛接入配电网中，但是风能具有随机性［1］，使并网前系统的无功优化方案不再适用于并网后的系统上，因此，有必要对含双馈异步风电机组配电网的无功优化进行研究。

传统的配电网无功调节手段通常包括调节有载调压变压器的档位和电容器的组数，这种调节手段具有离散化、速度慢的特点［2］。为此，本文基于双馈异步风电机组连续可调的无功发生能力，将其参与配电网的无功优化。配电网的无功优化是一个多变量、多约束条件的非线性规划问题，目前研究的算法主要有免疫算法［3］、粒子群算法［2，5⁃7］和禁忌搜索算法［8］等。其中，粒子群算法因具有易处理离散变量、收敛速度快等优点被广泛应用到无功优化中，但粒子群算法搜索存在盲目性和滞后性以及粒子的早熟收敛等问题［4］，因此，许多学者对粒子群算法加以了改进。文献［2］利用波函数描述粒子的状态，提高了全局搜索能力，但局部搜索能力较差。文献［5］通过加入了混沌扰动来提高算法的多样性，但忽视了惯性权重和学习因子在寻优中的作用。文献［6］对惯性权重和学习因子均进行了改进，但不能有效克服算法易“早熟”的问题。文献［7］提出一种将粒子群算法和遗传算法混合的优化算法，但收敛速度较慢。

本文提出一种自适应混沌粒子群算法，该算法对惯性权重和学习因子采用自适应调整策略，来提高全局和局部的寻优能力；加入了自适应混沌扰动策略，用于克服早熟收敛的发生。最后将改进后的算法应用到无功优化中进行验证。

1 双馈异步风电机组的场景分析

由于双馈异步风电机组的出力具有随机性，导致并网后系统的无功优化问题也具有随机性。因此，为了克服这种随机性，本文将采取场景分析法［9］加以解决。首先，双馈异步风电机组的出力与风速的关系为

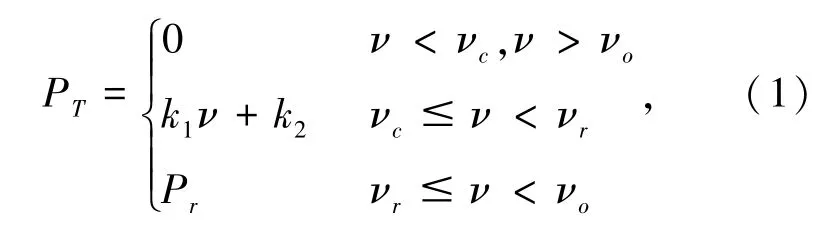
式中，νc、νr、νo和Pr分别是双馈异步风电机组的切入风速、额定风速、切出风速和额定功率，

根据式（1）可以将双馈异步风电机组的出力分成场景1、场景2和场景3。其次，风速分布可近似于Weibull分布［8］，其分布函数为

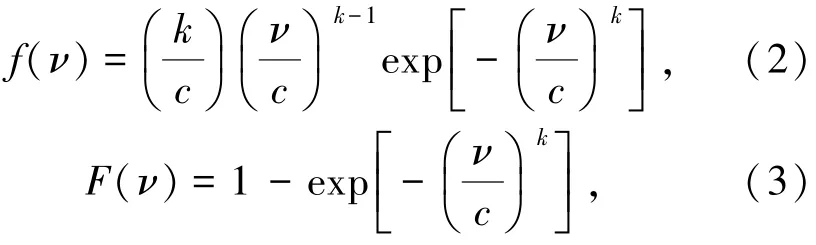
式中，k是形状参数，c是尺度参数，f（ν）是概率密度函数，F（ν）是分布函数。

利用式（3）可以求出 3个场景概率 p1、p2、p3为

根据式（1）可知，场景1的场景功率P1为0，场景3的场景功率P3为Pr。由于场景2的场景功率随风速变化而变化，因此取期望功率更具代表性，即

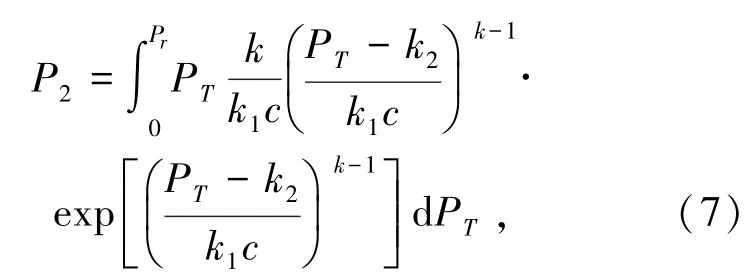
利用式（4）～（7）可以求出双馈异步风电机组的期望功率Pe为

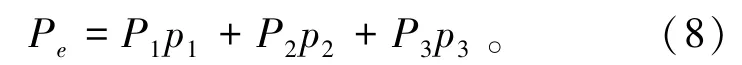
在此基础上，双馈异步风电机组还要满足［2］

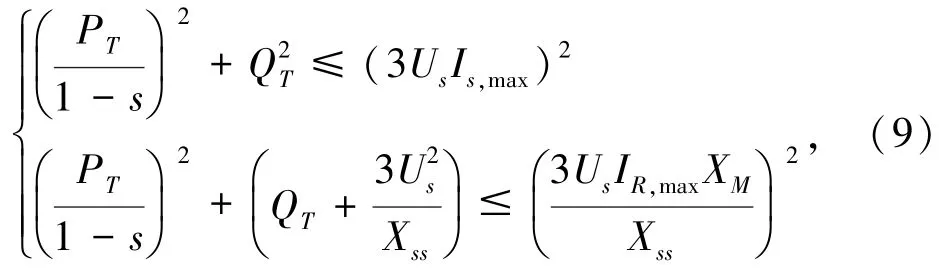
式中，s是转差率，Is，max是定子侧最大电流，IR，max是转子侧最大电流，Xss是定子漏抗与励磁电抗之和，XM是励磁电抗，Us是定子侧电压，PT和QT是风电机组的有功出力和无功出力。

2 无功优化的数学模型

2.1 目标函数

本文综合考虑配电网的安全性和经济性，将配电网的有功损耗和电压偏移量最小作为目标函数，即

式中，n为配电网的支路数，m为配电网的节点数，Pl和Ql为支路l末端的有功功率和无功功率，Ui为节点i的实际电压，UN为节点i的额定电压，ΔUi，max为节点i的最大电压偏差。

由于有功损耗和电压偏差不能直接相加，所以先将其转化成无单位的式子，即

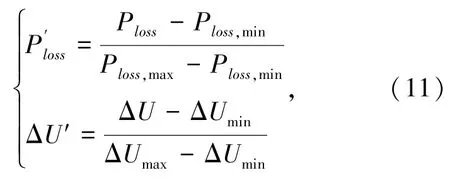
式中，Ploss，max和ΔUmax为初始状态下的有功损耗和电压偏差值，Ploss，min和ΔUmin为有功损耗和电压偏差的理想值。

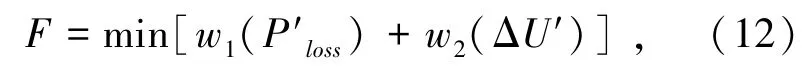
式中，w1和w2分别为0～1之间的权重系数，该系数反映了对于配电网优化运行时的经济性和安全性的偏好程度，同时要求满足w1＋w2＝1。本文在以配电网运行的有功损耗为主要优化目标的基础上，同时还兼顾配电网运行时的电压偏差，因此将w1和w2设定为0.8和0.2。

2.2 变量约束条件

控制变量包括双馈异步风电机组的无功出力Q、有载调压变压器的档位n1、电容器的投切组数n2。状态变量为节点电压U。这些变量要满足相应的约束条件，即

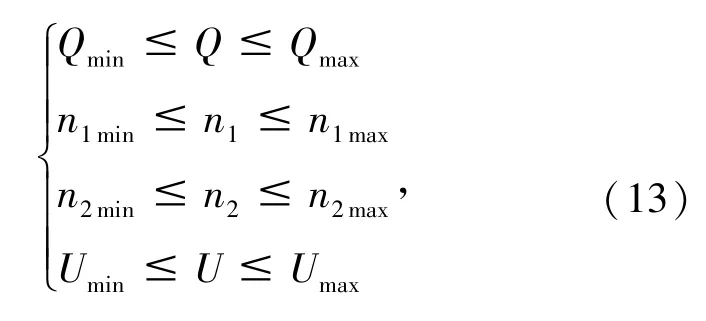
式中，下标“min”和“max”分别代表相应变量的下限和上限。

2.3 功率约束条件

在优化模型中，要确保任意节点注入有功功率和无功功率的平衡，即

式中，Pi和Qi分别为节点i注入的有功功率和无功功率，Gij和Bij以及θij分别为节点i和节点j之间的电导、电纳和电压相角差。

3 ACPSO算法在无功优化中的应用

3.1 ACPSO算法

粒子群算法是一种基于群体智能的启发式全局优化技术［10］，在利用粒子群算法进行无功优化时，算法容易出现早熟收敛现象，该现象导致算法的寻优停滞在一个局部范围内，使得优化效果不理想。因此，本文从3个方面对粒子群算法进行改进，将改进后的算法称为ACPSO算法。

1）对适应度较差的粒子赋予较大的惯性权重，使其跳出适应度较差的区域；对于适应度值较优的粒子赋予较小的惯性权重，使其在适应度较好的区域继续寻优。惯性权重的调节公式为

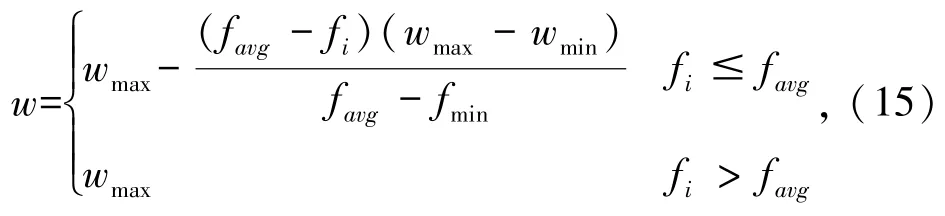
式中，wmax和wmin分布是惯性权重的最大值和最小值，favg是当前种群的平均适应度值，fmin是当前种群的最小适应度值。

2）在算法初期赋予较大的自我学习因子和较小的社会学习因子，以提高初期的全局寻优能力；在后期赋予较小的自我学习因子和较大的社会学习因子，以提高后期的局部寻优能力。学习因子的调节公式为

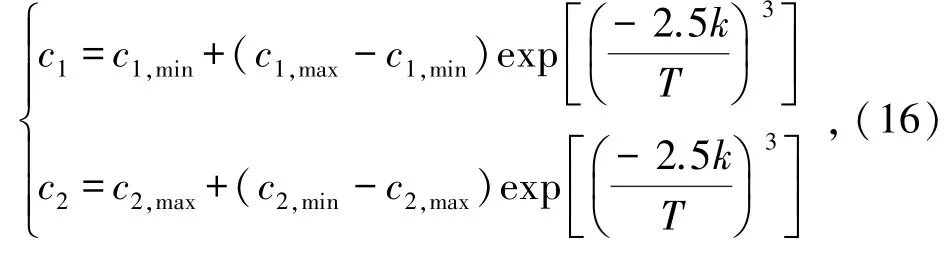
式中，下标“min”和“max”分别学习因子的下限和上限，k为当前代数，T为迭代次数。

3）为提高算法在寻优过程中的多样性，本文将利用混沌的遍历性和内在规律性［11］，在算法出现早熟收敛时，对当前的最优个体进行混沌扰动。其中，利用群体适应度方差作为是否出现早熟收敛的标准，群体适应度方差的计算公式为［12］

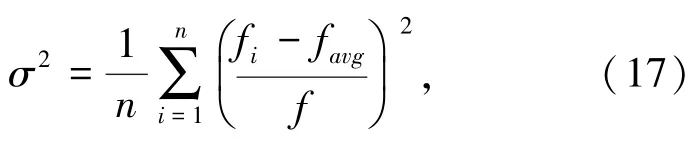
式中，σ2为群体适应度方差，n为粒子个数，fi为第i个粒子的适应度，favg是当前群体平均适应度，f＝max［1，max｜fi－favg｜］。

由式（17）看出，当σ2值越小，种群的多样性越小。因此设定一个阈值，如果群体适应度方差小于这个阈值，就对最优个体进行混沌扰动。混沌扰动的步骤：1）用式（18）将当前种群的全局最优解xgbest映射到0～1内；2）用式（19）对z0进行N次迭代计算，产生一组混沌序列zm（m＝1，2，…，N）；3）用式（20）将混沌序列映射到原来的解空间，产生一组可行解；4）对这组可行解进行适应度计算，选其中适应度最佳的解代替当前种群中的任意一个粒子，并更新此时的全局最优解。

式中，xmin和xmax为全局最优解的下限和上限。

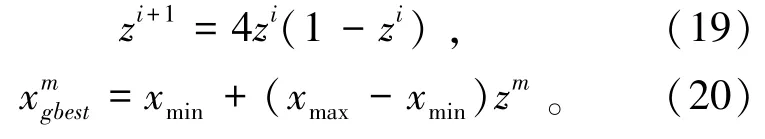
3.2 基于ACPSO算法的无功优化

1）输入配电网参数、ACPSO算法参数和双馈异步风电机组参数。

2）在控制变量的约束范围内，随机生成初始化种群。

3）对初始化种群进行潮流计算，并确定个体最优解和全局最优解。

4）利用式（15）和（16）计算惯性权重和学习因子，并更新粒子速度和位置。

5）对当前种群进行潮流计算，并确定个体最优解和全局最优解。

6）利用式（17）判断种群是否出现早熟收敛：出现时对全局最优值进行混沌扰动；没出现时直接进入7）。

7）判断是否达到最大迭代次数：达到时输出优化结果；没达时返回4）。

4 算例分析

选IEEE33节点配电系统作为算例，配电网的参数见文献［13］，双馈异步风电机组的参数见文献［14］。首节点放置含9个档位的有载调压变压器，步进量为1.25%；在节点6、15、29处分别安装了7组可投切电容器，每组的容量为100 kvar；在33节点处安装了容量1.5 MW的双馈异步风电机组，该双馈异步风电机组的切入风速、额定风速、切出风速分别为3 m／s、13.5 m／s、20 m／s，形状参数和尺度参数分别为2.0和8.5；配电网的电压额定范围是0.93～1.07 p.u。

利用双馈异步风电机组的参数可以算出，场景1、2、3的场景概率分别为 0.121 1、0.802 6、0.076 3，场景1、2、3的场景功率分别为0、0.75、1.5 MW，根据式（8）～（9）得出双馈异步风电机组的期望功率是0.716 4 MW，此时的无功极限是－0.966 2 Mvar～0.842 4 Mvar。

ACPSO算法参数设置：种群规模N为50；迭代次数T为100；惯性权重w为0.4～0.9；学习因子c为0.5～2.5。为验证ACPSO算法的有效性，利用ACPSO算法与文献［5］的CPSO算法、文献［6］的WCSPSO算法分别对上述算例进行无功优化。其中，CPSO算法和 WCPSO算法的参数设置与ACPSO算法相同。

表1中T为有载调压变压器的档位，C1、C2和C3分别是节点15、29和6的电容器投切组数，Q为双馈异步风电机组的无功出力，综合目标函数值是经过对有功损耗和电压偏差做加权处理之后的值。从表1中发现，初始状态下的配电网综合目标函数值很大，利用3个算法进行无功优化后，配电网的综合目标函数值有大幅度下降，其中，利用ACPSO算法优化后，综合目标函数值下降的最多，说明加入自适应混沌扰动能够有效克服早熟收敛的问题，从而收敛精度较高。从图1中发现，本文算法迭代28次就很接近最优解，而其他两个算法均在40代之后才接近最优解，说明加入自适应惯性权重和学习因子后，算法全局和局部的寻优能力得到提高，从而收敛速度较快。

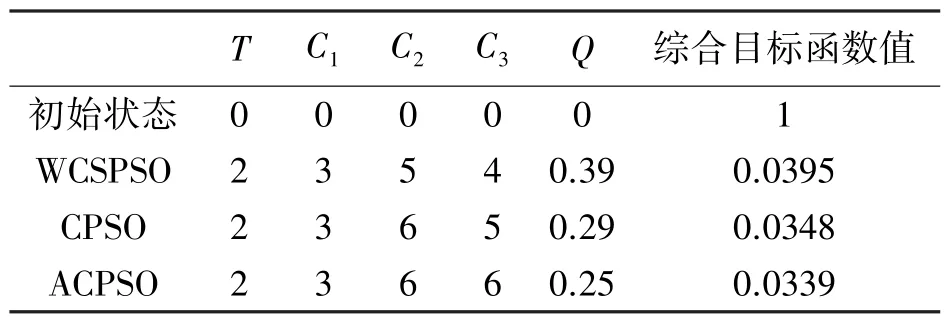
表1 优化前后结果的比较Tab.1 Comparison of results before and after optimization

从图2中发现，利用ACPSO算法对配电网进行无功优化后，不但配电网节点电压均在0.93～1.07 p.u内，同时从整体上看基本接近额定电压1 p.u，说明ACPSO算法可以有效提高配电网的电能质量。

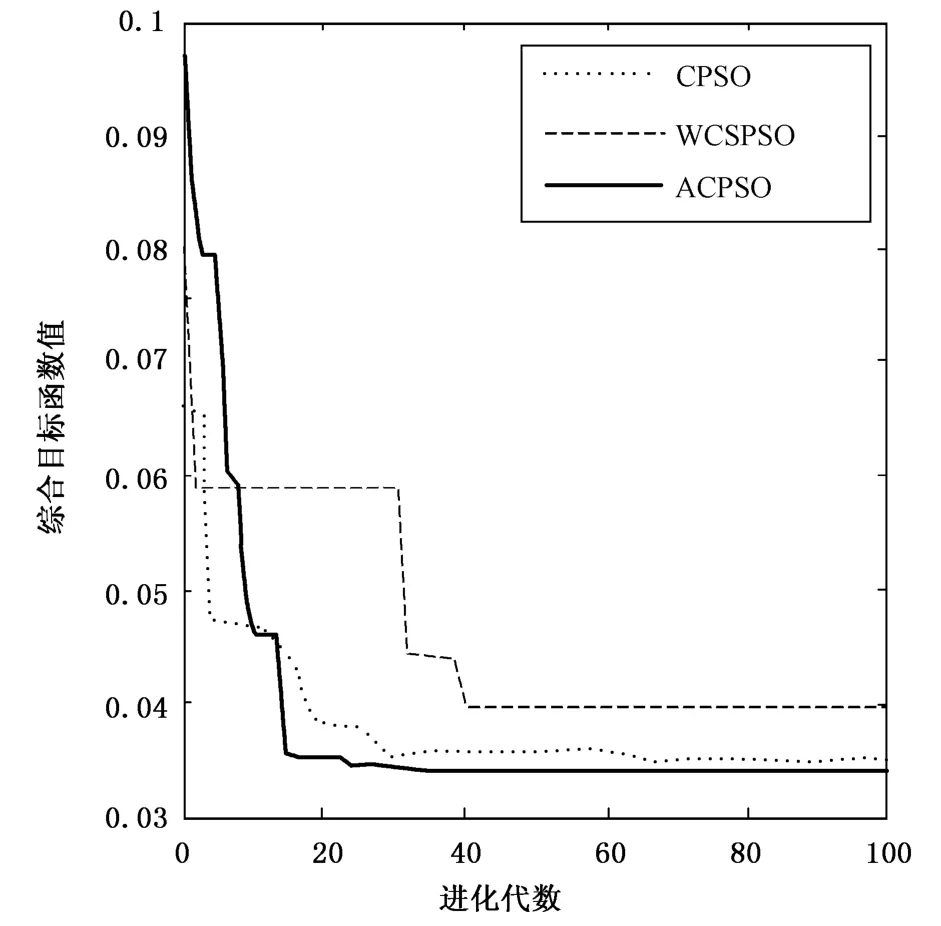
图1 3种优化算法的收敛曲线比较Fig.1 Comparison of the convergence curves of the three kinds of optimization algorithms

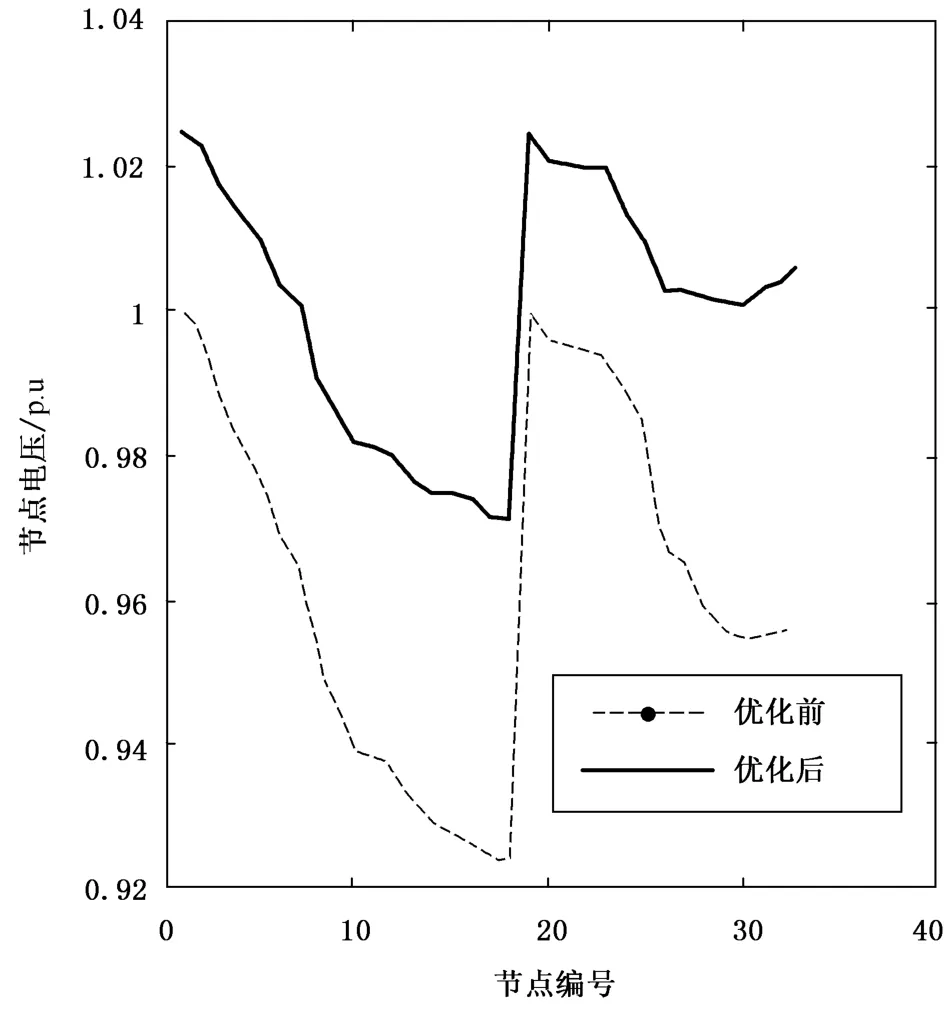
图2 优化前后节点电压的比较Fig.2 Comparison of node voltage before and after optimization

5 结术语

本文利用双馈异步风电机组的无功输出能力，提出了基于ACPSO算法的含双馈异步风电机组配电网无功优化的方法，并将优化结果与其他两种算法进行比较。结果发现，不论收敛精度还是收敛速度均优于其他两种算法，进而验证了ACPSO算法在无功优化领域的可行性。

［1］赵晶晶，符杨，李东东.考虑双馈电机风电场无功调节能力的配电网无功优化［J］.电力系统自动化，2011，35（11）：33⁃38.

［2］李闯，陈民铀，付昂，等.含风电场的配电网无功优化策略研究［J］.电力系统保护与控制，2013，41（9）：100⁃105.

［3］张丽，徐玉琴，王增平，等.包含分布式电源的配电网无功优化［J］.电工技术学报，2011，26（3）：168⁃174.

［4］李鑫滨，马阳，鹿鹭.一种基于校正因子的自适应简化粒子群优化算法［J］.燕山大学学报，2013，37（5）：453⁃458.

［5］吴璇，王建.基于多目标混沌粒子群算法的矿区电网无功优化［J］.低压电器，2011（20）：40⁃42.

［6］雷敏，杨万里，彭晓波，等.基于改进简化粒子群算法的含DG的配电网无功优化［J］.华北电力大学学报，2015，42（1）：39⁃44.

［7］杨洪，陆金桂.基于遗传算法和粒子群算法优化算法的电力系统无功优化［J］.南京工业大学学报，2007，29（5）：58⁃61.

［8］余健明，刘飞.基于禁忌搜索算法的含风电机组的配电网无功优化研究［J］.西安理工大学学报，2013，29（1）：70⁃75.

［9］何属清，鹏建春，毛丽林，等.含多个风电机组的配电网无功优化［J］.电力系统自动化，2010，34（19）：37⁃41.

［10］李鑫滨，朱庆军，马红霞，等.粒子群算法及其在电力系统无功优化中的应用［J］.燕山大学学报，2008，32（3）：245⁃250.

［11］唐贤伦，张衡，周家林，等.多Agent结构的混沌PSO在无功优化中的应用［J］.电机与控制学报，2013，17（6）：15⁃21.

［12］赵志刚，常成.自适应混沌粒子群优化算法［J］.计算机工程，2011，37（15）：128⁃130.

［13］Shan Cheng，Min Youchen.Multi⁃objective reactive power optimi⁃zation strategy fordistribution system with penetration of distributed generation［J］.International Journal of Electrical Power and Energy Systems，2014，62：221⁃228.

［14］张永勤.双馈感应电机风电场并网后的配电网无功优化算法［J］.自动化应用，2013，24（7）：74⁃76.

Reactive power optimization of power distribution network with doubly fed induction generator

PAN Feng，XIA Ze⁃chao
（College of Electronic and Information Engineering，Taiyuan University of Science and Technology，Taiyuan，Shanxi 030024，China）

In order to solve the problem that the output of the doubly fed induction generator is stochastic，the method of scene analysis is used to analyze its output，which makes it more representative.Based on the above，a multi⁃objective reactive power op⁃timization model with minimum voltage deviation and minimum active power loss is established.Aiming at the problem that the PSO algorithm is easy to be premature，an adaptive chaos particle swarm optimization（ACPSO）algorithm is proposed，which is used as a reactive power optimization algorithm.Using this algorithm，the reactive power optimization of the IEEE33 system with doubly fed induction generator is calculated，and the optimized results are compared with other algorithms，the effectiveness of the proposed al⁃gorithm is verified.

distribution network；doubly fed induction wind turbine；reactive power optimization；adaptive chaotic particle swarm op⁃timization algorithm；scene analysis method

TM715

A

10．3969／j．issn．1007⁃791X．2015．05．009

1007⁃791X（2015）05⁃0438⁃05

2015⁃05⁃29

∗潘峰（1974⁃），男，山西文水人，副教授，主要研究方向为电力电子、智能控制等，Email：85933014＠qq.com。