不确定非线性系统SISO的综合终端滑模跟踪控制器及扩展状态观测器

钟晓珠，马跃超，刘金宪，邢海龙，王知力

（1.河北科技学院公共课部，河北保定071000；2.燕山大学理学院，河北秦皇岛066004；3.青岛农业大学信息与科学学院，山东青岛266109）

不确定非线性系统SISO的综合终端滑模跟踪控制器及扩展状态观测器

钟晓珠1，马跃超2，∗，刘金宪1，邢海龙3，王知力1

（1.河北科技学院公共课部，河北保定071000；2.燕山大学理学院，河北秦皇岛066004；3.青岛农业大学信息与科学学院，山东青岛266109）

对带有线性动力学性能和非线性动力学性能及带有系统内部不确定因素和外界扰动因素的单输入单输出系统，本文给出了终端滑模跟踪控制方法。由于该系统状态难以测量，本文将系统内部未知的复杂非线性动力学因素及系统外界扰动因素统称为“总扰动”，并视其为系统模型的增广状态。该增广状态及系统状态可以通过一个线性扩展状态观测器同步评估出来。本方法的特点是设计这样一个观测器以保证近似误差一致最终有界于一个半径为设计参数的函数的球内，该球半径可以通过优化设计参数达到任意小的程度。基于所设计的线性扩展状态观测器的输出，文中给出了保证系统输出密切跟踪所需信号的终端滑模控制器，数值模拟的结果表明所给出的控制器是有效的。

滑模控制；扩展状态观测器；非线性系统；一致最终有界

0 引言

在过去的几十年里，各种不确定非线性系统鲁棒控制技术已得到快速发展。在这些鲁棒控制方法中，滑模控制（SMC）技术对于具有内部不确定性及外界扰动性的系统具有良好的鲁棒性［1⁃7］。由于强劲的鲁棒性，SMC技术被广泛用来改进很多实际系统的性能，例如谐波振荡器［8］、倒立摆系统［9］、双罐系统［10］等。近年来，由于终端滑模跟踪控制方法可在有限时间内使系统状态达到平衡，从而吸引了众多学者的关注。文献［11］对单输入单输出（SISO）非线性系统，将快速终端动力学技术用于改进滑模控制性能。文献［12］研究了多输入多输出（MIMO）线性系统的终端滑模控制（TSMC）方法。文献［13］对于不确定多输入线性系统提出了带终端滑模的变结构控制设计方法。应用TSMC方法，文献［14］研究了带时滞的非线性系统的输出调节方法。

然而，通常只有当系统的所有线性及非线性动力学性能已知的情况下，基本的滑模控制律才是可实现的。由于在实际中某些线性及非线性系统动力学性能通常是未知的，因而基本滑模控制难以直接应用到具有未知函数性能的非线性系统上。有鉴于此，近些年，对于非线性不确定系统，人们研究了综合各种不同评估技术的SMC方法。该综合控制方法应用某些评估技术以逼近系统未知动力学性能，逼近模型内部的不确定性能及模型外界扰动因素，基于这些估值则可设计出系统的SMC律。扰动观测器（DO）及模糊逻辑系统常被用做评估手段。对于具有扰动影响的非线性系统，文献［1 5］研究了基于控制的扰动观测器（DOBC）及TSMC。文献［16］提出了基于扰动观测器的一类不确定非线性系统的滑模控制方法，利用模糊逻辑系统逼近未知系统函数。文献［17］对一类具不确定性因素及外界扰动因素的SISO非线性系统，给出了一种自适应模糊滑模控制器，该控制器融合了一个鲁棒积分控制律。然而，这些方法都要求系统状态是可观测的。当多变量系统状态无法观测时，研究不确定非线性系统的SMC问题就变得更具挑战性。

众所周知，扩展状态观测器具有很多良好的性质，诸如只要求系统模型很少的信息量，并能紧密跟踪系统的外界扰动影响及系统状态信息［18⁃23］。本文针对SISO非线性系统，研究了结合线性扩展状态观测器（LESO）的终端滑模跟踪控制方法。该系统模型具有已知的线性动力学性能、未知的非线性动力学性能以及模型内部的不确定因素和外界扰动影响因素，并且系统状态难以测量。所有这些因素被视为系统的“总扰动”，而本文方法主要特点是设计一个LESO用来评估系统“总扰动”及系统状态。对“总扰动”的评估值用以反馈补偿系统，以达到系统扰动的衰减与消除，从而将原系统转化为一个线性系统。因而应用TSMC律设计生成一个线性系统以保证系统输出紧密跟踪所需信号。

1 问题的导出

考虑下述SISO非线性不确定系统

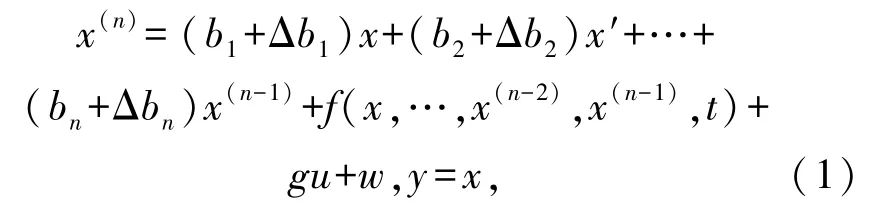
此处，b1，b2，…，bn及 g是已知实常数，u∈R及y∈R分别是输入及输出。未知函数f（·）表示复杂非线性动力学性质，函数Δb1，Δb2，…，Δbn－1及Δbn是模型的不确定性质，函数w是未知的外界扰动。记

W（t）＝Δb1x＋Δb2x′＋…＋Δbnx（n－1）＋f（·）＋w， W（t）被视为系统（1）的总扰动。对系统（1）引入下述假设。

假设：未知函数 w是连续可微的，记W·＝h。所有u，W，h及系统（1）的解是有界的，对于t≥0有｜h｜≤ρ，ρ是已知常数。

方程（1）用状态空间形式改写为

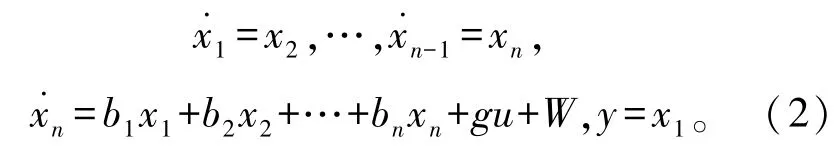
假设系统状态是难以测量的，假定非线性系统（2）是可控的，输入u是有界的，输入增益g是非零的，因此不失一般性设g＞0。控制目的是设计终端滑模控制器，使得系统输出y紧密跟踪当前模型不确定性和外部扰动所生成的信号yd。

为了设计SISO不确定非线性系统（1）的终端滑模控制器，引入下述引理。

引理1［12］假设存在一个连续正定函数V（t）使得：V·（t）＋αV（t）＋λVγ（t）≤0对于∀t＞0，则V（t）在有限时间内收敛于平衡点

2 LESO设计及收敛性分析

令xn＋1（t）＝W（t）是（2）的扩展状态，相应的扩展系统（2）如下：

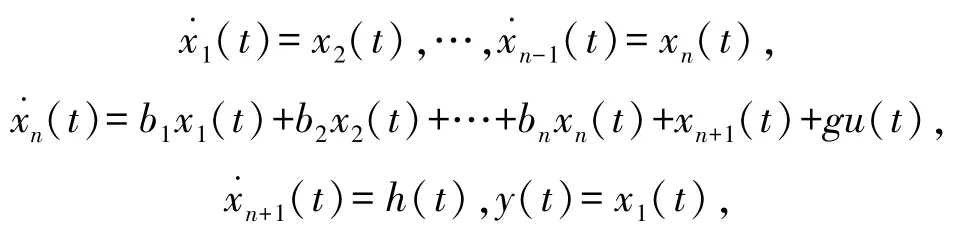
此处x＝（x1x2… xn＋1）T∈Rn＋1表示扩展系统状态向量。上述扩展系统矩阵形式如下：

系统（3）的LESO如下：

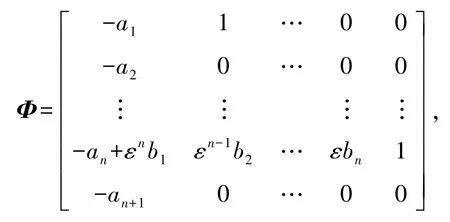
增益参数a1，a2，…，an，an＋1及ε要满足

其中，P及Q是对称正定矩阵。

注1此处LESO（4）的参数矩阵不同于文献［21］中的矩阵。此外选择总扰动

作为扩展状态，即xn＋1（t）＝W（t）。所以该扩展状态并不包含已知线性动力学性能项b1x＋b2x′＋…＋bnx（n－1）。这一跟踪技术完全不同于文献［21］及［22］中给出的典型的ESO方法。引入观测误差Z＝（z1z2… zn＋1）T，其中，zi＝xi－i，i＝1，2，…，n＋1。由（3）减去（4）得到误差动力学系统如下：

定理1考虑满足假设（1）的系统（6）的误差，方程（6）的解Z：［t0t1］➝Rn＋1，Z（t0）＝Z0是一致最终有界的，其最终上界是 κ（ε）＝即对任何0＜ε＜1，有｜｜Z｜｜≤κ（ε），∀t≥tf（ε），此处

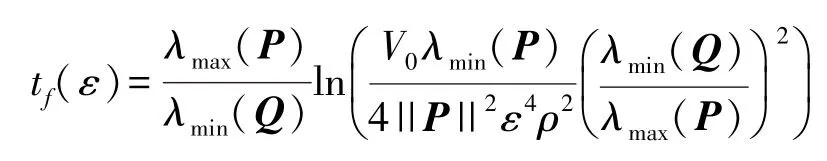
是带有正常数v0的有限时间，v0与ε无关，与初始值有关。

由此，所有的ηi，i＝1，…，n＋1满足下述所有微分方程

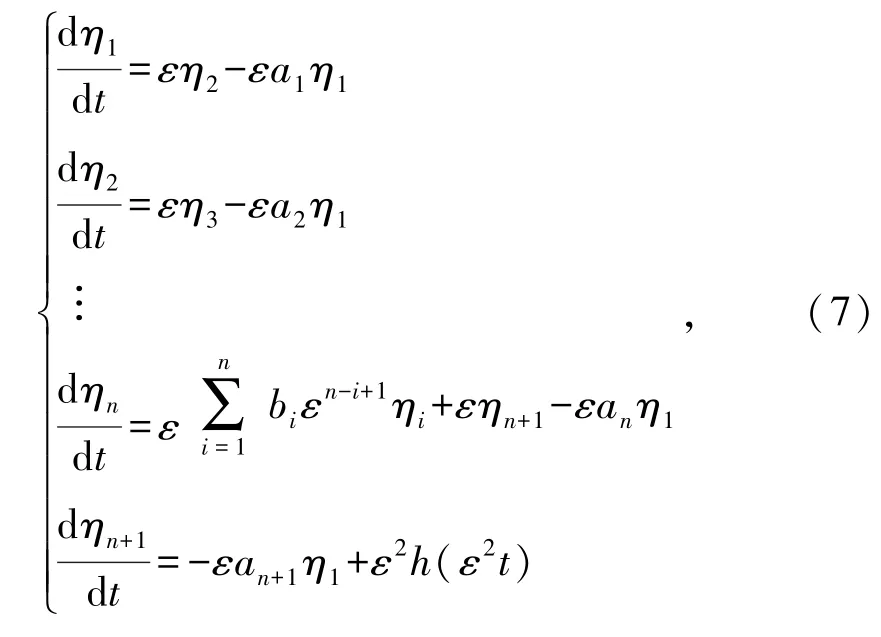
另一方面，如果V0≤ϕ2，则V≤ϕ2（t≥t0），从而存在一个有限时间函数tf（ε）使得对于t≥t0＋ tf（ε），V≤ϕ2并且有。结合ϕ的定义，对于t≥t0＋tf（ε），有

进而，对于t≥t0＋tf（ε）有

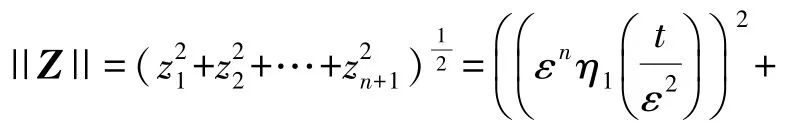
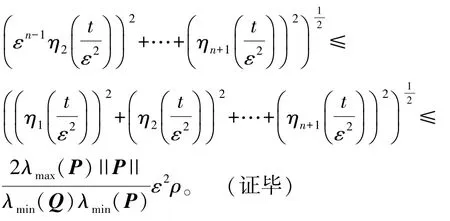
注2由定理1在有限时间tf（ε）后，误差估计进入到闭球｛Z：｜｜Z｜｜≤κ（ε）｝。易证上述闭球的半径可以由设计参数ε调节，而且因为0，当ε➝0误差估计值Z➝0，应当指出所提出的ESO方法是适用于具有已知线性及非线性动力学性能项的扩展状态。

所以LESO（4）既可以对系统状态进行评估，又可以对系统扩展状态进行评估，即

3 终端SMC设计

这里对于所有适于应用LESO方法的系统状态及总扰动给出终端SMC方法。为了得到终端滑模跟踪控制，定义s1＝y－yd，则s1对时间的n阶导数为。由上式，对系统（1）的TSMC方法进行的迭代如下［11］

这里αi＞0，βi＞0，pi及qi，（i＝1，2，…，n－1）是正的奇数并且pi＜qi，对于每一个si，i＝2，…，n－1，有

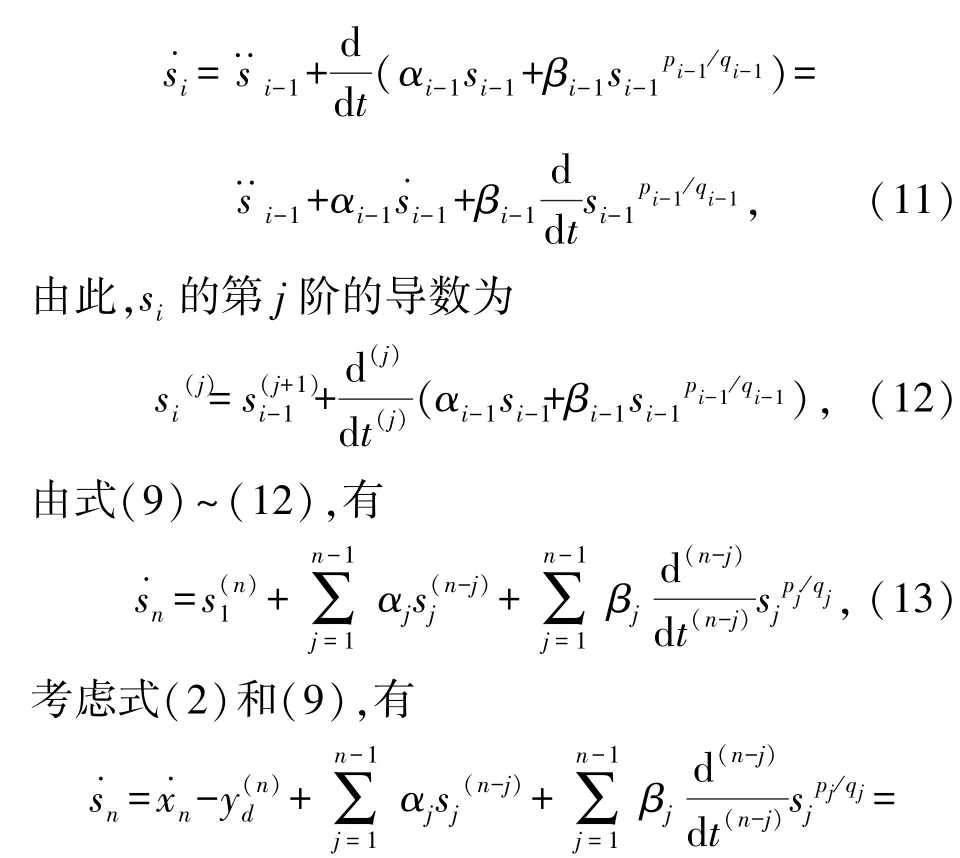
由此，基于终端滑模跟踪控制方法的LESO可以设计为u＝－u0／g，

上述终端滑模控制设计方法可以总结为下述定理。

定理2 考虑具有模型不确定性及外界扰动的不确定非线性系统（1）及LESO被设计为（4）～（5）的形式在终端滑模跟踪控制模型（15）中系统输出y在有限时间内收敛于所需信号yd。

证明把（15）代入（14）得

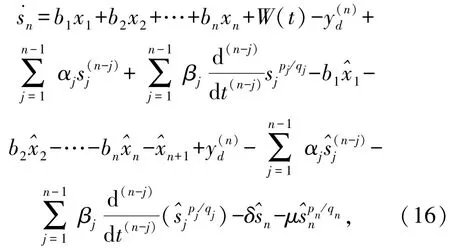
根据引理1及（17）可以知道s1＝y－yd➝0即y➝yd。（证毕）

4 数值模拟

给定的数值模拟的结果说明了本文所提出的控制方法的有效性。考虑一个二阶系统模型：

系统（18）的状态空间形式为

这里模型的不确定性参数为Δb1＝0.02sin（πt），Δb2＝0.02cos（πt），系统非线性动力学函数，外界扰动参数 w（t）＝2sin（0.1πt）＋3sin，所以总扰动参数为

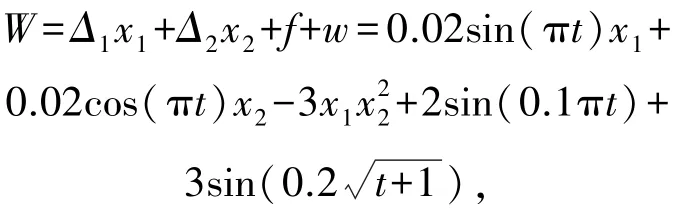
为了设计LESO及滑模控制，增益参数分别取做：ε＝0．01，a1＝2．825 2，a2＝4．408 5，a3＝0．912 9，α1＝50，β1＝0．5，δ＝60，μ＝0．8，p1＝5，q1＝7，初始状态条件任意选择为x1＝0．1，x2＝0．2，预定轨迹取作yd＝2sin（0.2t）。LESO及滑模跟踪控制方法如下给定

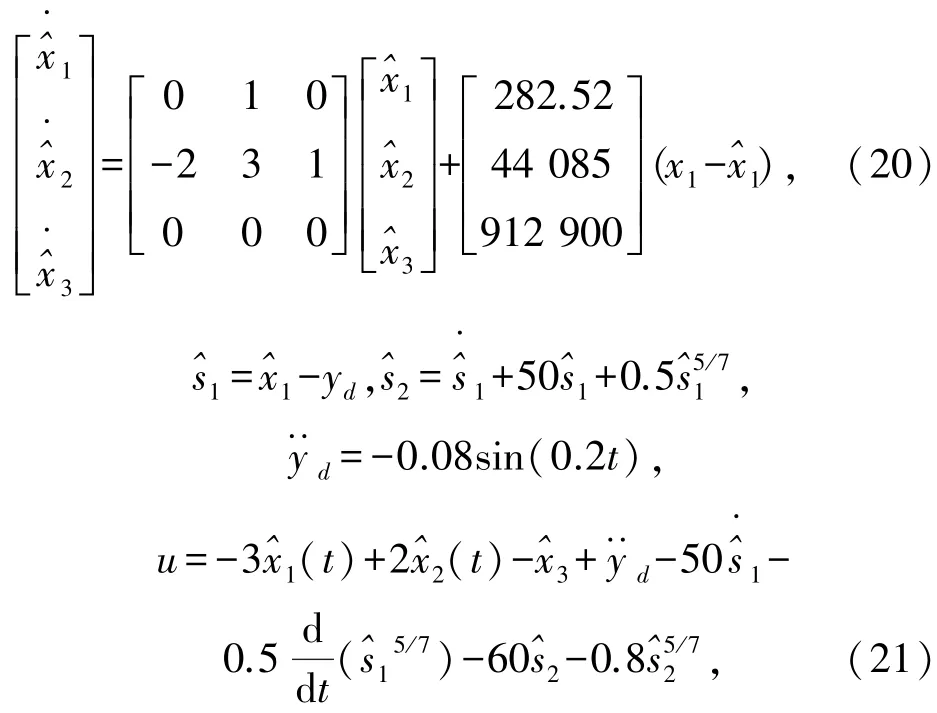
图1～2给出了将控制器（21）应用到系统（19）数值模拟结果。图1（a）说明系统输出曲线、所需信号曲线、跟踪误差曲线，图1（b）分别给出了控制律曲线，由图1（a）可以看到除了某些由LESO的高增益引起的尖点外，跟踪误差非常小，此外，图1中的（b）说明控制量很小。图2表明LESO的跟踪性能，由图2可以看到LESO的输出可以紧密跟踪系统状态及总扰动因素，且误差很小，所以系统状态及总扰动被其估值替代其在系统控制律的设计当中可以被消除。

图1 输出值y，理想信号yd以及控制律u的曲线Fig.1 Trajectories of output y，desired signal ydas well as control law u

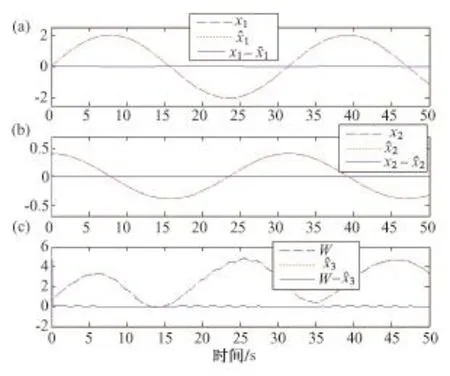
图2 LESO的跟踪性能Fig.2 Tracking performance of LESO

5 结束语

本文对于一类LESO非线性不确定系统提出了基于终端滑模跟踪的LESO算法，这一LESO算法以任意小的误差逼近系统状态以及总扰动参数。该总扰动参数的估计值被用来补偿原系统并进一步实现系统扰动的衰减和消除，本文所提出的终端滑模控制器可以保证系统输出紧密跟踪所需信号，最后数值模拟结果表明所提出的滑模跟踪控制方法是有效的。

［1］Kao Y G，Xie J，Wang C H，et al.A sliding mode approach to H∞non⁃fragile observer⁃based control design for uncertain Markovian neutral⁃type stochastic systems［J］.Automatica，2015，52（1）：218⁃226.

［2］Ma Y C，Zheng Y Q.Projective lag synchronization of Markovian jumping neural networks with mode⁃dependent mixed time⁃delays based on an integral sliding mode controller［J］.Neurocomputing，http：／／dx.doi.org／10.1016／j.neucom.2015.05.062.

［3］Chen B，Niu Y，Zou Y.Adaptive sliding mode control for stochastic Markovian jumping systems with actuator degradation［J］.Automati⁃ca，2013，49（12）：1748⁃1754.

［4］Kao Y，Li W，Wang C.Non⁃fragile observer based H∞sliding mode control for Itstochastic systems with Markovian switching［J］. Robust and Nonlinear Control，2013，24（15）：2035⁃2047.

［5］Khalil H K.Nonlinear Systems［M］.3rd ed.Prentice⁃Hall，Upper Saddle River，NJ，2002.

［6］Hirschorn R M.Generalized sliding⁃mode control for multi⁃input nonlinear systems［J］.IEEE Transactions on Automatic Control，2006，51（9）：1410⁃1422.

［7］Lu X Y，Spurgeon S K.Robust sliding mode control of uncertain nonlinear system［J］.Systems＆ Control Letters，1997，45（2）：75⁃90.

［8］Marquart C A，Zourntos T，Magierowski S，et al.Sliding⁃mode am⁃plitude control techniques for harmonic oscillators［J］.IEEE Trans⁃actions on Circuits and Systems—II Express Briefs，2007，54（11）：1014⁃1028.

［9］Chen C S，Chen W L.Robust adaptive sliding⁃mode control using fuzzy modeling for an inverted⁃pendulum system［J］.IEEE Transac⁃tions on Industrial Electronics，1998，45（2）：297⁃306.

［10］Khan M K，Spurgeon S K.Robust MIMO water level control in in⁃terconnected twin⁃tanks using second order sliding mode control［J］.Control Engineering Practice，2006，14（4）：375⁃386.

［11］Yu X H，Man Z H.Fast terminal sliding⁃mode control design for non⁃linear dynamical systems［J］.IEEE Transactions on Circuits and Systems⁃I Fundamental Theory and Applications，2002，49（2）：261⁃274.

［12］Man Z H，Yu X H.Terminal sliding mode control of MIMO linear systems［J］.IEEE Transactions on Circuits and Systems⁃I，Funda⁃mental Theory and Applications，1997，44（11）：1065⁃1070.

［13］Fridman E.Output regulation of nonlinear systems with delay［J］. Systems＆Control Letters，2003，50（1）：81⁃93.

［14］Yu X H，Man Z H.Multi⁃input uncertain linear systems with termi⁃nal sliding⁃mode control［J］.Automatica，1998，34（3）：389⁃392.

［15］Wei X J，Guo L.Composite disturbance⁃observer⁃based control and terminal sliding mode control for non⁃linear systems with disturb⁃ances［J］.Control，2009，82（6）：1082⁃1098.

［16］Chen M，Chen W H.Sliding mode controller design for a class of uncertain nonlinear system based disturbance observer［J］.Adaptive Control and Signal Processing，2010，24（1）：51⁃64.

［17］Ho H F，Wong Y K，Rad A B.Adaptive fuzzy sliding mode control with chattering elimination fornonlinearSISO systems［J］. Simulation Modeling Practice and Theory，2009，17（8）：1199⁃1210.

［18］韩京清.自抗扰控制器及其应用［J］.控制与决策，1998，13（1）：19⁃23.

［19］Xing Hai⁃Long，Jeon Jin⁃Han，Park K C，et al.Active disturbancerejection control for precise position tracking of ionic polymer⁃metal composite actuators［J］.IEEE ASME Transactions on Mechatronics，2013，18（1）：86⁃95.

［20］Han J Q.From PID to active disturbance rejection control［J］.IEEE Transactions on Industrial Electronics，2009，56（3）：900⁃906.

［21］Gao Z.Scaling and bandwith⁃parameterization based controller tun⁃ing［C］／／Proceedings of the 2003 American Control Conference， Denver，Colorado，USA，2003，4989⁃4996.

［22］韩京清.一类不确定对象的扩张状态观测器［J］.控制与决策，1995，10（1）：85⁃88.

［23］Narendra，K.S.，Balakrishnan，J.A common Lyapunov function for stable LTI systems with commuting A⁃matrice［J］.IEEE Transactions on Automatic Control，1994，39（11）：2469⁃2471.

Composite terminal sliding mode tracking control and extended state observer for SISO nonlinear uncertain systems

ZHONG Xiao⁃zhu1，MA Yue⁃chao2，LIU Jin⁃xian1，XING Hai⁃long3，WANG Zhi⁃li1
（1.Department of Public Courses，Hebei College of Science and Technology，Baoding，Hebei 071000，China；2.College of Science，Yanshan University，Qinhuangdao，Hebei 066004，China；3.Science and Information College，Qingdao Agricultural University，Qingdao，Shangdong 266109，China）

In this paper，the terminal sliding mode tracking control is proposed for the single⁃input and single⁃output systems with known linear dynamics，unknown nonlinear dynamics as well as internal model uncertainties and external disturbance.And the system states are unavailable for measurement.The terms including unknown complicated nonlinear dynamics，internal and external disturbances are defined as total disturbance，and it is considered as an augmented state of model plant.Then this augmented state and the system states can be estimated simultaneously through a linear extended state observer.This method is to design an observer which can guarantee the approximation error to be uniformly ultimately bounded with respect to a ball whose radius is a function of design parameters.So this ball radius can be arbitrarily as small as desired by tuning design parameters.Based on the outputs of the designed linear extended state observer，the terminal sliding mode controller has been proposed，which can guarantee the system out⁃put to closely track the desired signal.Numerical simulation results are given to illustrate the effectiveness of the proposed controller. Key words：sliding mode control；extended state observer；nonlinear system；uniformly ultimately bounded

TP13

A

10．3969／j．issn．1007⁃791X．2015．05．008

1007⁃791X（2015）05⁃0431⁃07

2015⁃02⁃20 基金项目：国家自然科学基金资助项目（61273004）；河北省自然科学基金资助项目（F2014203085）

钟晓珠（1948⁃），男，河北乐亭人，教授，主要研究方向为差分方程理论、控制理论；∗通信作者：马跃超（1963⁃），男，辽宁凤城人，教授，博士生导师，主要研究方向为控制理论，Email：myc6363＠126.com。