强化数据分析 培养主体意识

陈士才

所谓数据分析，就是学生在教师的指导下，产生采集数据的意识，选择合适的分析方法，自主运用数据进行分析，体验数据分析后的乐趣，运用数据解决实际问题，从小养成用数据分析问题、用数据说话的习惯。

一、由因索果：经历数据采集的过程

要会正确地进行数据分析，首先要使学生养成采集数据的习惯，亲身经历数据分析的过程，并对采集的数据进行比较、分析，发现规律性的东西。在进行数据分析的时候，是由因索果，而不是先入为主、由果索因，否则就失去了数据分析的本来意义。

在教学五年级下册《圆的周长》计算圆周率π的值时，教师可指导学生分组操作测量圆的周长和直径，有的学生用线绕圆片一周，有的把圆片放在直尺上滚动一周，用各种方法测量圆周的周长，再与直径进行比较，求比值后填入表格。

周长和直径的数据都是学生测量出来的，因此，有大有小，各不相同。在填写“周长除以直径的商”这一栏时，有的学生用笔进行计算，有的学生用计算器计算。最后观察这些数据，都在3左右。但是也有少量学生已经看了书上的答案，不愿意进行繁难的计算，直接就在这一栏目填写3或者3.14，这样直接写出的结果，对于数据分析就毫无意义了。

实际上，由于学生测量周长与直径的准确度各不相同，有一定的误差，计算出π的值也有差距，但我们在课堂上，用十分有限的时间计算出圆周率在3左右，已经很不错了，如果我们连这点计算都怕麻烦，不像古人计算圆周率那样孜孜以求，今后怎么能够有所成就呢？所以对数据的采集，一定要实事求是，采取科学、勤奋的态度。

二、殊途同归：拓展数据转化的路径

小数、分数、百分数，有时就可以用线段或者图形来表示，这样可以更加直观简单地把握数据的特征，探求解题的思路，快速准确地求出答案。

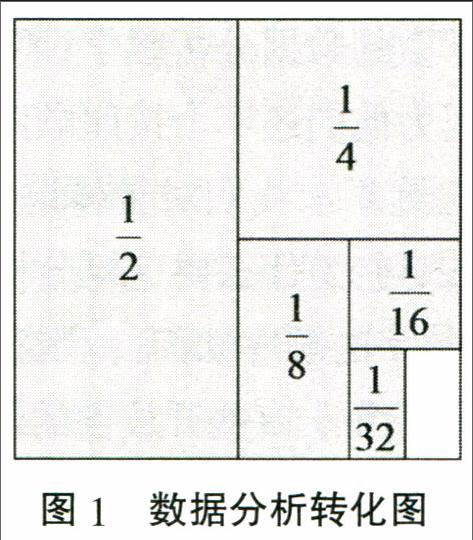
在学习完六年级下册《解决问题的策略——转化》之后，有这样一道尝试题：计算1/2+1/4+1/8+1/16+1/32。一般学生用通分的方法：16+8+4+2+1/32=31/32，也有的学生将前面2个数相加，用加的和与后一个数相加，一直到最后。

学习过转化的知识之后，教师要引导学生分析这些数据。当然，还有的学生对数据进行分析，发现这道算式还可以转化为图形来表示：

求1/2+1/4+1/8+1/16+1/31的和，实际上是求图中阴影部分的面积，整个正方形用1表示，阴影部分的面积就等于1减去空白部分的面积，也就是1-1/32=31/32。这样，让学生明白，具有一定规律的算式，可以转化为图形来计算。

三、举一反三：寻找数据之间的规律

许多数据，如果我们单一地看，似乎没有什么联系，但当我们把这些数据放到一起进行比较时，就很容易发现它们之间有某种内在的联系。教学时，我们要善于引导学生将数据前后进行比较，上下关联，找出规律，再利用规律来解决问题。

例如，在学习完六年级“解决问题的策略——转化”之后，教师可设计一道练习题：一个三角形的内角和是180度，那么，一个20边形的内角和是多少度？

这些图形的边数与它的内角和之间有什么关系呢？我们来观察这些数据：一个三角形时，有3条边，1个三角形的内角和就是180°；一个四边形时，有4条边，相当于2个三角形的内角和就是360°……

可见，图形的边数总是比三角形的个数多2，反过来，边数减去2就是三角形的个数，故内角和=180×（边数-2），这样得出规律，那么20边形的内角和度数就是180×（20-2）。

四、一一列举：掌握数据变化的顺序

对低年级学生的数据分析教学，要考虑到学生的年龄实际。因为他们还不会按照顺序来观察，不会抽象概括。这就要求我们对具体题目要具体分析，让其慢慢意识到：为什么要这样分析数据，分析的依据是什么，数字的顺序如何，范围怎么样，这样做对吗，怎么进行验证。有些开放性的题目，答案不是唯一的，在指导解题时，我们还要逐一尝试，一一列举。

在学习完一年级下册进位加法之后，教师可以设计这样一道题目：25+□=2□；25+□=3□。

这是一道开放题，目的在于让学生思考什么情况下进位，什么情况下不进位。到底口里填写什么数？这就要进行数据分析。因为是两个未知数要填，故它是一个动态的过程，和的条件决定了前面一个加数的范围，而一旦前一个加数被确定下来，最后的和的计算结果也就出来了，这个结果还可以验证其和是否满足条件。这对一年级小学生来说，有一定难度。

我们可这样引导学生分析，第一题，一个加数是25，和是2□，也就是第一个加数个位上的5与第二个加数□加起来应该小于或等于9，而超过一个数就是10，最后的结果是和便要超过2□，不符合条件。那么，5加什么数小于或等于9？让学生一一列举出来，按照顺序分别是0、1、2、3、4，学生一一相加，后面的和随着前面加数的变化而变化，相加的结果分别是25、26，27、28、29。同样，第二小题的数据分析，也是让学生进行数据分析……相加的结果分别是30、31、32、33、34。

五、观察图表：发现数据背后的信息

小学阶段的教材中出现了很多图表，有的是统计图表，也有的是几何类的、算式类的图表，这些图表在教学时都有一个重要的目标，就是鼓励学生能够从统计图表中主动发现、获取尽可能多的有用数据。

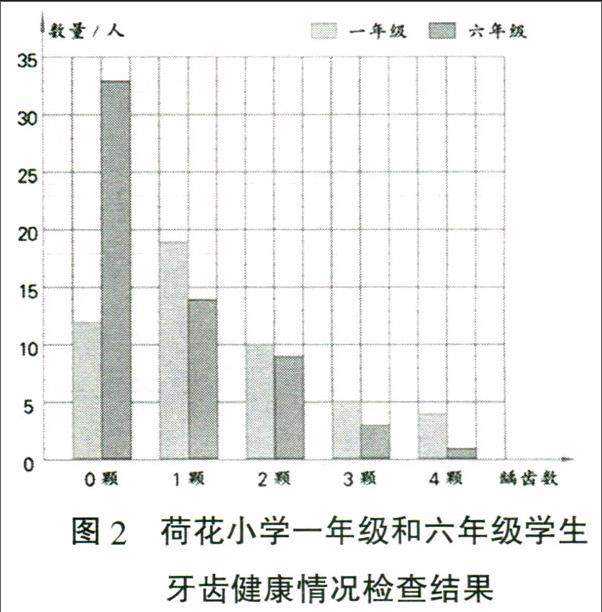
下图是六年级下册总复习中的一个统计图，这幅图中蕴含着丰富的信息，教学时可以着重从以下几个方面引导学生发现信息。

第一，读从统计图中能直接看到的信息，比如单个数据的多少，统计图的名称和图标。引导学生分析：这是个什么统计图？图中两种不同颜色的条形分别表示什么？把数据在条形上面标出来，说说这两个年级学生牙齿的健康情况。

第二，读经过简单推理能得到的信息，包括数据的比较（多少、倍数、百分比等）和数据的整体变化（最大、最小、平均情况、变化情况、偏差、极端数据等）。引导学生分析：两个年级学生龋齿颗数的人数分别是多少？一年级学生一共有多少颗龋齿？六年级呢？两个年级平均每人各有多少颗龋齿？哪个年级学生的牙齿健康状况好一些？

第三，对数据的解释和预测，数据是蕴含着信息的，光看见了数字还不够，还要去思考、去解释、去判断、去预测，包括统计数据能否帮助我们解决其他问题、能否进行预测，为什么数据会呈现这种情况等。在这个统计图中，在对前面的一些数据进行了解、计算、推理后，可以让学生试着思考数据后面隐藏的信息：为什么六年级学生的牙齿健康状况会好于一年级，一年级学生可能是什么原因导致牙齿健康状况不好，你对一年级学生有什么建议？

六、纵横对比：内化数据运算的法则

小学阶段，计算教学是重要的教学内容，在进行计算教学时，自然离不开对数据的观察与分析。教师要善于引导学生捕捉数据以及由数据组成的算式之间的联系，对不同形式的算式进行对比，可从中发现共同之处，找到计算的规律，归纳出计算的法则，深化对计算法则的认同与理解。

如三年级下册“两位数乘两位数的笔算”的教学，学生有了预习的基础后，可通过以下教学步骤达到对计算法则的深刻理解。

①在对旧知识复习回忆的基础上，出示情境图（略）：每张学生票要62元，35位学生一共要多少元？

设问：怎么列式？（板书：62×35）交流：你能用什么方法算出得数呢？教师板书……看来这一种分步算的方法真不错，两位数乘两位数都可以用这样的方法。但这方法就是写的时候太麻烦，怎么办呢？对，列竖式，可以把这个计算过程简化成竖式。

学生提出的结合具体情境进行分步计算的方法，正是竖式计算的算理，当学生得出这种两位数乘两位数的通用算法后，教师引导学生感受横式分步计算方法的繁琐，然后产生简化为竖式计算的需要，便感受到用竖式计算的价值。

②以学生交流预习时的竖式计算过程，引导学生思考：竖式计算的这三步实际上是刚才横式算法中的哪一步？教师将横式与竖式的每一步用箭头对应起来。

学生通过预习，知道了竖式计算的形式，更要理解形式后面的道理，所以，此环节要在教师的引导下，生生互动、师生互动，重点交流讨论部分积的书写位置以及为什么这样写，更与前面讨论的横式算法相联系，用算理指导算法，用算法验证算理，深刻理解计算法则。

③谈话：两位数乘两位数，用竖式计算非常简洁，那么，古代人们是怎么计算两位数乘两位数的呢？请同学们看一段介绍（课件介绍“铺地锦”的计算方法）。这种铺地锦的计算方法看起来好像挺复杂，其实它和我们今天学的竖式计算在道理上是相通的（课件展示：把竖式计算的两个部分积分解为四个部分，并用不同色条标出三种算法的联系之处，图略）。

“铺地锦”是教材后面“你知道吗？”栏目的内容，这种方法与竖式方法及横式分步计算的方法在算理上是一致的，通过这样三种计算方法的沟通与对比，学生将会更加深刻地理解算理，感受竖式算法的简洁性。

小学数学教学就是要使学生产生对数据的亲切感，遇到实际问题时愿意去收集数据，并经历处理数据、利用数据分析问题、获取信息的过程，从而达到帮助解决问题的目的。只有这样，才能真正地培养学生的“数据分析观念”，培养学生的主体性，使学生的数学思想得到更全面的发展。

（编辑 刘泽刚）