基于SPSS的高层建筑物沉降预计模型研究
2015-12-11朱庆伟杨传福
朱庆伟,杨传福
(西安科技大学测绘科学与技术学院,陕西西安710054)
一、引 言
随着高层建筑数量越来越多,施工过程中发生重大事故或竣工完成后楼房倒塌的事件屡见不鲜。《高层建筑混凝土结构技术规程》(JGJ 3—2010)中规定:10层及10层以上或高度超过28 m的钢筋混凝土结构称为高层建筑结构[1]。当建筑高度超过100 m时,称为超高层建筑。由于高层建筑大多结构复杂,荷载大,或是由于地基土层较软,受力不平衡等原因,势必导致基础发生较大的沉降或不均匀沉降[2]。建筑物的沉降会影响正常施工和施工方案的调整。在施工期间和竣工后的使用期间都有必要对建筑定期进行有计划的沉降观测,获取大量观测数据[3-4]。在此基础上,对观测数据进行整理,试图找出沉降规律,进而为后续施工提供有价值的参考和指导。
本文主要利用了SPSS软件进行曲线拟合,模拟出沉降预计表达式,并结合实例进行分析,证明了这种模型具有较高的可靠度与可行性。
二、回归原理
不管是线性回归、曲线回归,还是非线性回归,都是建立在大量数据和统计资料的基础上进行的因变量与自变量之间的拟合关系[5]。一般来说,若两个变量之间呈线性关系比较容易拟合;若变量之间呈非线性关系,应根据变量之间的散点图选取较为合适的模型进行拟合。
1.线性回归
线性回归方程一般设为

为了保证各散点(实测点)与回归直线间的距离平方和最小,可采用最小二乘法推导出a、b值[6]。公式如下
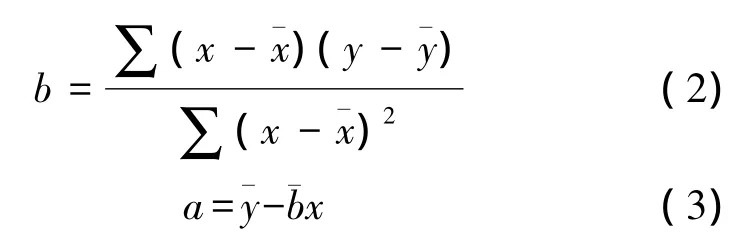
2.曲线回归
当两个变量间的关系呈非线性关系时,应考虑进行曲线拟合。曲线拟合就是近似反映变量之间曲线关系的过程。常用的曲线拟合模型有二次方程(Quadratic)模型、复合曲线(Compound)模型、对数方程(Logarithmic)模型、S型曲线(S)模型、三次方程(Cubic)模型等[5]。
在进行曲线拟合时,需要指出的是:如果x的某种变换z与y呈线性关系,则可采用“曲线直线化”的方法对z与 y进行线性拟合[5]。如,^y=a+bln x,令z=ln x,进而对z和y做最小二乘拟合。同样,也可对y进行适当变换,以便进行最小二乘拟合。
三、检验方法
在一般线性回归中,反映两个变量之间的关系密切程度或数量上的影响大小是比较回归系数或相关系数的绝对值,并不是用概率值P来判断。
P值越小只能说明变量间的关系存在的理由越充分,并不能说明两者之间的关系密切程度。
线性相关系数又称Pearson积差相关系数,常用 R 表示[5-6]
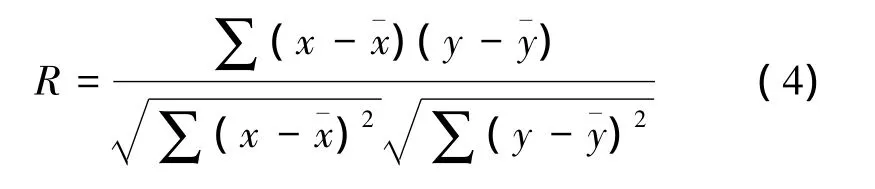
式中,|R|≤1。R<0,表示负相关;R>0,表示正相关;R=0,表示零相关;|R|=1,表示完全相关。
在曲线拟合和非线性拟合的结果检验中常用决定系数R2衡量。
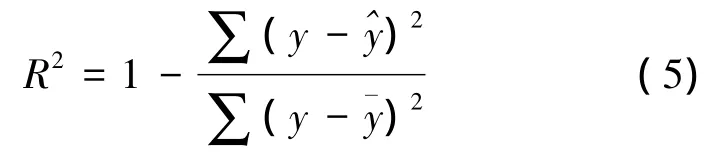
一般来说,R2越大拟合度越高,拟合效果越好。
四、SPSS软件在实例中的应用
1.SPSS软件
SPSS(statistical package for the social science)是由SPSS公司出品的大型通用专业统计分析软件。该软件能够通过利用多种类型的数据文件及数据源,生成统计报表、统计图形,进行简单和复杂的统计分析[5]。
2.实例分析
2013年8月至2013年12月对西安市某高层定期进行了15次沉降观测,每次观测结果均满足国家二等水准测量精度要求,具有研究价值。操作流程如图1所示。
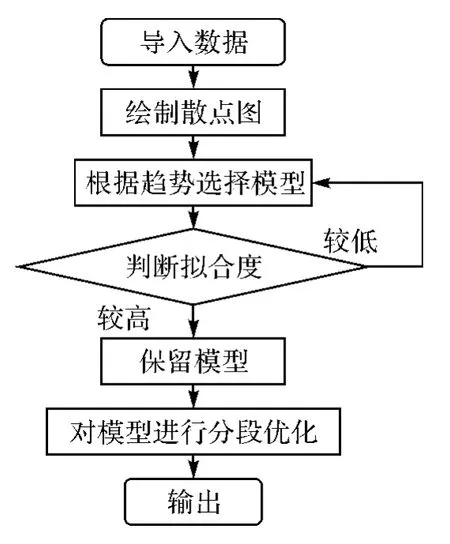
图1 操作流程
由图2散点图知,观测值随时间递增,且大致呈曲线分布,故选择 Linear、Cubic、Quadratic、Compound 4种模型进行拟合。由图3可知,Linear、Cubic、Quadratic模型较为符合真实值变化趋势,进而对这3种模型的结果进行分析比较(见表1),选出更为合适的模型进行沉降预计。
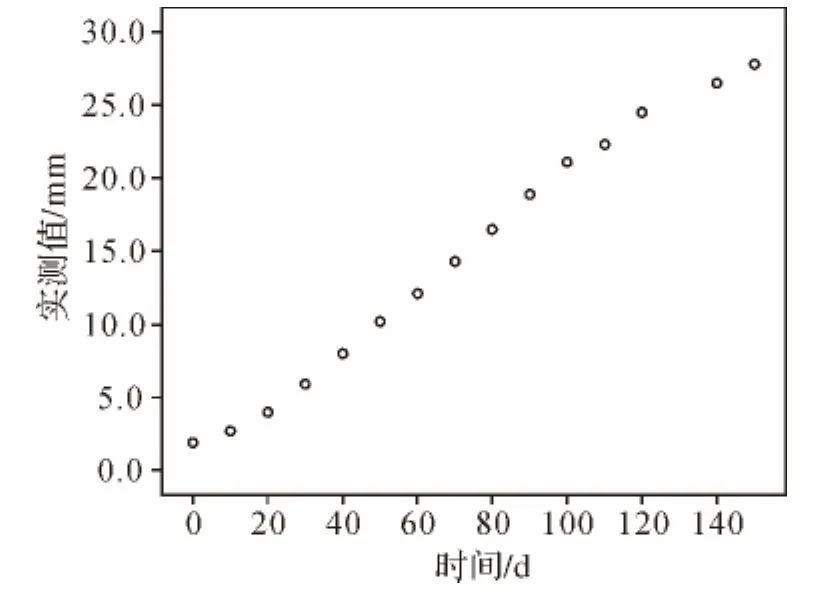
图2 散点图
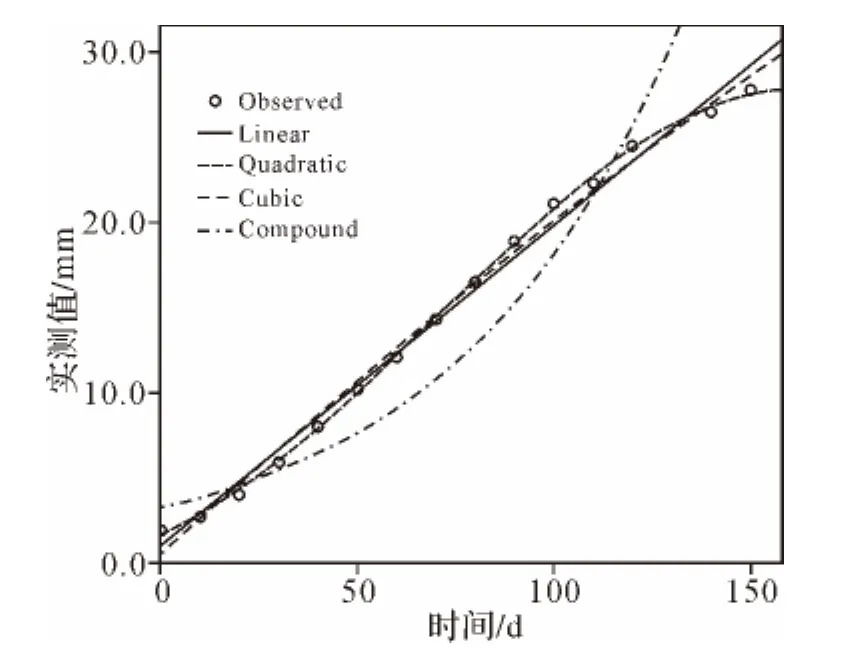
图3 多种模型拟合曲线
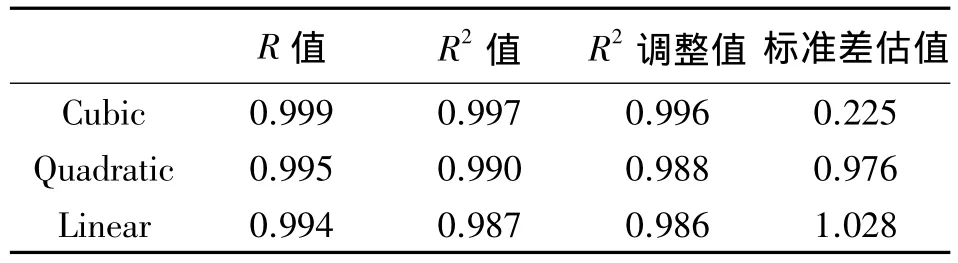
表1 不同模型比较
根据3种模型的比较结果,Cubic模型最为符合真实值情况(R=0.999,R2=0.997),根据表 2 拟合式系数可直接得出回归方程为
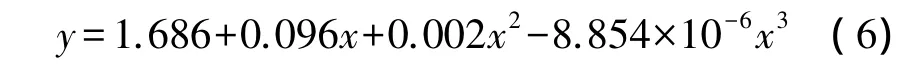
再通过式(6)可得到任意监测点(以C3点为例)的拟合值,结果见表3。
根据统计学原理知,所得拟合值有很高的可信度,且该模型能够很好地反映实际情况。
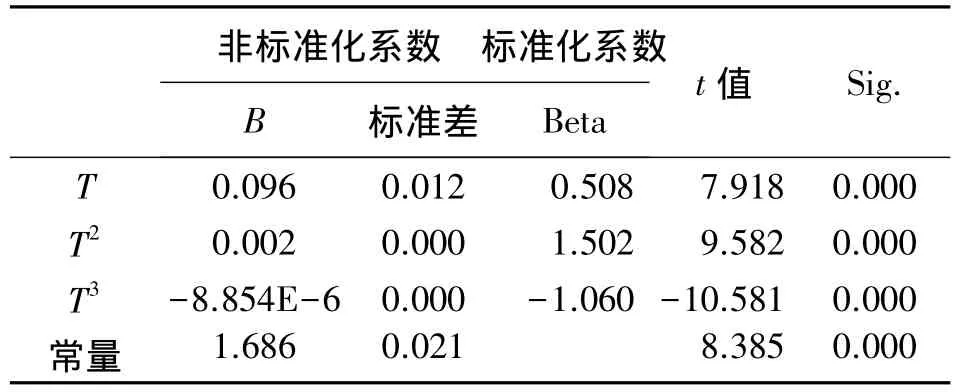
表2 拟合式系数
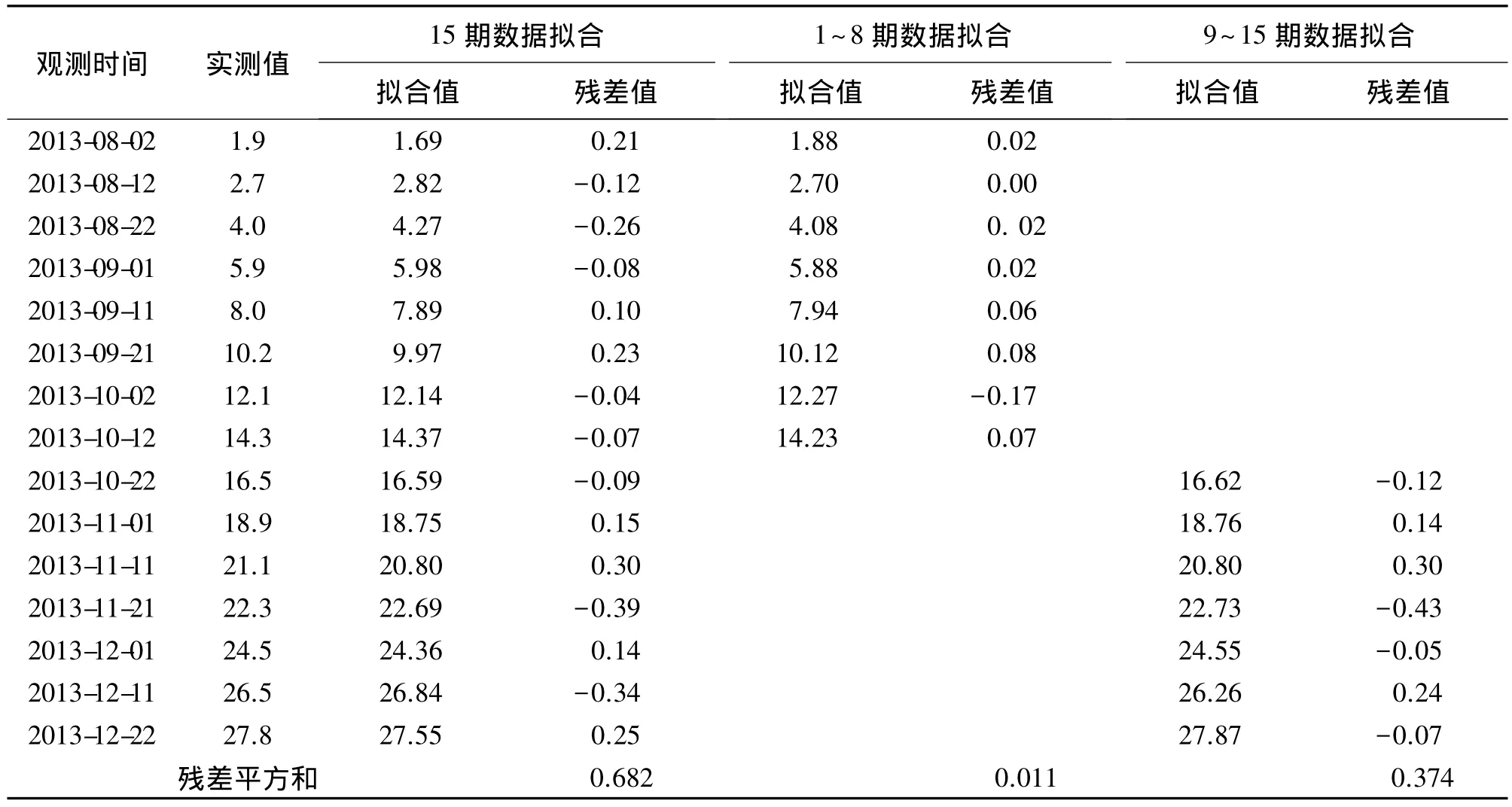
表3 拟合值与实测值的对比 mm
3.拟合优化
为了进一步优化模型,提高拟合效果,在Cubic模型的基础上进行分段拟合。首先,由图2可知,1~8期数据为非线性关系,9~15期的数据更接近于线性关系,分别对1~8期数据(如图4所示)和9~15期数据进行拟合[7-10](如图5所示),得到回归方程为
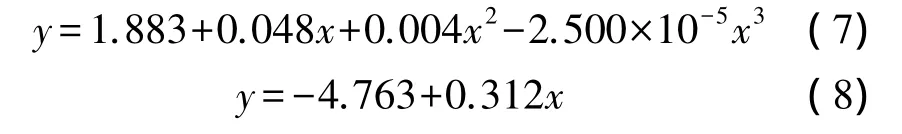
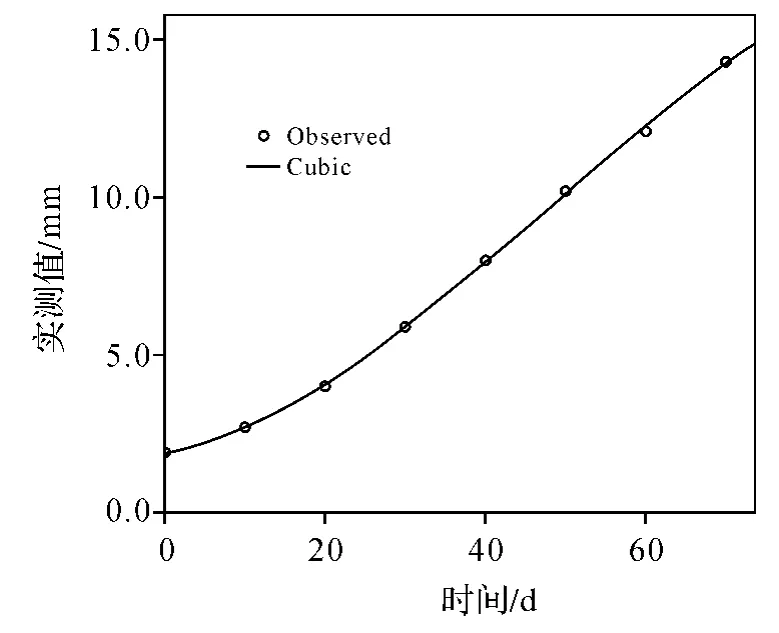
图4 1~8期数据拟合效果
然后,分析拟合结果并与整体拟合结果作比较。两次拟合结果的决定系数R2均为0.999,可认为拟合效果都有很高的可靠性和可信度。
两次拟合的残差平方和为0.385 mm2,小于整体拟合的残差值平方和0.628 mm2,可以认为模型拟合效果得到了提高。
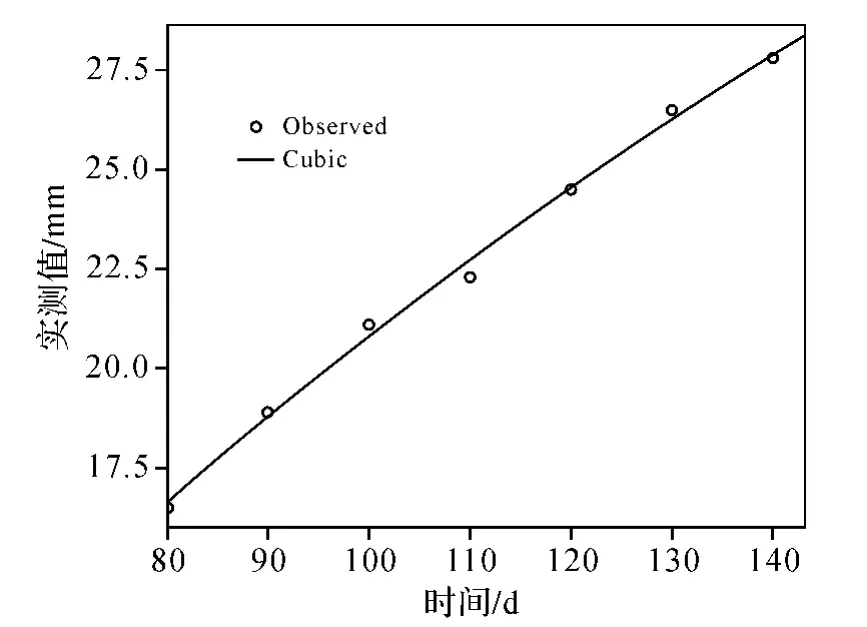
图5 9~15期数据拟合效果
不同回归方程的拟合值见表3,可用式(8)对后期数据进行预计,同时可用式(7)对前期数据进行缺失弥补。
4.实例验证
为了验证此方法的可行性,取同期观测的C5点的实测数据(见表4)进行验证。处理流程同上,对该点沉降数据分别进行整体曲线拟合和分段拟合,并比较其精度。由于两种拟合结果与实测值的差值很小,为了更直观地比较其精度与拟合效果,用Excel绘制出它们的残差图[11],如图6所示。
尽管第11期和第12期数据的残差值相对较大,且第12期数据分段拟合的残差值大于第11期数据,但从整体来看,分段拟合效果更佳(见表5)。

表5 整体拟合与分段拟合比较
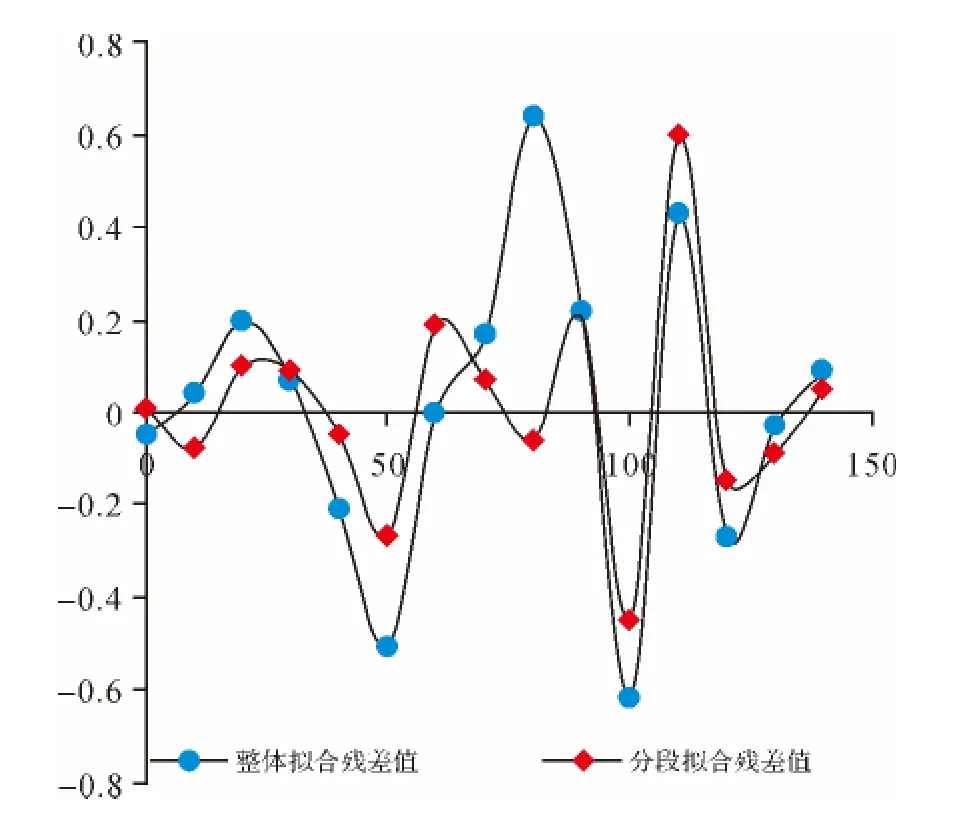
图6 残差值比较
五、结 论
1)在回归分析中,SPSS软件能够通过简单的操作拟合出不同曲线,且能够通过拟合过程的分析结果直接写出函数表达式。
2)通过本文试验可知,基于SPSS的曲线拟合有一定的可靠性。经实例验证,分段拟合效果优于整体拟合效果,可利用此方法对各观测点进行沉降预计,以保证施工安全与建筑物质量。
3)如结合实地物理模型,工程结构并进行力学分析等,则拟合效果会更好。
[1]JGJ 3—2010高层建筑混凝土结构技术规程[S].北京:中国建筑工业出版社,2001.
[2]陈伟清.建筑物沉降变形分析与预测技术应用[J].勘察科学技术,2007(3):53-55.
[3]温宇斌.建筑物沉降观测的实践及探讨[J].测绘通报,2002(11):37-39.
[4]崔国宏,徐礼华.土木工程建筑物变形分析与预报技术研究[J].地理空间信息,2004(3):10-12.
[5]宇传华.SPSS与统计分析[M].北京:电子工业出版社,2007.
[6]黄声享,尹晖,蒋征.变形监测数据处理[M].武汉:武汉大学出版社,2010.
[7]刘玉成,王坤,范育青.沉陷盆地倾向主断面下沉曲线拟合研究[J].中国矿业,2011,20(4):71-73.
[8]曹慧.统计学:基于SPSS的应用[M].北京:北京大学出版社,2013.
[9]邹述超,何腊梅,徐友才.概率论与数理统计[M].北京:高等教育出版社,2014.
[10]曹树刚,刘玉成,刘延保,等.基于观测资料的沉陷盆地主断面曲线拟合[J].重庆大学学报,2009,32(7):804-808.
[11]王鹏,孟灵飞,李蓬,等.回归分析在建筑物变形监测中的应用[J].测绘科学,2013,38(2):187-188.
