GPS单频实时动态定位研究与实现

周 鹏，刘 晖，2，钱 闯

(1.武汉大学卫星导航定位技术研究中心，湖北武汉430079;2.武汉导航与位置服务工业技术研究院，湖北武汉430075)

一、引 言

通过时间更新过程和量测更新过程，卡尔曼滤波对待估参数进行预测与修正，由于卡尔曼滤波的整个更新过程是循环递推的，因此滤波器无须存储太多的历史数据，使用当前观测数据即可实时获得被估计参数的最优估计值。由于这个特点，卡尔曼滤波从一提出就受到各工程应用领域的青睐，尤其是实时动态数据处理领域，如高精度组合导航［1］与GPS动态定位。

在城市峡谷等复杂观测环境下，由于卫星信号遮挡严重，可见卫星数量不多且卫星可视情况并不连续，加上复杂环境下多路径效应等外部干扰因素的影响，不易确定观测序列噪声特性，这对滤波器的稳定性和模型精度有了更高的要求。针对这个缺陷，本文提出了观测序列噪声方差-协方差阵的自适应确定方法，对动态卡尔曼滤波算法进行了优化，加上原始观测量的粗差探测。多次路测试验表明，该算法稳定可靠，在普通的城市道路上，优化算法能显著提高GPS动态定位的效果，得到较为理想的定位结果。

二、GPS动态卡尔曼滤波模型

1.卡尔曼滤波参数估计原理

利用卡尔曼滤波进行动态系统参数估计首先需要确定系统的状态方程和观测方程，对于离散线性系统，通用的卡尔曼滤波状态方程和观测方程为［2-3］

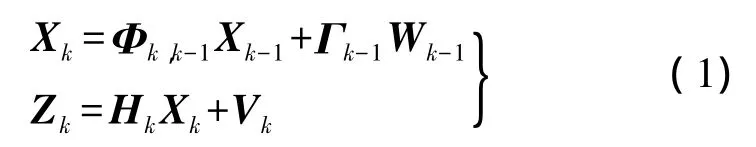
式中，Xk为 tk时刻的系统状态向量;Φk，k－1为 tk－1至tk时刻的系统状态转移矩阵;Γk－1为系统噪声驱动矩阵;Wk－1是动态噪声序列;Zk为tk时刻的观测向量;Hk为观测方程系数阵;Vk为观测噪声序列。

系统随机模型满足以下要求

式中，Qk为动态噪声序列Wk－1的方差-协方差阵;Rk为观测噪声序列 Vk的方差-协方差阵;δkj为 Dirac 函数［2］。

若状态向量Xk与观测向量Zk满足式(1)，动态噪声序列Wk－1与观测噪声序列Vk满足式(2)，且动态噪声方差-协方差阵非负定，观测噪声方差-协方差阵正定，则tk时刻状态向量Xk的估计值

估计均方误差为

2.动力学模型的构建

对于GPS动态定位，由于信息的缺失，难以构建精确的动态定位模型来描述载体的运动，在损失一定精度的条件下，可对载体运动模型进行简化，本文采用应用较多的常速模型(CV模型)［4］。

CV模型中选定状态向量为

式中，(xk，yk，zk)为接收机的WGS-84地心坐标分别为接收机3个方向上的速度;dtk、d˙tk分别为接收机钟差与钟差变化率。

根据式(1)，可知状态转移矩阵 Φk，k－1为

据文献［5］可知，动态噪声序列 Wk－1的方差-协方差阵Qk为

式中，Sp、Sf、Sg分别为接收机状态、钟差、钟差变化率的谱密度，分别取值 1.0、0.4×10－18、1.58×10－18［5］。

滤波过程中，使用伪距单点定位结果作为滤波初始值。另外，当较长时间无法定位(卫星数不足)时需重新初始化。

3.观测模型的构建

关于GPS观测方程，给出其定义如下［6］

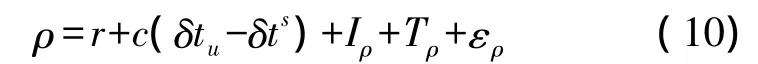
式中，ρ为伪距观测值;r、c分别为卫星与接收机间的几何距离和光速;δtu、δts分别为接收机钟差与卫星钟差;Iρ、Tρ分别为电离层延迟与对流层延迟，单位为m;ερ为其他误差的综合项，单位为m。

进行PVT(position velocity and time)解算时，需采用卫星信噪比cn0确定观测噪声序列的方差-协方差阵Rk，具体为

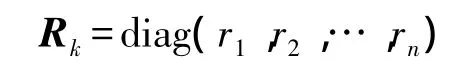
式中，ri取值为

上式中相关参数为经验参数，与模块相关。

三、测试与分析

1.测 试

为测试算法的正确性，对PVT定位程序进行了路测，部分测试环境如图1所示。

图1 测试环境

测试天线使用普通的导航天线，模块为u-blox LEA-6T模块(设置测试采样率为1 s，实际测试过程中也使用了其他模块，效果一样)，测试方法如下:

1)设备安置。将导航天线固定于测试车车顶并连接至模块的天线输入端，同时使用数据线连接模块和计算机，使得模块的实时观测数据可以流入计算机并交给PVT程序。

2)模块设置。为模块通电，通过模块的控制软件U-Center对模块的工作方式、数据输出等进行设置，并保存。

3)开始测试。启动PVT程序，进行实时PVT解算。

为形成参照，分析PVT定位程序的解算精度，在测试车车顶的导航天线旁边安置Trimble R10便携接收机，该接收机连接湖北省连续运行参考站系统(HBCORS)，工作模式为RTK。

2.对比分析

为说明本算法相比伪距单点定位精度有很大改善，在事后进行了伪距单点定位解算，这样加上实时解算的结果，就获得了3组数据:

1)PVT定位程序实时解算结果。

2)Trimble R10的实时RTK解算结果。

3)事后伪距单点定位解算结果。

众所周知，RTK固定解精度很高，因此在进行伪距PVT解算精度分析过程中，以同步的RTK固定解为参考值，比较PVT定位程序实时解算结果与事后伪距单点定位解算结果相对同步RTK固定解在水平、竖直方向的偏差(如图2、图3所示)。

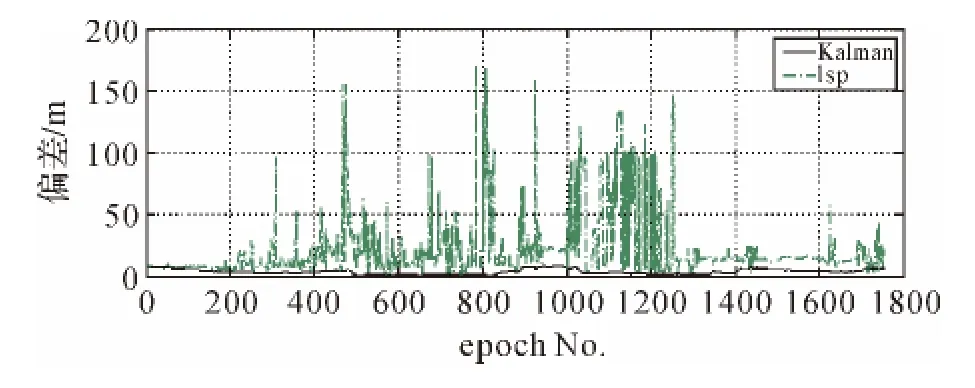
图2 最小二乘与卡尔曼滤波对比(水平方向)

图3 最小二乘与卡尔曼滤波对比(竖直方向)

比较图2与图3可见，改进的动态卡尔曼滤波算法相比最小二乘算法，不论是水平方向还是竖直方向，定位效果都提高很多。

为便于定量分析，给出实时解算结果与事后最小二乘解算结果在各个误差段的统计信息，由于关注的是平面位置，下面仅给出水平方向上的误差统计(见表1)。

表1 最小二乘与卡尔曼滤波解算结果误差统计(%)

从表1可见，优化的实时卡尔曼滤波算法超过70%历元水平精度优于5 m，所有定位结果水平精度均优于10 m;而最小二乘算法中，水平精度优于5 m的历元不到10%，多数历元水平精度介于7～30 m(70%)。相比最小二乘算法，优化的实时卡尔曼滤波算法解算精度提高很多。

四、结束语

本文研究了在城市道路下使用低成本导航天线与电子消费类GPS模块进行实时动态定位的方法，算法中仅使用单频伪距和多普勒观测值，对系统成本要求不高。算法以动态卡尔曼滤波为基础，加上基于卫星信噪比的观测序列噪声方差-协方差阵自适应确定方法，克服了复杂环境下GPS定位效果差的缺点。相比最小二乘算法，本算法定位效果有很大提高，通过实时解算测试说明，在城市街区，超过70%历元水平精度优于5 m，所有历元水平精度优于10 m。

［1］秦永元.卡尔曼滤波与组合导航原理［M］.西安:西北工业大学出版社，1999:2-3.

［2］GELB A.Applied Optimal Estimation［M］.Cambridge:MIT Press，2001:72-74.

［3］蔡艳辉，程鹏飞，李夕银.用卡尔曼滤波进行GPS动态定位［J］.测绘通报，2006(7):6-8.

［4］董绪荣，陶大欣.一个快速Kalman滤波方法及其在GPS动态数据处理中的应用［J］.测绘学报，1997，26(3):221-227.

［5］JWO D J，WANG S H.Adaptive Fuzzy Strong Tracking Extended Kalman Filtering for GPS Navigation［J］.IEEE Sensors Journal，2007，7(5):778-789.

［6］MISRA P，ENGE P.Global Positioning System:Signals，Measurements，and Performance［M］.2nd ed.Massachusetts:Ganga-Jamuna Press，2006:200.

［7］宋迎春，朱建军，陈正阳.动态定位中测量噪声时间相关的 Kalman滤波［J］.测绘学报，2006，35(4):328-332.

［8］龚真春，陈安宁，李平，等.GPS动态定位中自适应卡尔曼滤波方法的应用研究［J］.测绘通报，2006(7):9-12.

［9］单瑞，赵铁虎，于得水，等.单点GPS多普勒测速模型比较与精度分析［J］.测绘通报，2013(3):7-10.

［10］赵玉凤，徐建华，何文涛，等.一种利用多普勒频移平滑伪距的方法:中国，101865992A［P］.2010-10-20.