基于各向异性的自适应拟合推估及其在缺失数据拟合中的应用

郝 蓉，张菊清

(长安大学地质工程与测绘学院，陕西西安710054)

一、引 言

InSAR由于具有高精度、高分辨率等特点，是目前地表变化监测的一种重要手段。然而，由于受时间、空间去相干等因素的影响，提取的形变信息中经常存有缺失现象，需要后期对其进行填补处理。对于缺失数据的拟合，常采用空间数据插值方法进行拟合填补。根据模型不同，空间数据插值法可分为函数模型法和随机模型法两种［1］。常用的函数模型法有曲线内插法、曲面内插法、多面函数内插法、多项式内插法及移动曲面拟合法等，随机模型法主要有反距离加权法、Kriging插值法和拟合推估法等。

在众多的插值和拟合方法中，拟合推估由于其既能较好地反映趋势性变化成分，又能很好地刻画带有局部相关性的随机特征，已广泛应用于重力场推估［2-4］、高程转换［5-7］、地壳形变分析［8-10］、地图数字化纠正及坐标变换［11-14］之中。然而在拟合推估求解过程中，随机信号协方差函数的确定是难点和关键，已引起众多学者的关注。刘念等针对异常误差对观测值的影响提出了协方差函数的抗差拟合方法［15-16］;刘汉江等结合拟合推估实际应用，进行了局部协方差函数的拟合研究［17-18］;金保平等则利用遗传规划理论研究了协方差函数的确定问题［19］。考虑到经拟合得到的信号向量协方差与观测向量的先验协方差很难一致，进而影响推估精度的问题，杨元喜等提出了应用方差分量估计方法来重新调整信号向量与观测向量的先验权比［20-21］，并在此基础上进一步提出了自适应拟合推估方法，即利用方差分量估计构建观测误差与随机信号之间的自适应因子，以此来调整观测向量与信号向量对模型参数估计的贡献［22-23］，并在高程转换、地壳形变分析等领域得到了很好的应用。

然而，现有的协方差函数大都是基于随机信号具有各向同性的二阶宽平稳随机过程的假设条件完成的，而实际上各向异性现象更加普遍。Steffen H G针对大气噪声的各向异性进行了协方差函数的拟合研究，并有效地改善了形变监测精度［24］。考虑到变异函数具有刻画区域化变量的结构性和随机性的能力，它通过本身的结构及各项参数可以从不同角度反映空间的变异特性［25］，进而能更好地展现空间变量的异常特征，突出异常的局部变化性和空间结构信息。基于此，本文提出利用几何各向异性的特性，借助变异函数并通过线性变换将随机信号由各向异性转换为各向同性，在此基础上拟合协方差函数，并通过方差分量估计构建自适应因子，以此调节观测噪声与随机信号对拟合推估解的影响，最后将其应用于InSAR缺失数据的拟合后处理中。

二、变异函数与协方差函数

变异函数是地统计学特有的基本工具，它既可以描述区域化变量的空间结构性，又可以解释其随机性。变异函数可表示为

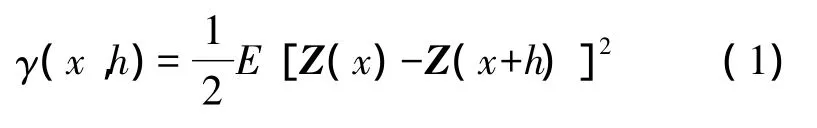
式中，γ为变异函数;Z为区域化变量;E()表示数学期望。若随机变量Z具有二阶宽平稳随机特性，则其变异函数γ仅与距离h有关，与位置x无关。于是式(1)可简写为

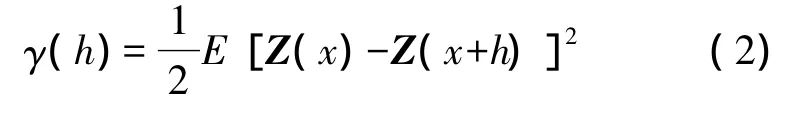
显然，变异函数反映的是数据空间不相关程度与其距离的关系。从式(2)可以看出，空间不相关程度随距离的增大而增大。

协方差函数是另一种表达空间相关性的量，可定义为:随机场Z(x)在空间点x与x+h处的两个随机变量Z(x)与Z(x+h)的二阶混合中心距，即

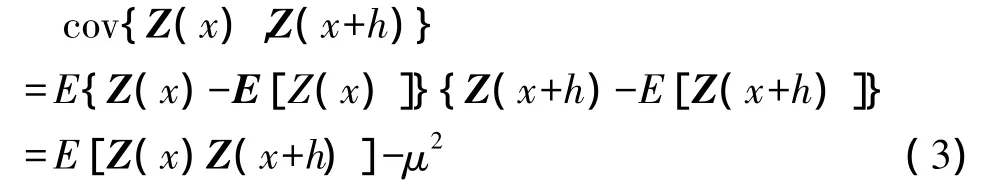
式中，μ为随机向量的期望值。

可以证明，在二阶宽平稳假设条件下，随机向量Z(x)的协方差函数C(h)和变异函数γ(h)之间具有如下的函数关系

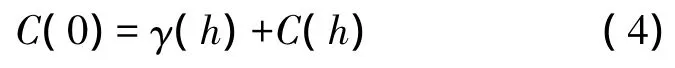
式(4)可理解为先验方差C(0)等于协方差与变异函数之和。其关系曲线如图1所示。

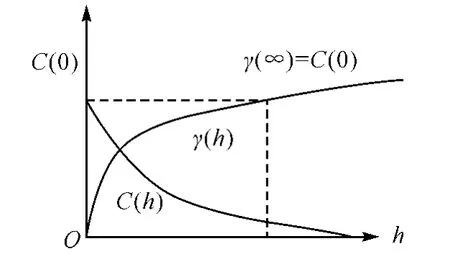
图1 协方差函数和变异函数关系

显然，协方差函数反映的是区域化变量的相关程度，而变异函数反映的则是区域化变量的变异程度，它们从两个不同侧面反映了区域化变量间的关系。

三、基于各向异性协方差函数的拟合

1.各向同性协方差函数的拟合

随机信号协方差函数的确定是拟合推估求解的关键。由于协方差函数的严密表达式往往很难获得，通常利用观测所获得的地表信息对其进行拟合得到。即统计不同距离间的协方差，选择一种合适的协方差函数，利用最小二乘估计拟合相应的参数值，最终确定协方差函数表达式。

常用的协方差函数有如下几种，其中C表示协方差，它仅与数据点之间的距离d有关，C0为信号方差。

1)高斯(Gauss)函数为

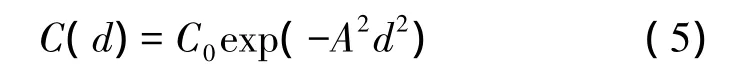
式中，A2为待定参数。

2)希尔方纳(Hirvonen)协方差函数为

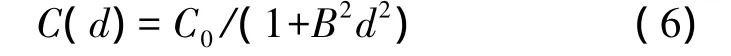
式中，B2为待定参数。

3)指数函数为

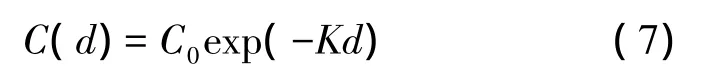
式中，K为待定参数。

2.各向异性协方差函数的拟合

在常规的协方差函数拟合过程中，常将随机信号视为各向同性的二阶宽平稳随机过程，然而各向异性特征更具有普遍性。通过对各个方向上的变异函数进行研究，可以显示出随机函数各种各向异性的性质。各向异性是指区域化随机变量在各个不同方向上的性质各不相同。根据性质的不同，各向异性又可分为几何各向异性和带状各向异性两类［26］。为简单起见，本文仅讨论几何各向异性。几何各向异性是指区域化变量在不同方向上具有相同的变异程度但具有不同的连续性，即不同方向的变异函数基台值相同而变程不同，如图2所示。

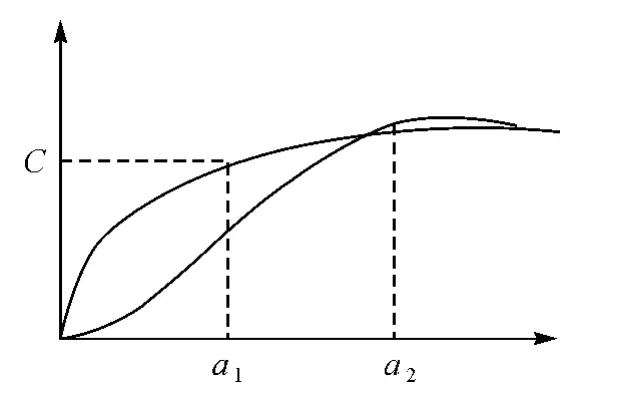
图2 几何各向异性

通常不同方向上变异性之差可以通过变程之比表示

式(8)意味着a2方向上距离为h的两点间的平均变异程度与a1方向上距离为kh的两点间的平均变异程度相同，即γa2(h)=γa1(kh)。

显然，若a1=a2，则表明随机向量各向同性，其对应的方向变程图为圆;若a1≠a2，则随机向量各向异性，其方向变程图可视为椭圆(如图3所示)。

为了将具有各向异性的随机向量转换成各向同性来处理，一个简单的办法是先通过旋转，使其方向与椭圆轴向重合;然后通过伸缩处理，即可获取具有相同统计特性的随机向量，如图4、图5所示。

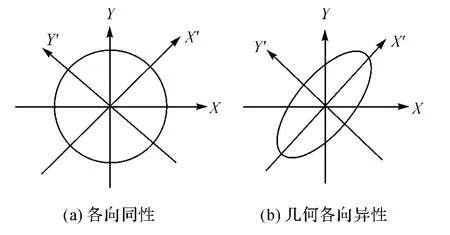
图3 方向—变程图

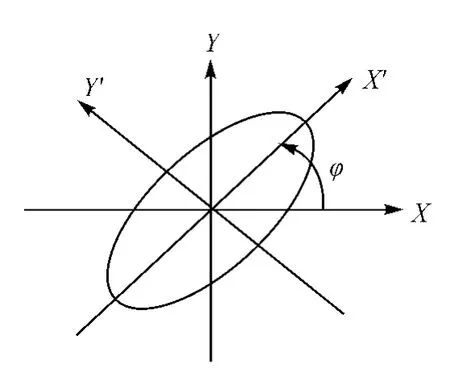
图4 旋转变换

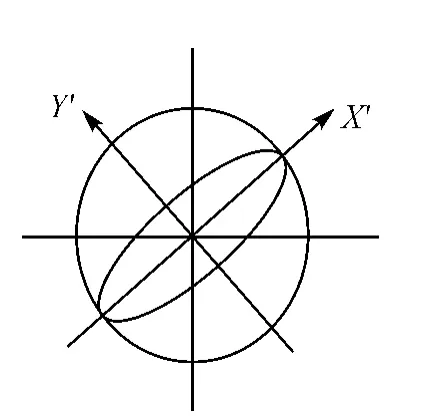
图5 伸缩变换

因此，在实际计算过程中，首先须根据已测信息，统计计算随机向量的椭圆三参数(即旋转角度φ、主轴长度amax与次轴长度amin)，以及主次轴长度比值 k=amax/amin。

其次通过旋转矩阵将坐标轴旋转角度φ，使其与椭圆轴相重合，旋转变换矩阵为

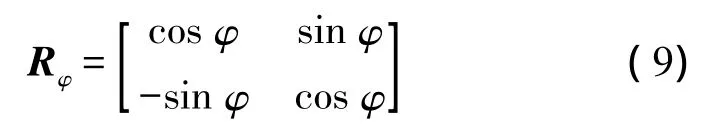
然后进行伸缩变换，将椭圆变换为半径等于椭圆长半轴的圆，其伸缩变换矩阵为

最后，逆旋转－φ角，恢复原来坐标方向，其旋转变换矩阵为

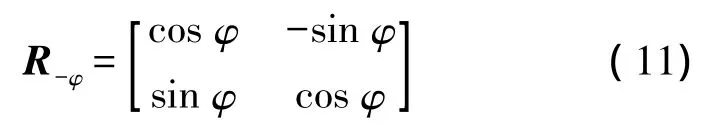
经过3次坐标变换，最后的坐标为

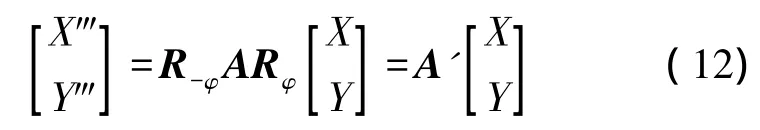
其中

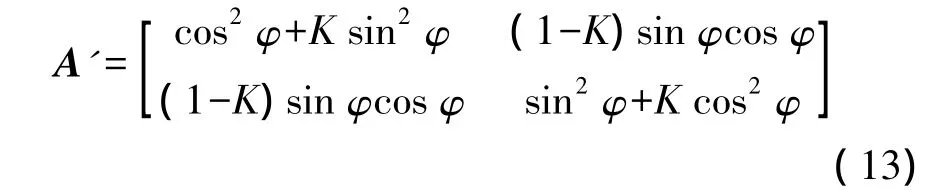
经式(12)的线性变换，即可将随机向量由几何各向异性转化为各向同性。于是可按各向同性的随机向量进一步计算处理。

四、基于各向异性的自适应拟合推估

基于各向异性的协方差函数能够较好地顾及随机向量的统计特性，由此拟合得到的协方差函数能够更加合理地表达向量间的相关性，但难以保证与观测噪声具有相同的单位权方差因子。因此为了协调随机信号与观测噪声对拟合推估解的影响，杨元喜［22-23］等提出了自适应拟合推估。其基本思想是通过引入自适应因子来平衡两者的贡献。

假设拟合推估函数模型为

式中，A、B为系数矩阵;L为观测向量;X为非随机参数向量;Y为随机信号向量，包括已测点信号S和未测点信号S'，即Y=[S S']T;Δ为观测噪声。

按照自适应拟合推估准则

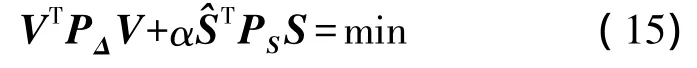
即可获得

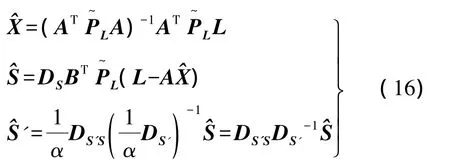
式中，V为误差向量;S为信号向量;PΔ和PS分别为V和S的权阵;α(0≤α≤1)为自适应因子;DΔ为观测值协因数阵;DS为随机信号协方差(BDSBT+αDΔ)－1。自适应因子 α 可通过方差比进行构建，即，其中随机信号协方差因子估计值和观测噪声协方差因子估计值可应用常用的方差分量估计(如Helmert方差分量估计、最大似然方差分量估计等)进行计算得到。

五、实例验证

为了验证基于各向异性自适应拟合推估的有效性，本文以某区域的部分地表形变监测信息(如图6所示)为试验数据，随机设置一系列缺失数据(如图7所示)作为检核数据。拟合推估计算中倾向性参数A、X采用二次多项式模型f=a0+a1x+a2y+a3xy+a4x2+a5y2，随机信号的协方差函数采用Gauss函数;并在不同的先验观测噪声(σ0=0.1，1，10)下，分别采用基于各向同性与各向异性的常规拟合推估方法与自适应拟合推估方法对试验数据进行处理。计算结果通过已测信号点的残差均方根误差和检核点不符值均方根误差来体现。

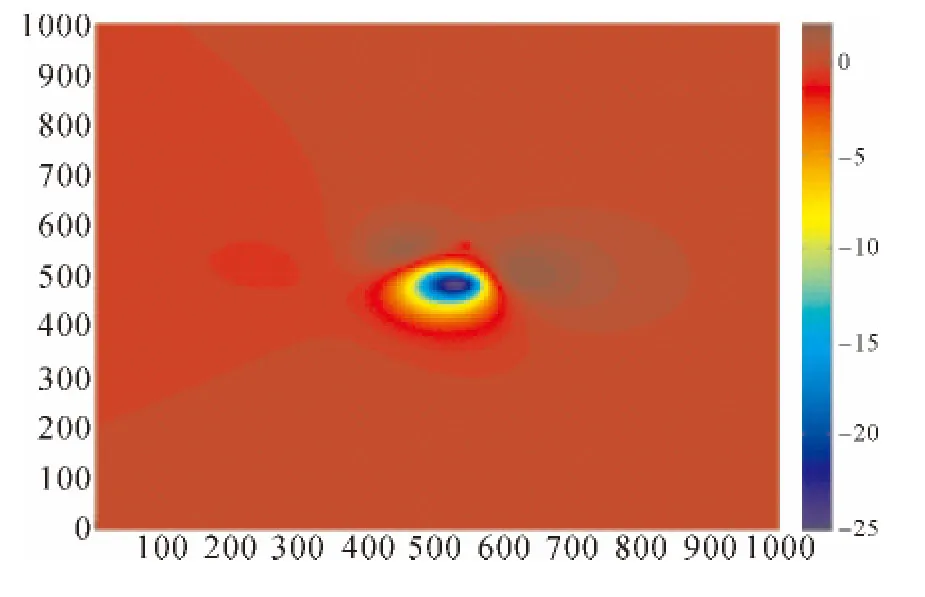
图6 试验数据

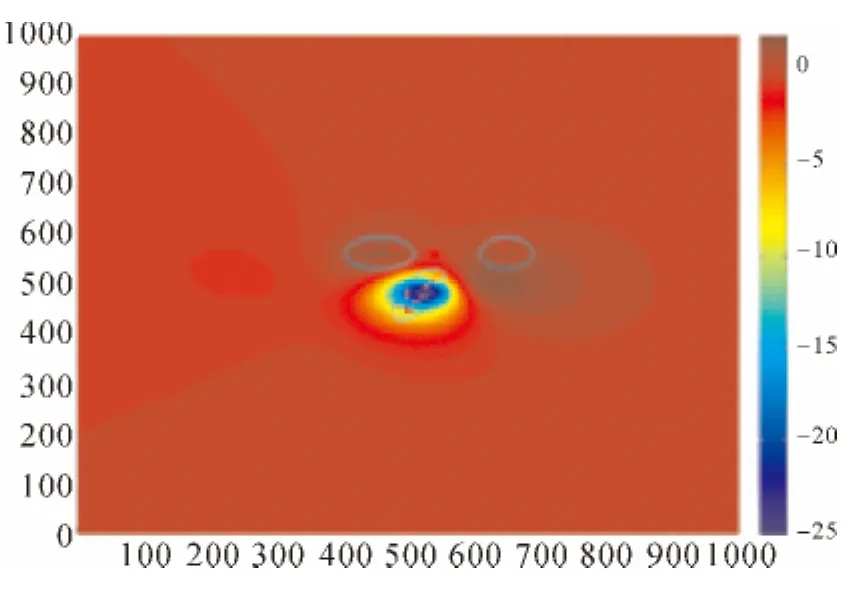
图7 缺失数据

计算结果见表1。

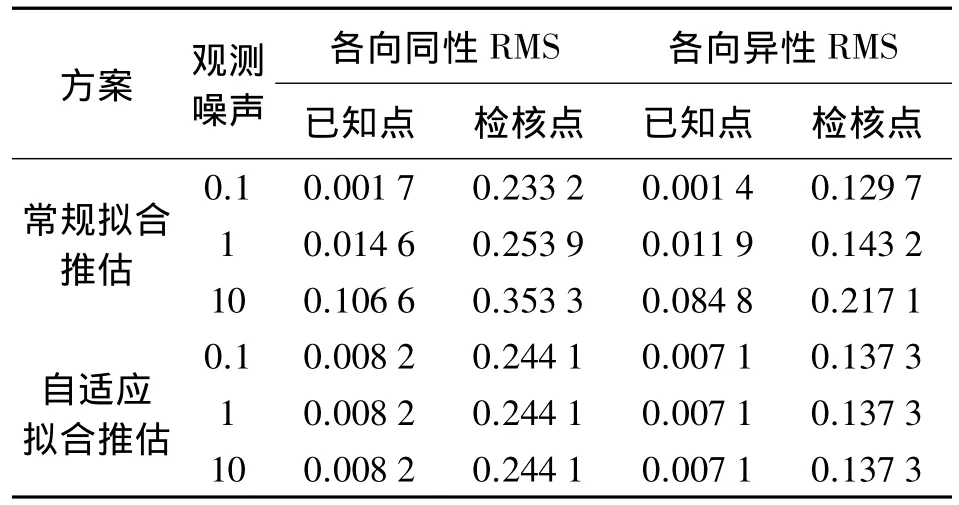
表1 各方案均方根误差计算结果

分析上述计算结果，可以发现:

1)基于各向同性与各向异性的常规拟合推估方法与自适应拟合推估方法都取得了较好的拟合效果，表明拟合推估方法在缺失数据拟合应用中具有可行性。

2)相比于各向同性的拟合推估，基于各向异性的拟合推估方法内部符合精度和外部检核精度均有不同程度的提高，表明基于各向异性的协方差矩阵能够更加合理地刻画随机向量的空间特性，从而具有更高的拟合填补精度。

3)正常拟合推估方法已测点与检核点推估解受观测噪声初始方差影响严重，而自适应拟合推估法则不受观测噪声初始方差的影响，表明通过自适应因子的引入，合理地调节了观测噪声与信号之间的权比，进而保证两者协方差矩阵的协调一致。

六、结束语

由于受各种因素限制，InSAR数据往往存在缺失，因此需要对缺失数据进行填补拟合。拟合推估方法既能较好地反映其空间分布规律，又能充分利用地表信息的空间相关特性，因此比较适合于缺失数据的拟合与推估。自适应拟合方法通过自适应因子的引入，保证了信号向量先验协方差矩阵与观测向量协方差矩阵的协调一致，进而平衡了两者的贡献。

此外，InSAR作为地表形变监测的重要手段，其数据信息不仅存在一定的空间分布规律，往往还存在局部变异性，呈现出各向异性的特点。基于各向异性的拟合推估方法利用变异函数可透过随机性反映区域化变量结构性的特点，先采用变异函数对形变信息进行各向异性研究，更好地对空间形变信息进行分析，将各向异性转化为各向同性后，再利用拟合推估方法进行拟合。这种方法充分考虑到地表形变监测信息的结构性与随机性，较常规拟合推估可以更好地对数据进行拟合，提高拟合精度。

此方法仅针对较为简单的几何各向异性进行研究，对于更为复杂的各向异性将在后续进行更为深入的研究。此外，拟合推估中协方差函数表达式的选择也十分关键，其选择也将直接影响拟合结果的可靠性。

［1］魏玉明.抗差最小二乘配置在重复重力测量数据分析中的应用［D］.西安:长安大学，2007.

［2］夏哲仁，林丽.局部重力异常协方差函数逼近［J］.测绘学报，1995，24(1):23-27.

［3］杨元喜，刘长建.重力异常的拟合推估迭代解算模型及算法［J］.地震学报，1996，18(4):475-479.

［4］章传银，丁剑，晁定波.局部重力场最小二乘配置通用表示技术［J］.武汉大学学报:信息科学版，2007，32(5):431-434.

［5］杨凤芸，张旭东.采用抗差推估法剔除GPS高程数据粗差［J］.测绘通报，2005(10):9-11.

［6］王增利，黄腾，邓标.基于二次曲面的拟合推估法在GPS高程测量中的应用［J］.测绘工程，2009，18(1):50-52.

［7］许双安.最小二乘配置和普通Kriging法在GPS高程转换中的应用［J］.测绘地理信息，2012，37(6):64-67.

［8］李冲，李建成，瞿伟.基于移动原理的拟合推估模型建立区域地壳运动速率场［J］.大地测量与地球动力学，2012，32(5):33-36.

［9］江在森，刘经南.应用最小二乘配置建立地壳运动速度场与应变场的方法［J］.地球物理学报，2010，53(5):1109-1117.

［10］曾安敏，刘光明，秦显平，等.应用拟合推估法建立我国大陆地壳水平运动速度场的研究［J］.测绘通报，2012(S0):11-15.

［11］张菊清，杨元喜，张亮.附有限制条件的拟合推估模型及其在地图数字化误差纠正中的应用［J］.大地测量与地球动力学，2008，28(5):91-95.

［12］张亮.抗差最小二乘配置在数字化地图几何纠正中的应用讨论［J］.测绘与空间地理信息，2008，31(2):145-148.

［13］曾安敏.基于拟合推估的1980西安坐标系到 2000国家坐标系的变换［J］.大地测量与地球动力学，2008，28(5):125-128.

［14］曾安敏，张菊清.基于拟合推估两步极小解法的地图坐标变换［J］.大地测量与地球动力学，2008，28(1):81-84.

［15］刘念，胡荣明.协方差函数的待定参数对最小二乘拟合推估精度的影响［J］.西安科技学院学报，2001，21(1):61-64.

［16］刘念.协方差函数的抗差拟合［J］.测绘科学，2001，26(3):25-28.

［17］文汉江.最小二乘配置法中局部协方差函数的计算［J］.测绘科学，2000，25(3):37-39.

［18］刘敏，王昆，邓凯亮，等.最小二乘配置中两种局部协方差函数的比较［J］.海洋测绘，2013，33(2):16-19.

［19］金保平，岳东杰，李成仁.基于遗传规划的协方差函数计算及其在GPS高程拟合中的应用［J］.测绘科学技术学报，2012，29(1):16-19.

［20］杨元喜，张菊清，张亮.基于方差分量估计的拟合推估及其在GIS误差纠正的应用［J］.测绘学报，2008，37(2):152-157.

［21］张菊清，张亮.基于Helmert方差分量估计的拟合推估法及其在地图数字化误差纠正中的应用［J］.测绘通报，2008(2):35-37，51.

［22］YANG Y X，XU TH.An Adaptive Kalman Filter Based on Sage Windowing Weights and Variance Components［J］.The Journal of Navigation，2003，56(2):231-240.

［23］杨元喜，曾安敏，吴富梅.基于欧拉矢量的中国大陆地壳水平运动自适应拟合推估模型［J］.中国科学:地球科学，2011，41(8):1116-1125.

［24］KNOSPE S，JÓNSSÓN S.Covariance Estimation for dIn-SAR Surface Deformation Measurements in the Presence of Anisotropic Atmospheric Noise［J］.IEEE Transactions on Geoscience and Remote Sensing，2010，48(4):2057-2062.

［25］程勖，杨毅恒，丁建华，等.变异函数在异常空间插值中的应用［J］.世界地质，2007，26(3):298-303.

［26］孙洪泉.地质统计学及其应用［M］.徐州:中国矿业大学出版社，1990.

［27］侯景儒.实用地质统计学［M］.北京:地质出版社，1998.

［28］MORITZ H.Statistical Foundations of Collocation［J］.Bollettino di Geodesia e ScienzeAffini，1980(2):131-150.