利用伸缩变换求解直线与椭圆相切问题初探

●钟顺荣(云和中学浙江云和323600)

利用伸缩变换求解直线与椭圆相切问题初探

●钟顺荣(云和中学浙江云和323600)

1 问题提出

1)已知直线l的斜率为k，用a，b，k表示点P的坐标;

2)若过原点O的直线l1与l垂直，证明:点P到直线l1距离的最大值为a-b.

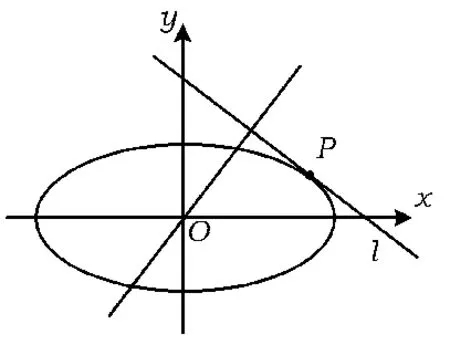
图1

(2014年浙江省数学高考理科试题第21题)

直线和圆锥曲线位置关系问题解决策略主要有5个步骤:“设”(点的坐标、直线、曲线方程)，“联”(联立方程组)，“消”(消去或得到一元二次方程)，“用”(运用韦达定理、中点坐标公式、弦长公式等)，“判”(运用判别式检验、求参数的值或缩小参数的取值范围).利用这种常规思路，在第1)小题的求解中，可假设直线l:y=kx+m(其中k＜ 0)，并与椭圆方程联立，消去y得到关于x的一元二次方程，再结合Δ=0求解出点P的横坐标，进而得到点P的纵坐标.

由于求解过程中涉及到直线与圆锥曲线联立、消元等问题，计算量较大.若能避开直线与圆锥曲线联立，便可达到简化运算的目的.

2 源于教材的知识再探

人教A版选修1-1第34页:在圆x2+y2=4上任取一点P，过点P作x轴的垂线段PD，D为垂足.当点P在圆上运动时，线段PD的中点M的轨迹是什么?

问题揭示了圆与椭圆之间的内在关系，即通过点坐标的伸缩变换，可以在平面直角坐标系中实现椭圆与圆的互换.类似的伸缩变换思想在三角函数变换中也有.

事实上，设M(x，y)是平面直角坐标系中任意一点，在变换φ:的作用下，点M(x，y)对应点M'(x'，y')，称φ为平面直角坐标系中的伸缩变换.同时，由方程确定的伸缩变换具有下列性质:

1)点M(x，y)的像为点M'(x'，y')，斜率是k的直线的像为斜率是的直线;

2)变换后共线3个点的2条线段的比值和变换前的比值一样;

3)设封闭曲线C围成的面积为S，C的像C'所围成的面积为S'，则S'=mnS;

4)2条曲线C1，C2有公共点M，则曲线C1，C2的像C1'，C2'必有公共点M'，且M'是M的像;

5)2条曲线C1，C2在点M处相切，则曲线C1，C2的像C1'，C2'在点M的像M'处也相切.

3 利用伸缩变换解决直线与椭圆相切问题初探

基于上述伸缩变换的性质，可以用圆的性质去探索椭圆的相关性质，同时也可以将椭圆的有关问题转化成圆的问题去解决，借助圆的一些特性来简化运算.现以直线与椭圆相切问题举例如下:

3.1 过椭圆上一点的直线与椭圆相切问题

例1第1)小题的伸缩变换解法如下:

图2

解如图2，设切点为P(x0，y0)，在伸缩变换作用下，椭圆变换为圆x'2+ y'2=1，椭圆上的点P(x0，y0)变换为圆上的点，过点P的切线l变换为过点P'的切线l'，且由点P'在x'2+y'2=1圆上得

由O'P'⊥l'得

1)求椭圆的方程;

2)设F1，F2分别为椭圆的焦点，M为线段AF2的中点，求证:∠ATM=∠AF1T.

图3

再思考:已知∠TAF1=∠MAT，要证明的是∠ATM=∠AF1T，于是△TAF1∽△MAT，从而转为求相关边长的比值，但在椭圆中直接求|AT|较复杂，借助伸缩变换成圆后，发现，由性质2)知必为，从而轻松求出|AT|.

例2的伸缩变换解法如下:

图4

又∠TAF1=∠MAT，从而△TAF1∽△MAT，得∠ATM=∠AF1T.

过椭圆上一点的直线与椭圆相切问题经过伸缩变换后转化成过圆上一点的直线与圆相切问题，再利用圆心与切点的连线和切线垂直的特性，借助2条直线斜率之积等于-1或圆心到切线距离为半径求解，巧妙避开了解析几何中的联立消元.

3.2 过椭圆外一点的直线与椭圆相切问题

1)求椭圆C的标准方程;

2)若动点P(x0，y0)为椭圆外一点，且点P到椭圆C的2条切线相互垂直，求点P的轨迹方程.

(2014年广东省数学高考理科试题第20题)

思路1设切线方程为y-y0=k(x-x0)，并与椭圆方程联立，由Δ=0得到关于k的一元二次方程，再利用韦达定理得到2条切线斜率kPA·kPB的关系，结合kPA·kPB=-1求解(要注意对切线斜率是否存在进行讨论).

上面2种思路都需要联立直线和椭圆方程，计算较为复杂，可借助伸缩变换重新整理如下:

图5

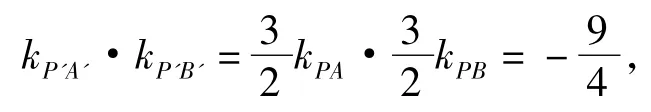
直线P'A'，P'B'与圆O'相切.设过点P的圆的切线方程为

根据韦达定理知

故点P的轨迹方程为x2+y2=13.

将例3中的椭圆推广到一般情况可以得到如下命题(证明同上):

例3变式若P是直线4x+3y-18=0上的动点，PA，PB是椭圆C的2条切线，A，B为切点，求四边形面积PAOB的最小值.

例3变式的伸缩变换解法如下:

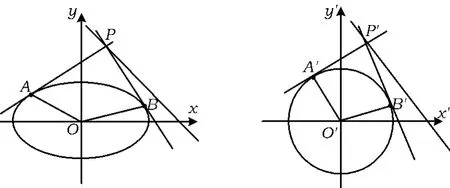
图6

易知当O'P'⊥l'时，|O'P'|有最小值，于是

由性质3)得

用常规方法求解与椭圆相关的三角形面积问题时计算量很大.若另辟蹊径，通过伸缩变换转化为与圆相关的三角形面积，则会起到事半功倍之效.

转化思想是中学数学中最基本的思想方法之一，体现为化抽象为具体，化未知为已知，化复杂为简单.基于圆的特性及椭圆和圆的内在联系，可以利用伸缩变换将椭圆变换为单位圆，把直线与椭圆的位置关系问题转化为直线与圆的位置关系问题，从而实现“椭圆问题圆解决”，避开解析几何繁琐的运算.同时，椭圆的性质也可以类比圆的性质学习.用联系的观点学习数学，可以使孤立的知识点统一起来，这对于我们构建知识网络、提升数学思维有着重要意义.

［1］刘殿光.利用压缩变换研究椭圆［J］.中学生数学，2003(1):33.

［2］汤敬鹏.利用仿射变换解决与椭圆有关的高考试题［J］.数学通讯，2010(4):44.