“老”的求和问题“新”的求解视野——对错位相减法的持续思考

●郑燕平(金华市第一中学浙江金华321015)

“老”的求和问题“新”的求解视野
——对错位相减法的持续思考

●郑燕平(金华市第一中学浙江金华321015)

众所周知，对于通项是anbn(其中{an}是等差数列，{bn}是等比数列)形式的数列都可以采用错位相减法.这一方法是推导等比数列前n项和公式的推广，其精髓在于通过错位将同次幂的项相减，使得这些项的系数相等，从而转化为局部的等比数列求和来解决问题.对于这块内容的学习，学生接受知识容易但操作起来正确率不高.笔者一直在思考有没有更好的方法来解决这类问题?现笔者将一些想法整理成文，以飨读者，有不当之处，请批评指正.

新视角1将数列的项进行重新整理

例1求数列1，1+2，1+2+22，…，1+2+ 22+…+2n-1的前n项和Sn.

分析一般的解法是将该数列的通项求出

再利用分组求和法求出

换个角度我们可以将该数列的前n项和Sn分成n个1，n-1个2，n-2个3，……，1个2n-1，于是

这不是通项是anbn(其中{an}是等差数列，{bn}是等比数列)的形式吗?即可以反其道而行之，将适用错位相减法的数列转化为例1所示的数列形式，就成功避开了错位相减法这个拦路虎!不妨一试:

例2求数列{n·2n}前n项和Sn.

利用分组求和法，可得

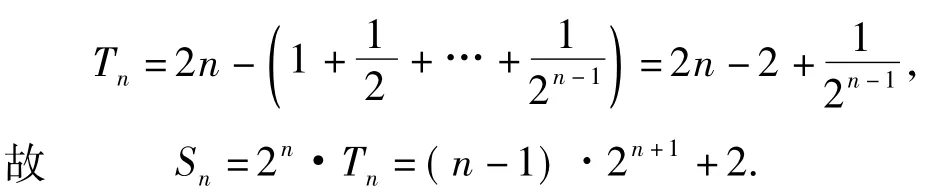
评注笔者发现这一思想不仅适用于求形如数列{anbn}(其中{an}是等差数列，{bn}是等比数列)的前n项和问题，而且还可以求一些等差乘以其他数列为通项的求和问题，如:

例3求和:Sn=12+22+32+…+n2.

分析这是正整数的前n项和，很多教材上都是先猜想再用数学归纳法证明.我们可将该数列重新写成数列n，n+n-1，…，n+n-1+…+n-k+ 1，…，n+n-1+n-2+…+2+1，其通项为

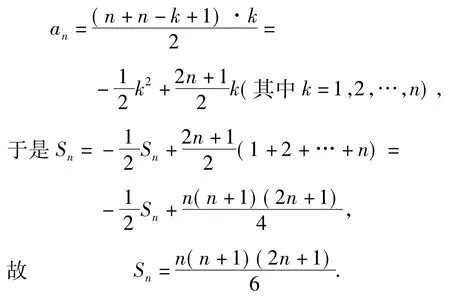
新视角2利用待定系数法

分析求形如an+1=pan+g(n)(其中p是常数)的数列通项问题，主要思想是根据g(n)的形式，利用待定系数法构造相应形式的递推关系，从而化归为等比数列的问题.这里g(n)=2n-1是一次函数，故可构造通项为an-(An+B)形式的数列.

设an-(An+B)=3{an-1-［A(n-1)+B］}，则

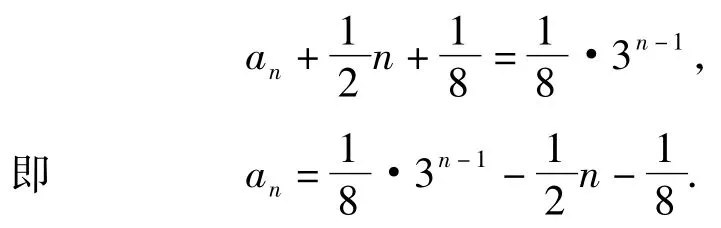
只需将上面的方法作一个类比，就可以不用错位相减法来求数列{anbn}(其中{an}是等差数列，{bn}是等比数列)的和.具体类比如下:在求cn= 3·2n的前n项和Sn时，可以将其视为等比数列的和;也可以这样思考:将cn=3·2n写成cn=λ· 2n+1-λ·2n，易知λ=3，那么就可以用裂项相消的思想来求和:

接着，自然会想到当等比数列不是乘以常数而是乘以等差数列时，能否如此操作呢?下面举例说明:

例5求数列cn=(2n+3)·3n的前n项和Sn.

分析设cn=(An+B)·3n+1-［A(n-1)+ B］·3n，则

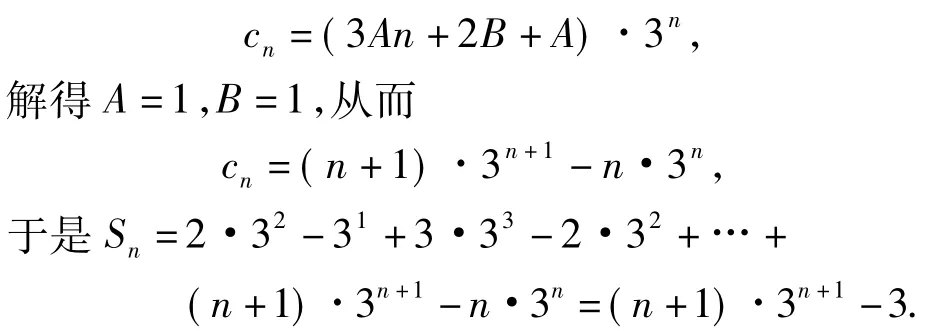
评注这里巧妙地利用待定系数，将形如数列{anbn}(其中{an}是等差数列，{bn}是等比数列)的和转化为裂项相消求和问题.笔者发现这一思想不仅适用于求形如数列{anbn}(其中{an}是等差数列，{bn}是等比数列)的前n项和问题，还可以应用于其他形式的数列求和.下面以文献［1］中提出的问题为例进行说明:

例6已知数列an=(n2+n)·3n，求Sn.

分析文献［1］利用2次错位相减法才解决这一问题，用本文的思想就非常容易.因为这里等比数列{3n}前乘的是关于n的二次式，所以可构造关于n的二次式的裂项式子.

由此可见，利用待定系数法可将形如an= f(n)·bn(其中{bn}是等比数列)的数列求和问题转化成裂项相消求和的问题.

新视角3利用导数知识

幂函数的导数(xn)'=nxn-1，即等差乘以等比的结构.循着这一想法，我们来试验一下:

例7求f(x)=x0+2x1+3x2+…+nxn-1.

利用这个结论可解决本文例2的问题:即当x=2时，

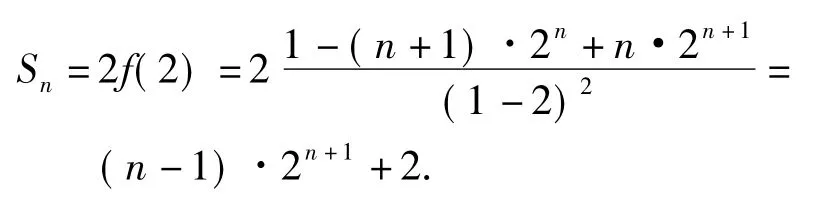
数学充满了奥妙，很多数学思想方法都是相通的.只要我们有一双发现的眼睛，挖掘各种方法的内涵，找准问题解决的关键，就能将方法进行有效地迁移，收到意想不到的效果.或许这就是数学的魅力所在吧!

［1］吕建恒，王微.一类数列求和的方法［J］.中学数学，2006(12):19.

［2］李志臣.“待定系数法”解递推数列［J］.中学数学教学参考，2006(12):29-30.