警惕概率题的等可能性

●吴彤(盐城市教育局教科院江苏盐城224000)

警惕概率题的等可能性

●吴彤(盐城市教育局教科院江苏盐城224000)

1 解法疑问

最近，笔者到某校检查高三数学教学工作时，听了一节试卷评讲课.课堂上，任课教师甲评讲了下面这道概率题:

例1在十字路口的路边，有人在促销木糖醇口香糖，只听喇叭里喊道:木糖醇口香糖，10元钱3瓶，有8种口味供你选择(其中有一种为草莓口味).小明一看，只见一大堆瓶装口香糖堆在一起(假设各种口味的口香糖均超过3瓶，且每瓶价值均相同).

1)小明花10元钱买3瓶，请问小明共有多少种选择的可能性?

2)小明花10元钱买3瓶，售货员随便拿3瓶给小明，请列出有小明喜欢的草莓味口香糖瓶数ξ的分布列，并计算其数学期望.

对于第1)小题，教师甲着重分析了学生出错率较高的情况:若其中2瓶口味一样，通过分析得到2种处理方法:有种，或有种;若3瓶口味均不一样，有种;若3瓶口味一样，有8种.因此，小明共有56+56+8=120种选择.

对于第2)小题，容易得到ξ的取值为0，1，2，3.然后教师甲重点分析了下列4个概率值的运算:

这里的运算方法很简单，就是把ξ的每个取值的种数求出来，再除以所有种数120得出相应的概率，从而最终得到数学期望.这样求概率的方法是否妥当呢?

2 交流研讨

课后，笔者召集了该校高三数学备课组的全体成员，交流研讨高三数学教学的相关问题，上述概率题的解法也是研讨内容之一.通过研讨，笔者与该校高三数学教师对概率的理解和认识都有所提高，以下笔者把交流研讨的具体内容整理成文，供读者在教学中参考.

笔者:上节课，我听了教师甲的一节试卷评讲课，他评讲了试卷中的一道概率题(出示例1).其中第2)小题，教师甲是按照试卷提供的答案评讲的，我感觉这个解答好像有点问题，请大家谈谈自己的看法.

教师乙:第1)小题共有120种情况没有错，但在第2)小题中，能不能把120作为分母求概率是个问题.

教师甲:总共有120种情况，把ξ的每个取值的种数除以120不就得到对应的概率，怎么不能?

教师乙:问题是120种情况中的每种情况是否等可能?

教师丙:总共有120种情况，就是120种口味的选择，怎么不等可能?

此时，出现了教师之间的争论，大家你一言我一语，互不相让.该备课组共有18位教师，认为答案肯定没有问题的有5位，怀疑题目、答案有问题的有3位，其余教师(主要是年轻教师)未参与争论.

笔者:大家先静一静，我们暂且不谈这个概率题的正误，此题中有这样一个条件“假设各种口味的口香糖均超过3瓶，且每瓶价值均相同”，现把问题具体化“假设每种口味的口香糖均4瓶，”其他条件不变，这虽然有点不太符合生活中的实际情况(一大堆瓶装口香糖堆在一起，数量应该比较大)，但作为数学问题，看看能不能解答?

教师乙:第1)小题没有影响，但第2)小题就变成超几何分布了，分母应是，求得ξ的每个取值概率如下:

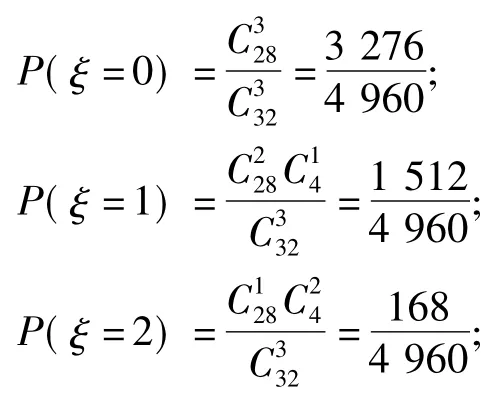
笔者:改编后的题目以及教师乙的解答，大家是否认同?

教师甲:这当然不错，但原来的问题是各种口味的口香糖瓶数不确定，这个概率题是不考虑瓶数的，它主要是针对不同口味而言.

笔者:现在还有个问题，一但确定了各种口味的口香糖瓶数，数学期望还不一定是.比如，有4种口味(包含草莓味)的口香糖各4瓶，另外4种口味的口香糖各5瓶，这时概率分布毫无疑问又要发生变化，数学期望.原题没有确定各种口味的口香糖瓶数，但现在确定了瓶数，概率分布与数学期望都发生变化，这是不是有点不符合道理?

教师乙:确定了瓶数后的问题是原问题的特殊情况，那么原问题就应该包括各种特殊情况，但事实上，不同特殊情况的概率分布与数学期望不同，这说明不能把原问题作为一个统一性的问题.

教师乙的这几句话击中了该问题的“要害”.

笔者:教师乙的分析有一定的道理.刚才的2个特殊例子，口香糖的瓶数不够多，有点近似于生活中的摸球中奖问题，应该用超几何分布完成;符合实际生活情况的应该是当每种口味的口香糖瓶数都比较多，原题中“一大堆瓶装口香糖堆在一起”，数量应该比较大，设计成二项分布的问题比较合理，如“每种口味的口香糖瓶数都足够多，任取一瓶，每种口味取到的可能性都相同”，这时，每次取到草莓味口香糖的概率都是，从而概率分布为

教师甲:我有点明白了，这个概率问题应该是2个模型之一，用二项分布完成，强调的是“任取一瓶，每种口味取到的可能性都相同，取到草莓味的概率是，取不到草莓味的概率是”;用超几何分布完成，应该是从总数中任取3瓶，取到的每种情况才等可能.

笔者:是的，原解答把120作分母求概率，必须要求120种情况中的每一种情况都等可能才行.我们再用刚才的例子“假设每种口味的口香糖均为4瓶”来验证等可能性:若3瓶口味均不一样，共有56种搭配，取3瓶口味均不一样的概率是

3 再思考

这次讨论，先是从感觉解法有点问题，到用特殊例子检验，再到理论分析，笔者收获不小，认识了等可能性对求概率的重要性.事后，笔者又翻看了有关教材，对中学阶段的几种概型作了研究和思考:

在苏教版必修3中，学习了古典概型，如果一次试验的等可能基本事件有n个，事件A包含了其中m个等可能事件，那么事件A发生的概率为.可见，求古典概型问题的概率需要注意等可能性;随后，又学习了几何概型，教材中强调了“每个基本事件可以视为从区域D内随机取一点，区域D内的每一个点被取到的机会都一样”，虽然这里没有用“等可能”叙述，但“每一个点被取到的机会都一样”就是指“每一个点被等可能地取到”，因此，求几何概型问题的概率蕴含了等可能性.