探月返回器稀薄气体热化学非平衡特性数值模拟

梁 杰,李志辉,杜波强,方 明

(中国空气动力研究与发展中心超高速所，绵阳621000)

探月返回器稀薄气体热化学非平衡特性数值模拟

梁 杰,李志辉∗,杜波强,方 明

(中国空气动力研究与发展中心超高速所，绵阳621000)

通过发展直角/非结构混合网格下，适于复杂返回器含内能激发的五组元热化学非平衡稀薄气体直接模拟蒙特卡洛(DSMC)方法，数值模拟了钝体返回器稀薄流区7.5 km/s和10.6 km/s再入速度下的非平衡流场特性和对物面气动力/热分布的影响。计算结果表明在月球返回速度下稀薄过渡流区存在着强烈的热化学非平衡，近连续滑移区仅在激波层区域存在着较大的平动、转动和振动非平衡度，而在高稀薄流区，热力学非平衡遍布绕流物体四周，包括整个压缩区和尾迹区。高温真实气体效应对表面热环境影响显著，对表面压力和摩擦力的影响相对较弱。计算结果显示探月返回器再入绕流过程100 km飞行高度仍需要考虑热化学非平衡的影响。

探月返回器；稀薄流域；热化学非平衡；DSMC方法；数值模拟

1 引言

月球探测返回舱是月球样品的承载和运输工具，以近第二宇宙速度、半弹道跳跃式再入大气层，其间经历自由分子流、稀薄过渡流和连续流等多个流动区域，其再入飞行过程的静动态气动特性和热环境都具有新的特点。当返回舱以极高的速度再入大气层时，由于激波和粘性的作用会产生严重的气动加热，使返回器表面及其周围流场高温气体发生复杂的物理、化学变化，这个过程伴随着气体分子的离解和电离，同时也会出现分子的振动激发、束缚电子的激发和辐射热，壁面的化学反应也可能发生[1-2]。在高空稀薄气体流域，由于气体的密度低，粒子之间的碰撞频率降低，超高速返回器绕流流场中气体分子的平动温度、转动温度和振动温度处于高度的非平衡状态，激波后高温气体发生化学反应的弛豫时间远大于流动的特征时间，因而在返回器的绕流中会出现严重的热化学非平衡现象[3-4]。这些气体流动现象会造成流动结构的显著变化，并对返回器的气动特性产生重要影响。详细了解稀薄过渡流区的热化学非平衡特性以及对返回器表面特性的影响对高超声速返回器的设计非常重要，但地面试验设备很难模拟低密度环境下的高焓真实气体效应并且试验费用昂贵。随着高性能计算机的发展以及不断更新的物理化学模型，使大规模并行计算成为研究稀薄过渡流区热化学非平衡效应的主要手段，基于气体分子速度分布函数为Maxwell平衡态分布概念的连续流气体动力学计算理论，如求解NS方程，已经不再适用于稀薄气体流域的模拟，取而代之的是基于分子气体动力学的直接模拟蒙特卡洛(DSMC)方法[5]，通过模拟分子在计算区域内运动、相互之间碰撞以及与固体表面之间的相互作用来实现真实气体流动的模拟。本文采用流场直角/表面非结构混合网格结构的DSMC方法(已在文献[6，7]验证了该算法可靠性)，发展适于复杂返回器含内能激发的五组元热化学非平衡模拟技术，研究分析钝体返回器在稀薄过渡流区不同再入速度下的非平衡流场特性和对物面气动力/热参数分布的影响规律。

2 模拟热化学非平衡流动的DSMC方法

2.1 依赖于温度的转动和振动松弛模型

式中，ζt、ζr和ζv分别是分子平动、转动和振动自由度。直到二十世纪九十年代DSMC方法中的转动和振动碰撞数都取为常数(Zr＝5，Zv＝50)[10]。根据分子运动论可知，同一密度条件下的气体流动，温度越高，分子间的碰撞越频繁，松弛的过程也就越快，因此松弛速率总是与温度有关的函数。Parker[11]给出了连续流气体分子转动松弛所需要的碰撞数ZCr与气体温度之间的关系表达式如式(2):

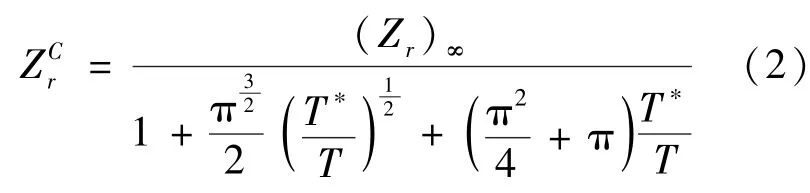
式中，T∗是气体分子作用势的特征温度，(Zr)∞是实验测定的极限值。

连续流的振动松弛碰撞数定义为式(3):

式中，τc为分子平均碰撞时间，τMW为振动松驰时间，τP为高温修正项。

由Landau-Teller理论结果给出式(4):

其中，p＝nkT。

Millikan和White[12]在高温激波管内通过干涉仪观测了气体分子振动松驰过程，在104K的温度范围内，给出了如式(5)所示拟合参数:

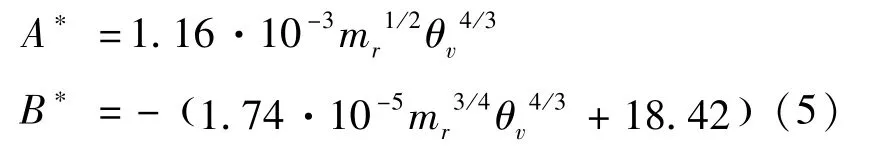
其中，mr为分子折合质量，θv是振动特征温度。Park[13]给出了高温修正的τP为式(6):

式中，n是数密度，σv是分子振动碰撞截面(＝10－20m2)，是分子平均热运动速度。

2.2 化学反应模型及非弹性碰撞模拟策略

通常反应速率常数可以写成式(7)所示的Arrhenius方程形式:

式中，Ea是反应中需要的活化能，k是Boltzmann常数，Λ和η是常数，由试验定出。

化学反应几率可以推导为式(8)所示表达式[5]:

式中，ε是对称因子，对于不同类分子ε＝1，对同类分子ε＝2。为碰撞分子的平均内自由度，ωAB为碰撞对的粘性温度指数。当碰撞中的总碰撞能量Ec＞Ea时，反应截面σR与总碰撞截面σT的比值就是反应发生的概率，这种化学反应模型也称为TCE(Total Collision Energy)模型。

在DSMC模拟过程中为简化碰撞算法，假设非弹性碰撞的化学反应过程和内能交换是相互独立的事件。由于碰撞分子发生化学反应的几率在所有非弹性碰撞事件中是最低的，所以首先判断其是否发生化学反应。离解反应、交换反应等不同的化学反应过程在满足反应几率的条件下都有可能发生。在无法获知反应分子遵循何种反应轨迹生成新的反应生成物时，可以假定每种反应过程都是独立的。对所有可能发生化学反应的几率求和得到总的反应几率，如果Pr＞ Rf，碰撞分子发生化学反应[14]。具体发生的是何种反应类型，则同样根据几率Pir/Pr与随机数Rf的比较来选取，然后按照相应的化学反应类型产生新的生成物(分子或原子)。

对于不发生化学反应的碰撞分子，即Rf＞Pr时，则根据分子振动抽样概率，判断是否发生振动自由度的激发；对于未发生振动激发的分子，再根据分子转动抽样概率，判断是否发生转动自由度的激发；对于发生内自由度激发的分子，按相应的能量交换模型进行能量的再分配，否则分子按弹性碰撞处理。

本文模拟了五组元(O2，N2，O，N，NO)气体的离解反应和交换反应，未考虑电离的发生。

2.3 不同温度模式的非平衡度定义

为研究航天器再入高超声速绕流稀薄气体环境下，分子内能激发致平动、转动和振动非平衡的程度，本文定义变量η作为不同温度模式非平衡程度的度量参数。对于平动温度的非平衡度用三个分量来表示，其定义为式(9):

其中，Tt是分子的平动温度，(Tt)i，i＝x，y，z分别是三个方向的速度分量定义的平动温度。分别定义转动温度非平衡度和振动温度非平衡度为式(10)、(11):

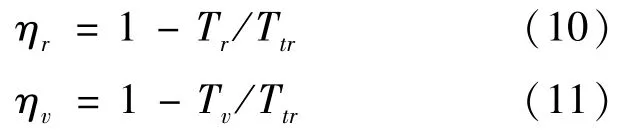
其中，Tr和Tv分别是转动温度、振动温度。

3 计算结果分析

本文选取类飞船返回舱的探月返回器外形作为研究对象，来流速度分别为 7.5 km/s和10.6 km/s，计算的高度范围为80～120 km(Kn数为0.0025～2.44)，攻角为－20°，壁面温度设置为500 K，采用完全漫反射模型，因不考虑侧滑角，仅计算对称的半个流场，计算中考虑了分子的转动、振动能量激发以及五组元空气的离解反应和交换反应。

图1、图2分别是来流速度7.5 km/s条件下80 km和100 km高度返回器绕流流场的平动温度、转动温度和振动温度沿中心流线的变化曲线。远前方气流在返回器的前方被激波压缩加热，吸收的能量首先供应给平动能，使平动温度迅速上升；随着分子碰撞松弛影响的进一步加剧，气体分子碰撞致内部能量迅速增加，分子转动和振动能态也相继激发。受壁面温度条件限制，最后平动、转动和振动温度在物面附近被强制平衡到壁面温度。由此可见，在激波和激波压缩层区域，平动温度、转动温度和振动温度之间较大程度的偏离，反映出气体流动呈现出强烈的热力学非平衡特征，这也是稀薄气体流域所特有的流动现象。随着气体稀薄程度的增大，来流气体密度降低，分子之间的碰撞频率减弱，分子转动和振动自由度的激发程度明显下降，引起转动温度和振动温度的迅速降低，导致平动温度与转动温度、振动温度之间差异增大、非平衡度增加。

图1 返回器再入80 km流场沿中心流线温度分布Fig.1 Temperature distribution around reentry capsule along central streamline at 80 km height

图2 返回器再入100 km流场沿中心流线温度分布Fig.2 Temperature distribution around reentry capsule along central streamline at 100 km height

从前面定义的不同温度模式的非平衡度，可以了解整个流场的热力学非平衡分布情况。图3、图4分别给出了来流速度7.5 km/s返回器再入80 km和100 km高度绕流流场的转动温度和振动温度非平衡度等值线分布。80 km的Kn数为0.0025，流动属于近连续滑移流区，图中显示出头部激波的压缩性非常强，激波层很薄，在流场的大部分区域都处于平衡态，热力学非平衡主要分布在激波层附近区域。返回器钝体前方激波压缩温度迅速上升引起严重的转动和振动非平衡，在后体激波层区域振动非平衡度仍然较高，并且分布的区域明显宽于转动非平衡度，主要是由于振动能激发相对较弱且滞后于转动能，振动温度与平动温度的偏离较大造成的。在100 km高度时已看不到明显的激波，而在返回器前部出现较强的气体压缩强扰动变化过程，边界层与强扰动激波压缩层相互融合，出现厚厚的强扰动激波过渡层，并且是随着绕流物体后部稀薄程度增加，激波层厚度也随之增大，变成了一个强扰动压缩过渡带。图4显示出在整个压缩区和尾迹区均存在较严重的转动和振动非平衡。同样，在80 km高度激波层区域由不同方向速度分量定义的平动温度本身也存在着较大的非平衡。

图3 返回器再入80 km流场转动（左）和振动（右）温度非平衡度等值线分布Fig.3 Nonequilibrium degree contours of rotational（left）and vibrational（right）temperature at 80 km height

图4 返回器再入100 km流场转动（左）和振动（右）温度非平衡度等值线分布Fig.4 Nonequilibrium degree contours of rotational（left）and vibrational（right）temperature at 100 km height

图5 是x方向和y方向的平动温度非平衡度分布，在头部脱体激波压缩最强的地方也是x方向速度变化最剧烈的位置，x方向的平动温度非平衡最强，而在沿返回器身部的脱体激波层区域，则是y方向的平动温度非平衡度最大。z方向的平动温度非平衡度在激波层区域从0.5～0.7之间变化。同时也看到，在后体尾迹膨胀区也有局部的平动非平衡。随着飞行高度的增加，平动温度非平衡区域不断扩大，到返回器再入100 km高度绕流流场，在整个压缩区域和尾迹区也都存在着较严重的平动温度非平衡。

图5 返回器再入80 km流场平动温度非平衡度等值线分布Fig.5 Nonequilibrium degree contours of translational temperature around reentry capsule at 80 km height

返回器在以超高速再入飞行时，双原子分子之间较高的碰撞能量不但会引起转动和振动自由度的激发，形成较强的热力学非平衡流动，还会发生一定程度的化学反应，生成新的化学组元。图6给出了返回器再入80 km高度、来流速度分别为7.5 km/s和10.6 km/s绕流流场中化学组元摩尔分数沿中心流线的变化情况，图中显示出返回器绕流流场存在较强的化学非平衡流动特征。在激波层区域，气体分子的高密度产生高碰撞率，使离解活化能较低的O2分子离解速率远大于N2的离解速率，在气流到达物面前，O2全部离解完毕。

N2分子在10.6 km/s的来流速度下大部分离解，使N原子的摩尔浓度接近了N2分子发生离解前的初始摩尔浓度，如图7分别展示了N2分子和N原子摩尔分数流场等值线分布，激波后的返回舱周围分布着大量的离解后的N原子，显示出强烈的化学非平衡效应。

图6 返回器再入80 km流场沿中心流线组元摩尔分数分布Fig.6 Mole fraction distribution of gas species around reentry capsule along central streamline at 80 km height

图7 返回器再入80 km和10.6 km/s速度下流场N2分子和N原子摩尔分数分布Fig.7 Mole fraction distribution of N2molecule and N atom around reentry capsule at 80 km height with 10.6 km/s velocity

对比图6(a)中N2分子在7.5 km/s来流速度下离解反应要弱得多，表明同一飞行高度，返回器以近第二宇宙速度10.6 km/s再入比第一宇宙速度7.5 km/s再入致流场呈现更加严重的热化学非平衡流动特征。在五个化学组元中NO的含量是最低的，并且是先上升再下降接近于零，说明发生交换反应生成NO的几率并不高，同时也表明生成的NO在靠近物面前也基本离解完毕。图8绘出返回器以10.6 km/s再入100 km高度飞行绕流流场沿中心流线组元摩尔分数分布曲线，与图6(b)对比看出，随着飞行高度由80 km增加到100 km，稀薄效应变得很严重，致使化学反应的强度不断减弱，但在 10.6 km/s的来流速度下，100 km高度仍有较强的化学反应发生。这与通常情况，返回器以第一宇宙速度7.5 km/s飞行绕流在100 km以上几乎不再有化学反应发生，形成鲜明的对比，预示未来我国发展的探月返回器再入绕流过程100 km以上就要考虑化学反应的发生为宜。因此不同的来流速度和来流密度条件下，发生离解反应和交换反应的程度以及生成新组元的分布规律有明显不同，对比图6、图8各组元在流场中的分布，同样发现来流初始条件对流场的化学非平衡特性以及组元分布有较大影响。

图8 返回器再入100 km流场沿中心流线组元摩尔分数分布（V＝10.6 km/s）Fig.8 Mole fraction distribution of gas species along central streamline at 100 km height（V＝10.6 km/s）

图9～11展示了不同高度、来流速度7.5 km/s时高温气体热化学非平衡效应对返回器子午面φ＝0°，180°沿x－方向不同位置气动力/热参数分布的影响，图中实线是计算中仅考虑N2和O2混合气体分子的转动能激发，定义为TR气体。而反应气体则是考虑了N2和O2混合气体分子的转动能和振动能激发以及化学反应。图9(a)显示出在80 km高度时TR气体计算的热流明显高于反应气体的热流，在驻点区域大一倍左右，说明高温气体热化学非平衡效应对返回器表面热环境有显著的影响，主要是考虑热化学反应真实气体分子能量有很大一部分因激发分子振动自由度与发生离解反应吸热，导致气体温度降低，物面温度梯度与热流下降。随着飞行高度的增加，无论是分子的振动激发还是化学反应都不断减弱，到100 km高度时两种气体计算结果表明，表面热流几乎是重合的(图9(b))。另外，热流分布也表明在－20°攻角下，最大热流位于肩部而不是驻点。化学反应对表面压力和摩檫力系数分布的影响，相比热流的影响要弱得多。化学反应使得气体压缩和气体膨胀更剧烈，在前体脱体激波层化学反应致气体压缩性更强，波后压力更大，因此反应气体的头部激波更靠近物体，头部区域的压力要高于TR气体，但在身部膨胀区，热化学非平衡效应加剧了膨胀，使压力减小，以致TR气体计算的压力要稍高些，见图10。对于摩檫力系数来说，无论头部还是身部都是TR气体计算值高于反应气体，见图11，主要是热化学反应真实气体分子能量因振动能激发与离解吸热而致能量降低，跨越脱体激波层气流速度较仅考虑转动能激发的TR气体波后速度更小，以致物面切向速度变化梯度低于TR气体所致，这种情况在φ＝0°的迎风子午面因高超声速再入脱体激波明晰强烈表现更为明显，而在φ＝180°背风子午面因脱体激波较弱使得考虑与不考虑热化学反应真实气体效应，两种情况计算值差别不大，图11中摩擦力系数在φ＝0°、180°两个子午面的变化曲线显示出热化学非平衡效应对返回器表面摩檫力系数造成影响这一变化规律。因此，头部压力增大对俯仰力矩的贡献与身部摩擦力减小的贡献相抵消，造成高温气体热化学非平衡效应对这种返回器配平攻角的影响较小。为了定量化分析上述两种气体模型计算得到的俯仰力矩系数变化特点，图12蓝色虚点线与蓝色实线绘出两种气体模型计算的该返回器以攻角－20°再入120～80 km高度所受的俯仰力矩系数比较，看出两者相差微弱，表明高温热化学非平衡效应对返回器俯仰力矩系数影响甚微。

图12、图13绘出了返回器以来流速度7.5 km/s攻角－20°再入120～80 km高度的气动力系数随高度变化规律。随着飞行高度的增加，阻力系数是不断增大的，升力系数和升阻比则迅速下降，压心前移，引起俯仰力矩系数(负值为低头力矩)在数值上不断增大。如果要达到配平状态，则需要更大的负向攻角产生正的抬头力矩才能实现，也就是说随着飞行高度增加，配平攻角是增大的。在高空稀薄流域，压力对气动力系数的贡献随高度的变化比较小，但摩擦力的贡献则是随高度的增加而增大，这也是引起配平攻角随飞行高度有较大变化的主要原因。

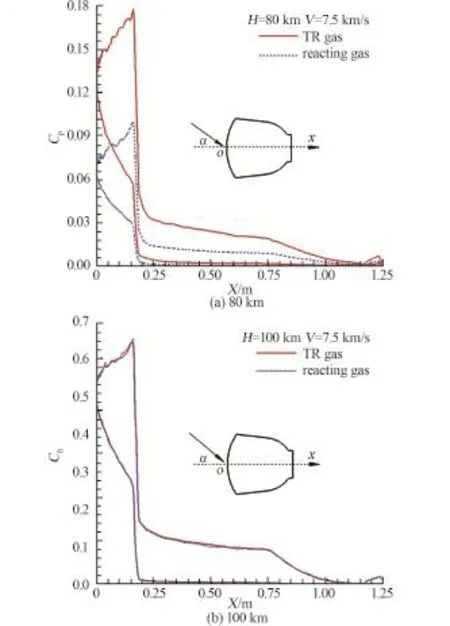
图9 化学反应对返回器0°和180°子午面热流影响比较Fig.9 Effect of chemical reactions on surface heat flux around reentry capsule along φ ＝0°，180°

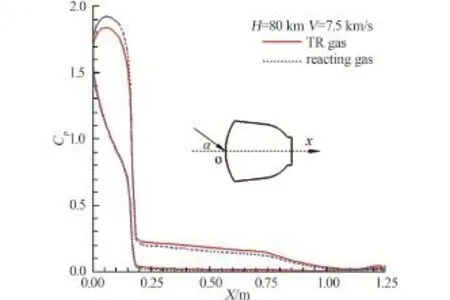
图10 化学反应对返回器0°和180°子午面压力影响比较Fig.10 Effect of chemical reactions on surface pressure around reentry capsule along φ＝0°，180°

图11 化学反应对返回器0°和180°子午面摩檫力影响比较Fig.11 Effect of chemical reactions on surface friction around reentry capsule along φ＝0°，180°

图12 俯仰力矩和压心系数随高度变化Fig.12 Pitching moment and center of pressure coefficient vs flight altitude

图13 升阻特性随高度变化Fig.13 Lift-drag feature vs flight altitude

4 结论

本文给出了双原子分子转动和振动松弛碰撞数计算公式、TCE化学反应模型，建立了模拟分子非弹性碰撞先后次序的算法，采用基于流场直角与物面非结构混合网格的DSMC方法模拟了钝体返回器不同再入速度、不同飞行高度下的热化学非平衡流动现象和气动力/热变化特性，得出以下几点结论:

1)在近连续滑移区，流场大部分区域都处于平衡态，只有在较窄的激波层区域，平动温度、转动温度和振动温度之间存在着较严重的非平衡；随着稀薄度的不断增大，激波层和边界层逐渐融合，热力学非平衡区域扩大至整个压缩区和尾迹区；

2)在返回器再入80 km高度，气体分子发生剧烈的化学反应，流场呈现化学非平衡状态。随高度增加，化学反应逐渐减弱，但探月返回器若以近第二宇宙速度从月球再入返回，在离地面100 km高空的稀薄条件下也会产生强烈的离解反应。

3)高温真实气体效应对低高度的表面热环境影响较大，但对表面压力和摩擦力分布影响相对较小，随着飞行高度增加，影响呈不断减弱的趋势。

4)稀薄气体效应对探月返回器的气动特性影响显著，使升阻比降低，压心前移，配平攻角增大。

（

）

[1]Boyd I D.Modeling of associative ionization reactions in hypersonic rarefied flows[J].Physics of Fluids，2007，19(9): 3-14.

[2]Ozawa T，Levin D A，Nompelis I，et al.Particle and continuum method comparison of a high-altitude，extreme-Machnumber reentry flow[J].Journal of Thermophysics and Heat Transfer，2010，24(2):225-240.

[3]Lofthouse A J，Scalabriny L C，Boyd I D.Hypersonic aerothermodynamics analysis across nonequilibrium regimes using continuum and particle methods[R].AIAA 2007-3903，2007.

[4]Wen C Y，Massimi H S，Chen Y S，et al.Numerical simulations of nonequilibrium flows over rounded models at reentry speeds[R].AIAA 2012-5906，2012.

[5]Bird G A.Molecular gas dynamics and the direct simulation of gas flows[M].Oxford:Clarendon Press，1994:123-256.

[6]梁杰，阎超，杜波强.基于两级直角网格结构的三维DSMC算法研究[J].空气动力学学报，2010，28(4):466-471.Liang Jie，Yan Chao，Du Boqiang.An algorithm study of three-dimensional DSMC simulation based on two-level Cartesian coordinates grid structure[J].Acta Aerodynamica Sinica，2010，28(4):466-471.(in Chinese)

[7]梁杰，阎超，杨彦广，等.过渡区侧向喷流干扰的并行DSMC数值模拟研究[J].宇航学报，2011，32(5):1012-1018.Liang Jie，Yan Chao，Yang Yanguang，et al.Parallel DSMC simulation of lateral jet interaction in rarefied transitional region[J].Journal of Astronautics，2011，32(5):1012-1018.(in Chinese)

[8]沈青.稀薄气体动力学[M].北京:国防工业出版社，2003:246-247.Shen Qing.Rarefied Gas Dynamics[M].Beijing:National Defense Industry Press，2003:246-247.(in Chinese)

[9]Lumpkin F E，Hass B L，Boyd I D.Resolution of differences between collision number definition in particle and continuum simulations[J].Physics of Fluids A:Fluid Dynamics(1989-1993)，1991，3(9):2282-2284.

[10]Boyd I D.Rotational and vibrational nonequilibrium effects in rarefied hypersonic flow[J].Journal of Thermophysics and Heat Transfer，1990，4(4):478-484.

[11]Parker J G.Rotational and vibrational relaxation in diatomic gases[J].Physics of Fluids，1959，2(4):449-462.

[12]Millikan R C，White D R.Systematics of vibrational relaxation[J].The Journal of Chemical Physics，1963，39(12): 3209-3213.

[13]Park C.Problems of rate chemistry in the flight regimes of aeroassisted orbital transfer vehicles[C]//Progress in Astronautics and Aeronautics，AIAA，New York，1985，96:511-537.

[14]Gimelshein N E，Gimelshein S F，Levin D A，et al.Reconsideration of DSMC models for internal energy transfer and chemical reactions[C]//23rd International Symposium of Rarefied Gas Dynamics，American Institute of Physics，2003: 349-357.

Numerical Simulation of Rarefied Gas Thermochemical Nonequilibrium when Lunar Exploration Vehicle Re-entering into Atmosphere

LIANG Jie，LI Zhihui∗，DU Boqiang，FANG Ming
(Hypervelocity Aerodynamics Institute，China Aerodynamics Research and Development Center，Mianyang 621000，China)

The Direct Simulation Monte Carlo(DSMC)method was developed to simulate rarefied gas flows around complex bodies with internal energy excitation and thermochemical nonequilibrium effect of five air species，using a hybrid grid technique of Cartesian coordinate meshes and surface unstructured triangular cells.The nonequilibrium flowfield characteristics and their effects on surface parameters distribution around blunt re-entry capsule in rarefied flow regime were numerically simulated under the re-entering velocities of 7.5km/s and 10.6km/s，respectively.The computational results showed that intensive thermochemical nonequilibrium occurred in the rarefied transitional region under lunar return velocity.In near continuum slip flow regime，the great degrees of translational，rotational and vibrational nonequilibrium only exited in the shock wave layer.While thermodynamic nonequilibrium distributed in the whole compress and wake regions at high rarefied flow regime.The high temperature real gas effect affected the surface thermal environment significantly and impacted relatively weak on the surface pressure and friction.It is indicated that the effect of thermochemical nonequilibrium must be considered up to 100km during the re-entering into the atmosphere of the lunar exploration vehicle.

lunar exploration reentry vehicle；rarefied flow region；thermochemical nonequilibrium；DSMC method；numerical simulation

V211.3

A

1674-5825(2015)03-0295-08

2014-09-11；

2015-03-15

国家自然科学基金(91016027、11325212)；973计划(2014CB744100)；国防基础科研基金(51313030104)

梁杰(1966－)，男，博士，研究员，研究方向为稀薄气体动力学的数值方法及应用。E-mail:liangjie29501＠163.com

李志辉(1968－)，男，博士，研究员，研究方向为跨流域空气动力学。E-mail:zhli0097＠x263.net