空间机械臂刚柔耦合动力学模拟及小波基模糊神经网络控制

梁 捷,陈 力,梁 频,2

(1.福州大学机械工程及自动化学院，福州350108；2.中国空气动力研究与发展中心，绵阳621000；3.电子科技大学航空航天学院，成都611731)

·基础研究·

空间机械臂刚柔耦合动力学模拟及小波基模糊神经网络控制

梁 捷1,2,3,陈 力1,梁 频1,2

(1.福州大学机械工程及自动化学院，福州350108；2.中国空气动力研究与发展中心，绵阳621000；3.电子科技大学航空航天学院，成都611731)

研究了关节和杆件双重柔性影响下空间机械臂系统的动力学模拟，运动控制算法设计和臂杆、关节双重柔性振动的主动抑制问题。利用线动量、角动量守恒关系，并基于拉格朗日方程、线性扭转弹簧及假设模态法建立系统动力学模型。为解决传统奇异摄动法应用受关节柔性限制问题，引入了一种关节柔性补偿控制器，以适当提高系统关节的等效刚度；并基于奇异摄动理论，将系统分解成独立时间尺度的柔性臂子系统和电机力矩动力子系统，借助小波基模糊神经网络的优良特性，将轨迹跟踪的角度误差及角速度误差输入到网络中，通过一阶梯度寻优算法来优化整个网络，降低柔性振动的影响，以达到高精度控制的要求的。计算机数值仿真对比试验证实了该方法的可靠性和有效性。

漂浮基空间机械臂系统；柔性关节；柔性臂；动力学模拟；关节柔性补偿器；小波基模糊神经网络；一阶梯度寻优算法

1 引言

作为航天活动的重要工具，空间机械臂被期望执行远比现在更复杂的任务，如协助或替代航天员完成大量危险艰巨的太空作业、太空实验以及空间站的在轨燃料加注、装配、维护等[1，2]。因此，空间机械臂系统的研究受到美国、欧洲及日本等发达国家航天机构的极大重视，相关理论及技术已成为当前航天高技术领域一个研究热点[3-16]。伴随着我国载人航天计划的顺利进行，我国近年来对空间机械臂技术也投入了大量的研发经费，并将其定位为载人航天任务中需要开展、解决的关键技术问题[2]。出于国家安全及防卫的考虑，我国掌握并具有空间机械臂自主在轨服务技术是必然的，其相关理论研究成果有重要意义。

由于空间机械臂的空间站载体处于太空失重状态，系统满足动量守恒、动量矩守恒或两者均守恒的动力学约束；并由于技术和发射费用等原因，其臂杆及关节的柔性及振动对机械臂的动态特性(如定位精度、平稳性等)影响较大，甚至影响系统安全性[17]。因此考虑关节和杆件双重柔性影响下的漂浮基空间机械臂的智能控制问题变得非常复杂，提出了许多有挑战意义的新问题。带有柔性关节的空间机械臂[15]最大控制难点是其机械臂各关节铰的电机输出转角与该关节铰实际转角存在不同步性，这相当于在关节驱动器和被动连杆间设置了一个力矩滤波器，关节刚度越小，滤波器的带宽也越窄。而空间机械臂的臂杆柔性[10，12，13，16]主要影响机械臂运动的精确控制，可将视为一个强耦合、强非线性的系统。为此，本文在控制策略上，将系统视为由表征系统刚性运动和臂杆振动的柔性臂子系统和表征关节柔性的电机力矩动力子系统构成。引入一种关节柔性补偿器，以提高关节的等效刚度。并借助于小波基模糊神经网络的优良特性，将轨迹跟踪的角度误差及角速度误差输入到网络中，通过一阶梯度寻优算法来优化整个网络，从而解决柔性振动的影响，以达到高精度控制的要求。

2 系统动力学模拟

不失一般性，仅考虑作平面运动的综合关节和杆件的空间机械臂系统，结构如图1所示。

图1 空间机械臂系统Fig.1 The space manipulator system

该系统由空间站载体B0，刚性臂B1和柔性臂B2及和两个弹性关节Oi(i＝1，2)组成。

各符号定义如下:l0为关节O0到O1的距离；li(i＝1，2)为Bi的长度；a1为关节O1到杆B1质心OC1的距离；mi(i＝1，2)为Bi的质量；Ii为Bi相对质心OCi(i＝0，1)的转动惯量；M为系统的总质量；C为系统的整体质心；O－XY为系统的惯性坐标系。Oi－xiyi为Bi(i＝0，1，2)连体坐标系，ei为沿xi(i＝0，1，2)上的单位矢量。ri为质心Bi(i＝0，1)相对惯性坐标系的位置矢量rc为系统总质心位置矢量；θ0为载体姿态角；θi为关节Oi(i＝1，2)处轴xi－1与xi的夹角；θmi为第i(i＝1，2)个电机转角。EI为柔性杆的抗弯刚度；ρ为柔性杆单位长度的平均密度。

柔性关节采用Spong假设，将其等效为线性扭转弹簧模型，忽略电机转子的质量，只考虑电机转子的转动动能。设柔性杆满足Euler-Bernoulli小变形假设，弹性变形为其中 φi(x2)为模态函数向量，ηi(t)为模态坐标向量，n为模态截断项数。由于低阶模态对柔性杆弹性振动起主导作用，故取前2阶模态。柔性杆B2为悬臂梁，其模态函数选为式(1):

根据系统几何位置关系，载体、刚性臂的质心及柔性臂任一点的位置矢量如式(2):

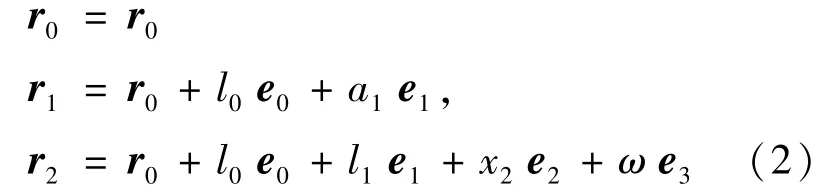
忽略微弱的重力并假设系统不受外力作用，整个系统的线动量、角动量守恒。而线动量是完整约束，对线动量方程积分便是总质心定律。不失一般性设系统初始动量为零，则线动量、角动量守恒方程可分别描述为式(3)、(4):

由式(2)和式(3)可得式(5):

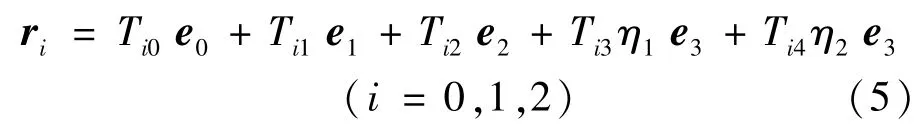
式中，Tij仅与系统惯性参数有关。将式(5)及其时间导数代入式(4)中角动量守恒定关系式，并整理得式(6)；

其中，Fi(i＝1，…，7)是系统惯性参数和广义坐标(θ1，θ2，η1，η2)的函数。

分析可知系统总动能由载体动能、刚性杆动能、柔性杆动能及电机转子动能组成，如式(7):

而系统的总势能由柔性臂的弯曲应变能和柔性铰的弹性势能组成，如式(8):

由拉格朗日第二类方程及系统动能和势能表达式，可推导出考虑关节和臂杆双重柔性影响下的空间机械臂系统动力学方程如式(9)～(11):

考虑到节省控制燃料的实际需求，研究载体位置和姿态均不受控制的空间机械臂系统控制很有必要。对式(9)进行矩阵分解展开得式(12)、(13):

式中，下标r与广义坐标θ0对应，f与广义坐标θf、η对应。由式(12)解出并代入式(13)可得，综合考虑关节和臂杆双重柔性影响下载体位置和姿态均不控的空间机械臂动力学方程为式(14)～(16):

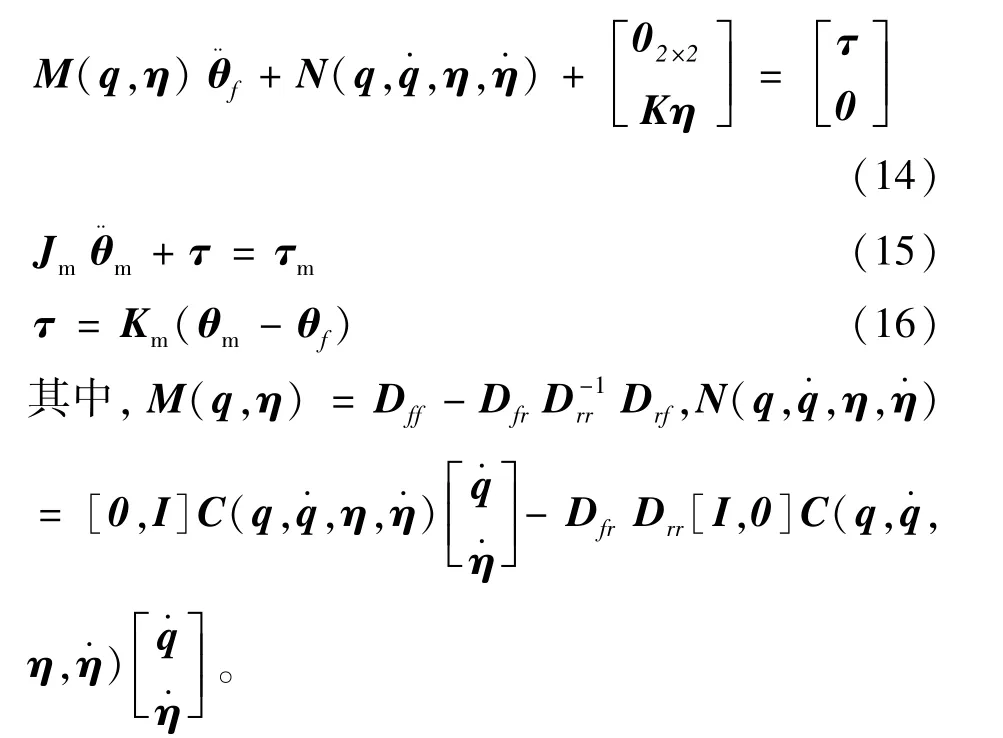
式(14)反映系统的刚性运动和柔性杆振动，与一般柔性臂系统具有相似的动力学模型；式(15)表征因关节柔性而引起的电机力矩动态特性。文中控制目标为，针对系统动力学方程(14)、(15)和(16)，设计控制律τm，使空间机械臂的两关节铰运动轨迹θf稳定地跟踪给定的期望轨迹θd。

3 基于柔性关节补偿的小波基模糊神经网络控制

空间机械臂与空间站载体之间存在着强烈的动力学耦合作用，又兼具臂杆柔性和关节柔性，这两种柔性特征，给控制器的设计带来了极大的挑战。对带有柔性关节的空间机械臂最大控制难点是其机械臂各关节铰的电机输出转角与该关节铰实际转角存在不同步性，这相当于在关节驱动器和被动连杆间设置了一个力矩滤波器，关节刚度越小，滤波器的带宽也越窄。而空间机械臂的臂杆柔性主要影响是机械臂运动的精确控制，可将视为一个强耦合、强非线性的系统。为此，本文在控制策略上，将系统视为由表征系统刚性运动和臂杆振动的柔性臂子系统和表征关节柔性的电机力矩动力子系统构成。对电机力矩动力子系统，引入一种关节柔性补偿器，以提高关节的等效刚度。对柔性臂子系统，借助于模糊小波神经网络的优良特性，将轨迹跟踪的角度误差及角速度误差输入到网络中，通过一阶梯度寻优算法来优化整个网络，以解决柔性振动的影响，提高精度控制。

为引入关节柔性补偿器，将式(15)和(16)整理得电机力矩动态方程如式(17):

可见关节柔性扭转刚度矩阵K－1m起到了类似力矩滤波器的作用，该值越小系统的控制带宽会越宽。

初步选取系统的控制输入规律如如式(18)、关节柔性补偿器如式(19):

其中，τn为新定义的控制量，τf为关节柔性补偿器，Kf∈ RR2×2为对角、正定的柔性补偿系数矩阵，且Kn＝I＋Kf。将式(18)和式(19)代入式(17)得式(20):

比较式(20)和式(17)可知，通过适当的选取Kf可以将关节的等效刚度调整到期望的数值，以提高力矩滤波器的带宽。

根据奇异摄动理论可将新定义的控制量τn可如式(21)分解:

其中，τJ和τL分别对应柔性臂子系统和电机力矩动力子系统的控制律。定义一个非常小的数ε1，使KnKm＝K2/ε21，K2为对角正定参数矩阵。则方程(20)进一步整理为式(22):

为使电机力矩动力子系统(22)的稳定，设定一力矩微分反馈控制器如式(23):

式中，KL为对角正定参数矩阵。在快变时间尺度下，式(22)的右边可视为常数，因此通过恰当的选取KL可保证子系统(22)稳定。

若设ε1＝0，则代入式(14)可得柔性臂子系统如式(24):

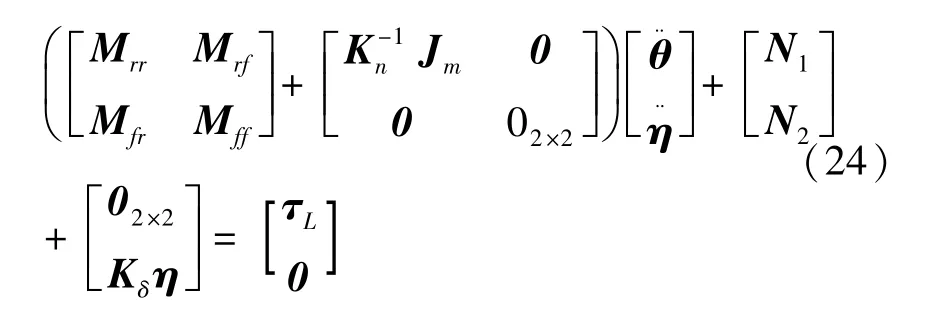
式中，下标r与广义坐标θf对应，下标f与广义坐标η对应。因此，表征系统刚性运动的动力学方程如式(25):

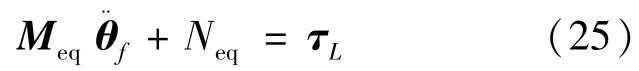
分析式(25)可知，臂杆柔性与机械臂刚性运动存在动力学耦合作用，相当于系统内在干扰。因此通过提高控制律τL的鲁棒性，可以克服柔性振动的影响，达到高精度运动控制的要求。为此，本小节针对柔性臂子系统设计小波基模糊神经网络的控制方案，以使机械臂关节铰能有效地跟踪指定的期望轨迹。系统的控制框图如图2所示。

图2 空间机械臂控制框图Fig.2 Schematic diagram of the space manipulator system

图2中θ1d和θ2d是机械臂关节铰的期望运动轨迹；和是相应的期望运动速度。跟踪误差的论域经输入量化因子 Kc1、Kc2的作用，转化为小波基模糊神经网络(FWNN)的输入论域；y1和y2是FWNN网络的输出；为输出因子kui组成的矩阵，该因子将FWNN网络的输出论域转化为实际输出论域得到机械臂关节铰的控制力矩如式(26):

式中，矩阵KW值之间相对大小亦反映了机械臂关节铰间的控制耦合作用。

4 小波基模糊神经网络

图2的控制框图中的小波模糊神经网络，是采用小波基函数作为模糊隶属度函数，并利用神经网络去实现模糊化、模糊推理和去模糊化的过程。这里介绍该网络结构和在线学习算法。

4.1 小波基模糊神经网络的结构

FWNN的结构图如图3所示[18]，共有4层。第一层:为输入层，该层的各个结点与输入值连接，并传递到第二层。

图3 小波基模糊神经网络Fig.3 Wavelet based fuzzy neural network

第二层:每个结点表示一个模糊语言词集值，计算各输入分量的语言词集的隶属度函数μAij(xi)。隶属度函数采用为小波基函数，其母小波函数如式(27):

各语言词集上定义的隶属度函数就是通过平移和伸缩母小波函数来得到。即，对于第i个输入第j个词集Aij，其小波隶属度函数可定义为式(28):

式中，cij和ωij分别为伸缩和平移系数。为简化网络结构，每个输入xi，在本文仅定义三个模糊语言词集{P，Z，N}＝{正，零，}。

第三层:该层用于计算条规则的适用度，一个节点代表一条模糊规则。这里采用式(29)所示乘法计算本层输出

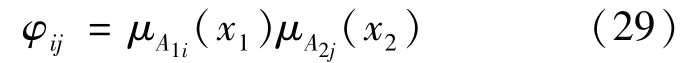
第四层:实现的是去模糊化过程，根据式(30)计算FWNN的输出。

式中，Wij为网络权值，表示各模糊规则输出对应的语言词集的中心值。

4.2 在线学习算法

对于载体位置、姿态均不控的柔性臂子系统共需2个关节伺服控制器。为此，采用两个FWNN子网。子网1的网络权值、伸缩系数及平移系数分别标记为W1，ω1，c1；子网2的网络权值、伸缩系数及平移系数分别标记为W2，ω2，c2。由上节知的柔性臂子系统的控制力矩τL为跟踪误差ei、误差率、输出因子矩阵KW、子网1与 2的网络权值、伸缩系数及平移系数的函数。为此，首先利用反向传播算法(BP算法)对一阶梯度进行求解，再通过一阶梯度寻优算法在线学习参数在线学习的目标函数可定义为式(31):

其中，ei为第i个关节角的轨迹跟踪误差。学习算法如式(32)～(35):

其中，下标k＝1，2；i＝1，2；j＝1，2，3；η1、η2、η3和η4为参数学习率。

5 仿真案例研究

以图1所示考虑关节和臂杆双重柔性影响下的空间机械臂为例，设系统真实参数如下:载体的参数m0＝40 kg，l0＝1．5 m，J0＝35 kg·m2；刚性杆的参数:m1＝4 kg，l1＝2 m，a1＝1 m，J1＝2 kg·m；柔性杆的参数:l2＝2 m，ρ＝1 kg/m，EI＝200 N·m2，J1m＝J2m＝0.08 kg·m2，K1m＝K2m＝15 N·m/rad。

机械臂各关节的期望轨迹为(单位:rad)

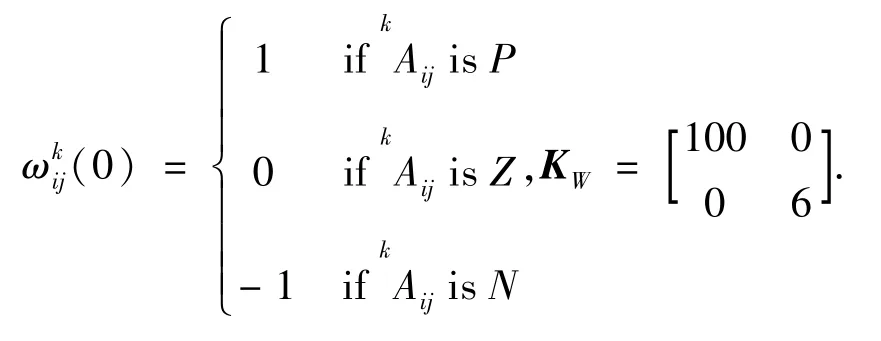
仿真时间8 s，仿真结果如图4～13所示。

图4 关节角θ1和θ2的轨迹跟踪图Fig.4 Trajectories tracking of θ1and θ2

图5 轨迹跟踪误差图Fig.5 Trajectory tracking error

图6 柔性模态坐标变量η1的变化曲线图Fig.6 Curve of the modal coordinate variable η1

本文进行了三组仿真试验。第一组直接采用文中设计的联合控制方案式(21)对系统进行数值仿真试验。仿真结果如图4～9所示。由图4和图5可以看出，该控制方案能使空间机械臂的关节铰θ1和θ2有效地跟踪期望轨迹；由图6～9可以看出，文中设计的基于柔性关节补偿器的小波基模糊神经网络控制方案能够克服机械臂各关节铰的电机输出转角与该关节铰实际转角存在不同步性所带来问题，有效地抑制了弹性关节的柔性振动；同时柔性臂B2的柔性振动也得到抑制，这是由于FWNN强大的鲁棒性克服了臂杆柔性振动对空间机械臂刚性运动的干扰，所设计的控制方案的优点在于:不需要反馈、测量柔性振动模态，大大简化了控制器结构，便于工程实际应用。

图7 柔性模态坐标变量η2的变化曲线图Fig.7 Curve of the modal coordinate variable η2

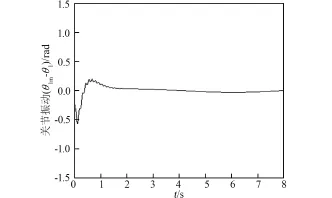
图8 关节O1的柔性振动图Fig.8 The flexible vibration of joint O1

图9 关节O2的柔性振动图Fig.9 The flexible vibration of joint O2

图10 关节角θ1和θ2的轨迹跟踪图（降低关节等效刚度）Fig.10 Trajectories tracking of θ1and θ2（Reduce the joint equivalent stiffness）

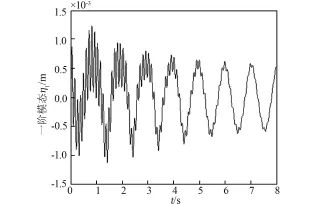
图11 柔性模态坐标变量η1的变化曲线图（降低关节等效刚度）Fig.11 Curve of the modal coordinate variable η1（Reduce the joint equivalent stiffness）

图12 柔性模态坐标变量η2的变化曲线图（降低关节等效刚度）Fig.12 Curve of the modal coordinate variable η2（Reduce the joint equivalent stiffness）

第二组为考虑空间机械臂关节柔性和臂杆柔性相互之间的影响而进行的仿真试验。仿真结果如图10～14所示。将文中关节柔性补偿器式(19)中的控制参数Kf的取值由6改为2(即Kf＝2，这相当于降低了关节等效刚度，Kf＝0相当于关闭关节柔性补偿器)。

由图10可以看出，空间机械臂系统的运动控制精度变差；图11～14可以看出，柔性臂B2、关节O1和关节O2均出现了大幅度震荡，原因是此时关节柔性补偿力度不够(Kf＝2)，导致关节柔性振动增强进而激发了臂杆柔性振动，而臂杆柔性振动又与刚性运动存在耦合干扰作用，因此最终致使整个控制系统失效。

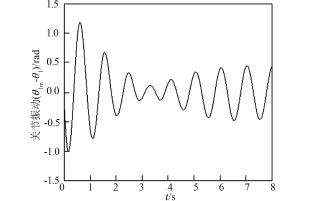
图13 关节O1的柔性振动图（降低关节等效刚度）Fig.13 The flexible vibration of joint O1（Reduce the joint equivalent stiffness）

图14 关节O2的柔性振动图（降低关节等效刚度）Fig.14 The flexible vibration of joint O2（Reduce the joint equivalent stiffness）

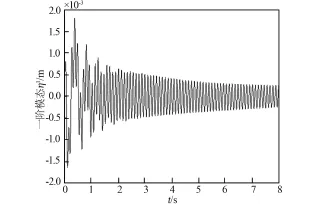
图15 柔性模态坐标变量η1的变化曲线图（基于PID的控制方案）Fig.15 Curve of the modal coordinate variable η1（based on control scheme of PID）

图16 柔性模态坐标变量η2的变化曲线图（基于PID的控制方案）Fig.16 Curve of the modal coordinate variable η2（based on control scheme of PID）

第三组为采用第一组仿真中相同的相同柔性补偿参数，而柔性臂子系统的控制力矩τL采用惯常的PID控制所进行的仿真实验。仿真结果如图15～16所示。从仿真图6～7和图15～16对比可以看出，文中提出的柔性关节补偿器的小波基模糊神经网络控制方案能够有效抑制柔性臂B2的柔性振动，而在基于相同柔性关节补偿器的PID控制方案不能主动抑制柔性臂B2的振动，这也是柔性关节补偿器的小波基模糊神经网络控制方案与惯常PID控制方案的比较优势之所在。

6 结论

1)文中对考虑关节和臂杆双重柔性影响下的空间机械臂刚柔耦合系统进行了动力学模拟。由于在系统动力学模型的推导过程中结合系统动量守恒关系消去了载体位置项，这使得文中设计的联合控制方案具有不需要测量反馈载体位置、速度和加速度的显著优点。

2)利用关节柔性补偿器，解除了传统奇异摄动法受关节柔性的约束，导出了空间机器人经关节柔性补偿后的电机力矩动力子系统和柔性臂子系统。

3)针对电机力矩动力子系统，引入一种关节柔性补偿器，以提高关节的等效刚度，同时设计了力矩微分反馈控制器来保证子系统的稳定；针对柔性臂子系统式，借助于小波基模糊神经网络的优良的鲁棒性克服了臂杆柔性振动对空间机械臂刚性运动的干扰，所设计的控制方案的优点在于:不需要反馈、测量柔性振动模态，大大简化了控制器结构，提高了控制精度，便于工程实际应用。

4)通过三组仿真对比试验可以看出，文中所设计的基于关节柔性补偿器的小波基模糊神经网络控制方案能够弥补系统惯性参数不确定及柔性关节引起的转动误差，保证空间机械臂完成期望运动轨迹的渐近跟踪；并能够有效抑制柔性关节和柔性臂引起的系统柔性振动，保证系统控制精度和稳定性。

（

）

[1]周建平.我国空间站工程总体构想[J].载人航天，2013，19(2):1-10.Zhou Jianping.Chinese space station project overall vision [J].Manned Spaceflight，2013，19(2):1-10.(in Chinese)

[2]于登云，孙京，马兴瑞.空间机械臂技术及发展建议[J].航天器工程，2007，16(4):1-8.Yu Dengyun，Sun Jing，Ma Xingrui.Suggestion on development of chinese space manipulator technology[J].Spacecraft Engineering，2007，16(4):1-8.(in Chinese)

[3]Pisculli A，Felicetti L，Gasbarri P，et al.A reaction-null/Jacobian transpose control strategy with gravity gradient compensation for on-orbit space manipulators[J].Aerospace Science and Technology，2014，38:30-40.

[4]Jarzębowska E，Pietrak K.Constrained mechanical systems modeling and control:A free-floating space manipulator case as a multi-constrained system[J].Robotics and Autonomous Systems，2014，62(10):1353-1360.

[5]Abiko S，Hirzinger G.An adaptive control for free-floating space robot by using inverted chain approach[C]//Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems，San Diego，CA，USA:IEEE，2007:2236-2241.

[6]Walker M W，Wee L B.Adaptive control of space-based robot manipulators[J].IEEE Transactions on Robotics and Automation，1992，7(6):828-835.

[7]李俊峰，王照林.带空间机械臂的充液航天器姿态动力学研究[J].宇航学报，1999，20(2):81-86.Li Junfeng，Wang Zhaolin.Study on attitude dynamics of a liquid-filled spacecraft with manipulators[J].Journal of Astronautics，1999，20(2):81-86.(in Chinese)

[8]丁希仑，俞玉树.一种多旋翼多功能空中机器人及其腿式壁面行走运动规划[J].航空学报，2010，31(10):2075-2086.Ding Xilun，Yu Yushu.A multi-propeller and multi-function aero-robot and its motion planning of leg-wall-climbing[J].Acta Aeronouticaet Astronautica Sinica，2010.31(10): 2075-2086.(in Chinese)

[9]阎绍泽，黄铁球，吴德隆.空间飞行器柔性附件动力学建模方法研究[J].导弹与航天运载技术，1999(2):31-39.Yan Shaoze，Huang Tieqiu，Wu Delong.Study on dynamics modeling of a flexible appendage of spacecraft[J].Missiles and Space Vehicles，1999(2):31-39.(in Chinese)

[10]李青，王天舒.高频激励下旋转柔性臂逆动力学模态自适应方法研究[J].空间科学学报，2008，28(4):345-349.Li Qing，Wang Tianshu.Adaptive mode method in inverse dynamics of a rotating flexible manipulator with high-frequency excitation[J].Chinese Journal of Space Science，2008，28 (4):345-349.(in Chinese)

[11]张大伟，梁常春，危清清.机械臂辅助舱段转位轨迹跟踪控制与精度分析[J].载人航天，2014，20(2):103-109.Zhang Dawei，Liang Changchun，Wei Qingqing.Trajectory tracking control and accuracy analysis of space robotic arm assisted cabin redocking[J].Manned Spaceflight，2014，20 (2):103-109.(in Chinese)

[12]吴立成，孙富春，孙增圻，等.柔性空间机器人振动抑制轨迹规划算法[J].机器人，2003，25(3):250-254.Wu Licheng，Sun Fuchun，Sun Zengqi，et al.Optimal trajectory planning of flexible space robot for vibration reducing [J].Robot，2003，25(3):250-254.(in Chinese)

[13]洪在地，贠超，陈力.柔性臂漂浮基空间机器人建模与轨迹跟踪控制[J].机器人，2007，29(1):92-96.Hong Zaidi，Yun Chao，Chen Li.Modeling and trajectory tracking control of a free-floating space robot with flexible manipulators[J].Robot，2007.1，29(1):92-96.(in Chinese)

[14]梁捷，陈力.具有时延的漂浮基空间机器人基于泰勒级数预测、逼近的改进非线性反馈控制[J].航空学报，2012，33(1):163-169.Liang Jie，Chen Li.Improved Nonlinear feedback control for free-floating space-based robot with time-delay based on predictive and approximation of taylor series[J].Acta Aeronouticaet Astronautica Sinica，2012，33(1):163-169.(in Chinese)

[15]梁捷，陈力.关节柔性的漂浮基空间机器人基于奇异摄动法的轨迹跟踪非奇异模糊Terminal滑模控制及柔性振动抑制[J].振动与冲击，2013，32(23):6-12.Liang Jie，Chen Li.Nonsingular fuzzy terminal sliding mode control elastic vibration suppressing of a free-floating space robot with flexible joints based on trajectory tracking of the singular perturbation method[J].Journal of Vibration and Shock，2013，32(23):6-12.(in Chinese)

[16]梁捷，陈力.基于虚拟力概念的柔性臂空间机器人模糊退步自适应控制算法设计[J].计算力学学报，2014，31 (4):467-473.Liang Jie，Chen Li.Fuzzy Adaptive algorithm using backstepping controller for flexible arm space robot based on virtual control force conception[J].Chinese Journal of Computational Mechanics，2014，31(4):467-473.(in Chinese)

[17]李大明，饶炜，胡成威，等.空间站机械臂关键技术研究[J].载人航天，2014，20(3):238-242.Li Daming，Rao Wei，Hu Chengwei，et al.Key technology review of the research on the space station manipulator[J].Manned Spaceflight，2014，20(3):238-242.(in Chinese)

[18]彭金柱，王耀南，孙炜.基于混合学习算法的模糊小波神经网络控制[J].湖南大学学报(自然科学版)，2006，33 (2):51-54.Peng Jinzhu，Wang Yaonan，Sun Wei.Fuzzy wavelet neural networks control based on hybrid learning algorithm[J].Journal of Hunan University(Natural Sciences)，2006，33(2): 51-54.(in Chinese)

The Rigid-Flexible Coupling Dynamics Simulation and Wavelet Based Fuzzy Neural Network Control for Space Manipulator

LIANG Jie1，2，3，CHEN Li1，LIANG Pin2
(1.Department of Mechanical Engineering and Automation，Fuzhou University，Fuzhou 350108，China；2.China Aerodynamics Research and Development Center，Mianyang 621000，China；3.School of Astronautics＆Aeronautic，University of Electronic Science and Technology of China，Chendu 611731，China)

The dynamics simulation of flexible joints and flexible arm space robot system，motion control algorithm design and hierarchical points order active inhibition problem of arm and joints double flexible vibration that all under the situation of parameter uncertain were discussed in this paper.With the conservation relationship of linear and angular momentum，a system dynamics model was established by Lagrange equations，linear torsion spring and hypothesis modal method.To solve the problem that the application of traditional singular perturbation approach was limited by joint flexibility，a joint flexibility compensation controller was introduced，which could properly enhance the equivalent stiffness of joints.Then，based on singular perturbation theory，the whole system was resolved into flexible arm subsystem and motor moment power subsystem on the basis of joint flexible compensation controller and singular perturbation technology.Taking advantage of the excellent characters of the wavelet fuzzy neural network，the authors input the trajectory tracking angle error and angular velocity error to the network，to optimize the whole network by a gradient optimization algorithm，so as to solve the influence of flexiblevibration，thus achieve high precision control requirements.Computer numerical simulation comparison experiment testified the reliability and availability of this scheme.

free-floating space manipulator system；flexible-joint；flexible-arm；dynamics simulation；joint flexible compensation controller；fuzzy wavelet neural network；a gradient optimization algorithm

TP241

A

1674-5825(2015)03-0286-09

2015-01-14；

2015-04-17

国家自然科学基金(11372073，11072061)

梁捷(1971－)，男，博士，博士后，研究方向为空间机械臂动力学与控制。E-mail:myamoy81＠sina.com