工科矩阵分析课程教学实践与探讨
2015-12-07路利军曹丽娜
路利军+曹丽娜
摘要:矩阵分析是数学的一个重要分支,理论严谨、方法独特,可以培养学生的抽象思维能力、逻辑论证能力和理论的实际应用能力。本文考虑到专业发展的需要,调整了教学模式、教学手段和课堂教学方式,以期能激发学生学习热情,提高当前教学效果,实现教学相长。
关键词:矩阵分析;教学模式;教学手段;课堂教学形式
中图分类号:G642.41 文献标志码:A 文章编号:1674-9324(2015)23-0146-02
一、引言
目前,作为大学数学重要分支的“矩阵分析”,其理论和方法表达简洁、刻画透彻,是工科必须掌握的数学理论之一。所以,许多高校都将其设置为高年级本科生或研究生的公共基础课程。然而,“矩阵分析”本身是一门发展完善、理论严谨、方法独特的基础课,目前工科矩阵分析理论性太强,过分强调抽象思维能力,而忽略工程应用介绍,使学生难以理解,在教学中很难激发学生兴趣。矩阵公式推演和逻辑证明——抽象的符号表达并进行相应的“运算”,让学生感到这一切像是在玩数字游戏,很多时候甚至无法理解所遵循的游戏规则。任课教师也常常感到学生数学功底不够厚实,不会灵活地利用所学过的知识理解遇到的问题,联系实际解决问题的能力更是薄弱。这些问题的突出存在,不仅影响了后续课程的学习,也不利于高素质创新型人才的培养。因此,考虑到专业发展的需要,笔者调整了教学模式、教学手段和教学方式并且注重工程应用,激发学生对于矩阵分析课程的兴趣,希望能提高当前的教学质量,实现教学相长。
二、积极调整教学模式
在现代教学中,比较有代表性的教学模式是“传授—接受”模式。教师讲解定量、推导公式,学生被动地听讲,无暇顾及整体并进行思考。直接后果就是,学有余力的同学会浪费宝贵的课堂时间;而学习能力较弱的同学则无法紧随教学进度。这样很难激发学生的学习兴趣,教学效率也不高,也影响整体教学效果。宋代理学家程颐总结孔子的教育思想时就已经指出:孔子教人,各因其材。儒学集大成者朱熹,一生为学,穷理及致其知,反躬以践其实,更明确地指出:圣贤施教,各因其材;小以成小,大以成大,无弃人也。于是,人们应考虑分层次教学,可以制定根据学生低年级时对高等数学和线性代数的掌握程度结合兴趣爱好和专业特点,制定一个标准,大致分成A、B和C三个等级,分别制定不同的教学进度计划、教学内容、教学目标和学时数。这样,对于自学能力强的A班同学,基础知识可以给予更深、更广的讲解。同时,引导同学们接触实践教学环节,培养其运用所学知识分析和解决实际问题的能力,在这个过程中,如果能发现问题,建立模型并较为准确地解决该问题,潜移默化中学生就发生了质的飞跃。而对于C班学生,可以适当放慢教学进度,降低教学要求,在基本知识掌握之后鼓励其多学习一些计算软件,比如Matlab、Mathematics等,在应用软件的过程中,领会所学知识点,并初步具有一定的基本技能。
三、有效改进教学手段
在矩阵分析的教学过程中,最大的忌讳莫过于照本宣科,这样做学生们无法体会所学知识的本质。但是,一本教科书、一支粉笔和一块黑板的传统教学手段非常适合重点、难点内容的“精讲”和“细讲”。一次好课,教师通过启发与讲授,循序渐进,将重点和难点讲透、讲到点子上、讲到要害处,不仅能够使学生抓住问题的本质、得到要领,而且能够引发学生进一步的思考和联想,从而提高学生的创新思维能力。教师可以将一些板书难于表达、学生难于理解和接受的复杂和抽象的内容通过多媒体演示。如在讲解“矩阵分解”时,可以将矩阵分解的几何意义结合起来。这样,教师不仅在有限的时间内传达了较多的信息,提高了课堂的教学效率,而且激发了学生学习的热情。然而,现代化教学手段的使用对于培养学生的技能及思维能力有其不足。因此,传统教学手段与现代化教学手段各有优点和不足,我们将二者结合,根据教学的目标和授课的任务,对于特定的内容,分别侧重使用现代化教学手段或传统教学手段。传统板书与现代多媒体结合,交相辉映,突出教学的重点。
四、合理安排课堂教学组织模式
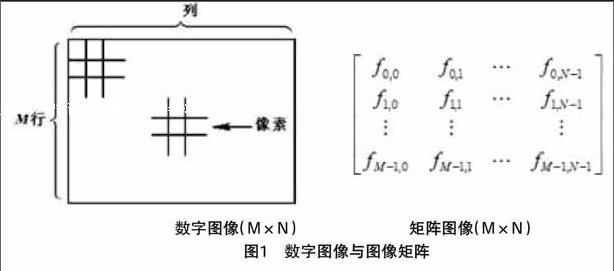
1.以问题切入知识点。一个矩阵可以表示一幅数字图像,因此数字图像可以采用矩阵分析理论及相应算法进行分析。最为直观的例子是一幅灰度图像,如图1所示。矩阵中的每一个单一元素即对应于数字图像的像素,矩阵元素的值表示该像素点的灰度值,一般取值在[0,255]。显然,这是一个M×N的矩阵,成像模型可以表示成一个线性方程组:
f=Hu+ε (1)
式中,f、u、ε∈R■(L=M×N是图像像素点个数)分别是观测数据、原始图像和加性噪声(按列展开得到的向量);H是退化因子。
数字图像处理中最广泛的图像重建问题就是已知观察数据f,根据式(1)估计出图像u,及求解方程组(1)的问题。显然,这是一个直接的矩阵计算问题。比如:方程(1)通常是一个病态问题,因此在求解时就必须考虑方程组的“病态性”问题,涉及到矩阵分析中矩阵的扰动性分析、主成分分析等;其次在求解病态方程时,涉及到最小二乘法的求解问题等相关内容;更深入地需要考虑病态方程的解的唯一性、稳定性,又涉及到矩阵分析中广义逆等。
2.理论分析后给出实例。给定一个矩阵M是一个m×n阶矩阵,其全部元素属于域K,即实数域或复数域。这样,则有如下分解:
M=UΣV*
其中Σ表示半正定的m×n阶对角矩阵;U表示m×n阶酉矩阵;而V*表示V的共轭转置,同样也是n×n阶酉矩阵。此分解我们称作M的奇异值分解。M的奇异值就是Σ对角线上的元素Σi,i。最广泛采用的方法是奇异值由大而小进行排列。这样Σ便能由矩阵M唯一确定了。(尽管U和V仍然不能确定。)为了让学生明确奇异值分解的意义,可以拿一实例图像压缩问题示范。假定一幅图像有n×n个像素点,一起传送时整个矩阵的维数太高,数据太大。因此,传输要求只传送比较少的数据,在接受终端利用比较少的数据重构复原图像。在此种思路下,如果用n×n矩阵M表示要传送的n×n个像素。那么对矩阵M首先采用奇异值分解,即得到M=UΣV*,奇异值按照由大到小排序,若从中选择k个最大的奇异值以及与之相对应的左、右奇异向量逼近原图像,这时,共用了k(2n+1)个数值代替原来的n×n个图像像素数据。这k(2n+1)个被选择的新数据是矩阵M的前k个奇异值、左奇异向量矩阵U的前k行和右奇异向量矩阵V*的前k列的元素。显然,对于绝大多数图像,通常含有较多的小奇异值时,采用此种方法可以极大降低传输量。
五、结语
矩阵分析教学过程中涉及到的方面非常多,而具体到每个方面都需要进行深入研究。它在数字图像处理及信号分析等工程应用中发挥着极其重要的作用。我们的目标是提高教学质量,使学生积极主动地掌握本专业所需的矩阵分析方法,同时培养学生逻辑能力、推理能力,学到一种理性的思维模式,以及独立获取知识的能力。
参考文献:
[1]张宝环.论大学数学教育改革[J].教育与职业,2007,(15):141-142.
[2]李刚,张新敬.普通高校大学数学分层次教学探讨[J].中州大学学报,2009,26(5):98-99.
[3]刘明月.浅谈大学数学的教学[J].学理论,2013,(36):251-252.
[4]谢凤英,赵丹培.Visual C++数字图像处理[M].北京:电子工业出版社,2008.
[5]高峰修,张春元,马智,等.工科研究生“矩阵论”课程教学研究[A].见:中国电子教育学会高教分会论文集[C].西安:中国电子教育学会高等教育分会,2012:90-92.endprint
