浅谈函数项级数的习题课设计

徐阳栋

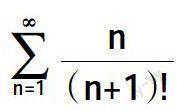
摘要：函数项级数在数学分析的内容中占有重要的位置。本文从概念的回顾、函数项级数一致收敛的判定、幂级数和函数的计算以及函数的幂级数的展开等方面来设计函数项级数及幂级数的习题课，并通过具体例子说明立体、习题精选的原则。

关键词：数学分析;函数项级数;幂级数;一致收敛性;展开式

中图分类号：O17     文献标志码：A     文章编号：1674-9324（2015）24-0178-03

数学分析是数学专业的一门非常重要的专业基础课。由于该课程中的概念抽象、逻辑性强、知识点关系紧密，因此学生在学习时往往感觉到很困难，特别是在学到级数、反常积分这几块内容时。尽管教师在课堂讲授时详细讲解了概念的内涵以及不同概念之间的关系，给出了定理的逻辑关系以及严格证明，但不少同学还是应用已学知识分析问题，遇到习题特别是一些综合性的习题还是不知从何下手。因此，在数学分析中，在习题课上安排一些重要内容还是很有必要的。习题课主要是起到学生对问题的疑问和知识巩固的作用，是课堂讲授的补充与深化。习题课的核心是总结、巩固和提升已学知识。教师应充分利用习题课帮助学生加深对概念的理解，揭示数学分析课程蕴含的丰富的数学思想，提高学生的抽象能力、逻辑推理能力、归纳总结能力和计算能力等。

本文以函数项级数为例介绍笔者在该内容习题课中的一些做法。这部分的重点是函数项级数一致收敛性的判定、幂级数和函数以及幂级数展开式的计算。

1 概念、结论、方法的回顾与总结

习题课一开始应先复习和巩固相关概念、定理和基本方法。教师在课堂上可借助提问等手段，启发学生积极思考，理清概念之间的关系。先回顾函数列、函数项级数一致收敛的定义与等价定义、判别方法及其和函数的性质，并且讨论为什么要研究函数项级数和函数的性质。同时回顾幂级数和函数以及一般函数的幂级数展开式的计算思想与方法。下面就是按照一般的函数项级数和幂级数两方面内容来分别进行总结。幂级数∑a  （x-x  ）   求 其 和 函 数S（x）？摇收敛半径R=      ？摇？摇收敛区间：（x  -R，x  +R）收敛区域：考虑收敛区间的端点解析性质？摇连续性：S（x）在（x  -R，x  +R）内连续.又若幂级数在x  -R或x  +R处收敛，则S（x）在[x  -R，x  +R）连续.可积性：S（x）在（x  -R，x  +R）内可积且幂级数可逐项积分，即      S（t）dt=      ∑a  （t-x  ）  dt=∑      a  （t-x  ）  dt=∑  （x-x  ）  可导性：S（x）在（x  -R，x  +R）内可积且幂级数可逐项求导，即  S（x）=  ∑a  （x-x  ）  =∑  a  （x-x  ）  =∑na  （x-x  ）  ？摇方法：主要利用幂级数的和函数的解析性质，四则运算和恒等变形等方法去掉系数a  ，再利用  （x-x  ）  =  公式.？摇 函 数f（x） 展 開 成 幂 级 数？摇直接方法（依赖已知函数的泰勒级数）→步骤（1）a  =  （2）形式上：    （3）讨论余项R  （x）→0，？坌x∈（x  -R，x  +R）？摇间接方法（变量代换、四则运算、恒等变形、逐项求导、逐项积分）？摇

2 几种常用函数的幂级数展开式

3 相关的练习题

为使学生更好地理解函数项级数的概念，掌握函数项级数一致收敛的判别法，熟悉幂级数和函数以及函数的幂级数展开式的计算，习题课上教师应结合这些课程的核心内容精选例题讲解、例题练习，通过让学生在黑板上做题目等方式，使学生在解题过程中感受到其中的数学方法与思想。

在常规课堂教学中，我们给出下面的例子来考查学生对上述内容的理解程度。

例1：讨论下列函数列或函数项级数在所示区间是否一致收敛。

上面的几个小例子分别可以通过函数列一致收敛的等价定义、函数项级数和函数的性质（连续性）、函数项级数的判别法（狄利克雷判别法和柯西判别法）来求解。这些例子让学生理解函数项级数的一致收敛是根据其部分和函数列的一致收敛性而来的，并且要知道函数项级数一致收敛与收敛的区别，更要掌握函数项级数的一些基本判别法。

例2：求下列幂级数的收敛半径与收敛区域。

上面两个小例子是让学生掌握幂级数的收敛半径和收敛区域的基本求法（正项级数收敛的柯西判别法）。

例3：试将下列函数按x的幂展开成幂级数。

这个例子就是要让学生熟悉并灵活应用常用函数的幂级数展开式。

例4：确定幂级数的收敛域并求和函数。

这个例子要求学生掌握并灵活幂级数和函数的性质（求导、积分符号与求和符号的交换的原则），并让学生了解在求幂级数和函数的基础上能求常数项级数的和函数，比如下面的例子。

例5：应用幂级数的性质求级数。

总之，习题课不仅要回顾、归纳、总结重要的概念和定理等内容，同时教师还应通过对习题、例题的精选、探讨、推广和总结来让学生理解解题的逻辑思维过程，感受到在求解过程中丰富的数学方法与思想，进而培养学生的计算思维、抽象思维、发散思维、逻辑推理等能力，使学生可以举一反三、融会贯通地综合运用有关的知识解决相应的问题。

参考文献：

[1]欧阳光中，朱学炎，金福临，陈传璋.数学分析[M].第三版.北京：高等教育出版社，2006.

[2]华东师范大学数学系.数学分析[M].第三版.北京：高等教育出版社，1999.

[3]陈白楷.借鉴中数教法抓好衔接延拓——“函数列和函数项级数”教学的改革初探[J].内蒙古农业大学学报（社会科学版），2007，（6）：1-3.

[4]李文赫，张彩霞，李阳.《数学分析》课程的教学改革探索与实践[J].教育教学论坛，2013，（13）：23-24.

[5]严文利.浅谈正定二次型的习题课设计[J].大学数学，2010，（26）：176-179.