基于微米压痕实验研究页岩力学特性

陈平，韩强，马天寿，林东

（油气藏地质及开发工程国家重点实验室（西南石油大学））

基于微米压痕实验研究页岩力学特性

陈平，韩强，马天寿，林东

（油气藏地质及开发工程国家重点实验室（西南石油大学））

针对页岩储集层力学特性较难获取的问题，提出基于微米力学测试技术的页岩细观力学特性定量评价方法；通过开展四川盆地长宁区块寒武系龙马溪组页岩露头的微米压痕实验，分析页岩的细观力学特性，评价宏观、细观尺度下页岩力学特性的关系。页岩微米压痕实验结果分析表明：细观弹性模量和压入硬度呈非均匀分布；宏观、细观实验对比分析显示弹性模量的细观实验统计平均值近似于宏观实验测量值。通过引入页岩组成参量——颗粒堆积密度，得到页岩组成与力学性质的关系：细观弹性模量和压入硬度随颗粒堆积密度的增加，呈非线性递增变化。基于硬度-颗粒堆积密度模型，逆向分析细观内聚力和内摩擦角，细观测量值的统计平均值略小于宏观值。微米力学测试技术可较好地表征页岩细观力学特性并有效预测宏观力学参量。图12表3参30

页岩；细观力学特性；微米压痕实验；弹性模量；压入硬度；强度参数

0 引言

目前关于页岩储集层岩石物理力学特征的研究主要参照物理与力学特性的关系，通过宏观实验（单轴/三轴强度实验）获取力学参数，选择适当的破坏准则进行分析和工程应用。宏观实验存在制样体积相对较大、实验耗时长、精度较低、个体差异性较大及对目的层精细研究效果不理想等问题[1-4]。由于页岩的特殊结构与性质，在水平段一般无法获取其完整岩心；此外，由于水平段井下工况复杂，测井仪器受测量范围制约或无法下入目的层段，导致测井资料品质不高，力学参数测量值与真实值误差较大。

进行基于微观尺度样品的压痕实验，可以逐步取代成本较高、测试耗时的单轴/三轴强度实验；在水平井或丛式井目的层段，由于现有技术取心困难，通过开展目的层段岩屑显微压痕实验评价井下岩石的实际力学参数，有利于钻井优化和井壁稳定等方面研究；在地震勘探方面，通过微尺度的孔隙模型与强度参数优化，可提升地震、测井数据的解释精度，进一步建立地震数据与岩石强度参数的联系[5-8]。

针对纳米压痕实验中存在的问题，本文基于微观力学理论和微观压痕测量原理，考虑表层微裂缝作用，

用均匀介质响应代替非均匀介质的平均响应，讨论页岩的细观力学特性。基于四川盆地长宁区块龙马溪组页岩露头的大量微米压痕实验，研究一种用于测量页岩细观力学参数的新方法，并将实验结果与宏观实验结果进行对比，分析页岩不同尺度弹性模量之间的关系；通过模型逆向分析，初步探讨细观压入硬度、强度参数和颗粒堆积密度的内在联系，并与宏观参数进行对比分析，为页岩力学分析提供新的思路。

1 微米压痕实验

1.1 实验设备

微米压痕实验采用MFT-4000多功能材料表面性能试验仪，实验载荷加载范围0.5～300.0 N、加载精度0.5 N、加载速率5～100 N/min，位移测量范围0.5～200 μm。实验压头选用等效半锥角为70.3°的玻氏压头，通过控制最大载荷与加载速度，获取载荷-位移数据。该型仪器的载荷、位移具有自校准模块，系统接触误差小于1 μm。

1.2 实验岩样

微米压痕实验岩样取自四川盆地长宁区块寒武系龙马溪组露头页岩，顺页岩层理方向切取制作岩样（尺寸：50 mm×25 mm×15 mm）。为了减小岩样表面粗糙度对实验的影响，将岩样顶底面在常温下进行机械抛光，65 ℃烘干12 h，密封备用。龙马溪组页岩多组全岩矿物X衍射分析结果表明：龙马溪组页岩石英平均含量43.4%，少见正长石与斜长石，方解石平均含量20.64%，白云石平均含量16.75%，黄铁矿平均含量1.39%；黏土矿物中伊利石含量最高，为11.98%，伊/蒙混层和绿泥石次之，含量平均值分别为2.08%和2.21%。页岩孔隙度为1.9%～9.0%，平均3.6%。实验数据及前人研究结果均表明龙马溪组页岩属于中硬—硬脆性页岩[1-2]。

1.3 实验方法

测试过程中，仪器化压入实验的关键是确定最大载荷/位移与加载速率。国外针对岩石的纳米压痕实验要求压入深度小于岩样中各相介质尺度，该方法精细但繁琐且没有考虑表层微裂缝的尺度效应，不适用于细观尺度的微米压痕实验；而金属、陶瓷等均匀材料的压痕实验标准中，压入层深度通常为已知量。本文基于国际标准ISO 14577[9]，根据龙马溪组页岩样品（上、中、下部各10块样品）在不同载荷、不同加载速率下的网格化压痕实验结果，确定实验参数。

1.3.1 最大载荷与加载速率

对多个样本组岩样进行不同载荷下的压痕实验，分析结果表明：当加载速率为15 N/min时，最大载荷为25 N和50 N的压痕点与压头自相似性较好，多数压痕点表面没有发生变形破裂；而最大载荷为75 N的压痕点，表面开始产生破坏和径向裂纹；最大载荷为100 N的压痕点，表面发生大面积崩裂，加载过程中出现脆性破坏（见图1）。岩石产生裂纹或发生破裂的过程伴随着能量损耗，若实验过程中岩石产生裂纹或破裂，将导致计算结果产生误差。

为了降低岩样表面粗糙度的影响，岩样制备过程中对表面进行了机械抛光，同时岩样表面产生变形层，导致表面发生应变硬化，机械抛光过程中使用的液态抛光剂也可能会影响岩样表面性质。国际标准ISO 14577[9]和ASTM E3-01[10]指出，实验压入深度需大于表面影响层，以尽可能消除由此产生的测量偏差。龙马溪组页岩储集层中纳米孔隙、微孔隙和微裂缝十分发育，微裂缝宽度一般为5～20 μm[1-2]。大量微米压痕实验表明，最大载荷为50 N时大部分压入深度超过40 μm，表层微裂缝对实验影响较小。基于国际标准ISO 14577[9]和页岩实际微米压痕分析，确定该实验的最大载荷为50 N。通过岩样的不同加载速率压痕实验发现：过快的加载速率导致岩样产生环向裂纹的趋势增加。加载速率越小实验效果越好，文中实验加载速率确定为10 N/min。

1.3.2 网格化压痕点设计

对于非均质的页岩材料，单个压痕点难以反映岩样的实际力学响应，需要对非均匀样本进行大量的网格化压痕实验。ISO 14577[9]规定：对非陶瓷和金属材料，相邻压痕点间距至少是最大压痕直径的10倍。在实际压痕实验中，玻氏压头相邻压入点间距通常大于20倍的压入深度。实验结果表明：岩样边部压痕点的弹性模量和压入硬度明显小于靠近对称轴的内压痕点的值。这是由于岩样制备过程中的机械加工改变了岩样的边部结构，岩样力学性质随之发生变化。确定网格化压痕点设计参数：沿岩样长轴中心线方向进行压痕实验，两压痕点间距2 mm，端部压痕点与页岩岩样边界相距9 mm（见图2）。基于上述实验原则，对取自龙马溪组露头上、中、下部的7个页岩样本组（每组3块岩样，每块岩样网格化压痕点数为20个）进行微米压痕实验，选取其中有效的300个压痕实验获取载荷-位移曲线（见图3）。实验温度保持在（24 ± 2）℃，最大载荷处压头保留时间为15 s。

图1 不同极限载荷下残余压痕的高倍光学显微照片（载荷加载速率15 N/min）

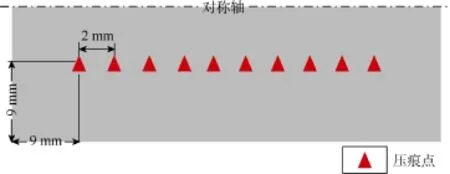
图2 网格化压痕点分布

图3 典型岩样微米压痕实验载荷-位移关系

2 分析方法

2.1 弹性模量与压入硬度

利用微米压痕技术可直接测得施加载荷和压入深度，可间接测得接触刚度、压入总功与卸载功[11-12]。目前评价材料弹性模量与硬度的方法主要有Oliver-Pharr方法[13]、做功-接触刚度方法[14]和纯压入能量方法[15]，考虑参数、系数的适用性，本文采用Oliver-Pharr方法求取弹性模量与压入硬度。

2.1.1 弹性模量

利用Oliver-Pharr方法[13]可求得接触刚度S和压入深度h。常用幂函数关系拟合卸载阶段的载荷-位移函数：

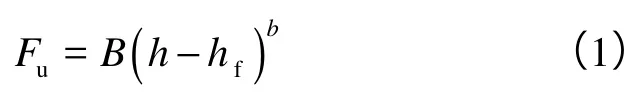
通常选取卸载曲线上部25%～50%的部分进行拟合，调整拟合范围确定出最佳拟合参数。

将（1）式在最大位移处求导，得到接触刚度：

卸载阶段的折合模量Er满足如下关系式：

其中，接触面积Ac与接触深度有关，压头在加工过程由于加工水平和使用磨损，压头尖端形状与理论设计存在差异，需要校准Ac值，较常用的校正方法包括：Oliver-Pharr方法[16]和仪器校正方法[17-18]。

①Oliver-Pharr方法[16]：通过多点、不同载荷下压入曲线进行迭代得到校准后的接触面积，其计算方法如下式：

②仪器校正方法：Sun Y等[17]提出了基于压头半径的仪器校正方法，刘东旭等[18]在此基础上，提出将尖型压头等效为球冠与圆锥的相切连接，通过有限元模拟分析给出一种确定接触面积的简便方法，其计算方法如下：

其中，接触深度满足：

Oliver-Pharr方法需要通过多次迭代求取9个拟合系数[13]，计算较为繁琐；而仪器校正方法相对简便，计算结果准确性较高，适用性更强。因此，本文采用仪器校正方法校正压头接触面积。

弹性模量E与折合模量Er关系满足：

2.1.2 压入硬度

压入硬度H定义为最大压入载荷Fm与压头接触面积Ac之比：

2.2 页岩强度特性

页岩作为多孔复合介质，具有多种矿物成分和复杂的微观结构，引入颗粒堆积密度，表征矿物组分和显微结构。根据自洽理论和堆积模型分析，颗粒堆积密度阀值η0为0.5，阀值之下颗粒无明显刚度，为力学不连续态，定义此时的弹性模量E和压入硬度H值为0；颗粒堆积密度上限为1，此时为理想态的密堆积、无孔隙[19-20]。

细观尺度下颗粒空隙率和堆积密度满足：

上述数学模型中假设细观尺度下的颗粒为球形堆积，实际实验中由于页岩存在多种矿物组分且不同矿物颗粒的大小和形状各异，使得细观条件下的η值较难获取。而在宏观尺度下η与矿物含量满足一定的关系，因此一般采用宏观尺度下的η计算值进行评价分析，如下所示。

宏观尺度下矿物含量和孔隙度满足：

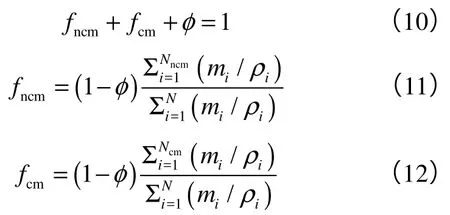
宏观尺度下颗粒堆积密度可表示为：

Cheng Y T等[21-22]采用量纲分析方法，结合有限元计算，系统探讨了压痕深度与岩样力学特性关系。

Cariou S等[23]在基质-孔隙模型和多晶颗粒堆积模型基础上，分析均匀介质的硬度-颗粒堆积密度关系，发现颗粒堆积型介质的颗粒堆积密度与页岩力学参数满足如下量纲关系：

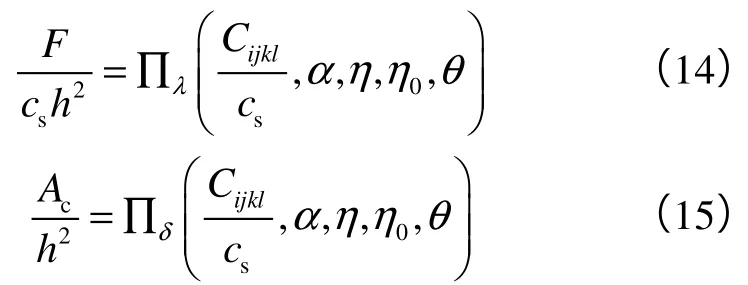
联立（14）、（15）式并与（4）式对比可得：

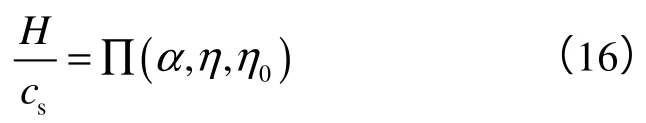
上述硬度-颗粒堆积密度关系为均匀介质的分析方法，不适用于非均质性较强的页岩，需应用强度均匀化理论对量纲函数进行均匀化处理，以满足计算要求。

Bobko C P等[24]引入颗粒接触硬度概念，给出压入硬度与强度参数的关系：

假定刚性锥形压头作用在半无限大空间，在发生塑性破坏时，细（微）观应力与材料各相的最大耗散能有关，定义平均局部耗能函数：

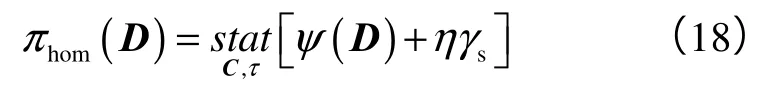
对于颗粒堆积-孔隙介质，应用Drucker-Prager准则[22,24]，将强度参数代入（18）式得到如下关系：

其中，Σ0、A、B为：

由于应力与耗散函数满足关系式：

由（19）—（21）式得到强度均匀化准则：

结合压入硬度与材料强度参数的经验公式，以及对黏性内摩擦材料的压入实验分析，由（19）式和（22）式求出对应压入深度的硬度上下限[25-28]，推导均匀化的硬度-堆积密度标度关系，在此基础上建立有限元网格化模型，求得各参数的拟合函数[23-24]。

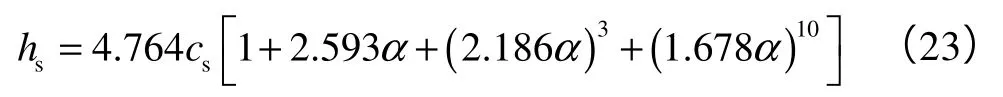
（17）式中均匀化后的量纲函数满足：

其中量纲函数∏1和∏2满足：

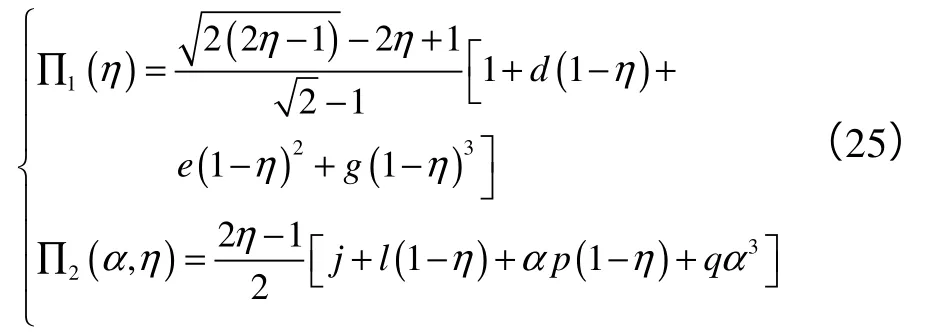
式中各系数值为：

2.3 计算及处理方法

基于微米压痕实验数据，应用Oliver-Pharr方法[13]求取弹性模量与压入硬度：根据（1）式进行卸载阶段的载荷-深度曲线拟合并判定拟合精度，求取接触刚度（（2）式）、校正接触面积（（5）式）；将接触刚度和校正接触面积代入折合模量表达式（3），根据折合模量-弹性模量关系式（7）求得细观弹性模量；将校正接触面积代入（8）式，计算压入硬度值。根据样本组的X衍射和孔隙度测定结果，计算颗粒堆积密度（（13）式），分析弹性模量-压入硬度-颗粒堆积密度关系。通过压入硬度-颗粒堆积密度关系，确定颗粒堆积密度为1的颗粒接触硬度均值并代入（17）式，结合（23）—（26）式逆向分析细观内聚力和内摩擦角。将细观力学参数与宏观实验结果进行对比分析，评价预测结果。对于测量结果，一般采用算术平均值和标准偏差的形式表示，算术平均值可近似为测量参数的真值，标准偏差表征测量值分散程度，具体测试流程见图4。

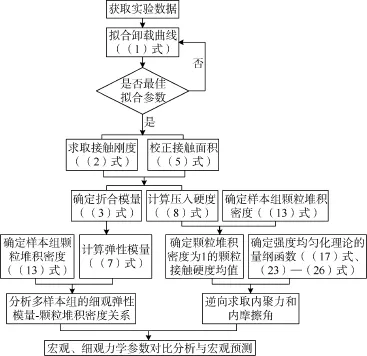
图4 细观力学参数测试与分析流程

3 结果与讨论

3.1 弹性模量、压入硬度与颗粒堆积密度

根据确定的微米压入标准，对长宁区块龙马溪组露头页岩沿层理面法线方向进行大量微米压痕实验，由（1）—（3）式、（5）—（8）式计算岩样的细观弹性模量和压入硬度。其中，已知压头常数ε为0.75，压头形状β为1.034，压头弹性模量Ei为1 140 GPa，压头泊松比vi为0.07，岩样泊松比v为0.259。

分析结果表明（见图5、图6）：细观弹性模量和压入硬度呈现非均质性，样本组弹性模量整体分布在6.0～38.7 GPa，分布在25%～75%之间的偏差小于7 GPa；压入硬度整体分布在0.18～3.61 GPa，25%～75%分布的偏差多数小于1 GPa。

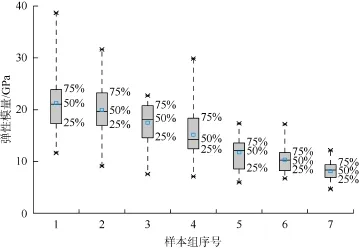
图5 各样本组细观弹性模量统计

图6 各样本组细观压入硬度统计

基于X衍射测得的页岩各矿物组分质量分数、孔隙度（见表1）及矿物密度（见表2），应用（10）—（13）式计算各样本的颗粒堆积密度。将各样本组的弹性模量和压入硬度均值化，建立与颗粒堆积密度的关系并作曲线拟合（见图7）。结果表明页岩的细观平均弹性模量、压入硬度与颗粒堆积密度呈非线性正相关关系。

表1 各样本组岩样矿物组成及孔隙度

表2 岩样矿物密度

图7 样本组平均弹性模量-平均压入硬度-堆积密度关系

3.2 页岩强度

根据图7的拟合关系，求取堆积密度为1时的细观平均颗粒接触硬度近似值，然后根据（17）式、（23）—（26）式逆向计算内摩擦系数和内聚力，求取平均值。通过等效变换，将Drucker-Prager强度准则下的强度参数变换为Mohr-Coulomb准则下的内聚力和内摩擦角，进行对比分析[24,29]（见表3）。

表3 不同强度准则下的岩样细观参数值

3.3 宏观、细观参数对比分析

以样本组1为例，讨论页岩宏观、细观尺度间力

学参数的关系。宏观实验采用RTR-1000型三轴岩石力学实验系统，对样本组1岩样进行单轴实验（实验围压0 MPa），岩样尺寸25 mm×50 mm，测得弹性模量为22.17 GPa，内聚力37.30 MPa，内摩擦角39.40°。

微米压痕实验测量结果表明，样本组1细观弹性模量呈正态分布，峰值范围20～23 GPa、平均值为21.06 GPa（见图8）。宏观、细观弹性模量比值相差较小，收敛性较好，大部分比值为0.9～1.2，平均值为1.03（见图9）。可以看出，通过微米力学测试技术能够较快、较准确地预测页岩宏观弹性模量。

图8 样本组1微米压痕实验弹性模量概率统计

图9 样本组1页岩宏观、细观弹性模量比值分布

宏观、细观内摩擦角比值为1.0～1.3，25%～75%分布的偏差小于0.1，平均值为1.15；宏观、细观内聚力的比值呈分散状分布，范围为0.6～2.96，25%～75%分布的偏差小于0.4，平均值为1.22（见图10、图11）。可见，多数样品细观内聚力、内摩擦角略小于宏观测量结果。

图10 样本组1页岩宏观、细观内摩擦角比值分布

图11 样本组1页岩宏观、细观内聚力比值分布

图12 细观弹性模量-压入硬度-压入深度关系

3.4 讨论

①在确定实验标准过程中发现，随压入载荷的增加，细观弹性模量和压入硬度与压入深度呈非线性负相关关系（见图12）。当岩样压入深度达到60 μm时，逐渐产生微裂纹；压入深度达到90 μm时，岩样表面

开始发生崩落。这是由于表层加工硬化等作用，使得样品浅表层参数值偏高；当载荷达到一定值时，岩样逐渐产生裂纹，发生能量损耗，参数值渐变减小。

②微米压痕实验表明，页岩为非均匀介质，存在明显的弹性后效作用，而物理模型没有考虑这种弹性蠕变现象，在计算过程中，压入硬度的实验值和模型计算存在偏差，可能导致细观内聚力和内摩擦角稍小于宏观测量值。

③基于Sneddon弹性解的Oliver-Pharr分析原理，仅适于压入凹陷变形[30]。根据实验测量的压入残余深度与最大深度比值K，可确定岩样的变形行为（凸起变形和凹陷变形）：受比值K和加工硬化的制约，特别当K接近于1并且加工硬化弱时，材料明显凸起；当K小于0.7时不论材料加工特性如何，几乎无凸起现象。本文实验样本组均满足K小于0.7，适用Oliver-Pharr分析理论。

4 结论

针对页岩储集层段力学特性较难获取的问题，采用微米力学测试技术，研究页岩细观弹性模量和压入硬度的分布，并结合量纲分析技术，建立定量评价页岩细观力学特性的方法。

应用弹性接触假设和微观力学理论，基于多样本组微米压痕实验数据，通过网格化压痕实验方法，设定页岩微米压痕的实验参数，对多个样本组进行微米压痕实验，结合X衍射实验与量纲分析，明确页岩组成与力学参数关系。结果表明：细观弹性模量和压入硬度呈现非均质分布，且随颗粒堆积密度的增大呈现非线性递增变化。

通过对比宏观实验和微米压痕实验结果，结合量纲函数模型，分析宏观、细观尺度下的力学特性。结果表明：宏观、细观弹性模量比值相差较小，微米压痕实验能够表征岩样的弹性模量；多数细观内摩擦角和内聚力略小于宏观值。在较难获取满足宏观实验的岩样时，微米力学测试技术可作为快速且较准确获取页岩力学参数的一种方法。文中计算模型忽略了岩石的弹性后效等作用，可通过进一步优选实验参量、细化模型属性等方法，进行修正解释。

致谢：在本文微米压痕实验过程中，西南石油大学材料科学与工程学院薛屺教授和张进老师提出了有意义的观点及建议，作者在此表示衷心感谢。

符号注释：

a——压痕半径，μm；Ac——压头接触面积，μm2；B，b，Ci，hf——拟合参数；cs——岩样的内聚力，N/μm2；C——刚度张量；Cijkl——刚度张量分量，N/μm2； D——宏观应变速率张量，无因次；Dd，Dv——宏观应变速率常量，无因次；E——弹性模量，N/μm2；Ei——压头弹性模量，N/μm2；Er——折合模量，N/μm2；fcm——黏土相体积分数，%；fncm——非黏土相体积分数，%；F——施加载荷，N；Fe——均匀化强度函数；Fm——最大载荷，N；Fu——卸载载荷，N；h——压入深度，μm；hc——接触深度，μm；hm——最大压入深度，μm；hs——η趋近于1时的颗粒接触硬度，N/μm2；H——压入硬度，N/μm2；K——压入残余深度与最大深度比值；mi——页岩中第i种矿物的质量分数，%；N——页岩中总矿物种类；Ncm——黏土相矿物种类；Nncm——非黏土相矿物种类；r——球冠压痕半径，μm；S——接触刚度，N/μm；α——岩样的内摩擦系数，无因次；β——压头形状常数，无因次；γs——非线性复合材料测定函数；ε——压头常数，无因次；η——颗粒堆积密度，无因次；η0——颗粒堆积密度阀值，无因次；θ——等效半锥角，(°)；μ，ξ——无因次孔隙形态因子； v——岩样泊松比，无因次；vi——压头泊松比，无因次；πhom(D)——局部耗能函数；∏——量纲函数；∏H——压入硬度量纲函数；∏δ——接触面积量纲函数；∏λ——压入载荷量纲函数；ρi——页岩中第i种矿物的密度，g/cm3；Σ——应力张量，N；Σd——与Dd有关的应力不变量，N；Σm——主应力均值，N；τ——预应力，N；φ——页岩孔隙度，%；φ0——空隙率，无因次；ψ(D)——线性均匀化复合材料的应变率能量函数；——静态运算函数。

[1] 王玉满,董大忠,李建忠,等.川南下志留统龙马溪组页岩气储层特征[J].石油学报,2012,33(4):551-561.Wang Yuman,Dong Dazhong,Li Jianzhong,et al.Reservoir characteristics of shale gas in Longmaxi Formation of the Lower Silurian,southern Sichuan[J].Acta Petrolei Sinica,2012,33(4):551-561.

[2] 马天寿,陈平.基于CT扫描技术研究页岩水化细观损伤特性[J].石油勘探与开发,2014,41(2):227-233.Ma Tianshou,Chen Ping.Study of meso-damage characteristics of shale hydration based on CT scanning technology[J].Petroleum Exploration and Development,2014,41(2):227-233.

[3] 崔思华,班凡生,袁光杰.页岩气钻完井技术现状及难点分析[J].天然气工业,2011,31(4):72-75.Cui Sihua,Ban Fansheng,Yuan Guangjie.Status quo and challenges of global shale gas drilling and completion[J].Natural Gas Industry,2011,31(4):72-75.

[4] 王红岩,刘玉章,董大忠,等.中国南方海相页岩气高效开发的科学问题[J].石油勘探与开发,2013,40(5):574-579.Wang Hongyan,Liu Yuzhang,Dong Dazhong,et al.Scientific issues on effective development of marine shale gas in southern China[J].Petroleum Exploration and Development,2013,40(5):574-579.

[5] Ortega J A,Ulm F J,Abousleiman Y.The effect of the nanogranular nature of shale on their poroelastic behavior[J].Acta Geotechnica,2007,2(3):155-182.

[6] Constantinides G,Chandran K S R,Ulm F J,et al.Grid indentation analysis of composite microstructure and mechanics:Principles and validation[J].Materials Science and Engineering:A,2006,430(1):189-202.

[7] Dormieux L,Molinari A,Kondo D.Micromechanical approach to the behavior of poroelastic materials[J].Journal of the Mechanics and Physics of Solids,2002,50(10):2203-2231.

[8] Chateau X,Dormieux L.Micromechanics of saturated and unsaturated porous media[J].International Journal for Numerical and Analytical Methods in Geomechanics,2002,26(8):831-844.

[9] International Organization for Standards.ISO 14577 Metallic materials:Instrumented indentation test for hardness and materials parameters-Part 1:Test method[S].Geneva,Switzerland:International Organization for Standards,2002.

[10] ASTM.ASTM E3:Standard guide for preparation of metallographic specimens[S].West Conshohocken:ASTM,2007.

[11] 张泰华.微/纳米力学测试技术及其应用[M].北京:机械工业出版社,2004:71-108.Zhang Taihua.Micro/nano mechanical testing technology and application[M].Beijing:China Machine Press,2004:71-108.

[12] 张泰华.微/纳米力学测试技术[M].北京:科学出版社,2013:111-157.Zhang Taihua.Micro/nano mechanical testing technology[M].Beijing:Science Press,2013:111-157.

[13] Oliver W C,Pharr G M.An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments[J].Journal of Materials Research,1992,7(6):1564-1583.

[14] Cheng Y T,Cheng C M.Relationships between hardness,elastic modulus,and the work of indentation[J].Applied Physics Letters,1998,73(5):614-616.

[15] Ma D,Ong C W,Wong S F,et al.New method for determining Young’s modulus by non-ideally sharp indentation[J].Journal of Materials Research,2005,20(06):1498-1506.

[16] Pharr G M,Oliver W C,Brotzen F R.On the generality of the relationship among contact stiffness,contact area,and elastic modulus during indentation[J].Journal of Materials Research,1992,7(3):613-617.

[17] Sun Y,Zheng S,Bell T,et al.Indenter tip radius and load frame compliance calibration using nanoindentation loading curves[J].Philosophical Magazine Letters,1999,79(9):649-658.

[18] Liu D X,Zhang T H.An new area function for sharp indenter tips in nanoindentation[J].Chinese Journal of Aeronautics,2004,17(3):159-164.

[19] Sherwood J D.Packing of spheroids in three-dimensional space by random sequential addition[J].Journal of Physics A:Mathematical and General,1997,30(24):L839.

[20] Sanahuja J,Dormieux L,Chanvillard G.Modelling elasticity of a hydrating cement paste[J].Cement and Concrete Research,2007,37(10):1427-1439.

[21] Cheng Y T,Cheng C M.Scaling,dimensional analysis,and indentation measurements[J].Materials Science and Engineering,2004,44(4):91-149.

[22] Ortega J A,Gathier B,Ulm F J.Homogenization of cohesive-frictional strength properties of porous composites:Linear comparison composite approach[J].Journal of Nanomechanics and Micromechanics,2011,1(1):11-23.

[23] Cariou S,Ulm F J,Dormieux L.Hardness-packing density scaling relations for cohesive-frictional porous materials[J].Journal of the Mechanics and Physics of Solids,2008,56(3):924-952.

[24] Bobko C P,Gathier B,Ortega J A,et al.The nanogranular origin of friction and cohesion in shale:A strength homogenization approach to interpretation of nanoindentation results[J].International Journal for Numerical and Analytical Methods in Geomechanics,2011,35(17):1854-1876.

[25] Chitkara N R,Butt M A.Numerical construction of axisymmetric slip-line fields for indentation of thick blocks by rigid conical indenters and friction at the tool-metal interface[J].International Journal of Mechanical Sciences,1992,34(11):849-862.

[26] Lockett F J.Indentation of a rigid/plastic material by a conical indenter[J].Journal of the Mechanics and Physics of Solids,1963,11(5):345-355.

[27] Ganneau F P,Constantinides G,Ulm F J.Dual-indentation technique for the assessment of strength properties of cohesive-frictional materials[J].International Journal of Solids and Structures,2006,43(6):1727-1745.

[28] Borges L A,Zouain N,Huespe A E.A nonlinear optimization procedure for limit analysis[J].European Journal of Mechanics Series A/Solids,1996,15(3):487-512.

[29] Schweiger H F.On the use of drucker-prager failure criteria for earth pressure problems[J].Computers and Geotechnics,1994,16(3):223-246.

[30] Oliver W C,Pharr G M.Measurement of hardness and elastic modulus by instrumented indentation:Advances in understanding and refinements to methodology[J].Journal of Materials Research,2004,19(1):3-20.

（编辑 魏玮 王大锐）

The mechanical properties of shale based on micro-indentation test

Chen Ping,Han Qiang,Ma Tianshou,Lin Dong
(State Key Laboratory of Oil &Gas Reservoir Geology and Exploitation,Southwest Petroleum University,Chengdu 610500,China)

In view of the difficulty to get mechanical characteristics of shale reservoirs,a quantitative evaluation method based on micro-indentation test technology was proposed to research the meso-mechanical properties of shale.Through micro-indentation test of shale outcrop samples from the Cambrian Longmaxi Formation in the Changning area,Sichuan Basin,the meso-mechanical properties of shale were analyzed,and the relationship between the macro-scale and meso-scale shale mechanical properties was evaluated.The analysis results of micro-indentation tests show that the mesoscopic elastic modulus and indentation hardness are heterogeneous in distribution.The comparison of macro and meso experiments shows that the statistical mean value of meso-elastic modulus is approximate to the value of the macro-elastic modulus.The relationship between composition and mechanical properties of shale was obtained based on the packing density model theory.The result shows that mesoscopic elastic modulus and indentation hardness increase nonlinearly with the increase of the packing density.Based on the hardness-packing density model,the reverse analysis of cohesion and friction angles shows that the mesoscopic value is slightly smaller than the macroscopic value.The micro-indentation test technology can evaluate shale meso-mechanical properties and predict the macro-mechanical properties effectively.

shale;meso-mechanical property;micro-indentation test;elastic modulus;indentation hardness;strength parameters

国家重点基础研究发展计划（973）项目“页岩气水平井钻完井关键基础研究”（2013CB228003）

TE135

A

1000-0747(2015)05-0662-09

10.11698/PED.2015.05.15

陈平（1952-），男，四川成都人，西南石油大学教授，主要从事定向井、丛式井、水平井、侧钻水平井等钻井技术研究。地址：四川省成都市新都区新都大道8号，西南石油大学，邮政编码：610500。E-mail：chenping@swpu.edu.cn

联系作者：韩强（1985-），男，陕西咸阳人，现为西南石油大学石油与天然气工程学院博士研究生，主要从事页岩钻井井壁稳定与随钻测量技术方面的研究工作。地址：四川省成都市新都区新都大道8号，西南石油大学科技园大厦1008室，邮政编码：610500。E-mail：hqcampus@163.com

2014-10-16

2015-07-30