压裂投产低—特低渗透油藏井排距设计

卞晓冰，张士诚，张景臣，汪道兵

（1.中国石油化工股份有限公司石油工程技术研究院；2.中国石油大学（北京））

压裂投产低—特低渗透油藏井排距设计

卞晓冰1,2，张士诚2，张景臣2，汪道兵2

（1.中国石油化工股份有限公司石油工程技术研究院；2.中国石油大学（北京））

为了模拟压裂投产低—特低渗透油藏中的非达西渗流特征，在原有黑油模拟器的基础上，建立并求解了考虑两相启动压力梯度、渗透率敏感性以及裂缝导流能力失效性的三维两相数值模拟模型，基于模型分析了压裂井波及椭圆的计算方法及影响因素，并推导了矩形井网和菱形反九点井网的井排距公式。压裂井波及椭圆影响因素分析结果表明：渗透率对压裂水井初期的波及椭圆大小具有显著影响，随着时间的增加注入压差和启动压力影响增大；各因素对波及椭圆的形状没有显著影响。通过遗传算法改进的GA-BP神经网络模型可准确求取压裂井波及椭圆参数。为实现井网系统和裂缝系统的最优匹配，以压裂井对油藏波及系数最大为目标，推导了矩形井网和菱形反九点井网的井排距公式。现场应用表明，压裂后平均日产油量可提高1.25倍，且长期增产效果显著。图5表3参18

低—特低渗透油藏；压裂井；波及椭圆；井排距设计

0 引言

大量开发实例表明，低—特低渗透油田具有产能递减快、注水效果差、见水后油井含水率急剧上升、最终采收率低的特点[1-2]，应用经典达西定律已不能对低渗透油田的开发效果作出合理解释。由于低—特低渗透油藏具有比中高渗油藏更细小的孔隙和喉道[3-4]，流体在其中流动时会受到除黏滞阻力之外的附加渗流阻力，从而表现出非达西渗流特征。低—特低渗透油田多采用压裂后投产的方式，研究表明，压裂井（油、水井）生产时的等势线是以井点为中心的椭圆簇[5-6]。目前部分学者提出了地层参数、压裂井生产制度及裂缝参数等因素对压裂井波及椭圆的影响规律，并以波及椭圆为基础进行井网部署优化[7-8]，但研究井别主要针对生产井，且关于低—特低渗透地层非达西渗流特征及人工裂缝生产失效性等因素进行的研究较少，因此不可避免会对低—特低渗透油田开发产生影响。笔者基于文献[9]建立的三维两相油藏数值模型，研究包括低—特低渗透地层非达西渗流特征在内的多因素对压裂井波及椭圆的影响，并推导矩形井网和反九点井网的井排距计算公式。

1 基础渗流模型

黑油模型在油藏动态模拟方面已有广泛应用[9-10]。

本文在原有黑油模拟器的基础上，引入非达西渗流数学模型，进行适应低—特低渗透油藏压裂井生产特性的功能扩展。启动压力梯度及受应力敏感效应影响的渗透率敏感系数的常用表达式[11-12]为：

同时，考虑裂缝长期导流能力随时间变化的指数函数表达式[13]如下：

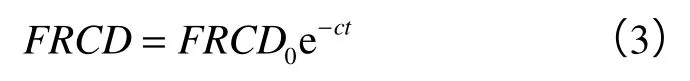
联立基础黑油模型及（1）—（3）式，通过IMPES算法实现压裂井非达西渗流模型的建立和求解[14]。以此为基础进行了大量数值模拟计算，用以研究地层及裂缝参数对压裂井波及椭圆的影响。

2 压裂井波及椭圆的影响因素及求取方法

压裂井波及椭圆的大小和形状与诸多因素有关[7]。计算中用垂直裂缝方向的椭圆短半轴长代表受裂缝影响程度最小的地层压力波的传播距离；椭圆长短轴之比则代表了椭圆的形状，为受裂缝影响最大和最小的压力传播距离的比值，可清楚识别裂缝的存在对压力传播范围变形程度的影响。根据椭圆的短半轴长及长短轴之比可确定椭圆大小。

2.1 压裂井波及椭圆影响因素分析

多孔介质、流体性质和流动状况是决定流体渗流规律的三大影响因素[14]，因此选取代表以上三要素的3个参数：K、μL、Δp，两个裂缝参数：Lf和FRCD，以及3个非达西渗流特征参数：GL、α和c，一共8个参数对压裂井波及椭圆进行单因素敏感性分析。选用的数值模拟基础参数为：地层渗透率2.55×10−3μm2，地层孔隙度16.5%，地层有效厚度6.7 m，原始含水饱和度50.9%，地层水黏度0.4 mPa·s，地层油黏度3.3 mPa·s，地层油密度642 kg/m3，地层油体积系数1.585 7 m3/m3，地层油压缩系数0.002 243 MPa−1，地层水压缩系数0.000 486 MPa−1，岩石压缩系数0.004 MPa−1，原始油藏压力31.58 MPa，生产压差5 MPa，井筒半径0.1 m。

以水相启动压力梯度为例，探讨其对压裂水井波及椭圆的影响。水相启动压力梯度取值范围：0.002～0.100 MPa/m，其对单裂缝波及椭圆短半轴长和长短轴之比的影响见图1，可见：启动压力梯度对椭圆短半轴长和长短轴之比均有较大的影响，水相启动压力梯度越大，椭圆短半轴长越小，且长短轴之比越大。除了黏滞阻力之外，启动压力是地层流体受到的另一主要阻力，因此启动压力梯度越大压力波传播速度越慢。

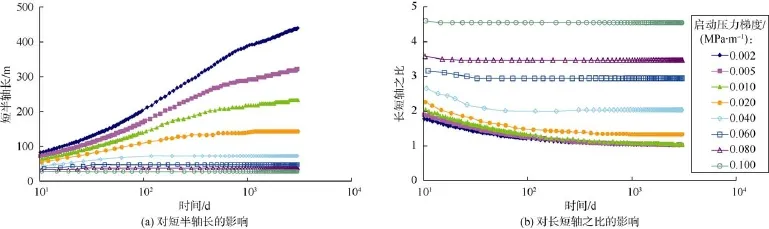
图1 水相启动压力梯度对压裂井波及椭圆的影响

若水相启动压力梯度足够小，达到某一下限，启动压力梯度对椭圆长短轴之比的影响可忽略不计，且趋于稳定的长短轴之比近似为1；若启动压力梯度足够大达到某一上限，由于流体从初始时刻就很难流动，椭圆很快便趋向于拟稳定状态，其形状和大小受时间的影响都比较小。

2.2 正交方案设计及方差分析

以注水井为例，对以下8个单因素：K、μw、Δp、Lf、FRCD、Gw、α、c，根据单因素敏感性分析结果选取对压裂水井波及椭圆影响最大的4个水平值，设计出8因素4水平的正交方案表，各正交设计方案生产第1年、第2年和第3年对应的注水井波及椭圆短半轴长和长短轴之比计算结果见表1。以此为基础进行方差分析，即可对各因素的影响程度进行排序（见表2）。

从表2可以看出，在水井注入初期，表征油藏属性的K对椭圆短半轴长和长短轴比起决定性作用，但由于μw变化范围远小于μo，因而表征流体属性的μw

对椭圆短半轴长的影响程度逐年递减，且μw对长短轴之比的影响在所有因素中最小；随着注入时间的增加，椭圆短半轴长和长短轴比受驱动力和阻力的影响开始增加，Δp和Gw开始成为主要的影响因素。但对于注水井而言，Lf不是长短轴比最显著的影响因素；且各因素对于长短轴比的影响均不显著。

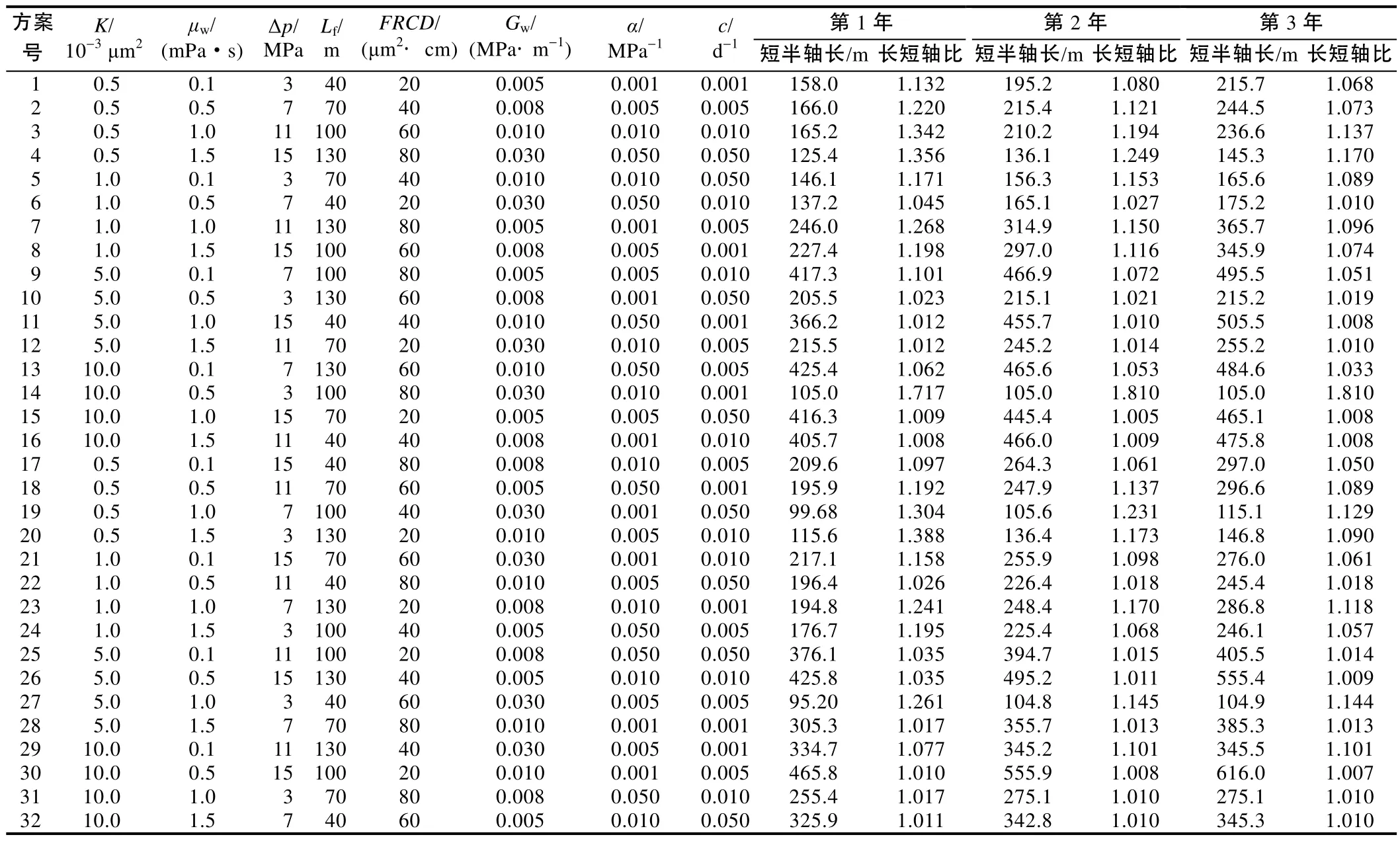
表1 压裂水井波及椭圆影响因素正交方案设计及计算结果

表2 压裂水井波及椭圆短半轴长和长短轴比影响因素排序

因此，对压裂注水井提出以下建议：与油井相比，可以对注水井设计相对较小的缝长；由于水相启动压力梯度对波及区域影响较大，因此需要及早采取大压差进行注入。

2.3 压裂井波及椭圆求取

GA-BP神经网络将遗传算法和神经网络结合起来，采取遗传算法优化得到神经网络的初始化参数，使得初始点接近全局最优点，这样就可以使网络更快更准确地收敛于全局最优解[15]。选用Matlab的遗传算法GAOT工具箱[16]及BP神经网络工具箱，可以方便地实现用GA-BP神经网络[17]处理得到所需的工程结果。

以单因素分析模拟的289个压裂油、水井波及椭圆短半轴长和长短轴比数据为样本参数，正交方案中最后10个作为测试样本单独拿出，应用GA-BP神经网络预测不同参数条件下对应的压裂油、水井波及椭圆短半轴长和长短轴比。

以水井为例，输入数据为K、μw、Δp、Lf、FRCD、Gw、α、c；输出数据共6个，为第1年、第2年和第3年的波及椭圆短半轴长和长短轴比。因此网络输入层节点数为8，输出层节点数为6。构建1个两层神经网络，设置种群规模为100，遗传代数为1 000。把遗传算法优化出的神经网络权值和阈值赋给尚未开始训练的BP网络，学习和训练17次后满足训练目标误差0.001（见图2）。用测试样本来验证所建立GA-BP神经网络的准确性，第1年的10个方案作为样本测试方案，将模型预测的椭圆短半轴长和长短轴比与实际计算结果对比（见图3），可以看出预测值与计算值吻合得较好。因此所建立模型具有较高精度，可以用来预测不同输入参数条件下的椭圆短半轴长和长短轴比。

3 规则井网井排距的确定

为了最大程度地动用区块储量，同时能合理地利

用地层本身的能量与注水能量，以投产1 a时的压裂井波及椭圆相切且尽可能紧密排列为基础进行井网部署，以达到井网系统和裂缝系统最优匹配的目的。

图2 训练误差曲线图

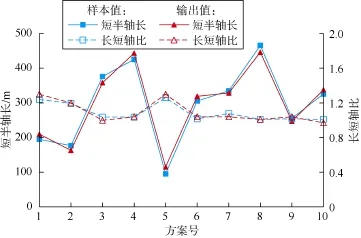
图3 10个测试样本方案生产第1年波及椭圆尺寸网络输出结果验证曲线

图4为矩形井网示意图，基本井网单元如矩形粗实线区域所示。在矩形区域内，以两口生产井波及椭圆切点为原点建立直角坐标系，其中生产井波及椭圆长、短半轴长分别为a1、b1，注水井波及椭圆长、短半轴长分别为a2、b2。

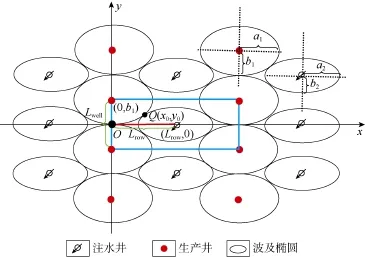
图4 矩形井网示意图

令排距为Lrow，则注水井波及椭圆中心坐标为(Lrow，0)，过第1、2象限的生产井中心坐标为(0，b1)，此两口井波及椭圆的切点坐标设为Q(x0，y0)。则过切点Q切线的斜率可表示为：

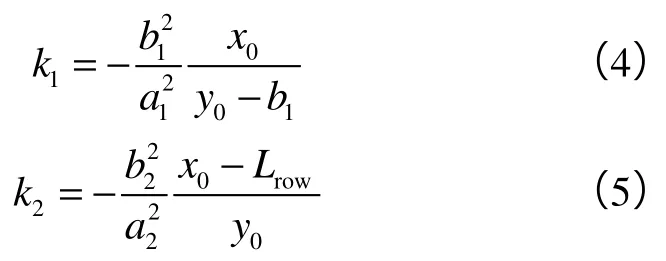
由于此两椭圆相切，故k1=k2，则：

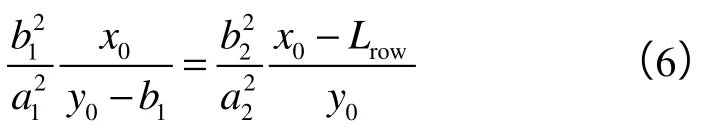
又因切点Q同时位于两椭圆上，根据椭圆标准式可得：

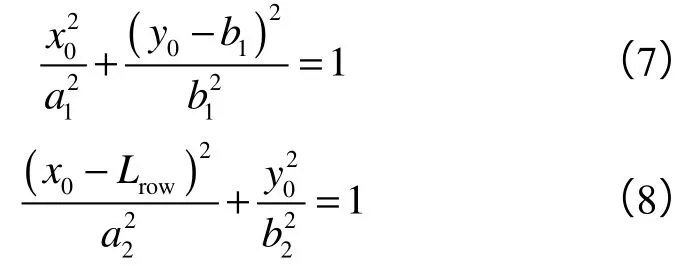
（6）式可变形为：

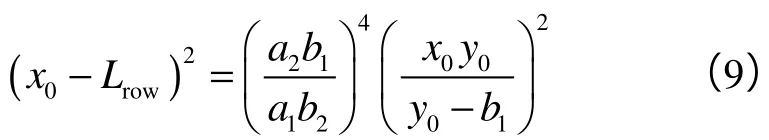
将（9）式代入（8）式整理得：

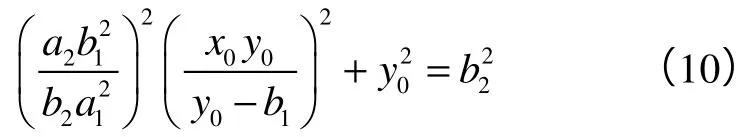
将（7）式变形为：

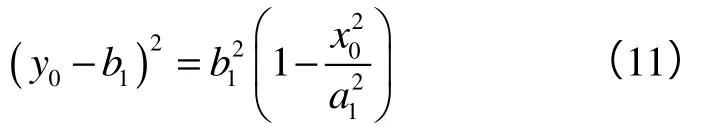
将（11）式代入（10）式即可求得：

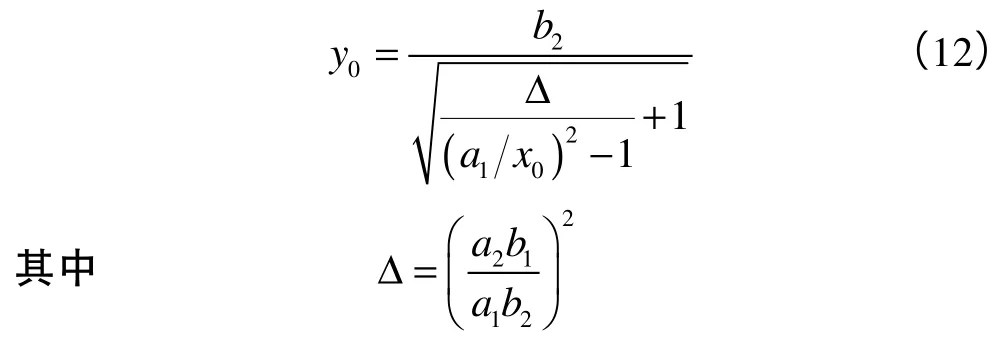
将（12）式代入（7）式，简化得：

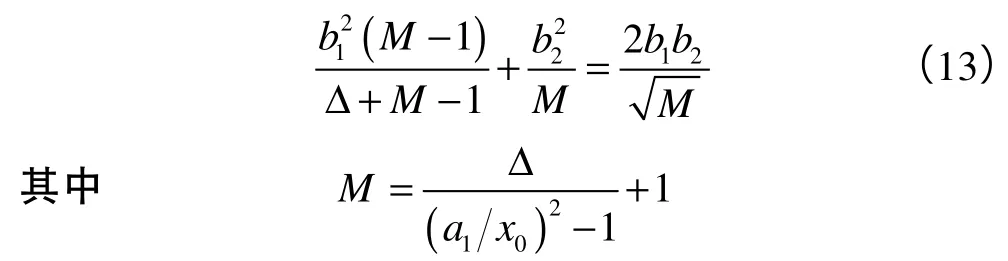
对（13）式两边求平方，整理后为关于M的一元四次方程，见（14）式，其正实根可通过费拉里（Ferrari）解法[18]求得。

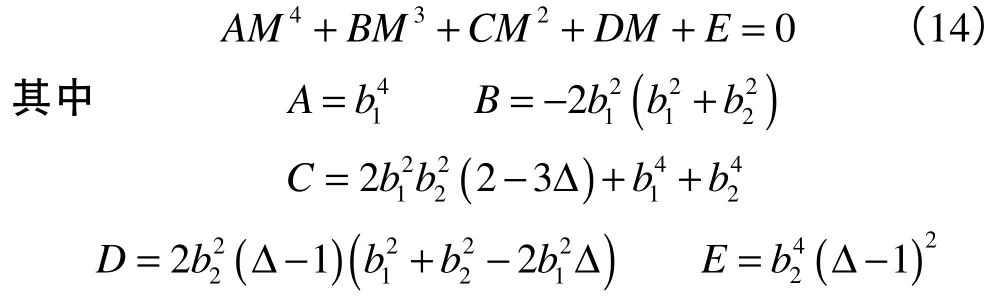
求出M后，即可联立（6）式、（12）式和（13）式求出x0、y0和排距Lrow，显然有井距Lwell=2b1，根据Lwell和Lrow即可求得矩形井网各井点的位置。

图5为菱形反九点井网示意图，基本井网单元如菱形粗实线区域所示，井网单元中相邻生产井波及椭圆两两相切，且边井R2和R3相切于点O′（对称位置两口边井波及椭圆亦然），易知，菱形的大小和形状仅与生产井波及椭圆形状有关。

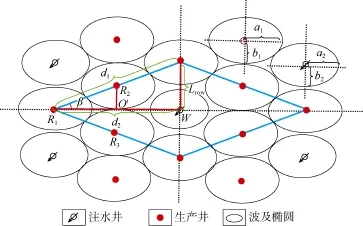
图5 菱形反九点井网示意图

此时菱形反九点井网井排距优化问题即转化为注水井波及椭圆的求取问题，要求注水井波及椭圆与相邻角井及边井的波及椭圆不存在相离的情况，此时与其相邻的生产井都能受效。判别条件如下：

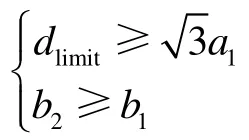
其中dlimit为注水井波及椭圆与两口边井波及椭圆相切时水井中心点与两口边井切点之间的距离，可由（4）—（14）式求得。

4 应用实例

柴达木盆地某低渗透WN区块储集层埋深为1 300 m，地质储量约6.8×106t，油藏物性具有低—特低渗的特征。目的层厚15 m，平均渗透率为5×10−3μm2，地层油黏度4.35 mPa·s、体积系数1.246，地层水黏度0.95 mPa·s，原始地层压力17.8 MPa。WN区块于2002年开始进行滚动开发，至2007年底共投产87口井（其中7口水井）。油田主要措施以补孔为主，经过几年的试采生产，大部分油井产量递减较快。为了进一步提高WN区块的开发效果，拟进行井间加密并调整为菱形反九点井网生产。应用本文所建立的GA-BP神经网络系统进行不同裂缝参数条件下的油、水井波及椭圆大小及形状预测，非达西渗流特征参数通过室内实验回归得到（1）式—（3）式中的a为0.012、b为1.063，α为0.053 MPa−1，c为0.003 5 d−1。模拟优化结果表明水井半缝长50～60 m、油井半缝长80～90 m、导流能力20～30 μm2·cm时，油、水井波及椭圆面积出现临界值，此时油井波及椭圆长、短半轴长分别为170～210 m和110～130 m，水井波及椭圆长、短半轴长分别为160～195 m和140～170 m。由（4）式—（18）式可确定排距Lrow为220～260 m，角井间距离d1为627～772 m，水井和角井间距离d2为588～727 m。WN区块于2008年现场试验了6口井，压裂后平均日产油量提高了1.25倍（见表3）。投产3 a后平均单井日产油量仍保持在2.6 t/d，长期稳产效果显著。

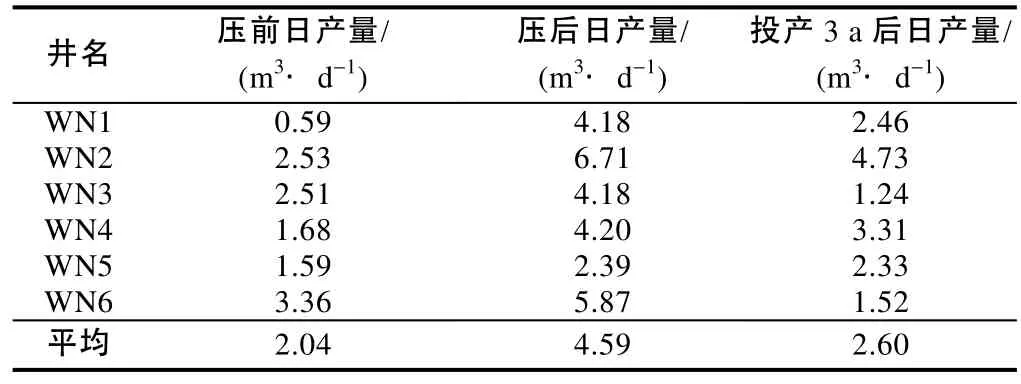
表3 压裂前后油井日产量数据对比

5 结论

在原有压裂井黑油模型基础上，考虑了低渗透油藏启动压力梯度、地层应力敏感性及人工裂缝导流能力失效性的影响，用以模拟低渗透油藏压裂井非达西渗流特征。敏感性分析结果表明，在水井注入初期，表征油藏属性的K对压裂井波及椭圆形状和大小起决定性作用，其次是Δp、Gw；随着注入时间的增加，Δp和Gw成为主要影响因素；各因素对于长短轴之比的影响均不显著。建立了用遗传算法改进的GA-BP神经网

络模型，可快速计算压裂油、水井波及椭圆的大小。对于给定的油藏流体参数、裂缝参数和井控参数，可方便地求出其波及椭圆；以压裂井波及系数最大为目标，推导了矩形井网和菱形反九点井网的井排距解析式。应用本文方法对特低渗透油藏WN区块进行了菱形反九点井网调整部署，现场试验6口井，长期增产效果显著。

符号注释：

a，b——计算启动压力梯度的相应实验回归系数，无因次；a1，b1——生产井波及椭圆长、短半轴长，m；a2，b2——注水井波及椭圆长、短半轴长，m；c——裂缝导流能力失效系数，d−1；d1，d2——菱形反九点井网基本单元的角井距离、角井和注水井距离，m；dlimit——菱形反九点井网注水井波及椭圆与两口边井波及椭圆相切时水井中心点与两口边井切点之间的距离，m；FRCD，FRCD0——裂缝导流能力及初始导流能力，μm2·cm；GL——液相的启动压力梯度，MPa/m；Gw——水相的启动压力梯度，MPa/m；K，K0——地层渗透率及初始渗透率，10−3μm2；k1——与生产井波及椭圆相切于Q点的切线的斜率，无因次；k2——与注水井波及椭圆相切于Q点的切线的斜率，无因次；Lf——裂缝半长，m；Lrow——排距，m；Lwell——井距，m；——菱形反九点井网两口边井切点与菱形中心点之间的距离，m；p，p0——地层压力及初始地层压力，MPa；Δp——生产压差，MPa；——菱形反九点井网基本单元中角井和边井中心点的距离，m；t——时间，d；α——渗透率敏感系数，MPa−1；β——菱形的一条边与椭圆长轴方向的夹角，（°）；μL——流体黏度，mPa·s；μo——原油黏度，mPa·s；μw——水黏度，mPa·s。

[1] 胡文瑞.中国低渗透油气的现状与未来[J].中国工程科学,2009,11(8):29-37.Hu Wenrui.The present and future of low permeability oil and gas in China[J].Engineering Science,2009,11(8):29-37.

[2] 袁自学,王靖云,李淑珣,等.特低渗透注水砂岩油藏采收率确定方法[J].石油勘探与开发,2014,41(3):341-348.Yuan Zixue,Wang Jingyun,Li Shuxun,et al.A new approach to estimating recovery factor for extra-low permeability water-flooding sandstone reservoir[J].Petroleum Exploration and Development,2014,41(3):341-348.

[3] 胡罡.计算水驱油藏体积波及系数的新方法[J].石油勘探与开发,2013,40(1):103-106.Hu Gang.A new method for calculating volumetric sweep efficiency in a water-flooding oilfield[J].Petroleum Exploration and Development,2013,40(1):103-106.

[4] Zhang J C,Bian X B.Numerical simulation of hydraulic fracturing coal bed methane reservoir with independent grid[J].Fuel,2015,143:543-546.

[5] 曾保全,程林松,李春兰,等.特低渗透油藏压裂水平井开发效果评价[J].石油学报,2010,31(5):791-796.Zeng Baoquan,Cheng Linsong,Li Chunlan,et al.Development evaluation of fractured horizontal wells in ultra-low permeability reservoirs[J].Acta Petrolei Sinica,2010,31(5):791-796.

[6] Gupta A D,Xie J,Gupta N,et al.Radius of investigation and its generalization to unconventional reservoirs[J].Journal of Petroleum Technology,2011:52-55.

[7] 甘云雁,张士诚,陈利,等.复杂断块油藏不规则井网整体压裂优化设计[J].石油学报,2006,27(4):81-84.Gan Yunyan,Zhang Shicheng,Chen Li,et al.Optimization design of integral hydraulic fracturing for skewed patterns in low-permeability complex faulted reservoir[J].Acta Petrolei Sinica,2006,27(4):81-84.

[8] Zhang J C.Numerical simulation of hydraulic fracturing coalbed methane reservoir[J].Fuel,2014,136:57-61.

[9] 卞晓冰,张士诚,马新仿,等.考虑非达西流的低渗透油藏水力压裂优化研究[J].中国石油大学学报:自然科学版,2012,36(3):115-120.Bian Xiaobing,Zhang Shicheng,Ma Xinfang,et al.Optimization of hydraulic fracturing considering non-Darcy flow in low permeability reservoirs[J].Journal of China University of Petroleum:Natural Science Edition,2012,36(3):115-120.

[10] Bian X B,Zhang S C,Zhang J C,et al.A new method to optimize the fracture geometry of a frac-packed well in unconsolidated sandstone heavy oil reservoirs[J].Science China Technological Sciences,2012,55(6):1725-1731.

[11] 郝斐,程林松,李春兰,等.特低渗油藏启动压力梯度研究[J].西南石油学院学报,2006,28(6):29-33.Hao Fei,Cheng Linsong,Li Chunlan,et al.Study on threshold pressure gradient in ultra-low permeability reservoir[J].Journal of Southwest Petroleum Institute,2006,28(6):29-33.

[12] 戈尔布诺夫.异常油田开发[M].章树宝,译.北京:石油工业出版社,1987.Gorbunov А.Т.Abnormal oil-field development[M].Zhang Baoshu,Trans.Beijing:Petroleum Industry Press,1987.

[13] 温庆志,蒲春生,曲占庆,等.低渗透、特低渗透油藏非达西渗流整体压裂优化设计[J].油气地质与采收率,2009,16(6):102-104.Wen Qingzhi,Pu Chunsheng,Qu Zhanqing,et al.Integral fracturing optimization design of non-Darcy flows in low and untra-low permeability oil reservoirs[J].Petroleum Geology and Recovery Efficiency,2009,16(6):102-104.

[14] 吴柏志.低渗透油藏高效开发理论与应用[M].北京:石油工业出版社,2009.Wu Bozhi.Efficient development theory and application of the low permeability reservoir[M].Beijing:Petroleum Industry Press,2009.

[15] 陈秋莲,王成栋.基于Matlab遗传算法工具箱的优化计算实现[J].现代电子技术,2007,2:124-126.Chen Qiulian,Wang Chengdong.Optimization of genetic algorithm toolbox based on matlab[J].Modern Electronic Technology,2007,2:124-126.

[16] 可华明,陈朝镇,张新合,等.遗传算法优化的BP神经网络遥感图像分类研究[J].西南大学学报:自然科学版,2010,32(7):128-132.Ke Huaming,Chen Zhaozhen,Zhang Xinhe,et al.Study on BP neural network classification with optimization of genetic algorithm for remote sensing imagery[J].Journal of Southwest University:Natural Science Edition,2010,32(7):128-132.

[17] 冯冬青,李卫帅.基于GA-BP神经网络的电池剩余电量的预测[J].计算机仿真,2011,28(12):323-326.Feng Dongqing,Li Weishuai.Prediction of residual capacity for battery based on GA-BP neural network[J].Computer Simulation,2011,28(12):323-326.

[18] 郭敏.一元四次方程公式解的追根溯源[J].数学之友,2011,12:72-73.Guo Min.Tracing origins for the formula solution of one basic quartic equation [J].Friends of Math,2011,12:72-73.

（编辑 张敏 胡苇玮）

Well spacing design for low and ultra-low permeability reservoirs developed by hydraulic fracturing

Bian Xiaobing1,2,Zhang Shicheng2,Zhang Jingchen2,Wang Daobing2
(1.Sinopec Research Institute of Petroleum Engineering,Beijing 100101,China;2.China University of Petroleum(Beijing),Beijing 102249,China)

In order to simulate non-Darcy flows in low and ultra-low permeability reservoirs,based on the black oil simulator,a three-dimensional,two-phase model was established considering two-phase start-up pressure,permeability sensibility and fracture conductivity decline.Then numerous simulations were run to analyze the elliptic drainage area induced by a fractured well,the results show that:for water fractured well,permeability is the dominant factor affecting the elliptic drainage area at the beginning,and pressure difference and start-up pressure have increasing effects as time goes by.However,no factor has a marked impact on the shape of elliptic drainage area.Parameters of elliptic drainage area can be calculated with GA-BP neural network improved by genetic algorithm.Aiming at acquiring maximum sweep efficiency,well spacing equations were deduced for rectangular pattern and diamond inverted nine-spot pattern.Field application demonstrated daily oil production enhanced 1.25 times after hydraulic fracturing,and the long time stimulation effect is substantial.

low and ultra-low permeability reservoir;fractured well;elliptic drainage area;well spacing design

国家科技重大专项“3000型成套压裂装备研制及应用示范工程”（2011ZX05048）

TE357.1

A

1000-0747(2015)05-0646-06

10.11698/PED.2015.05.12

卞晓冰（1985-），男，山东菏泽人，博士，中国石油化工股份有限公司石油工程技术研究院工程师，主要从事水力压裂优化设计、油气藏数值模拟方面的研究工作。地址：北京市朝阳区北辰东路8号，中国石油化工股份有限公司石油工程技术研究院，邮政编码：100101。E-mail：xiaobingbian@126.com

2014-12-16

2015-06-12