自升式平台桩腿强度对弦管间距敏感性分析

朱亚洲，孙承猛，张晓宇，戚欣，秦洪德，姜滨

（1.哈尔滨工程大学船舶工程学院；2.中国石油集团渤海装备辽河重工有限公司）

自升式平台桩腿强度对弦管间距敏感性分析

朱亚洲1，孙承猛2，张晓宇2，戚欣2，秦洪德1，姜滨1

（1.哈尔滨工程大学船舶工程学院；2.中国石油集团渤海装备辽河重工有限公司）

以自升式平台桁架式桩腿结构形式优化为目标，进行了桩腿强度对弦管间距敏感性分析，给出了桩腿弦管间距优选值。分析平台所受环境载荷，通过风洞实验获取风暴条件下风载荷数据，通过理论计算得到波浪载荷和海流载荷数据。通过特征值分析得到平台自振周期和一阶偏移值，进而获取计及水动力放大效应的惯性载荷和计及几何非线性效应的惯性矩，分析发现：波流角一定的情况下，计及水动力放大效应的惯性载荷对弦管间距较敏感，随着弦管间距增大基本呈递减趋势；随着弦管间距增大，计及几何非线性效应的惯性矩减小。结合环境载荷计算结果，对不同弦管间距下的桩腿各结构进行了强度校核，对比了各结构强度对弦管间距的敏感性，在此基础上给出了所研究的3种作业水深平台的桩腿弦管间距优选值。图11表4参21

自升式平台；环境载荷；桩腿强度；弦管间距

0 引言

自升式平台因其作业稳定、造价低等优势成为目前浅海油气开发的主流装备。自升式平台主要通过桩腿结构支撑于海底实现主船体升降作业，因此，桩腿结构是自升式平台设计和建造过程中的核心部件。国内外学者针对桩腿结构设计和建造技术展开了深入研究，形成了较为成熟的桩腿结构形式[1-5]。对于作业水深91.5 m（300 ft）以上的自升式平台，桩腿主要为逆“K”斜撑型，以满足海洋环境条件。随着作业水深的不断增加，作业水深107.0～152.4 m（350～500 ft）的平台系列日益成为主流，作业水深以15.24 m（50 ft）步长递增的传统平台划分模式被打破，需要具有个性化功能和作业水深划分更细化的平台类型。

本文针对作业水深91.5 m（300 ft）以上的自升式平台，对影响桩腿承载能力和结构强度的弦管间距进行研究，采用SESAM软件开展桩腿强度对弦管间距敏感性分析，给出该型平台最优弦管间距设计方案，为个性化平台的设计提供参考。

1 环境载荷

在自升式平台设计中，海洋环境条件可以分为静态环境条件和动态环境条件。静态环境条件包括水深、海底地质、气温、水温、湿度和海洋生物等；动态环境条件包括风、波浪和海流。对于自升式平台桩腿强度评估，只需考虑风载荷、海流载荷和波浪载荷的影响。

1.1 风载荷

风载荷是影响自升式平台站立稳定性、结构强度及漂浮稳定性的主控载荷之一，风载荷作用在自升式平台水面以上的部分结构和设备，其大小与风速、受风面积以及结构物或设备高度和形状等因素有关。目前，风载荷计算主要有4种方法：现场实测法、风洞试验法、数值计算法和经验公式法[6-11]。

现场实测法是确定风载荷大小最直接最真实的方法，但该方法费时、费力、成本高，且不能对将来由于平台周围环境变化而可能出现的情况进行研究，因此该方法具有一定的局限性；应用CFD（Computational Fluid Dynamics，计算流体动力学）技术可以计算作用在平台上的风载荷的大小和分布，但该技术在海洋工程结构物风载荷模拟中应用并不多见，主要应用于建筑和飞机工业中[12-13]；经验公式法是计算风载荷的较为简单和快捷的方法，但因其对构件间遮蔽效应等因素考虑不足，计算结果偏于保守；在缺乏母型船资料的情况下，风洞试验是研究风对结构物作用的一种常用方法，该方法可以综合考虑构件形状、高度、位置和遮蔽效应等影响因素。

本文在某国家重点实验室模拟中国A类地表自然流场的TJ-2风洞中按1∶100缩尺比模型（见图1）进行五分量测力实验，对目标平台在风暴条件下的风载荷进行测量，测试时参考高度10 m处风速为51.5 m/s的研究结果，每隔15°为偏角方位，模型在水平面内360°旋转。

图1 风洞实验模型

1.2 波浪载荷

波浪对海水中的结构物可能造成严重伤害，是引起结构物破坏的又一主控载荷。根据研究对象的不同，结构设计分析中所采用的确定波浪模型的方法包括设计波方法和波浪谱统计方法[14-16]。本文建立设计波方法的波浪模型，结合准静态响应分析方法对自升式平台桩腿强度进行评估，为了分析风暴自存工况下的桩腿强度，选用Stokes五阶波以便更好地描述波浪特性。

自升式平台桩腿属于桁架式结构物，其弦管和撑管的截面直径和波长之比满足细长构件要求，因此波浪载荷的计算可以采用Morison公式[17]：

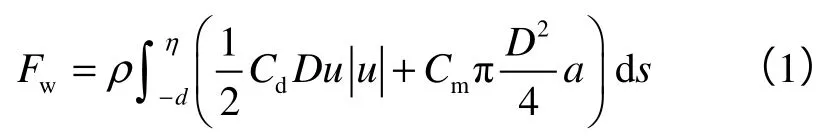
（1）式中的水质点运动速度为水质点与结构响应之间的相对速度，加速度为水质点与结构响应之间的相对加速度。

本文基于Stokes五阶波浪理论，得到任意位置处水质点的速度和加速度，采用SESAM软件WAJAC模块计算得到波浪载荷数值。

1.3 海流载荷

海流的流速随水深而变化，随时间和空间而变化，在船舶与海洋工程结构物计算中，一般不考虑海流引起的涡激振动，将海流视为定常流，即只需要确定海流在海水表面的流速和流速剖面即可[18-19]。

海流和波浪同时存在的情况下，可以将海流速度与波浪水质点运动速度相加，通过（1）式计算出在波浪和海流共同作用下桩腿上的水动力载荷。

海流单独作用在桩腿构件上产生的拖曳力应按下式计算：

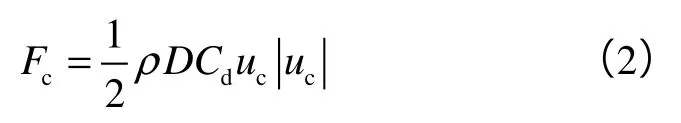
1.4 水动力放大效应

波浪或波浪和海流联合周期性作用将诱发自升式平台结构振动，对随之发生的动力响应必须予以足够的重视。对于海洋工程结构物振动问题，主要涉及结构动力分析方法，迄今为止大体可分为动态系数放大法、频域分析法和时域分析法[20-21]。

本文采用动态系数放大法，以惯性载荷代表动态响应的贡献。动力响应通过全局准静态响应来考虑，将惯性载荷以均匀分布的形式加载或以等效点载荷的形式加载于船体重心。惯性载荷通过单自由度方法（SDOF）求解，该方法假设自升式平台及其基础相当于质量-弹簧-阻尼系统，平台的动态响应幅值与准静态响应幅值的比值是稳定状态下频率和周期的函数，通过DAF（动态放大因子）来计算周期性的正弦激励[17]：

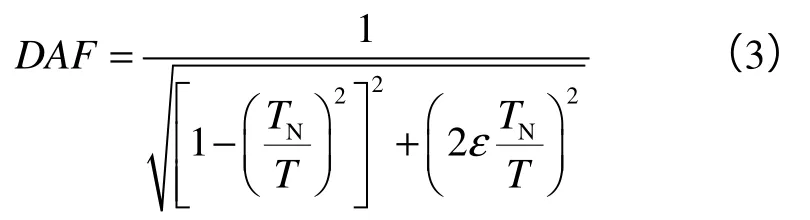
当DAF大于等于1.05时，需要计及惯性载荷影响，

惯性载荷计算公式为：

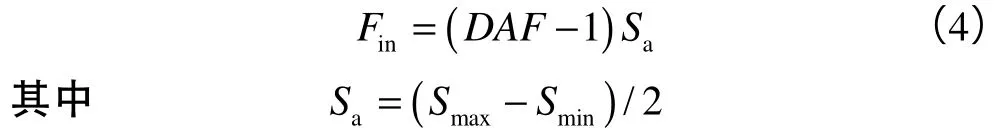
动态放大因子计算过程中的关键是求解平台固有周期TN。本文采用SESAM软件GeniE模块对不同弦管间距的平台模型进行模态分析，得到不同桩腿构型下的固有周期值。

1.5 几何非线性效应

自升式平台在升船状态下，桩腿插入海底，全部载荷由桩腿传递至海底地基土层。与主船体结构相比，自升式平台的桩腿为柔性构件，尤其在水深增加时柔性更加显著，刚度较小，在上述载荷的作用下将产生较大的水平位移，桩靴垂向支反力的作用线不再通过桩腿的型心，导致桩腿弯矩与线性分析结果相比偏大，产生附加变形，属于大位移非线性问题。对此非线性问题，目前主要用附加弯矩法、放大系数法和几何非线性有限元法进行求解[21]。

本文所采用的SESAM软件GeniE模块是基于线弹性理论进行的结构分析，通过多次迭代计算考虑几何非线性效应，计算公式为[17]：

等效惯性矩计算公式为：

等效二次力的计算公式为：

2 有限元计算

2.1 工况条件

选取对桩腿结构设计最不利的风暴条件为分析工况（见表1），取3个作业水深及其对应的气隙和波高条件进行组合，假设浪向和风向一致，波流角（风向角）分别为0°、60°、90°、120°和180°。分别计算了波浪和海流引起的水动力载荷、风载荷、计及DAF效应（水动力放大效应）的惯性载荷和计及几何非线性效应的惯性矩。本文中的风载荷数据（见表2）来源于风洞实验。

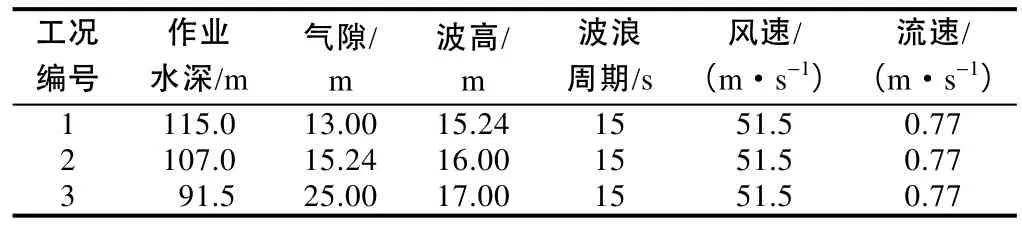
表1 各工况环境参数

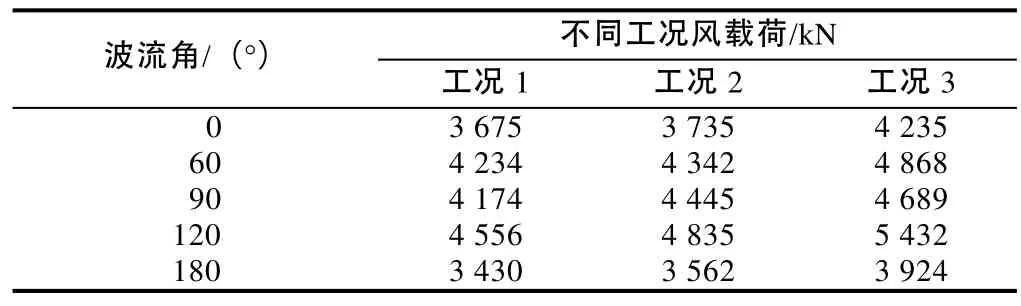
表2 风暴环境下风载荷数据

2.2 模型建立

本文采用SESAM软件GeniE模块建立自升式平台有限元模型，对主船体结构纵横舱壁采用等效截面梁的形式进行模拟，通过调整材料密度和施加质量球的形式来调整整个主船体的质量和重心。利用强度等效原则，桩腿弦管采用等效梁建模。撑管单元以实际尺寸的梁单元进行模拟。

桩腿底部边界条件依据规范取为泥线下3.05 m处铰支[17]。以桩腿弦管、围阱区上下导块和锁紧结构的三点连接模拟桩腿与主船体的连接，上下导块只约束水平位移，锁紧位置同时约束水平和垂直位移。

以107.0 m（350 ft）作业水深的自升式平台为研究对象，型长68.15 m，型宽66.10 m，型深8.30 m，悬臂梁最大外伸21.4 m，桩腿长度155.57 m，平台重心距外底板基线垂直高度10.779 m，空船质量12 564 t。本文采用参数化建模方法对不同弦管间距条件下桩腿在风暴环境中的承载能力进行评估，给出平台最优桩腿弦管间距设计方案。弦管间距10.80 m、11.25 m、11.80 m、12.25 m和12.70 m对应的桩腿质量分别为2 720 t、2 750 t、2 790 t、2 830 t和2 860 t。图2为桩腿结构有限元校核位置。

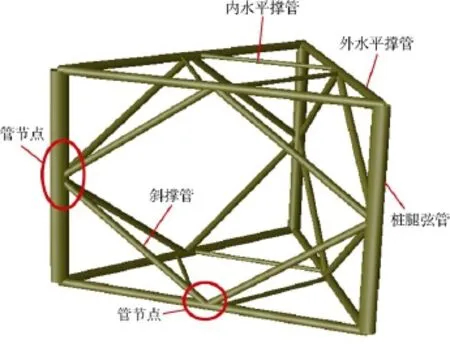
图2 桩腿校核位置示意图

3 计算结果与讨论

通过软件分析，提取了影响惯性载荷的平台固有周期值（见表3）和影响惯性矩的平台水平位移量（见表4）。

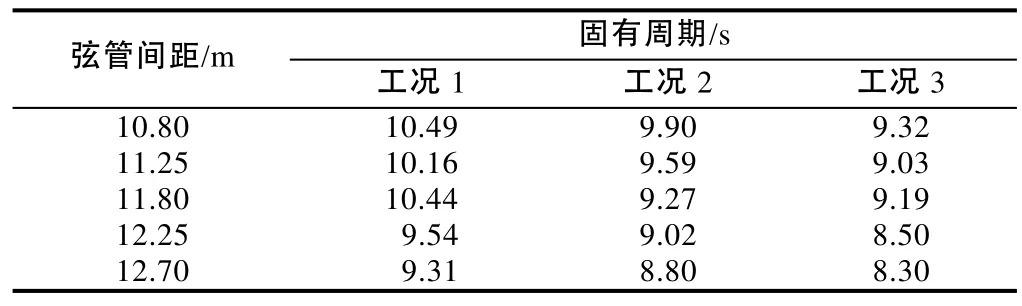
表3 不同弦管间距对应的平台固有周期

3.1 环境载荷计算结果

由图3—图5可知：①波流角一定的情况下，计及DAF效应的惯性载荷对桩腿弦管间距较敏感，工况1条件下，弦管间距10.80 m与弦管间距12.70 m时的惯性载荷相比增加达50%左右。但惯性载荷随波流角变化不明显，可以忽略不计。②计及DAF效应的惯性载荷随弦管间距变大基本呈递减趋势，但在工况1和工况3条件下，弦管间距11.80 m时的惯性载荷大于弦管间距11.25 m时的惯性载荷。这是由于在工况1和工况3条件下，弦管间距11.80 m时的平台固有周期比弦管间距11.25 m时的平台固有周期更接近于波浪周期（见表3），导致DAF值偏大，从而出现惯性载荷逆变现象。

表4 不同弦管间距对应的平台水平位移

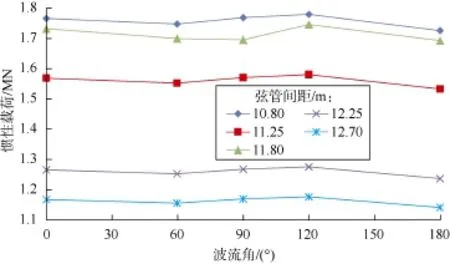
图3 工况1计及DAF效应的惯性载荷

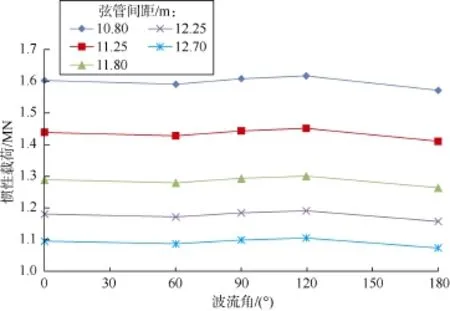
图4 工况2计及DAF效应的惯性载荷

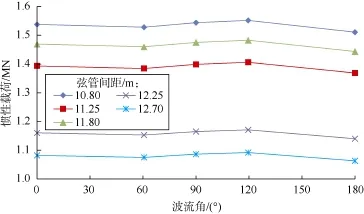
图5 工况3计及DAF效应的惯性载荷

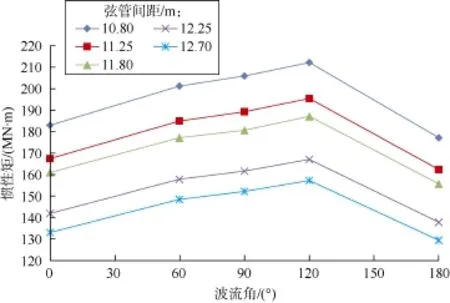
图6 工况1计及几何非线性效应的惯性矩

由图6—图8可知：随着弦管间距增大，平台整体刚度增强，平台水平位移变小，所以计及几何非线性效应的惯性矩随弦管间距增大而减小，总体变化趋势均匀。此外，由表4可知，波流角为120°时，平台水平位移最大，几何非线性效应显著，即在此波流方向作业危险系数最高。

3.2 桩腿强度计算结果

对3种工况下的桩腿结构屈曲和屈服联合校核结

果进行分析，即对UC值（结构屈曲和屈服强度联合计算结果与许用应力的比值）进行分析。

由图9—图11可知：弦管是桩腿所有部件中主要的承力单元，其UC值随弦管间距增大呈缓慢递减趋势；弦管间距12.70 m时的管节点UC值与弦管间距12.25 m时的管节点UC值相比大幅减小，即弦管间距较大时管节点处结构安全性更高；撑管结构中，斜撑管承力较大，其UC值随弦管间距增大呈缓慢递增趋势；外水平撑管UC值为0.1～0.2，内水平撑管UC值为0.2～0.3，安全裕度非常大，因此内、外水平撑管屈曲和屈服联合校核结果对弦管间距的敏感性可不予考虑。

通过上述环境载荷和桩腿强度计算结果分析，结合桩腿质量统计，为了保证弦管的安全裕度，认为弦管间距10.80 m的桩腿形式可满足结构安全要求，同时钢材用量最低，经济性最优。此外，工况2条件下，当弦管间距由11.25 m降至10.80 m时，管节点UC值由0.53突增至0.77，如继续降低弦管间距，管节点处安全性能降低，综合考虑疲劳等因素影响，管节点将率先失效。因此，可以确定10.80 m为最优桩腿弦管间距。

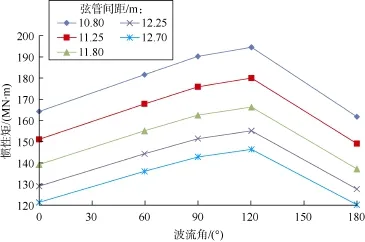
图7 工况2计及几何非线性效应的惯性矩

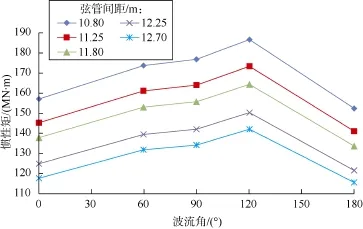
图8 工况3计及几何非线性效应的惯性矩

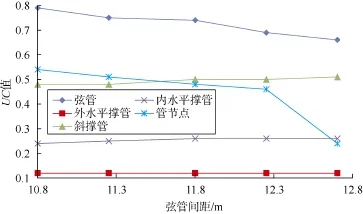
图9 工况1条件下UC值

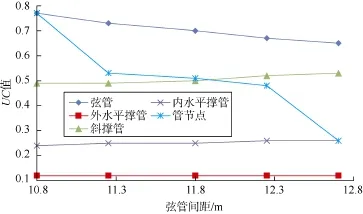
图10 工况2条件下UC值

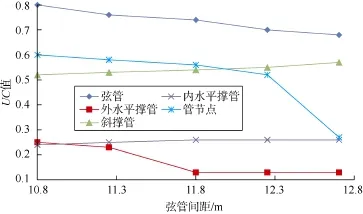
图11 工况3条件下UC值

4 结论

考虑风载荷、海流载荷和波浪载荷，结合有限元计算，给出了计及DAF效应和桩腿几何非线性效应的载荷数据。波流角一定的情况下，计及DAF效应的惯性载荷对桩腿弦管间距较敏感，随着弦管间距变大基本呈递减趋势；随着弦管间距增大，平台水平位移变小，计及几何非线性效应的惯性矩减小。对不同弦管间距的桩腿结构强度进行了对比分析，包括弦管、外水平撑管、内水平撑管、斜撑管和重要管节点等。给出了本文所研究的3种作业水深工况下桩腿弦管间距优选值。

符号注释：

a——水质点运动加速度，m/s2；Cd——水质点拖曳力系数；Cm——水质点惯性力系数；d——水深，m；D——结构特征直径，m；DAF——水动力放大因子；F——等效二次力，N；Fc——海流载荷，N；Fin——惯性载荷，N；Fw——波浪载荷，N；H——作用力至泥面的垂直高度，m；M——等效弯矩，N·m；P——单桩腿轴向载荷，N；PE——单桩腿欧拉屈曲载荷，N；s——深度，m；Sa——1个波浪周期内准静态基础剪力的幅值，N；Smax——最大基础剪力，N；Smin——最小基础剪力，N；T——波浪周期，s；TN——平台固有周期，s；u——水质点运动速度，m/s；uc——海流速度，m/s；δs——主船体线弹性一阶位移，m；Δ——考虑几何非线性效应的近似平台水平位移，m；ε——自升式平台阻尼比，取0.07；η——瞬时波面高度，m；ρ——流体密度，kg/m3。

[1] 任宪刚.深浅海自升式平台结构非线性分析方法研究[D].哈尔滨:哈尔滨工程大学,2012.Ren Xiangang.Research on non-linear analysis method of jack-up unit structure in deeper sea[D].Harbin:Harbin Engineering University,2012.

[2] Cassidy M J.Non-linear analysis of jack-up structures subjected to random waves[D].Oxford:University of Oxford,1999.

[3] 刘秀全,陈国明,畅元江,等.台风条件下深水钻井隔水管触底事故分析及对策[J].石油勘探与开发,2013,40(6):738-742.Liu Xiuquan,Chen Guoming,Chang Yuanjiang,et al.Analyses and countermeasures of deepwater drilling riser grounding accidents under typhoon conditions[J].Petroleum Exploration and Development,2013,40(6):738-742.

[4] Zhang Jian,Tang Wenxian,Su Shijie,et al.Effect of environmental loads on dynamical researches of jack-up[J].Shipping of China,2013,54(1):93-100.

[5] Lu Haohua.The dynamic response of offshore jack-up platform[D].Wuhan:Wuhan University of Technology,2005.

[6] 谭美,冯军,熊飞.自升式钻井平台风载荷研究[J].船舶与海洋工程,2014(1):18-23.Tan Mei,Feng Jun,Xiong Fei.Research on the wind load of jack-up drilling platform[J].Naval Architecture and Ocean Engineering,2014(1):18-23.

[7] 林一,胡安康,熊飞.自升式平台风载荷数值模拟与试验研究[J].水动力学研究与进展,2012,27(2):208-215.Lin Yi,Hu Ankang,Xiong Fei.Numerical simulation and experiment study on wind load of jack-up platform[J].Chinese Journal of Hydrodynamics,2012,27(2):208-215.

[8] 朱航,马哲,谢彬,等.梯度风作用下HYSY-981半潜式平台风载荷与表面风压分布研究[J].中国海上油气,2010,22(4):270-274.Zhu Hang,Ma Zhe,Xie Bin,et al.Wind loads and wind pressure distribution acting on HYSY-981 semi-submersible platform in gradient wind field[J].China Offshore Oil and Gas,2010,22(4):270-274.

[9] 毛东风,段梦兰,李新仲,等.基于灰色关联的深水浮式油气开发平台选择[J].石油勘探与开发,2013,40(6):743-746.Mao Dongfeng,Duan Menglan,Li Xinzhong,et al.Selection of deepwater floating oil platform based on grey correlation[J].Petroleum Exploration and Development,2013,40(6):743-746.

[10] 林一,胡安康,孙建.自升式平台风载荷的空气动力学干扰研究[J].船舶与海洋工程,2013(2):5-10.Lin Yi,Hu Ankang,Sun Jian.Research on wind load aerodynamic interference of jack-up platform[J].Naval Architecture and Ocean Engineering,2013(2):5-10.

[11] 林长刚.自升式海洋平台风载荷及风暴环境图谱研究[D].大连:大连理工大学,2013.Lin Changgang.Research on wind loads and environmental charts for storm of jack-up platform[D].Dalian:Dalian University of Technology,2013.

[12] 王福军.计算流体动力学分析:CFD 软件原理与应用[M].北京:清华大学出版社,2004.Wang Fujun.Computational fluid dynamic analysis:CFD principle and application[M].Beijing:Tsinghua University Press,2004.

[13] 王瑞金,张凯,王刚.Fluent技术基础与应用实例[M].北京:清华大学出版社,2008.Wang Ruijin,Zhang Kai,Wang Gang.Technology base and application examples of Fluent[M].Beijing:Tsinghua University Press,2008.

[14] 黄鲁蒙,张彦廷,张磊,等.半主动式钻井绞车升沉补偿系统[J].石油勘探与开发,2013,40(5):620-624.Huang Lumeng,Zhang Yanting,Zhang Lei,et al.Semi-active drilling drawworks heave compensation system[J].Petroleum Exploration and Development,2013,40(5):620-624.

[15] 钱昆.浮体在大幅波浪中的运动和荷载计算研究[D].大连:大连理工大学,2004.Qian Kun.Study on calculation of motions and loads on floating body in large amplitude waves[D].Dalian:Dalian University of Technology,2004.

[16] 郭兴乾.深水钻井船波浪载荷预报[J].船舶,2012,23(3):40-44,67.Guo Xingqian.Wave loading prediction of deep water drilling ship[J].Ship &Boat,2012,23(3):40-44,67.

[17] Society of Naval Architects and Marine Engineers.SNAME Technical and research bulletin 5-5A site specific assessment of jack-up units[S].New Jersey:Society of Naval Architects and Marine Engineers,2012.

[18] 高畅.自升式平台桁架腿波流载荷分析与实验研究[D].天津:天津大学,2010.Gao Chang.Analysis and experimental study of wave-current loads on jack-up truss-type leg[D].Tianjin:Tianjin University,2010.

[19] American Bureau of Shipping.ABS rules for building and classing mobile offshore drilling units[S].New York:American Bureau of Shipping,2014.

[20] 吴小平,陆晟.自升式钻井平台环境载荷及结构强度[J].上海造船,2010(3):36-41.Wu Xiaoping,Lu Sheng.Environmental loading and structure strength of self-elevating drilling unit[J].Shanghai Shipbuilding,2010(3):36-41.

[21] DET NORSKE VERITAS.Recommended practice DNV-RP-C205:environmental conditions and environmental loads[S].Oslo:DET NORSKE VERITAS,2012.

（编辑 胡苇玮）

Sensitivity of self-elevating unit leg strength to different chord space

Zhu Yazhou1,Sun Chengmeng2,Zhang Xiaoyu2,Qi Xin2,Qin Hongde1,Jiang Bin1
(1.College of Shipbuilding Engineering,Harbin Engineering University,Harbin 150001,China;2.China Petroleum Liaohe Equipment Company,CNPC,Panjing 124010,China)

Aiming to optimize the truss leg structure of self-elevating unit,the sensitivity of leg strength to different chord space was analyzed,and the optimal value of chord space for legs was presented.The wind load under storm condition was obtained by wind tunnel test,and the wave and current loads were calculated based on theoretical and numerical methods.The natural vibration period and first order offset value were obtained by eigenvalue analysis,thus the inertial load considering the dynamic amplification factor and the inertial moment considering the geometric nonlinearity were obtained.It is found out through analysis that:the inertial load considering the dynamic amplification factor is more sensitive to chord space under a certain wave and current angle,and decreases with the increase of chord space in general;the inertial moment considering the geometric nonlinearity also decreases with the increase of chord space.According to the environment load,the strength of leg structures at different chord spaces were checked and the sensitivity of the structure strength to chord space was compared.Based on this,the optimal values of chord space for legs at three water depths were presented.

self-elevating unit;environment load;leg strength;chord space

中国石油装备制造分公司科技统筹项目“CP-375自升式钻井平台设计及关键部件研制”（Y-14M000003）

TE53

A

1000-0747(2015)05-0656-06

10.11698/PED.2015.05.14

朱亚洲（1982-），男，江苏盐城人，哈尔滨工程大学船舶工程学院在读博士研究生，主要从事船舶与海洋工程性能分析与结构安全性评估方面的研究工作。地址：辽宁省盘锦市兴隆台区迎宾路32号，邮政编码：124010。E-mail:zhuyazhou_cplec@126.com

2015-01-27

2015-07-13