聚晶金刚石钻头切削齿切削岩块过程的有限元模拟

Pryhorovska T O，Chaplinskiy S S，Kudriavtsev I O

（Ivano-Frankivsk National Technical University of Oil and Gas,Ukraine）

聚晶金刚石钻头切削齿切削岩块过程的有限元模拟

Pryhorovska T O，Chaplinskiy S S，Kudriavtsev I O

（Ivano-Frankivsk National Technical University of Oil and Gas,Ukraine）

建立了聚晶金刚石（PDC）钻头切削齿切削岩石过程的有限元模型，模拟了不同形状切削齿不同切削深度下的线性和圆弧切削过程。模拟前确定了切削齿的空间形态、切削速度、切削深度、材料的流变模型、摩擦模型等。模拟结果表明：线性和圆弧切削过程没有本质区别；各类切削齿的切削力波动均为振荡和不均匀的，不存在周期性；采用同一切削齿时不同切削深度下的切削力波动没有类似规律，但切削深度增加会引起波动幅度增大；切削深度为0.5 mm和1.0 mm时，切削参数保持稳定后平均切削力减小，而切削深度为2.0 mm时，进入稳定切削区后平均切削力并未减小；使用球形齿和圆锥形齿时切削力较小，而使用锥形齿、斜角形齿和平板形齿时切削力较大；采用平板形齿时切削力波动图上单位时间内峰数最少，采用球形齿时最多。图5表1参13

PDC钻头；切削齿；切削过程；切削力；有限元模拟

0 引言

近年来，因其简单高效的特点，有限元法在包括岩石切削在内的切削工艺模拟方面得到了广泛应用[1-2]。该方法可用于模拟材料非均质性、非线性和边界条件对切削过程的影响。例如，它可以用于塑性变形数学建模、切削片（切削刃）应力应变状态评价、切削工具结构元件及工作条件的优化、残余应力预测和切削力动态分析等。

Ansys Explicit软件可利用有限元法进行钻井工具（包括PDC钻头）的优化设计，该方法对于高成本的钻头、钻头部件和钻头实验尤其重要。但在实际应用时无法建立满足如下2个要求的有限元网格：①样本的局部误差在有限元网格上均匀分布；②全局误差满足预先设定的精度准则。因而，Ansys Explicit软件并不能保证所获得的数值解的适用性和准确性。

PDC钻头的性能可用切削力的稳定性进行表征，切削力不稳定会引起钻头的涡动现象。因此，有必要对PDC钻头及钻头部件（切削齿、刀翼）进行优化设计以保证切削力稳定。PDC钻头的研究趋势是确保每个元件乃至整个钻头的稳定。

对切削齿形状的研究大多针对切削齿磨损和破岩效率[3-7]。尽管开发和应用了椭圆形、圆锥形、镶嵌状的切削齿，但PDC钻头切削齿的常用形状是圆柱形[4-5]。此外，未见关于切削齿形状对切削力波动影响的文献报道，有必要开展相关实验和模拟。前人在研

究中考虑了岩屑、新形成的岩石表面和切削齿之间的动态相互作用，并形成了三维有限元建模的框架，以正确模拟在室内岩石切削实验中观察到的岩石破碎过程，结果表明实验数据和模拟结果吻合良好[3-5]。因此，在缺乏实验数据的情况下，可以通过有限元模拟对整个切削过程进行定性表征，并获取岩体应力和岩石反作用力的波动情况。对于单个切削齿或整个钻头的切削力的波动，尚缺乏明确的理论。岩石非均质性对切削力波动的影响研究较多，但缺乏对该影响的定量表征，只有间接认知方法[8-9]。

因此，本文采用有限元法模拟不同形状PDC钻头切削齿的线性和圆弧切削过程，研究切削齿形状对切削力波动的影响，以确定切削力波动最小的切削齿形状，从而在设计刀翼和钻头时尽可能地减小切削力的波动。

1 有限元模型

切削力模拟的原始数据包括：切削齿的空间形态、切削参数（切削速度、切削深度）、材料的流变模型和摩擦模型。

所建模型基于刚体定点运动的基本公式[10]：

边界条件包括：刚体边界上的受力、刚体边界线的位移及接触区边界上的受力，用如下表达式表示：

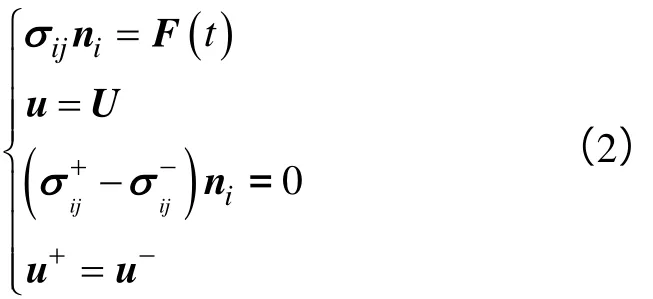
质量守恒方程为：

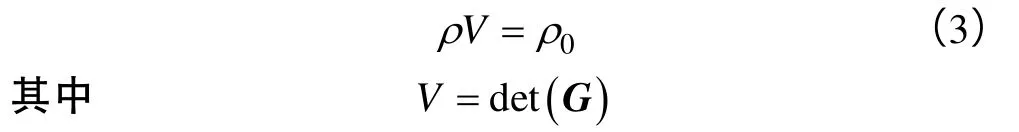
能量方程为：

受力平衡方程为：

初始时刻模拟刚体所有点的状态为：

根据（1）式、（5）式，加速度矢量可以表达为：

速度矢量和位移矢量通过中心差分法进行定义：

为确定运动引起的内力，计算出应变率张量：

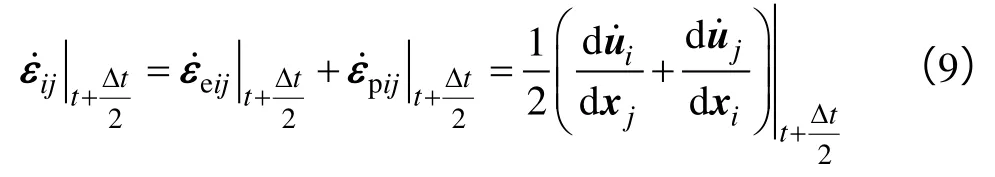
根据文献[4]，又有：

破岩区内岩石应变率大，在常用切削速度条件下，可假设为绝热变形。因此，变形区域中的温度为：

有限元模型节点上的应力计算公式为：

对于内部节点：

本文根据广义胡克定律提出了弹性变形的流变模型，用于计算钻井工具和岩层所受的应力，岩块也呈塑性变形。采用Johnson-Cook方程[9]计算损伤应力：

接触问题和接触边界力的问题用罚函数法解决[4,11]。用以下模型计算接触剪切应力：

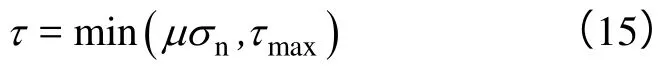
然后利用应力与破坏准则检查岩块每个有限元网格可能出现的失效现象。本文选用Johnson-Cook累积塑性变形准则[9]作为塑性材料的破坏准则。每步积分对当前时间t递加Dt，再重复上述计算步骤。最大积分步长由下式确定：

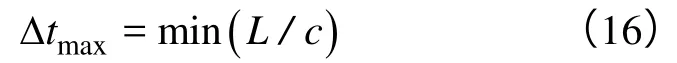
该方法的特点是可对问题进行动态描述，可获得切削齿在任意工作时间点的定性模拟数据。

PDC钻头切削齿过热的问题非常严重。接触区的热应力最大，影响整体应力的分布，但切削区温度和压力对切削过程的影响可以忽略，原因在于过热问题与切削齿的材料及切削齿的磨损有关，切削齿材料不

同，则接触区的热应力分布也不同。因此，分析切削力和应力波动时应该关注切削齿材料。

由于切削是一个复杂的过程，目前还无法用解析解描述。因此，本文数值模拟研究采用以下假设：忽略切削区的加热效应；摩擦系数沿切削齿的整个长度方向为恒定值，不受切向应力影响；切削刃无磨损，不考虑切削齿的磨损。

2 岩层切削数值模拟

模拟的目的是在考虑切削深度和接触区加热的情况下找出切削力波动最小的切削齿形状。

采用线性四边形有限元网格进行建模[4]。为了最大限度地提高计算速度，切削齿和岩块的有限元网格均为均匀网格，切削刃区域的有限元网格尺寸减小。图1为线性和圆弧切削方案示意图。

边界条件为：圆弧和线性切削的岩块均为三轴固定；对于线性切削，切削齿的线速度恒定，对于圆弧切削，切削齿垂直线速度和水平面上圆周速度均恒定不变。初始条件为：整个切削齿和岩块的温度和压力恒定，切削速度为零，所有节点均无负载。

根据切削齿制造商的网站给出的PDC钻头切削齿确定了模拟采用的切削齿类型（见图2）[12]。切削齿尺寸为：高度18 mm，直径13 mm。

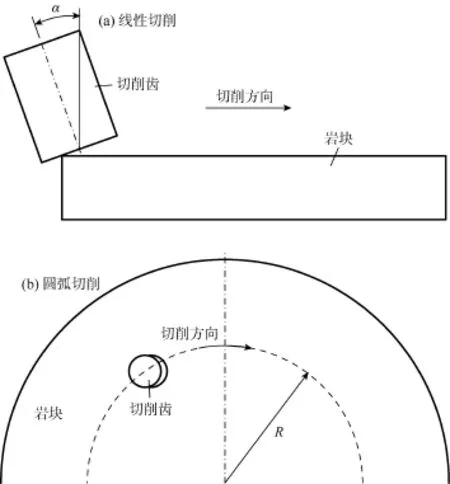
图1 线性和圆弧切削方案

图2 模拟选用的切削齿类型

针对模拟的切削齿和岩块，选择Ansys Explicit软件模拟时采用的材料，分别为BoronCarbi和Concrele L，二者的特性如表1所示。

切削参数为：①线性切削。切削深度0.5 mm、1.0 mm和2.0 mm，切削速度0.5 m/s，切削时间0.15 s，切削角20°。②圆弧切削。圆周速度0.5 m/s，垂直速度1 mm/s和2 mm/s，切削角20°，切削时间0.15 s，切削半径35 mm。所选定的切削参数与实际钻井作业数据和实验数据相符。在确定切削参数时，为了分析切削深度对切削力波动的影响，模拟了不同的切削深度。

表1 模拟使用的材料特性

3 数值模拟结果

图3、图4分别为线性和圆弧切削的模拟结果之

一。图5为采用第1类切削齿（平板形）线性切削的切削力波动图。

由模拟结果可以得出以下结论。

①切削齿附近的狭窄区域内存在一个剪切区域。可以观察到切削面下塑性变形的扩展以及岩块之间的间隙。在切削过程中，可观察到由有限元组成的切削单元的分离以及岩层位移的增加。这与现场实际和已发表文献中的实验数据[2,13]相符。

②应力最大值分布在切削区域，与典型的岩石切削的应力分布预测结果[2,13]相符。剪切应力随机分布。

图3 线性切削模拟结果

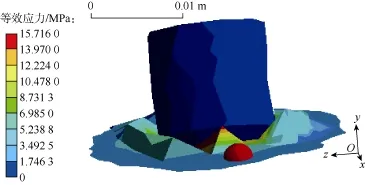
图4 圆弧切削模拟结果

图5 典型的切削力波动图（第1类切削齿，线性切削）

③无论是线性还是圆弧切削，所有类型切削齿的切削力波动均为振荡和不均匀的，切削力随机变化，不具有周期性波动特征。对于一定类型的切削齿，不同切削深度下的切削力波动也没有类似规律。

④虽然切削力大小和切削深度关系不明显，但切削深度增加会引起切削力波动幅度增大。切削齿向岩块施加力时切削力波动最强烈，这是由于切削齿与岩石接触时伴随着冲击。

⑤对于线性切削：切削深度为0.5 mm和1.0 mm时，切削齿切入岩块过程中切削力不断增大，到达稳定切削区后平均切削力减小，并存在少数的切削力“跳跃”；切削深度为2 mm时，切削齿切入岩块过程中切削力不断增大，但切削参数保持稳定后平均切削力并未减小，切削的施加区和稳定区之间没有明显的界限。稳定切削区的特点是存在大量的切削力峰值。3种切削深度下，球形切削齿和圆锥形切削齿切削力较小，锥形齿、斜角形齿和平板形齿切削力较大。根据此结果，切削齿的接触面积越大，其切削力越小。然而，由于球形和圆锥形切削齿仅与岩石部分接触，球形和圆锥形切削齿的实际接触面积小于平板形切削齿。因此，切削齿的接触面积与切削力大小间的关系难以确定。切削力波动图上单位时间内的峰数平板形齿最多，球形齿最少。

⑥对于圆弧切削：岩石破坏概貌与线性切削相似。由于切削轨迹曲率没有实质性的影响，观察到的圆弧切削与线性切削结果并无本质区别。

4 结论

本文建立了PDC钻头切削齿切削岩石过程的有限元模型，模拟了不同形状切削齿不同切削深度下的线性和圆弧切削过程。结果表明：两种切削方式的切削过程没有本质区别；各类切削齿的切削力波动均为振荡和不均匀的，切削力的值是随机的；采用同一切削齿时，不同切削深度下的切削力波动没有类似规律；切削深度为0.5 mm和1.0 mm时，切削齿切入岩层过程中切削力不断增大，到达稳定切削区后平均切削力减小，而切削深度为2.0 mm时，切削的施加区和稳定区之间没有明显的界限；球形切削齿和圆锥形切削齿的切削力较小，锥形切削齿、斜角形切削齿和平板形切削齿的切削力较大；切削力波动图上单位时间内的峰数平板形齿最多，球形齿最少。

符号注释：

A，B，C，m，n——Johnson-Cook方程中系数；c——材料内平面声波的速度，m/s；Cv——热容，J/K；D——切削齿直径，mm；——能量变化率，Pa/s；f——作用在有限元网格节点上的合力，Pa；fcontact——作用在有限元网格节点上的接触边界力，Pa；fload——作用在有限元网格节点上的外力，Pa；fv——单位质量的体积力矢量，m/s2；F——刚体边界上的受力，Pa；Fload——初始时刻刚体边界区域受力，Pa；G——位移梯度；H——切削齿高度，mm；I——作用在有限元网格节点上的内力，Pa；L——有限元特征尺寸，m；Mij——质量矩阵，kg；ni——法向量；q——体积黏度，Pa；R——圆弧切削的切削半径，mm；t——时间，s；T——温度，K；T0——初始时刻温度，K；Tm——熔解温度，K；u——刚体点位移矢量，m；u+——刚体点拉伸位移矢量，m；——刚体点压缩位移矢量，m；——刚体点速度矢量，m/s；——刚体点加速度矢量，m/s2；U——初始时刻位移矢量，m；——初始时刻速度矢量，m/s；——初始时刻加速度矢量，m/s2；α——切削角，（°）；——Kronecker符号；Δt——积分时间步长，s；——应变率张量，s-1；——弹性变形速度张量，s-1；——塑性变形速度张量，s-1；——塑性变形大小；——塑性变形速度大小；——初始时刻塑性变形速度大小；η——机械效率，%；μ——摩擦系数；r——给定时间内的材料密度，kg/m3；r0——材料初始密度，kg/m3；σij,j——柯西应力张量的分量，Pa；σn——切削齿接触区的法向应力，Pa；σs——损伤应力，Pa；σ+——拉应力张量，Pa；σ-——压应力张量，Pa；τmax——最大接触应力，Pa。

[1] Ju P,Wang Z,Zhai Y,et al.Numerical simulation study on the optimization design of the crown shape of PDC drill bit[J].Journal of Petroleum Exploration &Production Technology,2013,4(4): 343-350.

[2] Maria J.Numerical modeling of rock cutting and its associated fragmentation process using the finite element method[D].Pittsburgh: University of Pittsburgh,2012.

[3] Appl F C,Wilson C C,Lakshman I.Measurement of forces,temperatures and wear of PDC cutters in rock cutting[J].Wear,1993,169(1): 9-24.

[4] Azar M,White A,Segal S,et al.Pointing towards improved PDC bit performance: Innovative conical shaped polycrystalline diamond element achieves higher ROP and total footage[R].SPE 163521-MS,2013.

[5] Bellin F,Dourfaye A,King W,et al.The current state of PDC bit technology[J].World Oil,2010,231(9): 67-71.

[6] Li X,Zhao F,Summers D.Failure modes of PDC cutters under different loads[J].Transactions of the Nonferrous Metals Society of China (China),2002,12(3): 504-507.

[7] Institute of Superhard Materials.Research and development of new drilling tools design for drilling in special conditions[R].Kiev: Ministry of Geology of Ukraine Soviet Socialistic Republic,1984.

[8] Spanos P D,Chevallier A M,Politis N P.Nonlinear stochastic drill-string vibrations[J].Journal of Vibration and Acoustics,2002,124(4): 512-518.

[9] Fridman E.Bounds on the response of a drilling pipe model[J].IMA Journal of Mathematical Control &Information,2010,1(4): 513-526.

[10] Gao Ke,Li Meng,Dong Bo,et al.Bionic coupling polycrystalline diamond composite bit[J].Petroleum Exploration and Development,2014,41(4): 485-489.

[11] Johnson G R,Cook W H.A constitutive model and data for metals subjected to large strains,high strain rates and high temperatures[C]//Proceedings of the 7th International Symposium on Ballistics.Orlando: International Ballistics Society,1983: 541-547.

[12] Supreme Superabrasives Co.,Ltd.Supreme PDC cutters for oil/gas drilling and mining bits[EB/OL].Zhengzhou: Supreme Superabrasives Co.,Ltd.[2014-09-20].http://www.supremesuperabrasives.com/ product_en_2.htm.

[13] Zhou Yaneng.Numerical Simulation of rock drilling with finite elements[D].Pittsburgh: University of Pittsburgh,2013.

（编辑 胡苇玮）

Finite element modelling of rock mass cutting by cutters for PDC drill bits

Pryhorovska T O,Chaplinskiy S S,Kudriavtsev I O
(Ivano-Frankivsk National Technical University of Oil and Gas,Ivano-Frankivsk 76000,Ukraine)

A finite element model of the process of polycrystalline diamond compact (PDC) drill bit cutters cutting rocks was built,and the rock linear and circular cutting processes for different shapes of PDC drill bit cutters were simulated.The following initial data was stated before modelling: spatial form of cutter,cutting speed,cutting depth,rheological model of the processed material,and frictional model.Simulation results show that: there is no essential difference between curricular cutting and linear cutting;all the obtained relations of cutting forces were oscillatory and unevenly for all types of cutters;cutting depth increasing causes oscillation amplitude increasing,although no clear relationship between the fluctuations amplitude and the cutting depth is observed for the same cutter;for cutting depth in 0.5 mm and 1.0 mm,the average cutting force decreases when the cutting parameters are stable,while for cutting depth in 2.0 mm,the stable cutting regime is not accompanied by average cutting force decreasing;the cutting forces are smaller for spherical shape cutter and pick-shaped cutter,and bigger for tapered shape cutter and cutters with bevel and flat;the number of peaks per unit time on fluctuation diagram: the minimum value for flat cutter,maximum value for spherical shape cutter.

PDC bit;cutter;cutting;cutting force;finite element method

P634.4

A

1000-0747(2015)06-0812-05

10.11698/PED.2015.06.16

Pryhorovska T O（1979-），男，乌克兰人，硕士，伊万诺-弗兰科夫斯克国立石油天然气技术大学助理教授，主要从事钻头设计、钻柱振动及钻井统计分析等方面的研究工作。地址：Ivano-Frankivsk National Technical University of Oil and Gas,15 Karpatska Street,Ivano-Frankivsk,76000,Ukraine。E-mail：pryhorovska@gmail.com

2014-10-16

2015-10-12