应用多中心分区方法构建H3分子反应势能面

戴 伟 陈柳杨 郑利敏 杨明晖,*

(1湖北第二师范学院物理与机电工程学院, 武汉 430205;2中国科学院武汉物理与数学研究所, 武汉 430071)

应用多中心分区方法构建H3分子反应势能面

戴 伟1,2陈柳杨2郑利敏2杨明晖2,*

(1湖北第二师范学院物理与机电工程学院, 武汉 430205;2中国科学院武汉物理与数学研究所, 武汉 430071)

势能面在分子反应动力学的研究中起着非常重要的作用. 本文提出了一种新的势能面构建方法——多中心分区法. 通过比较London-Eyring-Polanyi-Sato (LEPS)势能、多体展开势能、置换对称不变多项式三种方法, 确定了H3分子的最佳势能函数表达形式, 并应用准经典轨线方法分析了势能面的合理性, 结果表明置换对称不变多项式能很好地描述H3分子的势能面特征. 结合置换对称不变多项式和本文提出的多中心分区方法,可以有效改善H3分子势能面的精度并可能推广到高维反应势能面.

势能面拟合; 准经典轨线法; 多中心分区

1 引 言

随着实验技术的快速发展, 分子反应动力学实验方法1取得了长足进步, 理论研究能够解释并预测基元化学反应的动态结构、反应过程和反应机理,是实验研究的重要补充手段. 势能面是理论研究中的一个重要概念, 它描述反应体系中多个原子间的相互作用, 因此需要构造准确的势能面以尽可能真实表达分子反应的势能面,2通常构造势能面的方法可以分为两类, 一种是插值方法,3–23Collins等3–15在高维插值势能面方面做了很多系统的工作, 还有应用三次样条插值、16,17Shepard 插值、18,19Modified Shepard 插值20–22来构建分子反应势能面的研究工作,通过高维插值构建势能面, 需要较多的从头算数据点. 另一种是函数拟合,23–30Corchado等24通过解析表达式拟合构建了H+CH4势能面, Varandas等25通过双多体展开(DMBE2001)构建了H3势能面, Bowman等26通过选择满足置换对称性的多项式作为势能函数, 构建了置换对称不变多项式(PIP)势能面, 以及最近得到广泛应用的的神经网络方法.27–30选择合适的势能函数形式能够有效地提高势能面精度.

在势能面构建过程中, 基于误差是按区域分布这一特点, 我们认为如果按区域多中心分区拟合,将会有利于改善势能面的精度. 基于这一思想, 本文发展了多中心分区拟合方法并应用到H3分子反应势能面的构建中, 相比高维插值方法, 节约计算资源, 相比传统的函数拟合方法, 提高势能面的精度,该项工作可为研究较大体系的反应动力学提供一个新的思路.

2 H3分子势能面的解析表达式

2.1 训练集的数据来源及要求

本文H3结构与能量的训练集数据由DMBE2001势能面25产生. 其中R1, R2, R3取值区间为0.05–0.5 nm,步长为0.01 nm, 坐标的选取如图1所示. 剔除能量高于40000 cm–1的能量点, 同时剔除不能构成几何形状的数据点.

2.2 势能函数形式的选取

改善势能面拟合精度的关键在于选择合适的势能函数形式. Connor31指出, 理想的势能函数应满足以下条件:

(1) 能准确描述反应物和产物通道的渐进性质;

(2) 能正确显示出体系的对称性;

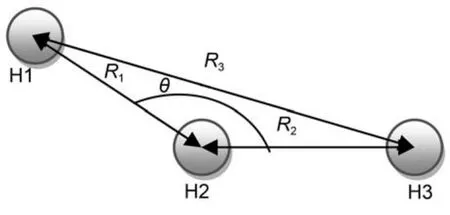
图1 H3体系坐标Fig.1 Coordinates for H3system

(3) 在有实验数据或者(非经验的)理论数据的反应区域能准确描述体系的能量;

(4) 在没有实验数据和理论数据的反应区域能合理描述体系的行为;

(5) 保证各个区域光滑连接;

(6) 势能函数及其微分的代数形式尽可能简单; (7) 尽可能少的数据点就能达到拟合的精度.本文讨论以下三种势能函数在拟合H3反应势能面的精度.

2.2.1 LEPS势能

Eyring和Polanyi32利用London对三原子体系的量子力学势能近似构建了London-Eyring-Polanyi (LEP)势能面, Sato33又在他们的基础上进行了修正,去掉了势垒顶端不合理的势阱, 得到了London-Eyring-Polanyi-Sato (LEPS)势能面. LEPS也适合于多原子分子, 由于形式比较简单, 参数少, 能够反映出体系的主要特征, 在分子动力学发展的早期应用特别广泛. 三原子体系的能量采用London形式表示:

其中, Q为库能积分, J为交换积分,

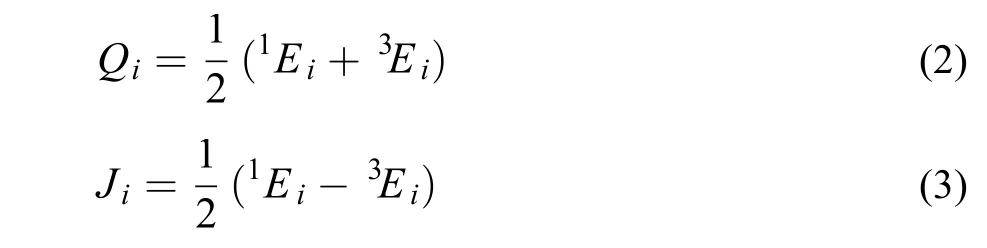
式中1Ei为双原子Morse函数,3Ei为反Morse函数, 表达式如下:

式中Di、和βi分别表示双原子分子基态离解能、平衡核间距和光谱常数, 可通过从头计算确定, Si是针对不同体系引入的可调参数, βi为光谱常数, 可表示为

c为光速, ωe为振动光谱常数, μ为折合质量.

为确定LEPS势能中的可调参数Si, 扫描了一条均方根偏差(RMSD)随Si变化的曲线, 由图2可以看出, Si取0.10时, 均方根偏差最小. 构建的LEPS势能面如图3所示, 势能中所用参数如表1所示.

2.2.2 多体展开势

多体展开法34是构建多原子分子势能面的常见方法之一, 它由单体项、二体项和多体项构成. 表达形式如下:

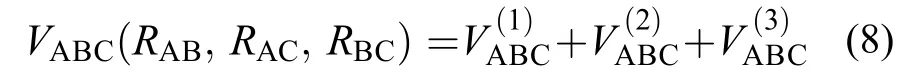
其中,

其中RAB为双原子体系AB的键长, DeAB是离解能, ReAB是平衡核间距, αAB是Morse参数. 同理可得AC、BC双原子系统的Morse势表达式. H3体系的离解能为0.293526 hartree, 平衡核间距为1.390 Bohr, Morse参数为8.10036.

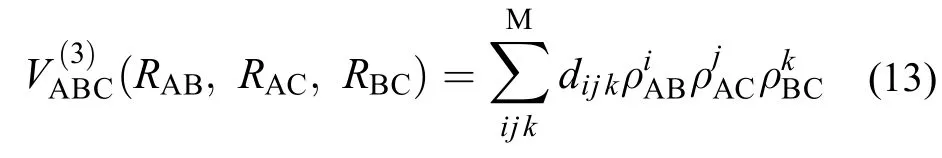
式中的为非线性系数, ρBC和 ρAC的表达式与此类似, d是拟合参数, M是展开的阶数, 本文中M = 5.

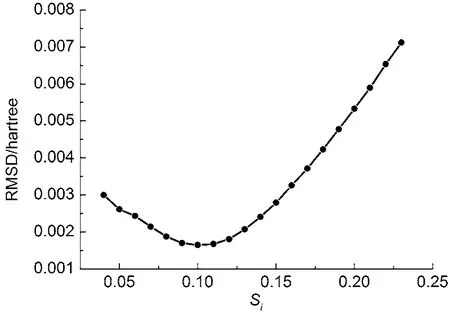
图2 均方根偏差(RMSD)随Si参数的变化关系Fig.2 Relationship between the root mean square deviation (RMSD) and the Siparameter

图3 H3分子30°的势能等值图Fig.3 Contour plots of potential energy surface for H3at 30°

表1 LEPS势能参数数值Table1 Values of LEPS potential parameters

2.2.3 置换对称不变多项式(PIP)方法

美国Emory大学化学系Joel M. Bowman教授在构建多原子分子势能面时, 选择满足置换对称性的多项式作为势能函数, 对势能面精度有很大改善,其拟合表达式27如下:

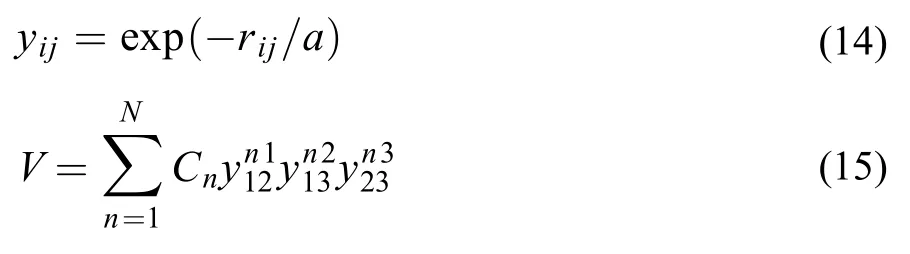
式中a为可调参数, 在本文中取1.8 bohr, n1, n2, n3= 1, 2,, 10且n1+ n2+ n3≤ 18, N为拟合表达式中待定参数总和, 文中取970项.

2.2.4 计算结果

为了进一步研究势能函数带来数值误差的分布状况, 本文统计了三种不同势能函数在不同散射角度下的均方根偏差(见表2). 结果表明: (1) PIP方法能准确描述H3分子势能面的结构特征, 统计误差最小; (2) 所有势能函数在60°散射时, 误差最大, 分析原因可能是DMBE2001势能面25提供的数据集在这一角度本身不能很好描述H3体系的相互作用, 需要通过从头计算做进一步的验证.

图4、图5、图6是三种拟合表达式60°时的势能面等值图, 由图可以看出, 势能面整体趋势区别不大, 第一种拟合表达式近程排斥区域最大, 第二种拟合表达式近程排斥区域最小, 在三体解离区, 也存在一定差别, 其它区域三种形式基本吻合.

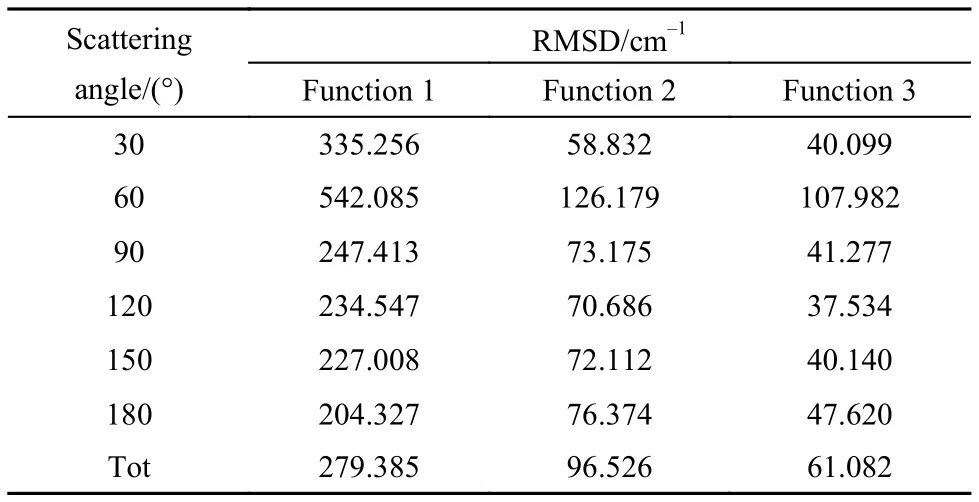
表2 不同散射角下势能面的RMSDTable2 RMSD of potential energy surface under different scattering angles

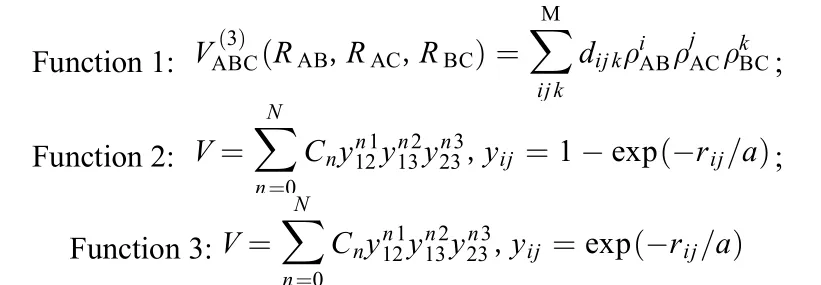
图7是三种拟合势能面及LEPS势能面的准经典轨线计算结果, 总体来说, 与文献提供的势能面在

图4 公式1拟合下60°时的势能面等值图Fig.4 Contour plots of potential energy surface for the Function 1 at 60°

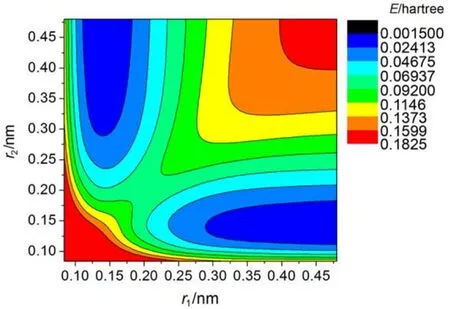
图5 公式2拟合下60°时的势能面等值图Fig.5 Contour plots of potential energy surface for the Function 2 at 60°

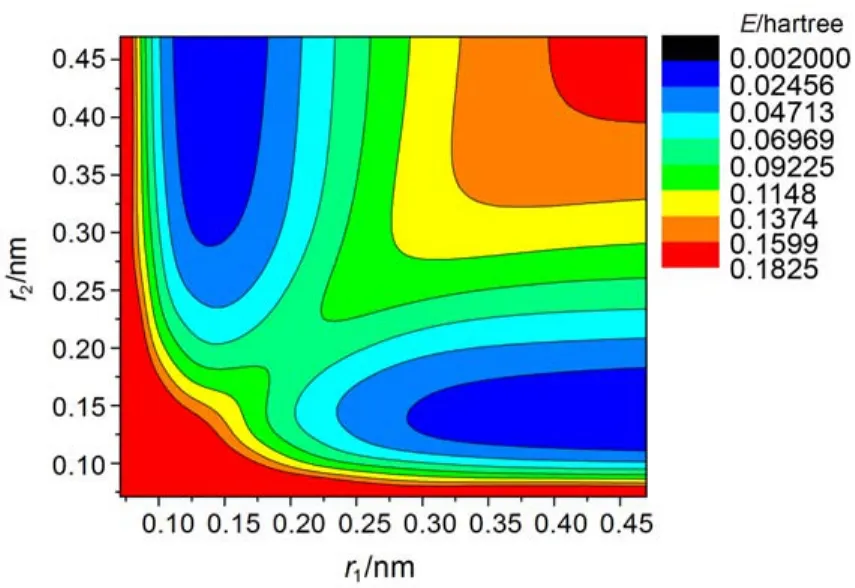
图6 公式3拟合下60°时的势能面等值图Fig.6 Contour plots of potential energy surface for the Function 3 at 60°

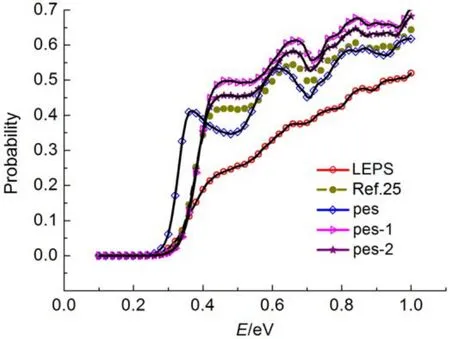
图7 不同势能函数表达式的准经典轨线结果比较Fig.7 Comparison of the quasi-classical trajectory results between different potential energy functions

基本趋势上是一致的, LEPS势能面参数少, 使用方便, 但高能区域偏差较大, 第一种拟合表达势能面在低能区域偏差较大, 不适宜用来描述H3分子相互作用, 第二种和第三种势能面在低能区与文献值符合很好, 高能区域, 第三种势能面符合更好, 综合动力学结果分析, PIP方法能更好地描述H3体系的相互作用.

3 应用多中心分区拟合构建H3分子势能面

3.1 多中心分区拟合的思想由来

图8是本文构建势能面与数据测试集的差分图(散射角60°), 图中表示的是采用PIP方法构建的势能面与测试数据的差值, 用来描述势能面的回归特性. 由图可以看出, 误差呈区域分布, 大部分区域吻合较好, 误差不大, 只有在鞍点区域到三体离解区域过渡时, 两种势能差别较大. 拟合势能面与测试数据集的吻合度按区域分布, 有些地方高于测试值,有些地方低于测试值, 鉴于误差是按区域分布这一特点, 我们预测如果在构建势能面时, 按区域多中心分区拟合, 对于提高势能面的精度会有改善.

图8 置换对称不变多项式势能面与测试数据的差值等高图Fig.8 Contour plots of the difference between the permutation-invariant polynomial method and the test data

3.2 多中心展开构建H3势能面

3.2.1 坐标的选取

为了描述H + H2反应体系, 选取H2为中心原子,通过两个键长(R1, R2)和一个键角(θ)表示, 坐标选取如图1所示.

3.2.2 计算方法

3.2.2.1 训练集数据的选取

采用DMBE2001势能面25作为测试集, 取R1, R2∈ [0.05 nm, 0.5 nm]均匀100 个点; 均匀取θ ∈[0°, 180°]30个点, 得到各数据点的能量值.

3.2.2.2 分区原则

在H + H2→ H2+ H的最小反应路径上取7个(R1, R2)(单位: nm), 作为七个中心点, 计算训练集中的数据点(R1, R2)与七个中心的距离, 依据最近及次近距离将数据集分成7个区域, 当R1= R2时, 存在两个次小数据点与各中心点间距值, 将此点纳入相应的两个分区, 拟合数据的分布与误差统计如表3所示.

3.2.2.3 边界处理

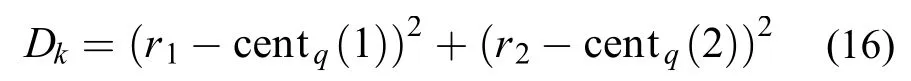
合并拟合分区, 将各数据点根据公式(18)计算相应的能量值: centq为此数据点所在数据域的中心点, q = 1, 2, 3, , 7. wk为分区能量在总能量中的权重, 表示如下:

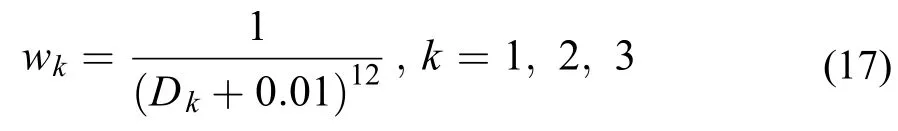
表3 拟合数据分布及误差统计Table3 Distribution of the fitting data and the error statistics

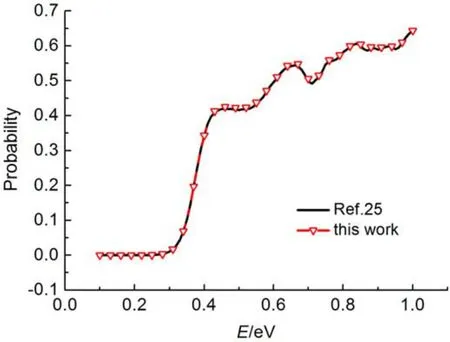
图9 多中心分区法计算准经典轨线的结果Fig.9 Results of quasiclassical trajectory by “multi-center partition” method

当此数据点仅存在于两个分区时, w3= 0, vfitj3= 0, vfitjk表示处在第j个分区时，第k次近中心点对总势能面的贡献. 则多中心分区能量(单位为cm–1)为:

3.3 多中心展开构建H3势能面

采用多中心分区拟合后, 构建势能面的准经典轨迹计算结果与文献完全一致, 如图9所示. 由图9可以看出, 多中心分区拟合后, 构建势能面与原势能面回归性很好, 相比全域拟合(图7), 精度进一步提高, 无论是在低能区域, 还是在高能区域, 都与文献值完全吻合.

4 结 论

构建了H3体系的LEPS势能面, 采用三种不同势能函数, 构建了H3分子势能面, 为多中心分区方法确定了最佳拟合函数形式, 应用准经典轨迹法验证了势能面的合理性, 最后采用多中心分区拟合, 构建了H3分子势能面. 研究结果表明:

(1) LEPS势能面参数少, 除Si参数需调节确定,其余参数都可通过从头计算得到, 势能函数形式简单, 使用方便, 在定性计算中可以广泛使用, 但不适宜描述高精度反应势能面, 动力学验证误差较大.

(2) 比较了三种不同的势能函数形式. 训练集采用了213200个构型的能量信息, 截断能为40000 cm–1,数据量大, 能域宽. PIP方法统计误差最小, 动力学信息最吻合, 可以用来描述H3分子势能面的能量特征.

(3) 拟合势能面的精度与表达式展开的项数、数据集的数据量大小密切相关. 多中心分区之后,每一区域数据集变少, 改变了数据集和拟合参数的相对比, 可以降低拟合表达式展开项的要求, 同时有效改善拟合精度. 从计算结果可以看出: 多中心分区拟合法相比全域拟合, 势能面回归性很好, 无论是在低能区域, 还是在高能区域, 都与文献值吻合很好.

(1)Sun, Z. F.; Gao, Z.; Wu, X. K.; Tang, G. Q.; Zhou, X. G.; Liu, S. L. Acta Phys. -Chim. Sin. 2015, 31, 829. [孙中发, 高 治, 吴向坤, 唐国强, 周晓国, 刘世林. 物理化学学报, 2015, 31, 829.] doi: 10.3866/PKU.WHXB201503041

(2)Li, W.; Qu, J. Y.; Zhao, X. S. Acta Phys. -Chim. Sin. 2003, 19 (8), 751. [李 巍, 屈军艳, 赵新生. 物理化学学报, 2003, 19 (8), 751.] doi: 10.3866/PKU.WHXB20030816

(3)Le, H. A.; Frankcombe, T. J.; Collins, M. A. J. Phys. Chem. A 2010, 114 (40), 10783. doi: 10.1021/jp1060182

(4)Ramazani, S.; Frankcombe, T. J.; Andersson, S.; Collins, M. A. J. Chem. Phys. 2009, 130 (24), 244302. doi: 10.1063/1.3156805

(5)Moyano, G. E.; Jones, S. A.; Collins, M. A. J. Chem. Phys. 2006, 124 (12), 124318. doi: 10.1063/1.2181571

(6)Moyano, G. E.; Collins, M. A. Theor. Chem. Acc. 2005, 113 (4), 225. doi: 10.1007/s00214-004-0626-8

(7)Evenhuis, C. R.; Collins, M. A.; Lin, X.; Zhang, O. H. Amer. Chem. Soc. 2004, 227, 259.

(8)Moyano, G. E.; Pearson, D.; Collins, M. A. J. Chem. Phys. 2004, 121 (24), 12396. doi: 10.1063/1.1810479

(9)Castillo, J. F.; Aoiz, F. J.; Bañares, L.; Collins, M. A. J. Phys. Chem. A 2004, 108 (32), 6611. doi: 10.1021/jp048366b

(10)Moyano, G. E.; Collins, M. A. J. Chem. Phys. 2003, 119 (11), 5510. doi: 10.1063/1.1599339

(11)Fuller, R. O.; Bettens, R. P. A.; Collins, M. A. J. Chem. Phys. 2001, 114 (24), 10711. doi: 10.1063/1.1377602

(12)Song, K.; Collins, M. A. Chem. Phys. Lett. 2001, 335 (5), 481.

(13)Collins, M. A.; Zhang, D. H. J. Chem. Phys. 1999, 111 (22), 9924. doi: 10.1063/1.480344

(14)Bettens, R. P. A.; Hansen, T. A.; Collins, M. A. J. Chem. Phys. 1999, 111 (14), 6322. doi: 10.1063/1.479937

(15)Jordan, M. J. T.; Collins, M. A. J. Chem. Phys. 1996, 104 (12), 4600. doi: 10.1063/1.471207

(16)Li, H.; Le, R. R. J. J. Chem. Phys. 2006, 125 (4), 044307. doi: 10.1063/1.2212933

(17)Li, A. Y.; Xie, D. Q. J. Chem. Phys. 2010, 133 (14), 144306. doi: 10.1063/1.3490642

(18)Wu, T.; Manthe, U. J. Chem. Phys. 2003, 119 (1), 14. doi: 10.1063/1.1577328

(19)Ishida, T.; Schatz, G. C. J. Chem. Phys. 1997, 107 (9), 3558. doi: 10.1063/1.474695

(20)Takata, T.; Taketsugu, T.; Hirao, K.; Gordon, M. S. J. Chem. Phys. 1998, 109 (11), 4281. doi: 10.1063/1.477032

(21)Crespos, C.; Collins, M. A. J. Chem. Phys. 2004, 120 (5), 2392. doi: 10.1063/1.1637337

(22)Wang, M.; Sun, X.; Bian, W.; Cai, Z. J. Chem. Phys. 2006, 124 (23), 234311. doi: 10.1063/1.2203610

(23)Dawes, R.; Thompson, D. L.; Guo, Y.; Wagner, A. F.; Minkoff, M. J. Chem. Phys. 2007, 126 (18), 184108. doi: 10.1063/1.2730798

(24)Corchado, J. C.; Bravo, J. L.; Espinosa-Garcia, J. J. Chem. Phys. 2009, 130 (18), 184314. doi: 10.1063/1.3132223

(25)Varandas, A. J. C.; Brown, F. B.; Mead, C. A. J. Chem. Phys. 1987, 86, 6258. doi: 10.1063/1.452463

(26)Bowman, J. M.; Czako, G.; Fu, B. Phys. Chem. Chem. Phys. 2011, 13 (18), 8094. doi: 10.1039/c0cp02722g

(27)Pukrittayakamee, A.; Malshe, M.; Hagan, M.; Raff, L. M.; Narulkar, R.; Bukkapatnum, S.; Komanduri, R. J. Chem. Phys. 2009, 130 (13), 134101. doi: 10.1063/1.3095491

(28)Le, H. M.; Raff, L. M. J. Phys. Chem. A 2010, 114 (1), 45. doi: 10.1021/jp907507z

(29)Sumpter, B. G.; Noid, D. W. Chem. Phys. Lett. 1992, 192 (5), 455.

(30)Blank, T. B.; Brown, S. D.; Calhoun, A. W.; Doren, D. J. J. Chem. Phys. 1995, 103 (10), 4129. doi: 10.1063/1.469597

(31)Connor, J. N. L. Comput. Phys. Commun. 1979, 17, 117. doi: 10.1016/0010-4655(79)90075-4

(32)Eyring, H.; Polanyi, M. Phys. Chem. Abt. B 1931, 12, 279.

(33)Sato, S. J. Chem. Phys. 1955, 23 (12), 2465.

(34)Aguado, A.; Paniagua, M. J. Chem. Phys. 1992, 96 (2), 1265. doi: 10.1063/1.462163

Application of the Multi-Center Partition Method to Construct the Potential Energy Surface of H3

DAI Wei1,2CHEN Liu-Yang2ZHENG Li-Min2YANG Ming-Hui2,*
(1School of Physics and Mechanical & Electrical Engineering, Hubei University of Education, Wuhan 430205, P. R. China;2Wuhan Institute of Physics and Mathematics, Chinese Academy of Sciences, Wuhan 430071, P. R. China)

The potential energy surface plays an important role in studying molecular reaction dynamics. In this work, a new method, namely the “multi-center partition” method, is proposed to construct the potential energy surface of H3. The optimized function is first determined by comparing the London-Eyring-Polanyi-Sato (LEPS) potential, the many-body expansion potential, and the permutation-invariant polynomial potential. This comparison shows that the permutation-invariant polynomial fitting proposed by Bowman is the most efficient method for describing the topology of the H3system. The quasi-classical trajectory method is used to analyze the rationality of those potential energy surfaces. By combining the multi-center partition method with the permutation-invariant polynomial method, the accuracy of the H3molecular potential energy surface is greatly improved and could possibly be used in the fitting of potential energy surfaces in other systems.

Potential energy surface fitting; Quasi-classical trajectory method; Multi-center partition

O641.3

10.3866/PKU.WHXB201509143

Received: July 6, 2015; Revised: September 14, 2015; Published on Web: September 14, 2015.

*Corresponding author. Email: yangmh@wipm.ac.cn; Tel: +86-27-87197783.

This project was supported by the China Scholarship Council (201408420174), Science and Technology Research Program of the Education Department, Hubei Province, China (Q20133005), and Natural Science Foundation of Hubei Province, China (2014CFB428, 2015CFB502).

国家留学基金委项目(201408420174), 湖北省教育厅科学技术项目(Q20133005)和湖北省自然科学基金(2014CFB428, 2015CFB502)资助

©Editorial office of Acta Physico-Chimica Sinica