注重智慧引领，提升操作实效

【摘 要】随着课程改革的不断深入，“动手操作”已成为学生数学学习的重要方式。然而，在教学实践中，由于教师往往只关注动手操作的结果而忽视其它要素，致使动手操作活动“形神分离”。基于此，教师需要智慧引领，帮助学生正确认识操作工具，深入理解操作原理，充分利用操作成果，实现操作从低效到高效的转变;操作中促进学生对数学活动有本质地理解，积累数学活动经验，提升思维品质，扩大动手操作活动效益。

【关键词】缺失;引领;操作;效益;归位

随着课程改革的不断深入，“动手操作”已成为学生数学学习的重要方式，它能使抽象的数学知识形象化，深化学生对知识的理解和掌握，积累数学活动经验。然而，在教学实践中，由于学生对操作素材认识不透、对操作原理理解不深、对操作成果预见不足等原因，导致课堂中存在着操作“形”“神”分离，“动手”“动脑”脱节等低效操作的现象。如何提高“动手操作”的有效性，提升教学效益，还需教师智慧地引领学生对操作工具、原理、成果等有正确的认识和把握，实现操作从低效到高效的转变。

一、理清“是什么”——正确认识操作工具

操作工具是学生从事操作活动的载体，教材中对操作工具的使用介绍具有普适性、一般化的特点，教师要引领学生正确地认识操作工具究竟“是什么”，并有所“创新”地运用，激活学生更多的智力思索，促进对知识的理解与掌握。

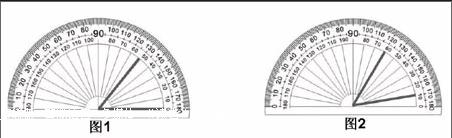
如用量角器量角时，教材中呈现的方法是“两重合，再看数”，即量角器的中心点与角的顶点重合，“0刻度线”与角的一条边重合，再看角的另一条边指向的刻度数。在具体教学时，教师们都将这一方法视为“法宝”教给学生，要求严格按“规范”操作。诚然，这样的方法便于学生记忆，但学生在用量角器量角时易出现以下两类错误：其一是外圈刻度与内圈刻度错位选取，比如110°的角学生易误读成70°;其二是学生在两个整十刻度间易错位反向读取，比如135°的角学生易错位读成145°。对操作工具缺乏正确认识是学生错误的重要原因之一。

用量角器量角的本质不在于角的边指向的刻度数，而在于要度量的角中包含了多少个1°的角。教学时，教师应先引导学生认识量角器，让学生在量角器上找出“角”来，比划出这个角的顶点和两条边，加深学生对量角器上若干隐存“角”的认可和理解。如图1角中包含了50个1°的小角，这个角就是50°。

图2角的一条边并没有与“0刻度线”重合，但这个角中也包含了50个1°的小角，也是50°。在引领学生充分认识量角器的基础上，再将要量的角与量角器上的角重合，逐渐使学生理解“量角就是把要量的角重叠在量角器上”的操作本质。从而也能理解“两重合，再看数”是较为便捷的量角方法，但它的实质不是看角的另一条边所指向的刻度。

二、认识“为什么”——深入理解操作原理

操作活动不仅要有目标的引领，还应深入理解操作原理，使操作活动更显灵活与灵动;相反，失去原理支撑，操作活动会显得呆板与教条，将学生异化为机械的操作工，丧失数学活动的意义与价值。教学中，教师不但要使学生掌握怎样操作，还应深入理解为什么这样操作，使操作动手更动脑，知其然更知其所以然。

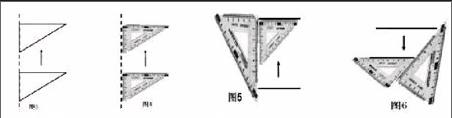
笔者在听课时曾经遇到过这样的尴尬现象，一位教师在教学“平行线的画法”时，学生自学课本后按照教材中的方法模仿画一组平行线，但坐在我身旁的学生一动不动。当我轻声询问他为什么不按老师的要求操作时，他回答自己只有一副三角尺，忘记了带直尺。其中的潜台词是：要画平行线必须像教材中那样有一把直尺和一个三角尺，否则就无法操作了。为什么会出现这样的现象？对“一重、二靠、三移、四画”的步骤多数学生只知其“形”不知其“神”，对“为什么这样画能得到一组平行线？”缺乏应有的理解，缺乏对数学活动的本质认识。由于对操作原理理解不透，导致操作僵化，机械模仿，不能灵活处置。为此，我们可以增加“静态找平行”到“动态找平行”教学环节，使学生感悟到“平移可以得到平行线”这一数学思想，为下面的操作行为提供智力支撑。

教师可以提问：图3中的三角形是怎样平移的？你能找出平移前后两个三角形中的平行线吗？图4中的三角尺又是怎样平移的？你能找出其中的平行线吗？从而使学生感悟到“平移可以得到平行线”的数学思想，进而理解“一画、二靠、三移、四画”的操作依据，实现操作从机械模仿向思维引领的转变，学生也能理解并掌握图5、图6等操作方法。这样的动手操作才会是有源之水，有本之木，学生也才能更为自主与灵活地从事操作活动。

三、明晰“还有什么”——扩大运用操作成果

在操作目标的引领下，经过智力地思索，经历操作的过程，操作成果也展现在眼前。而此时需打破思维定势，明晰教材中出示的“显性成果”，适时呈现教材中未出示的“隐性成果”，引导学生对操作成果充分地利用，放大动手操作活动的效益，发展学生思维，提升思维品质。

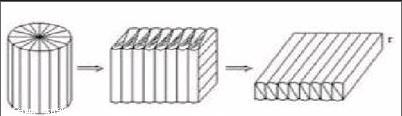
如：“圆柱的体积”教学时，引导学生运用转化的方法把圆柱底面平均分成若干个小扇形，切开后拼成一个近似的长方体。通过拼成的长方体与原来圆柱体之间的关系逐步推导出“圆柱的体积=底面积×高”。此时对新知的探索也就此结束，留给学生的是“自古华山一条道”——要求圆柱的体积必须要先知道圆柱的底面积和高。但长方体的任何一个面都可以作为底面，与底面垂直的棱作为高。此时，可以引导学生换个视角思考，把长方体的前面作为底面，将其“倒”下来，就会发现长方体的底面积其实是圆柱侧面积的一半，高就是圆柱的底面半径，进而可以推导圆柱体积的另外一种计算方法，圆柱的体积=侧面积的一半×底面半径。教师还可以引导学生继续沟通两种计算方法之间的联系：V圆柱=πr2×h=π×r×r×h=π×r×h×r=2πr×h÷2×r=S侧÷2×r。这时，学生一定能体验到数学方法的千变万化，感悟到数学真好玩，动手操作的活动效益得以充分彰显。

提高动手操作的有效性是实现有效教学的关键之一，是积累数学活动经验的重要途径。苏霍姆林斯基说过：“儿童的智慧在他的手指尖上”，在课堂教学实践中须提升学生动手操作的智慧，实现智慧地动手操作。

【作者简介】

曹志国，男，本科学历，小学高级教师，扬州市中青年教学骨干，现担任江苏省宝应县桃园小学副校长。从教17年来，一直致力于小学数学教学研究，曾多次获省、市、县教学类竞赛一等奖，二十余篇论文发表于省级以上教育类期刊。

（作者单位：江苏省宝应县桃园小学）