两个自由度Duffing系统的分岔及混沌分析
2015-12-06曹振邦
曹振邦,乐 源
(西南交通大学力学与工程学院,成都 610031)
近年来耦合非线性系统在物理、化学、生物、机电设备系统等许多科学领域中都有广泛的应用,引起了众多研究者的关注。在这些系统中最具有代表性的,也是研究最深入的要数Duffing振荡器系统[1-4],而具有耦合项是这类系统区别于其他系统的本质特征,因而众多的国内外学者也对其理论推导、数值模拟等方面进行了大量的研究。Pastor[5]研究了具有对称耦合项的van der Pol系统,分析了不动点的结构及系统通向混沌的道路。Stagliano[6]研究了一个具有不可约频率的加性耦合项的两自由度Duffing系统,观察到在一定的参数条件下系统会出现倍周期分岔。进而,Koziowski[7]分析了这类系统的全局分岔现象。目前关于耦合项对系统响应及混沌运动的研究还不够充分,因此有必要对其做进一步研究。
1 系统模型描述
船舶在海洋中的航行HE航空航天设备的运行[8]可用如下数学模型来描述:
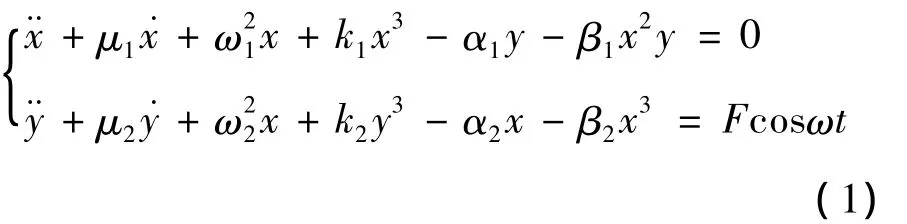
式中:圆点表示对时间的导数;μ1和μ2为阻尼系数;ω1和ω2为线性固有频率;k1和k2为非线性刚度系数;α1,α2,β1和 β2表征了两个单自由度系统的耦合程度;Fcosωt为系统所受的周期性外力。
2 系统稳定性分析
无论是对稳定性分析或对数值模拟分析来说,把二阶微分方程(1)化成一个自治一阶微分方程(2)会更方便一些:

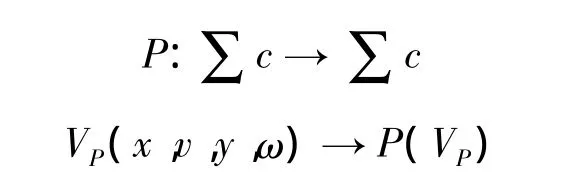
由于稳定性分析比较简单,这部分的分析在本文下一节一并给出结论。
3 系统的分岔及混沌分析
非线性耦合系统的分岔研究对于考察系统与混沌运动的关系具有重要的意义,而分岔图是研究系统拓扑结构随参数变化的良好工具。因此,本文利用系统中较易调整的参数,即外加周期力的强度F和外加周期力的频率ω作为控制参数研究耦合系统的分岔过程,从而分析其通向混沌的道路。参数取值为:μ1=0.2;μ2=0.2;ω1=0.2;ω2=0.4;k1=0.3;k2=0.5;α1=0.4;α2=0.2;β1=0.12;β2=0.08;ω =1.0。迭代初值取(-0.3,0.5,0.6,-0.8,0),控制参数 F取值范围F∈(0,1.3),采用四节龙格库塔方法进行数值模拟,结果见图1~8。

图1 F变化过程中x的分岔图
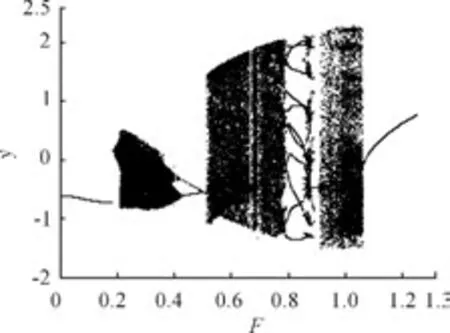
图2 F变化过程中y的分岔图
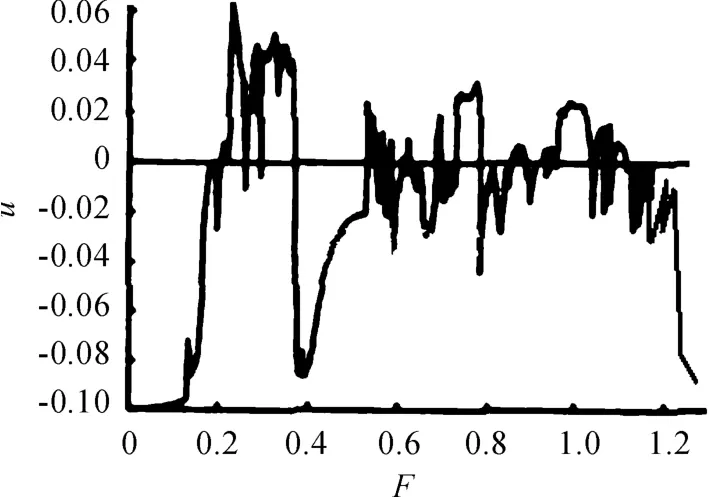
图3 F变化过程中的最大Lyapunov指数图
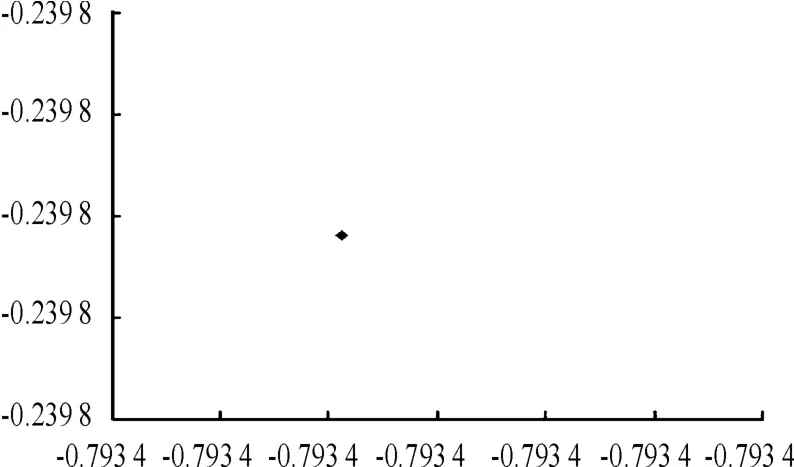
图4 F=0.1时的Poincaré映射图
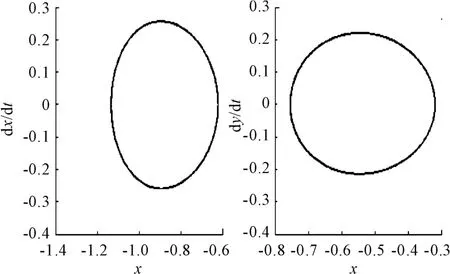
图5 F=0.1时的相图

图6 F=0.3时的Poincare映射图
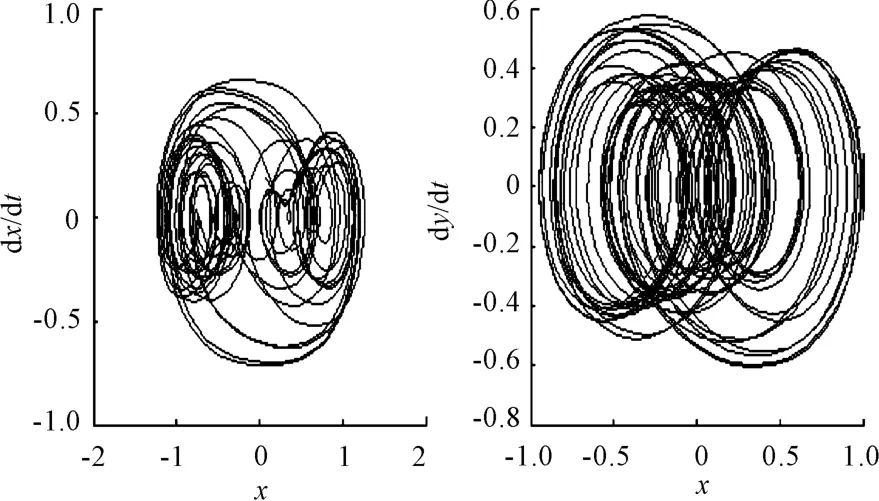
图7 F=0.3时的相图
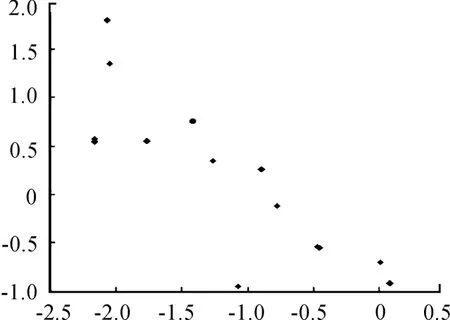
图8 F=0.85时的Poincaré映射图
通过比较图1和图2可知:在F变化过程中x的分岔图和y的分岔图在结构上是相似的,这在定性分析上是必然的。由于最大Lyapunov指数中μ大于0说明系统处于混沌状态,小于0处于非混沌状态,故结合图3的最大Lyapunov指数图就可以看出分岔图是完全正确的。由图4和图5可以看出:在很小时(本文选的点F为0.1)系统做的是周期1运动,当F达到0.21时系统突然达到混沌状态,而这种混沌状态并不能说是由周期1引发的,只能说在F=0.21点处时周期1运动和混沌是共存的,故该点处的系统的行为是比较复杂的。而在这里通过图6和图7可以简单说明混沌是一种很复杂的混乱状态。当达到0.43时系统出现倒分岔现象,又进入到周期1运动继而进入混沌状态,然后系统由周期6通过周期倍化分岔变为周期12运动(见图1和图8),然后进入混沌区,最后回归周期1运动。
4 结束语
通过对周期性驱动力作用下两个自由度的Duffing系统分岔及混沌分析可以发现,由于耦合项的存在使得系统在随控制参数变化的过程中其运动形态非常复杂,可以看出系统经由周期倍化分岔可以进入混沌状态,而系统由周期1直接突发进入混沌状态这更体现出其复杂性。
[1]冷永刚,赖志慧,范胜波,等.二维Duffing振子的大参数随机共振及微弱信号检测研究[J].物理学报,2012(23):71-80.
[2]刘海波,吴德伟,金伟,等.Duffing振子微弱信号检测方法研究[J].物理学报,2013(5):42-47.
[3]刘海波,吴德伟,戴传金,等.基于Duffing振子的弱正弦信号检测方法研究[J].电子学报,2013(1):8-12.
[4]杨红英,叶昊,王桂增,等.Duffing振子的Lyapunov指数与Floquet指数研究[J].仪器仪表学报,2008(5):927-932.
[5]Pastor L,Perez-Garcia V M,Encinas-Sanz F,et al.Orderd and chaotic behavior of two coupled Vander Por Oscillators[J].phys Rev E,1933,48(1):171-182.
[6]Stagliano J J,Wersinger J M,Slamminka E E.Doubling bifurcation of destroyed tori[J].Physica D,1996,92(3):164-177.
[7]Koziowski J,Pralitz U,Lauterborn W.Bifurcation analysis of two couple periodically driven Duffing oscillator[J].Phys Rev E,1995,51(3):1861-1867.
[8]陈予恕.非线性振动系统的分岔理论和混沌理论[M].北京:高等教育出版社,1993:180-198.
